Disclosing the Complexity of Nonlinear Ship Rolling and Duffing Oscillators by a Signum Function

Chein-Shan Liu

1 Introduction

A cubic nonlinear oscillator described by the Duffing equation has the following form:

wherexis the displacement,γ is a damping constant,F0and ω are respectively the amplitude and excitation frequency of a harmonic loading,andis the frequency of natural oscillation of the corresponding linear system.

The Duffing equation has been a major subject of intensive study over the last few decades as one of innocent examples of nonlinear dynamical system exhibiting chaotic behavior,and which lends a typical chaotic system with a period doubling route to chaos.The study of nonlinear oscillators is of great importance not only in all areas of physics but also in engineering and other disciplines,since most phenomena in our world are nonlinear and are described by nonlinear equations.Recently,a considerable attention has been directed towards the semi-analytical solutions for nonlinear oscillators.There are many computational methods that have been developed for solving the periodic and sub/super-harmonic solutions of the nonlinear oscillators,for example,the harmonic balance method[Donescu1,Virgin and Wu(1996);Wu,Sun and Lim(2006),Liu,Thomas,Dowell,Attar and Hall(2006)],the variational iteration method[He(1999);Ozis and Yildirim(2007)],the homotopy perturbation method[He(2000);Shou(2009)],the parameter-expanding method[Koroglu and Ozis(2011)],theexp-function method[He and Abdou(2007)],and differential transform method[Chu and Lo(2011)].Recently,Dai,Schnoor and Atluri(2012)have applied a simple collocation method to reveal the complex subharmonic behavior of the Duffing oscillator,and Liu(2012)proposed a Liegroup adaptive method to solve the optimal control problem of nonlinear Duffing oscillator.

The chaotic behavior of ship rolling motion in beam sea has been studied by Thompson(1997),of which a typical equation to explore the instability of ship capsize is the following quadratic nonlinear oscillator:

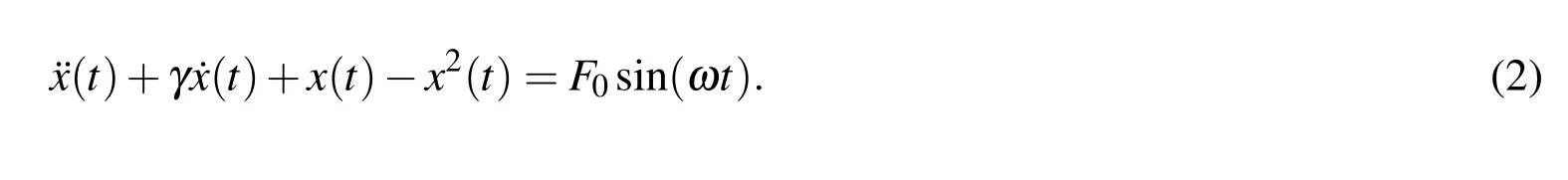
In the studies of ship motion the analysis of large amplitude nonlinear rolling motion is important to understand the capsize dynamics.

The analyses of Eqs.(1)and(2)have been performed to obtain approximate solutions by using various methods,like multiple scale method,perturbation method,harmonic balance method,the Bogoulibov Mitropolsky asymptotic method.The numeric safe basins,the Melnikov method,the Lyapunov exponents and the Lyapunov direct method were used to determine the conditions of stability and the occurrence of chaotic motion.The analytic methods used to predict chaos[Szemplinska-Stupnicka(1995);Litak and Borowiec(2006)]are also developed by using an observation of period doubling,and Melnikov’s method based on the phenomenon of homoclinic intersection.But there are still many problems that the existent methods cannot exhaust the complicated beahvior of nonlinear dynamical systems.

Figure 1:There are four Lie-symmetries for the nonlinear dynamical system,wheregroups for the nonlinear dynamical system,where X=

2 A nonlinear augmented system formulation

To facilitate the formulation we write the above equations as a system of first-order ordinary differential equations(ODEs):

which is ann-dimensional ODEs system.

As that done by Liu(2001),for Eq.(3)we can define a unit orientation vector:

First,upon using Eqs.(3)and(4)the length kxk is governed by

Then,using Eqs.(3)-(5)we can derive

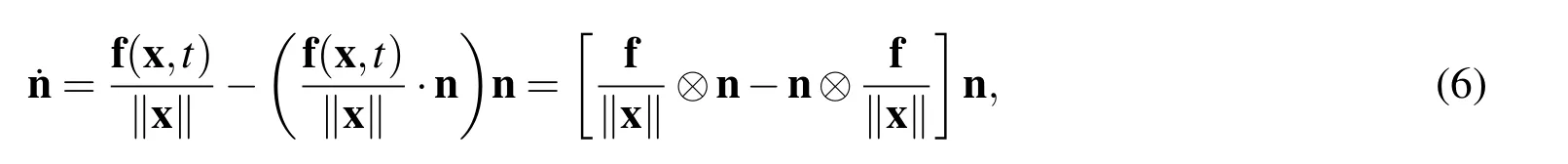
whereu⊗ydenotes the dyadic operation ofuandy,i.e.,(u⊗y)z=y·zu.By the definition of

and from Eqs.(4)-(6),we can derive

and at the same time Eq.(5)can be written as

Then,Eqs.(7)and(8)can be put together as

Furthermore,in terms of

and in terms of the symmetric and skew-symmetric matrices:

we can write Eq.(9)as a Lie-type ODEs:

We can find three structures about Eq.(9):

whereg:=diag(In,−1)is the metric tensor of the Minkowski space Mn+1with a signature(n,1),andGis the Lie-group generated fromB[Liu(2001)].Recently,Liu(2013a)has developed a Lie-group algorithm based on the Lie-symmetryGL(n,R)by dropping out the first and the third terms in the right-hand side of Eq.(7).Moreover,Liu(2013b)has developed a Lie-group algorithm based on the Lie-symmetryDSO(n)by Eq.(7).In Fig.1 we show the relations of those Lie-group formulations to Eq.(3).The present formulation by using the full Lie-symmetry ofSOo(n,1)is more delicated,as to be shown below.

3 A signum function

In order to develop a numerical scheme from Eq.(9),we suppose that the coefficient matrix is constant with the pair

being constant,which can be obtained by taking the values offandxat a suitable mid-point of¯t∈[0,t],wheret≤handhis a small time stepsize.

From Eqs.(9)and(17)we thus need to solve a constant linear system:

At the same time,from the above equations we can derive the following ODEs forz,wandy:

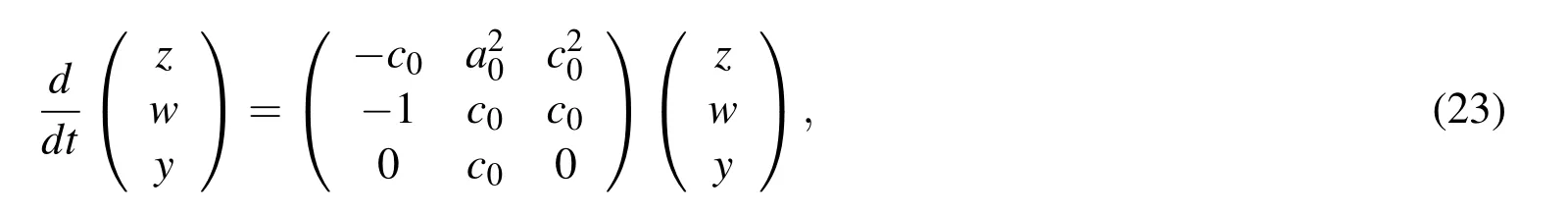
wherea0=kak.Fortunately,the original(n+1)-dimensional problem in Eq.(18)can be reduced to a three-dimensional problem in the above.

For the special case withc0=0 we can derive

where Ω =kak,z0=a·x0andw0=b·x0.For this case kxk is a constant.

Here we give a detailed derivation of the solutions for(z,w,y)withc06=0.Depending on the signum function of

there exist two different types solutions of(z,w,y)of Eq.(23).Instead of sign(a20−2c20),we will use Sign for a shorthand.

From the first-order ODEs in Eq.(23)we have

Depending on the value ofa20−2c20,yhas two different types of solutions.

(A)For the first case witha20−2c20<0,i.e.,Sign=−1,we have

When(z,w,y)are obtained we can insert them into Eq.(21)and integrate the resultant equation to obtain the solution ofx(t).The solutions are written out directly.

Figure 2:A schematic plot of the area of Sign=+1,Sign=-1,sign(c0)=+1,and sign(c0)=−1 in the plane.

(A)For the case witha20−2c20<0(Sign=−1),inserting Eq.(30)forz,wandyinto Eq.(21)and integrating the resultant equation we can obtain

4 Numerical algorithm:GPS2

From the above solutions ofx(t)we can derive the new algorithm.In order to distinct the present method from the group-preserving scheme(GPS)developed by Liu(2001),we may call the new algorithm to be the second GPS,denoted by GPS2,which is summarized as follows.

(i)Give an initial value ofx0at an initial timet=t0and a time stepsizeh.

(ii)Fork=0,1,...,we repeat the following computations to a specified terminal timet=tf:

Figure 3:For the Duffing oscillator under a harmonic loading,showing(a)the signum function and(b)the length.

In Eq.(40)there are sin(Ωkh)and cos(Ωkh),while that in Eq.(41)there are sinh(Ωkh)and cosh(Ωkh).The most dynamical systems fall into the first class with Sign=+1.However,for a chaotic system the situation is quite different,where both equations(40)and(41)are needed in the computation.

5 The barcode and the set A1−

It is significant that in Eq.(25)we have derived a signum function,which is abbreviated as Sign for saving notation,to demand the algorithm into two classes in Eqs.(40)and(41).Without having the factor 2 beforef·xin Eq.(25)one has

where θ is the intersection angle betweenxandf;hence,it makes no sense to say its signum function,because it is always non-negative.

On the contrast,by Eq.(25)we have

which might be+1 or−1,depending on the intersection angle θ betweenxandf.When θ is in the range of−π/2<θ <π/2 or 3π/4<θ <5π/4,the value of Sign is Sign=−1.As a remark given below Eq.(23),here we can classify the behavior of the nonlinear dynamical system in a three-dimensional subspace(f,x,kxk)with a trio(Sign,sign(c0),kxk).Thus we can observe the time-varying values of Sign and plot them as a barcode with alternative values of Sign being+1 and-1.It is known that a barcode is an optical machine-readable representation of data relating to the object to which it is attached.A main feature of the barcode is the intervened black lines and white lines with varying spacings and widths.Barcode is ubiquitously used in the identification and classification of products.Here we will use the barcode to identify the property of nonlinear oscillators in Eqs.(1)and(2).

Definition 1:The barcode is a time-varying function of Sign defined in a time interval.

Let us give a schematic plot in Fig.2,and as shown there we have two dis-connected sets of kfk2kxk2−2(f·x)2<0:

by noting that(x,f)=(0,0)is deleted.Then we can identify five time-varying sets:

While B+and B−are connected,A1−and A2−are dis-connected.We may call A1−the first set of dis-connectivity and A2−the second set of dis-connectivity,respectively.Clearly,the first set of dis-connectivity is a subset of B+and the second set of dis-connectivity is a subset of B−,i.e.,

We can prove the following theorems,which can help us understand the complex structure of a barcode.

Theorem 1:If Eq.(3)satisfies

Proof:Under the first assumption the case in Eq.(45)is impossible because it contradicts tof(x(t0),t0)·x(t0)>0.Then under the condition of Sign=sign(kfk2kxk2−2(f·x)2)=−1,it is always

which is in the set A1−by Eq.(46).Because the two sets A1−and A2−are disconnected,and from the first set A1−to the second set A2−it must be Sign=sign(kfk2kxk2−2(f·x)2)=+1 on some time interval,which contradicts to the second assumption in Eq.(52).Then using Eqs.(8)and(53)we have

which means that the length grows with time.Thus,Eq.(52)is proven.?

Theorem 2:If Eq.(3)satisfies

Proof:Under the first assumption the case in Eq.(44)is impossible because it contradicts tof(x(t0),t0)·x(t0)<0.Then under the condition of Sign=sign(kfk2kxk2−2(f·x)2)=−1,it is always

which is in the set A−2by Eq.(47).By a similar argument and then using Eqs.(8)and(56)we have

which means that the length decreases with time.Thus,Eq.(55)is proven.?

We note that the length as governed by Eq.(8)has the following property:

The above two theorems also hold if we replace A1−and A2−by the sets B+and B−,but they are un-interesting,because for an oscillatory system the value of sign(c0)always changes its sign between+1 and-1.

For a chaotic system the value of Sign is not always+1 or−1.In order to demonstrate the use of the barcode,let us investigate the Duffing oscillator(1)under the following parameters:γ=0.3,α =−1,β =1,F0=0.32,ω =1.2.In all computations the initial conditions are set to be(x(0),˙x(0))=(0,0),unless specifying otherwise.By using the algorithm GPS2 in Section 4 to solve the Duffing equation the time stepsize ish=0.01.We analyze the signum function and the length as shown in Fig.3 within a time interval oft∈[200,220],where the transient part int∈[0,200)is not plotted for clear.

As shown in Fig.3(a)by solid line the values of Sign are varying from−1 to+1 and then to−1,and then Sign will return to+1 again;otherwise,as shown in Theorem 1 the system will respond unstably,causing the displacement tend to infinity,which by definition is not a chaotic system.In order to compare the values of sign(c0)with the values of Sign we plot them in Fig.3(a)with dashed and solid line,respectively,where we make a slight shift of the dashed line downward for clear.On the other hand,for a distinction to A2−,the first set of dis-connectivity A1−is filled by solid black points.

Theorem 3:If a state is in the set A1−⊂B+,before it leaves the set B+to B−,the set A1−changes to A+.

Proof:It follows from the first equation in Eq.(51)and the dis-connectivity of A1−and A2−.?

Theorem 4:If a state is in the set A2−⊂B−,before it leaves the set B−to B+,the set A2−changes to A+.

Proof:It follows from the second equation in Eq.(51)and the dis-connectivity of A1−and A2−.?

Before sign(c0)changes from+1 to−1,for example from pointf1to pointf2in Fig.2,the Sign must jump from−1 to+1.The two jumping behaviors described in Theorems 3 and 4 render a quite complex structure of the barcode as shown in Fig.3(a).More barcodes are to be shown below,which can be seen very complex.From Fig.3(a)we can observe the following interesting phenomena:(i)The first set of dis-connectivity A1−is a subset of sign(c0)=+1,and the second set of dis-connectivity A2−is a subset of sign(c0)=−1.(ii)In a time interval of Sign=−1,the state is either in the first set of dis-connectivity A1−or in the second set of dis-connectivity A2−,which is due to the dis-connectivity of A1−and A2−.(iii)From one in first set of dis-connectivity A1−to another first set of dis-connectivity A1−there must accompany a jump from Sign=−1to Sign=+1.This also holds for the second set of dis-connectivity A2−.(iv)From one in first set of dis-connectivity A1−to one in second set of dis-connectivity A2−,or vice-versa,there must accompany a jump from Sign=−1 to Sign=+1.For some cases this jumping event only happens at one time point[an example will be given in Fig.11(b)].(v)Before sign(c0)jumps from+1 to−1 as remarked in Fig.3(a)by the symbols+and−(i.e.,the length is decreased),and if Sign is in the state of−1,then Sign will jump from−1 to+1 as remarked in Fig.3(a)by the symbols−and+.The proof of(v)is obvious by viewing Fig.2 and that the first set of Sign=−1 cannot directly jump to the second set of Sign=−1.Whenf1goes tof2,the Sign changes from−1 to+1.

Moreover,according to the numerical algorithm of GPS2 we can prove the following result.

Theorem 5:If Eq.(3)satisfies

wheret0is a small finite time.

Proof:Under the above condition of Sign=+1,the algorithm in Eq.(40)is used.Because|sin(Ωkh)|≤ 1 and|cos(Ωkh)|≤ 1,the algorithm does not bring the state ofxto be unbounded.Indeed,the Lie-group transformation fromxktoxk+1is a compact subgroup ofSOo(n,1),whose action is bounded.?

Theorems 1 and 2 reflect two extremal cases with the state always being Sign=−1,which is either unstable or tending to zero.Thus for a regular system it should go to the state Sign=+1 after a certain timet0as shown in Theorem 5.However,a chaotic system is frequently switching between these two states of Sign=+1 and Sign=−1.This is the reason that the barcode of a chaotic system is quite complex.In the next section we will demonstrate the importance of the first set of dis-connectivity A1−for Duffing equation(1)and the ship rolling equation(2).

6 Results and discussions

In this section we apply the GPS2 to solve Eqs.(2)and(1),and investigate their behaviors by using the barcode and its fi rst set of dis-connectivity A1−.

(A)Ship rolling equation:

(i)For Eq.(2)with γ=0.1(we fix it,unless specifying otherwise),under a fixedF0=0.2,and with two different ω =0.76 and ω =0.6,we plot the phase portraits of(x,y)=(x,˙x)in Fig.4(a),where we can observe two type behaviors:The escape one with ω=0.76 whose Sign function is plotted in Fig.4(b)with an unstable behavior as specified by Theorem 1.Here we can only calculate the solution up tot=12 sec although we use a very small time stepsizeh=0.0005.The periodic one(in steady state)with ω=0.6,whose Sign function is plotted in Fig.4(c)with stable behavior as specified by Theorem 5.The Sign is returned to Sign=+1 after 25 sec and until 200 sec it keeps Sign=+1 unchanged.

(ii)In order to further test the escape and chaotic behavior of Eq.(2),we plot the percentage of the state in the first set of dis-connectivity A1−up to 500 sec for two fixed values,F0=0.2 in Fig.5(a)andF0=0.15 in Fig.5(b),with respect to the excitation frequency ω in the range of 0.1≤ω≤1.The curves are fi tted with black points and connected by dashed lines and in the escape state there exist no black points.The GPS2 has a mechanism to identify the"instability"of solution by checking the value of Ωkhin Eq.(41).Because Ωkhappears in cosh(Ωkh)and sinh(Ωkh),when Ωkh≥ 20 the algorithm will blow up and we terminate the computation,although the time does not reach tot=500 sec,of which the resultant state is classified as"escape"in the parameter space of ω.Thompson,Bishop and Leung(1987)have employedx>20 to be an escape criterion.Here we employ the criterion of Ωkh≥20,basing on the numerical algorithm.For the case ofF0=0.2,after ω>0.6 there are all escape states,and another one indicated in Fig.5(a)by a piece of dashed line.After the escape state there exists a thin layer within which the motion is chaotic.In the percentage curve of A−1there appears many peaks,such as those marked by the numbers 0.2935,0.334 and 0.5635 in Fig.5(a),and under these parameter values of ω we find respectively,1/3 subharmoic,1/2 subharmoic and periodic motion as shown in the inset.In the chaotic state,the percentage of A1−is very low,smaller than 1%,for the ship rolling equation(2).We remind that in the hyperplane(x,f)as shown in Fig.2,A1−might have the maximal percentage 25%.

(iii)In order to show the chaotic behavior of Eq.(2),we compare two steady state behaviors in Fig.6(a)with the same ω=0.17 but with two slightly different values ofF0=0.2414 andF0=0.2415,which correspond respectively to 1/4 subharmonic and chaotic motion.The corresponding barcodes as compared in Fig.6(b)forF0=0.2415,and Fig.6(c)forF0=0.2414 are slightly different.Although,the difference ofF0is only 0.0001,but the resultant behaviors are very different.This indicates that Eq.(2)is a chaotic system under certain parameter values,which is sensitive to the parameter value.

(iv)In Figs.7(a)and 7(b)we fix γ=0.1 and γ=0.05 by plotting the distribution of escape states in the parameter space of(ω,F0)∈ [0,1]×[0,0.4],where the escape states are marked by black points.For the purpose of comparison the following Melnikov curve[Thompson(1989)]is plotted in Fig.7:

F0>FMis a necessary condition for the appearance of chaos,but it is not a sufficient condition.In Fig.8 we plot the escape time which is the terminal time whenΩkhused in in Eq.(41)is arrived to 20.After that the algorithm blows up.There have several cusps and adjunct them the state of chaos appears.For example the above case withF0=0.2415 is near to a cusp of escape.In the largest cusp region there is a fractal structure as shown in the inset of Fig.7(a),which is plotted in the range of(ω,F0)∈ [0.8,1]×[0.06,0.16].(v)With in the large cusp,Thompson,Rainey and Soliman(1990)have analyzed the bifurcation behavior with a fixed value ω =0.85 and varyingF0∈[0.107,0.109].However,in that range we cannot detect any special structure by using the new theory.In Fig.9 with ω=0.85 being fixed,we plot the bifurcation diagram by using the percentage curve of A1−with respect toF0in the range ofF0∈[0.06,0.108].

Figure 4:For a quadratic oscillator under a harmonic loading,(a)escape and chaotic orbit,and the signum functions for(b)escape motion and(c)periodic motion.

Figure 5:For quadratic oscillators under harmonic loadings,showing escape and chaotic regions for two amplitudes of force.The inset shows subharmonic motions.

Figure 6:For quadratic oscillators,(a)showing subharmonic and chaotic motions with slightly different amplitudes of force,and(b)and(c)the corresponding barcodes.

Figure 7:For quadratic oscillators under harmonic loadings,showing escape regions for two damping constants.

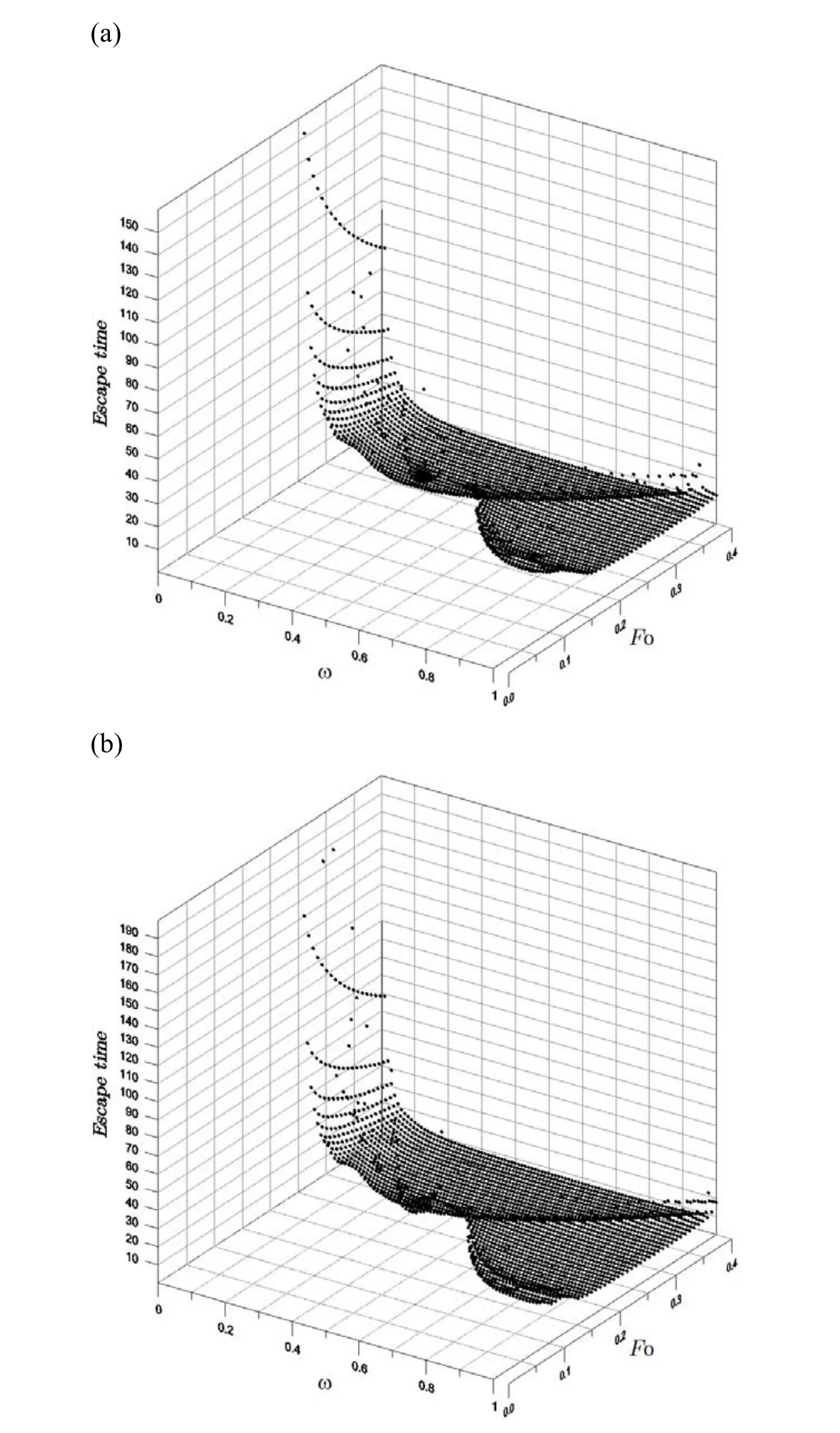
Figure 8:For quadratic oscillators under harmonic loadings,showing escape times for two damping constants:(a)γ=0.1,and(b)γ=0.05.

It is interesting that after a sequence of period-doubling bifurcation showing as a devil staircase in the figure there are states of escape and chaos.

Figure 9:For quadratic oscillators under fixed ω=0.85 and varying amplitudes of loading,showing a bifurcation diagram with the staircase structure.

(B)Duffing equation:

(i)For the Duffing Eq.(1)we fix the parameters as those given in the computation of Fig.3.Under the same parameters of γ=0.3,α = −1,β =1,ω =1.2,we plot the curves of the percentages of sign(c0)=+1(i.e.,B+)and A1−with respect toF0fromF0=0.22 toF0=0.4 in Fig.10.The time is up to 250 sec and withh=0.005 sec used in the GPS2.As expected the curve in Fig.10(a)gives no much useful information about the motion types,whose percentages are near 50%.However,in the percentage curve of A1−in Fig.10(b)there appears many peaks,such as those marked by the numbers 0.267,0.288 and 0.301,0.356 and 0.359,and under these parameter values of ω we find respectively,a smaller 1/3 subharmoic(Fig.11),1/4 subharmoic(Fig.12),chaotic(Fig.13),a larger 1/3 subharmoic(Fig.14)and a larger 1/5 subharmoic(Fig.15).The last two subharmonic motions are within the subharmonic window inside the chaotic range.The range of 1/3 subharmoic is ω ∈[0.356,0.359),while the range of 1/5 subharmoic is ω ∈[0.359,0.38).After ω=0.38 the Duffing system returns to the chaotic motion.For this case the Melnikov theory gives a quite conservative estimation of chaos withF0≥0.25276.But we find that the chaos is happened afterF0≥0.301.

Figure 10:For the Duffing oscillator under different amplitudes of harmonic loading,showing the percentage of(a)the signum function c0,and(b)the first set of dis-connectivity.

Figure 11:For the Duffing oscillator under F0=0.267,showing(a)the steady orbit of 1/3 subharmonic motion,and(b)the barcode.

Figure 12:For the Duffing oscillator under F0=0.288,showing(a)the steady orbit of 1/4 subharmonic motion,and(b)the barcode.

Figure 13:For the Duffing oscillator under F0=0.301,showing(a)the steady orbit of chaotic motion,and(b)the barcode.

Figure 14:For the Duffing oscillator under F0=0.356,showing(a)1/3 subharmonic motion inside a window of chaotic range,and(b)the barcode.

Figure 15:For the Duffing oscillator under F0=0.359,showing(a)1/5 subharmonic motion inside a window of chaotic range,and(b)the barcode.

Figure 16:For the Duffing oscillator under F0=0.2895,comparing the results of(a)RK4,and(b)GPS2.RK4 gives an incorrect 1/4 subharmonic motion.

(ii)For the value ofF0=0.2895 which is near to the starting value of chaosF0=0.301,it leads to a higher subharmoic motion through period doubling route.However,the fourth-order Runge-Kutta method with a time stepsizeh=0.005 gives an incorrect 1/4 subharmonic motion as shown in Fig.16(a),while the GPS2 can reveal a higher subharmoic motion in Fig.16(b).The steady state motions are shown in a time interval oft∈[500,2000].

AfterF0=0.2676 the Duffing equation comes to a period-doubling range until the entrance to a chaotic state atF0=0.301.Then we come to a narrow range of 1/3 subharmoic motion in the range ofF0∈[0.356,0.359),and then a 1/5 subharmonic motion in the range ofF0∈[0.359,0.38].In summary,we have found two ranges ofF0∈[0.301,0.356)]andF0>0.38 for the chaotic motions of the nonlinear Duffing oscillator.

7 Conclusions

In this paper the nonlinear differential equations system was converted into an augmented quasi-linear dynamical system in the Minkowski space,with the coefficient matrix being a Lie-form withB∈so(n,1).Based on the Lie-symmetry of the underlying new system,we have derived two types closed-form Lie-groupG∈SOo(n,1)solutions,of which the numerical scheme to preserve the Lie-group properties was developed.A signum function of sign(kfk2kxk2−2(f·x)2)was introduced.Then we have announced a very important concept of the first set of dis-connectivity in the hyper-plane(x,f),whose variation with respect to the parameter of nonlinear dynamical systems as shown by the Duffing equation and the ship rolling equation reveals special structures.In view of Eqs.(43)and(59),the set of A1−:={sign(cosθ)=+1 and sign(cos2θ)=+1}plays a dominant role for disclosing the complexity of nolinear dynamical systems.The barcode can be used to detect the appearance of chaotic motion,of which the peak in the curve of the percentage to stay in the set of A1−is an important criterion to forecast the subharmonic motions and chaos.One of the major contribution of this paper was that the proposal of the bifurcation diagram obtained by plotting the percentage of the first set of dis-connectivity A1−with respect to the amplitude of external loading,which leads to a finer structure of the devil staircase for the quadratic oscillator,and the cascade of subharmonic motions to chaotic motions for the Duffing oscillator.Hence,one has a practical and convenient tool to assess the complex behavior of nonlinear oscillators.

Acknowledgement:Taiwan’s National Science Council project NSC-100-2221-E-002-165-MY3 and the 2011 Outstanding Research Award,granted to the author,are highly appreciated.Acknowledges that the author has been promoted to be a Lifetime Distinguished Professor of National Taiwan University,since 2013.

Chu,H.P.;Lo,C.Y.(2011):Application of the differential transform method for solving periodic solutions of strongly non-linear oscillators.CMES:Computer Modeling in Engineering and Sciences,vol.77,pp.161-172.

Dai,H.H.;Schnoor,M.;Atluri,S.N.(2012):A Simple collocation scheme for obtaining the periodic solutions of the Duffing equation,and its equivalence to the high dimensional harmonic balance method:subharmonic oscillations.CMES:Computer Modeling in Engineering and Sciences,vol.84,pp.459-498.

Donescu,P.;Virgin,L.N.;Wu,J.J.(1996):Periodic solutions of an unsymmetric oscillator including a comprehensive study of their stability characteristics.Journal of Sound and Vibration,vol.192,pp.959-976.

He,J.H.(1999):Variational iteration method–a kind of non-linear analytic technique:some examples.International Journal of Non-Linear Mechanics,vol.34,pp.699-708.

He,J.H.(2000):A coupling method of a homotopy technique and a perturbation technique for non-linear problems.International Journal of Non-Linear Mechanics,vol.35,pp.37-43.

He,J.H.,Abdou,A.(2007):New periodic solutions for nonlinear evolution equations using exp-function method.Chaos Soliton&Fractals,vol.34,pp.1421-1429.

Koroglu,C.;Ozis,T.(2011):Applications of parameter-expanding method to nonlinear oscillators in which the restoring force is inversely proportional to the dependent variable or in form of rational function of dependent variable.CMES:Computer Modeling in Engineering and Sciences,vol.75,pp.223-234.

Litak,G.;Borowiec,M.(2006):Oscillators with asymmetric single and double well potentials:transition to chaos revisited.Acta Mechanica,vol.184,pp.47-59.

Liu,C.-S.(2001):Cone of non-linear dynamical system and group preserving schemes.International Journal of Non-Linear Mechanics,vol.36,pp.1047-1068.

Liu,C.-S.(2012):The optimal control problem of nonlinear Duffing oscillator solved by the Lie-group adaptive method.CMES:Computer Modeling in Engineering and Sciences,vol.86,pp.171-197.

Liu,C.-S.(2013a):A method of Lie-symmetryGL(n,R)for solving non-linear dynamical systems.International Journal of Non-Linear Mechanics,vol.52,pp.85-95.

Liu,C.-S.(2013b):A Lie-groupDSO(n)method for nonlinear dynamical systems.Applied Mathematics Letters,vol.26,pp.710-717.

Liu,L.;Thomas,J.P.;Dowell,E.H.;Attar,P.;Hall,K.C.(2006):A comparison of classical and high dimension harmonic balance approaches for a Duffing oscillator.Journal of Computational Physics,vol.215,pp.298-320.

Ozis,T.;Yildirim,A.(2007):A study of nonlinear oscillators withu1/3force by He’s variational iteration method.Journal of Sound and Vibration,vol.306,pp.372-376.

Shou,D.H.(2009):The homotopy perturbation method for nonlinear oscillators.Computational Mathematics and Applications,vol.58,pp.2456-2459.

Szemplinska-Stupnicka,W.(1995):The analytical predictive criteria for chaos and escape in nonlinear oscillator:a survey.Nonlinear Dynamics,vol.7,pp.129-147.

Thompson,J.M.T.(1989):Chaotic phenomena triggering the escape from a potential well.Proceeding of the Royal Society of London A,vol.421,pp.195-225.

Thompson,J.M.T.(1997):Designing against capsize in beam seas:recent advance and new insights.Applied Mechanical Review,vol.50,pp.307-325.

Thompson,J.M.T.;Bishop,S.R.;Leung,L.M.(1987):Fractal basis and chaotic bifurcations prior to escape from a potential well.Physical Letters,vol.121,pp.116-120.

Thompson,J.M.T.;Rainey,R.C.T.;Soliman,M.S.(1990):Ship stability criteria based on chaotic transients from incursive fractals.Philosophy Transactions of the Royal Society London A,vol.332,pp.149-167.

Wu,B.S.;Sun,W.P.;Lim,C.W.(2006):An analytical approximate technique for a class of strongly non-linear oscillators.International Journal of Non-Linear Mechanics,vol.41,pp.766-774.