广义帕雷托分布在波浪极值推算中的应用＊

韩树宗，刘 昆

（中国海洋大学海洋环境学院，山东 青岛266100）

海洋中的波浪是海水运动形式之一，它的产生是外力、重力与海水表面张力共同作用的结果。引起海水波动的外力因素有很多，比如风、大气压力的变化、天体的引潮力、海底地震以及人为引起的船体的运动等。

海岸和近海工程建筑物处于严酷的海洋环境下，在着手进行海上建筑物的规划和设计之前，必须得到相应海区的可靠波浪资料，掌握其统计特性。为了掌握工程海域的波浪状况，最可靠的方法是进行现场观测。1960年代以来，为了适应建设的需要，国家海洋局在沿海各地陆续建立了一些水文气象观测站、台，进行系统的观测以累积资料。但是对于像石油平台之类的远离岸边的工程建筑，海浪资料的获取往往非常困难。因此，运用卫星资料进行海浪的数值模拟一直是海浪研究的重要方面，也是海洋预报和分析的主要手段和工具。

海浪的数值模拟发展到20世纪末已达到比较成熟的阶段，由荷兰科学家开发的SWAN（Simulating Waves Nearshore）模式具有较好的海浪模拟精度。近些年国外较为先进的SWAN海浪模式已被广泛应用于中国海域的风浪模拟。

帕雷托分布是以意大利经济学家维弗雷多·帕雷托命名的，起初应用于经济领域，后来渐渐发现其在气象和水文极值参数分析中也有很好的适用性。广义帕雷托分布（GPD）是由Pickands在1975年首次引入的，后来很多学者做了进一步研究，该分布被广泛应用于极值分析领域。国内研究中，张香云等[1]利用GPD分析了洛杉矶降雨量数据，发现GPD能较好的拟合数据分布的尾部，且随着样本容量增加，估计效果越来越好；江志红等[2]利用GPD拟合了我国东部地区的极端降雨量，并且与广义极值分布（GEV）相比较，GPD拟合效果更好，且计算更为方便；程炳岩等[3]引进GPD模拟重庆极端降水事件，借助于L－矩估计方法，GPD基本不受原始序列样本量的影响，具有更好精度的实用性和稳定性。国外研究者们则把GPD的应用范围扩展到海洋水文极值参数的研究中，Bermudez等[4]对GPD的参数估计做了细致的研究，运用了最大似然估计（ML）、概率权重矩法（PWM）和矩法（MOM）分别进行了估计分析；Kevin等[5]利用GPD对北海北部海域百年一遇有效波高进行研究，分析了不同临界值下百年一遇极值的变化；Philip等[6]运用GPD估计了GOMOS海浪数据百年一遇有效波高，对GPD参数估计引入了波向，讨论了考虑波向的分布模型和不考虑波向的模型之间的稳定性问题，认为考虑方向的模型稳定性更好。

对于波浪重现期极值参数的推算工作，大家所熟知的是年最大值统计法（AM），即每年取1个最大值组成样本的方法，年最大值统计法是广义极值分布（GEV）的1个重要前提。部分历时序列统计法（PDS）则是取合适的临界值，每年可取多个超过临界值的值组成样本。GPD属于运用部分历时序列统计法的1种分布，对于1年多次取样法，目前在波浪重现期极值参数的推算当中的研究较少。本文在前人基础上继续深入研究，CCMP风场资料（1988年1月～2010年12月）共23年的风场资料对中国海的海浪场进行模拟，并借助GPD模型对重现期极值参数进行推算。

1 资料简介

1.1 风场资料

CCMP（Cross－Calibrated Multi－Platform）数据是结合了SSM/I、 TMI、AMSR－E、 QuikSCAT 和ADEOS－II几种资料通过交叉校验和同化得到的，其时间分辨率为6h，空间分辨率为0.25（°）×0.25（°），时间范围从1987年7月～2011年6月，空间范围为0.125°E～359.875°E，78.375°S～78.375°N。CCMP风场资料有着良好的精度和时空分辨率。

本文选取了CCMP风场资料（1988年1月～2010年12月）共23年的风场资料作为SWAN模式的驱动场，进行海浪场的数值模拟。

1.2 实测海浪资料

实测海浪资料采用日本气象厅（JMA）22001号海洋观测浮标资料，22001号浮标坐标为126°20′E，28°10′N。浮标提供了有效波高（1990—2000年）和海表面10m高风速（1980—2000年）资料。观测间隔为3h，当风速大于18m/s时观测时间间隔变为1h。

图1 模拟计算范围网格图Fig.1 Grid map of calculation range

2 模拟方法和资料验证

2.1 模拟方法

SWAN模式属于第三代浅海海浪数值模式，由荷兰Delft大学土木工程系开发并维护。从第一个公开发布的版本SWAN30.51开始，不断进行改进和扩充，性能不断提高，功能也逐渐增强。本文利用SWAN模式对中国海1988年1月～2010年12月的海浪场进行模拟。

模拟海域计算范围：4°N～42°N，105°E～136°E。驱动风场数据插值到5（′）×5（′）的网格上，模型计算网格分辨率为4（′）×4（′），计算步长为1h，每24h输出一次结果，计算时间为1988年1月1日00：00时～2010年12月31日00：00时。

2.2 资料验证

郑崇伟[7]利用月 CCMP（Cross－Calibrated Multi－Platform）风场资料，对中国海近22年的海表风场特征进行分析，结果显示，中国海大部分海域的海表风速呈显著性逐年线性递增。李燕[8]利用SWAN模式对黄渤海域波浪场进行计算，经系数订正后，预报准确率达70%以上，有一定的预报能力。梅婵娟等[9]利用第三代海浪数值模式 WAVEWATCH和SWAN模式，分别对黄海区域进行了理想模拟计算和实际浪场的模拟计算，发现SWAN模式模拟结果较 WAVEWATCH模式好，只是在高风速的模拟情况下，SWAN模式模拟结果偏大，而WAVEWATCH模式模拟结果偏小。

图2 模拟计算范围地形图Fig.2 Topographic map of calculation range

为了更加直观的比较SWAN模式模拟的结果与浮标实测结果之间的差异，本文在计算中提取了2000年的驱动风场风速值和有效波高模拟值，与22001号浮标（126°20′E，28°10′N）实测资料相对应，作出散布图。并且进行了误差分析，计算了偏差（Bias）、平均绝对误差（MAE）、均方根误差（RMSE）和相关系数（CC）。

式中：xi代表浮标观测数据；yi代表SWAN计算结果；分别代表观测数据和计算结果的平均值；n为样本总量。

图3 实测风速与CCMP混合风场风速散布图Fig.3 Comparison of wind speed between observed data and CCMP data

图4 实测有效波高与CCMP混合风场有效波高散布图Fig.4 Comparison of significant wave height between observed data and CCMP data

由图3可见，驱动风场和22001号浮标观测的风速相一致，统计上存在0.54的正偏差，说明驱动风场风速稍大于实测风速，相关系数为0.77，通过了99%的信度检验，均方根误差为2.55m/s，平均绝对误差为1.95m/s，卫星风场精度较好。由图4可见，模拟有效波高和22001号浮标观测的有效波高相一致，统计上存在0.01的负偏差，说明模拟有效波高稍大于实测有效波高，相关系数为0.75，通过了99%的信度检验，均方根误差为0.71m，平均绝对误差为0.48m，模拟的海浪场可用。

图5 计算有效波高与实测有效波高极大值验证图Fig.5 Comparison of extreme significant wave height between observed data and calculated data

本文所关心的是波浪的极值参数，因此波浪极值参数模拟的准确度就至关重要。鉴于22001号浮标有较为完整的1990—2000年波高资料，根据浮标资料分别补充验证了年最大值，第二大值和第三大值（见图5）。图5中点表示浮标实测有效波高，线表示模拟计算有效波高。其中，1988年计算波高普遍较小，低于4m，最大值、第二大值和第三大值均取为4m。从图5中可以看出，模拟结果极值有效波高在大部分年份偏低，这与SWAN模式在极端风速下运算不稳定有关，但整体差异不算很大。本文采用此次SWAN模拟的波浪场数据作为样本，进行波浪极值参数推算新方法的尝试，还是可行的。

3 极值估计方法

目前国内外常用的极值估计方法总的来说可以分为两类：一类是经验型的，如皮尔逊III型曲线法等，一类是以极值分部理论为基础的，如耿贝尔（Gumbel）曲线法、威布尔（Weibull）曲线法等。皮尔逊III型曲线法虽然有较大的实用性，但是其缺乏严格的概率论理论依据，在海洋资料的分析中，最常用的是耿贝尔分布和威布尔分布。耿贝尔分布和威布尔分布都属于广义极值分布（GEV）的特殊形式。

GEV的分布形式函数为：

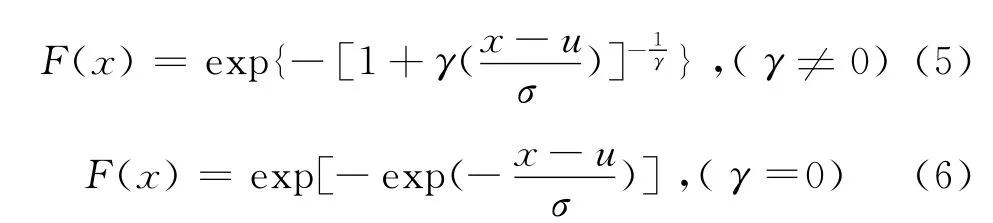
式中：γ成为形状参数或尾部指数；σ成为尺度参数；u为阈值。当γ＝0时，GEV简化为Tippett I型分布，即Gumbel分布；当γ＞0时，为Tippett II型分布；放γ＜0时，则为Tippett III型分布，即 Weibull分布。

前面提到广义极值分布（GEV）的1个重要前提就是年最大值统计法。对于一些年份，可能出现年最大值和年次大值差距很大的情况，也可能出现1年有多个差不多的极大值的情况，如果采取每年抽取1个最大值的方法，其实并不符合实际。因此，这种年最大值统计法，会舍去很多有用的信息，形成的样本量小，不能充分利用分析资料。而广义帕雷托分布（GPD）属于运用部分历时序列统计法的1种分布，每年可取多个超过临界值的值组成样本，一定程度上解决了上述方法的缺陷。

GPD的分布形式函数为：

式中：γ成为形状参数或尾部指数；σ成为尺度参数；u为阈值。对于给定的重现期T（年），可证明[3]重现期极值xT如下：

式中：λ成为年交叉率[10]，即极值超过给定阈值的个数。对于给定阈值情况下的年交叉率，一般采用多年平均的年交叉率即可。

式中：n为超过给定阈值的总样本量；A为资料的总年数。在以上的理论基础上，本文采用L－矩参数估计方法求得GPD对应的参数，进而对重现期极值进行推算。

3.1 L－矩法参数估计

参数估计方法中比较常用的有矩法（MOM）、概率权重矩法（PWM）和最大似然估计（ML）。根据段忠东等[11]对不同极值概率分布参数的研究，虽然最大似然估计具有较高的精确度和稳定性，但在多数情况下，矩法和最大似然估计法都不能获得参数估计的解析表达，需要数值求解强非线性方程组。L－矩法起源于“概率权重矩（PWM）”，是概率权重矩的线性组合，他的一个显著优点是可以得到参数的显示表达式，从而使得参数估计变的简便，L－矩法的参数估计精度较高，估计值的稳定性也比较强。

首先将样本由大到小排序（x1≤x2≤ …xn），根据PWM的定义[12]，随即变量x的第r阶概率加权矩为：

线性组合后的样本L－矩前四阶计算式如下：

根据文献[13－14]，GPD的L－矩估计式为：

根据样本L－矩和GPD的L－矩估计式，可以推算出GPD的参数估计式如下：

4 GPD方法应用实验

4.1 不同阈值下的GPD模型参数估计及其效果检验

在以上的理论参考下，对不同阈值情况下GPD模型的拟合结果进行检验分析。鉴于前面22001号浮标计算结果验证良好，故选取22001号浮标（126°20′E，28°10′N）点作为实验点，对该点处SWAN计算得出的23年的有效波高数据进行分析，分析结果见表1。选取科尔莫格洛夫检验统计量（K－S）、相关系数和均方根误差3个指标对拟合见过进行检验。

由表1可见，GPD模型的模拟结果较好，K－S统计量很小，拟合的分布函数和经验分布函数之间的相关系数都在0.9以上，均方根误差几乎为零。从表1还可以看出：随着阈值的增大，样本量不断下降，一直到阈值为5.5m时，样本量为25，仍大于年最大值法的样本量，利用有限的数据获取更丰富的信息；随着阈值的增大，拟合的分布函数和经验分布函数之间的相关系数不断减小，这与样本量的减小是息息相关的，这说明样本量越大，GPD模型的拟合结果越好。

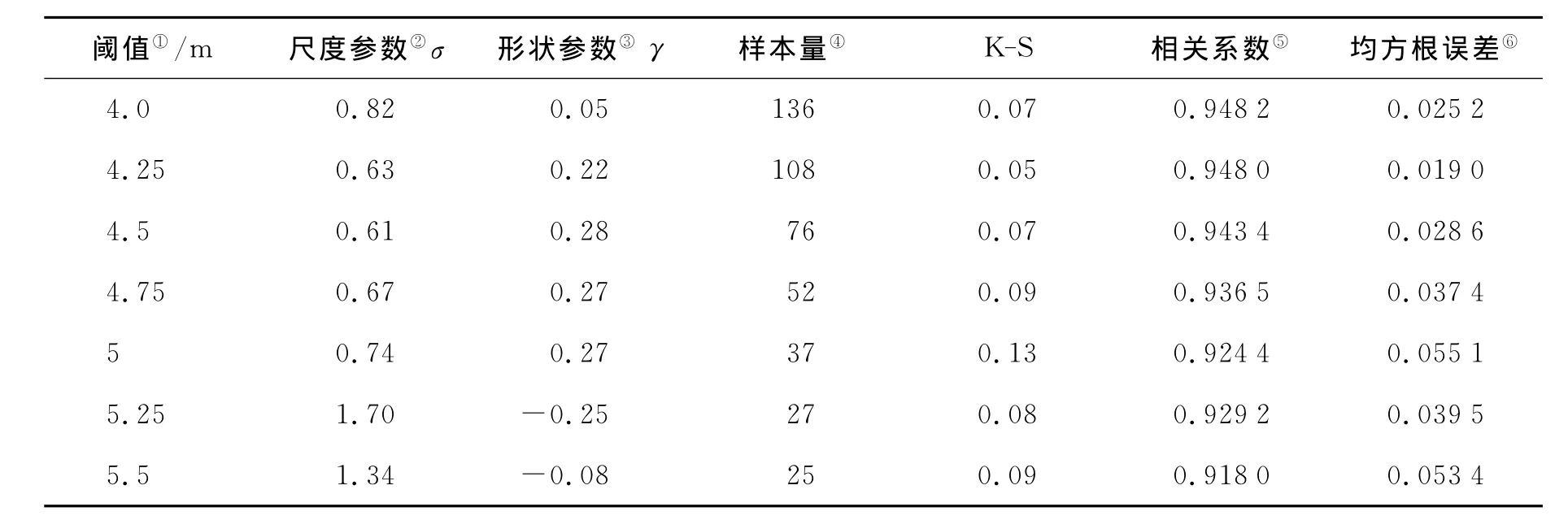
表1 不同阈值下的GPD模型参数估计及其效果检验Table 1 The test of effect for GPD model under different thresholds

4.2 选定阈值（4m）的情况下，对GPD模型和GEV模型的模拟结果进行比较

选定阈值为4m，GPD模型运用部分历时序列统计法提取样本。GEV模型采用年最大值统计法提取样本。分别用GPD分布和GEV分布对拟合累积频率曲线并进行检验，结果如下：

表2 两种模型拟合结果检验Table 2 Comparison of GPD and GEV models

图6 实验点累积概率的GPD模拟曲线Fig.6 The simulated curve of GPD for cumulative probability

从以上结果可以看出，GPD模型的模拟结果在各方面都好于GEV模型，检验指标上也表现良好，主要原因在于GPD模型更充分的利用了有限的资料，取得了更丰富的样本，曲线拟合效果更好，在海浪极值参数的推算上有一定应用价值。4.3选定阈值（4m）的情况下，对浮标附近区域尺度参数σ和百年一遇有效波高的求解分析

图7 实验点累积概率的GEV模拟曲线Fig.7 The simulated curve of GEV for cumulative probability

尺度参数σ是标准差线性函数，σ的大小标识着极值有效波高的稳定性，σ越大表明极值有效波高之间的差别也越大越不稳定。下面选定浮标附近区域（27°N～29°N，126°E～127°E）为例，对区域内σ的分布进行简单的分析。由图可以看出，在选定区域内浮标西部为尺度参数高值区，浮标东部为尺度参数低值区。说明浮标西部区域极大波高值较不稳定，浮标东部区域相反，极大波高值较稳定。

从浮标附近区域百年一遇有效波高空间分布来看，浮标西南部百年一遇有效波高较大，最大值超过15m，浮标东北部百年一遇有效波高较小，多在10m以下。大浪的成长需要足够的风区，浮标所在的海域近似可以看成由中国大陆、朝鲜半岛、日本群岛、琉球群岛和台湾岛所包围。从有效波高的分布来看，岸界附近的海域有效波高较小，远离岸界的海域有效波高较大，同时有利于极值波高的出现。因此图中浮标左侧波高大于右侧。

图8 22001号浮标附近区域σ分布Fig.8 Spatial distribution ofσnear NO.22001buoy

5 结论

图9 22001号浮标附近区域百年一遇有效波高分布（m）Fig.9 Spatial distribution of significant wave height of 100－year return level near NO.22001buoy

随着经济的发展，海洋石油的开采越来越受到国际的关注，海洋石油平台的选址不仅要考虑油气资源分布、水深、地质、气象等条件，工程海域的海洋环境状况不容忽视。浮标东北部海域百年一遇有效波高较小且极大波高值较稳定，海洋环境状况明显优于浮标西部海域。在实际应用中，GPD分布模型有着较强的应用价值。

本文利用CCMP卫星风场资料模拟了中国海域1988—2010年共23年的波浪场，并利用日本气象厅22001号海洋观测浮标资料进行了风场和有效波高验证；采用广义帕雷托分布（GPD）模型对22001号浮标点计算有效波高极值进行拟合，分析了GPD模型在不同阈值下的估计结果并进行效果检验，比较了GPD模型和GEV模型的优劣；计算了浮标附近海域尺度参数σ和百年一遇有效波高分布，得出如下结论：

（1）在不同阈值的情况下，样本量越大，GPD模型的拟合结果越好。

（2）GEV每年只取一个极大值，得到的样本量小，资料信息较少，GPD模型采用部分历时序列统计法采样，增大了样本容量，拟合结果在相关程度和效果检验方面都表现出色。从前人的研究成果和本文的验证结果来看，GPD模型不仅在降雨、洪水等方面有较好的应用，在海洋水文极值参数的估计中也有很好的应用价值。

（3）GPD模型的尺度参数σ的大小可以反映极值的稳定性，尺度参数σ和百年一遇有效波高可以在一定程度上表征出海洋环境恶劣状况，它们的空间分布特征对海洋石油平台工程的选址有一定参考价值。

[1]张香云，赵旭.广义Pareto模型统计推断及其应用 [J].数理统计与管理，2011，30（6）：989－995.

[2]江志红，丁裕国，朱莲芳，等.利用广义帕雷托分布拟合中国东部日极端降水的试验 [J].高原气象，2006，28（3）：573－580.

[3]程炳岩，丁裕国，张金铃，等.广义帕雷托分布在重庆暴雨强降水研究中的应用 [J].高原气象，2008，27（5）：1004－1009.

[4]Pierre Ribereau，Philippe Naveau，Armelle Guillou.A note of caution when interpreting parameters of the distribution of excesses[J].Advances in Water Resources，2011，34：1215－1221.

[5]Kevin Ewans，Philip Jonathan.The effect of directionality on Northern North Sea extreme wave design criteria [J].Journal of Offshore Mechanics and Arctic Engineering，2008，130：1－8.

[6]Philip Jonathan，Kevin Ewans.The effect of directionality on extreme wave design criteria [J].Ocean Engineering，2007，34：1977－1994.

[7]郑崇伟.基于CCMP风场的近22年中国海海表风场特征分析[J].气象与减灾研究，2011，34（3）：41－46.

[8]李燕，薄兆海.SWAN模式对黄渤海海域浪高的模拟能力试验[J].海洋预报，2005，22（3）：75－82.

[9]梅婵娟，赵栋梁，史剑.两种海浪模式对中国黄海海域浪高模拟能力的比较 [J].海洋预报，2008，25（2）：92－98.

[10]郭军，任国玉，李明财.环渤海地区极端降水事件概率分布特征[J].气候与环境研究，2010，15（4）：425－432.

[11]段忠东，周道成.极值概率分布参数估计方法的比较研究 [J].哈尔滨工业大学学报，2004，36（12）：1605－1609.

[12]丁裕国，刘吉峰，张耀存.基于概率加权估计的中国极端气温时空分布模拟试验 [J].大气科学，2004，28（5）：771－782.

[13]Hosking J R M，Wallis J R.Parameter and quantile estimation for the generalized Pareto distribution[J].Technometries，1987，29：339－349.

[14]Zhai Panmao，Sun Anjing，Ren Fumin，et al.Changes of climate extremes in China[J].Climatic Change，1999，42：203－218.

[15]P deZeaBermudeza，SamuelKotzb.Parameter estimationofthegeneralizedParetodistribution[J].Journal of Statistical Planning and Inference，2010，140：1353－1373.