基于灰关联层次分析法的大学生体质健康评价
2014-04-17杜晶
杜 晶
(四川理工学院,四川 自贡 643000)
0 引言
近年来,影响大学生的体质健康水平的原因很多,对大学生体质健康的评价问题将为如何提高体质健康水平有现实指导意义.目前,学生体质健康状况已经纳入对学校整体工作的评价体系中,大学生的体质健康测试成为高等院校必须完成的任务。各高校每年都会对在校大学生做体质健康测试,将测试的结果反馈教育部,并及时公布。体质测试主要包括身体形态、身体机能、运动能力等方面。具体测试项目有:身高、体重、肺活量、立定跳远、握力、坐位体前屈、台阶试验等。
大学生体质健康问题越来越受到各界的关注,研究者已分析了影响大学生体质健康的影响因素,如杨进[1]研究了武汉音乐学院大学生体质健康评价模型与干预对策,对影响因素进行了阐述和聚类分析,并采用主观赋权的直线式加权法平均法对体质健康。本文通过灰关联层次分析法[2-3]对高校学生体质健康进行评价,客观反映学生个体间的差异,并达到科学、准确的评价效果。
1 层次分析法
本文要确定各项指标对学生体质评分的权重,但是在不同评价指标下对体质健康影响的重要性不同,这就要求对各项指标下的得分进行线性加权。下面建立层次分析模型[4],求解各项指标的权重。现行的《大学生体质健康标准》对测试项目的分类[5]为:(1)身体形态(身高/标准体重);(2)身体机能(肺活量体重指数、台阶实验);(3)运动能力(立定跳远、握力体重系数)。本体质健康模型的指标因素共五个,分别为:身高/标准体重、肺活量体重指数、台阶实验、立定跳远、握力体重系数。
对于层次分析法,Saaty等人用实验的方法比较了在不同的标度下人们判断结果的准确性,实验结果也表明采用1-9标度最为合适[12]。为求出各项指标的权重分配,本文就根据Satty提出的属性间相对重要性等级表来构造比较判断矩阵,由经验确定同层各指标相对于上层总目标两两重要性的关系。设有m个目标方案或元素,根据重要性准则,将这m个目标两两进行比较,把第i个目标对第j个目标的相对重要性记为 aij(j=1,2,3,…,m).这样构造的 m 阶矩阵用于求解各个目标关于某准则的优先权重,成为权重解析判断矩阵,简称判断矩阵,记作 A=(aij)m×m.

为了确定判断矩阵的合理性,本文首先对所构造矩阵进行一致性检验,通过Matlab求解[6]所建立的判断矩阵A的最大特征值λmax=5.0264,经过计算发现所得的矩阵的的一致性指标CI=0.0066,一致性比率CR=0.0059<0.1.即认为所建立的判断矩阵可以接受。通过计算可以得到 μi=[0.1,0.1,0.175,0.45,0.175]T. 可得到五项指标的权重分别为:0.1,0.1,0.175,0.45,0.175.
2 灰色关联度综合评价模型
2.1 确定标准模式的指标集
针对于本文大学生体质健康的评价问题,首先寻找到一个各测试项目标准模式值,将各个学生的测试项目成绩与标准模式值进行灰色关联度分析,再通过加权得到综合关联度,通过比较关联度的大小,达到对大学生体质健康的科学评价。
根据现行《大学生体质健康标准》,本文用身体形态,身体机能,运动能力三个方面对大学生的体质健康进行评价,身体形态用克托莱指数[7](体重W/身高H×1000),克托莱指数是反映人身体形态发育水平和匀称程度的有效指标,为了建立一个简便、直观又能客观反应学生形态匀称度的指数标准,本文采用个体克托莱指数与同龄同性别的平均指数的比值作为新的指数,用这个新的指数来评价大学生的身体形态,所以标准模式指标数设为1,即个体W/H与平均W/H(19岁以上克托莱指数趋于稳定,其值为347)的比值越趋近于1表示此个体身体形态越匀称。身体机能用肺活量体重指数和台阶指数表示,这两个指标越趋近于极值表示身体机能越好,所以采用同龄同性别的测试极值作为其标准模式值。本文选择立定跳远和握力体重指数两个指标表示运动能力,这两个指标都是越趋于极值就越能体现其运动能力越强,他们的标准模式值也采用同龄同性别的测试极值表示。
本文随机抽取了2013年大学生五一数学建模竞赛试题中6名大学男生体质健康测试数据为例(见表1)。

表1 16名大学男生的各指标测试原始成绩
2.2 评价模型的建立与求解
2.2.1 对表3的数据进行规范化处理
为保证建立模型的质量和系统分析的正确性,对采集来的原始数据一般需进行预处理,使其消除量纲和具有可比性,即在关联度计算之前,对各要素的原始数据作初值变换或均值变换等,然后利用变换后所得数据作关联度计算,本文采用原始数据与标准数据之比来消除量纲;其标准模式为:
x0=(x0(1),x0(2),x0(3),x0(4),x0(5))=(1,105,100,2.9,100)
接下来对数据进行无量纲化处理:

其中 xi=(xi(1),xi(2),… xi(5)),i=0,1,2Λ 6,k=1,2,Λ,5.
2.2.2 计算各指标与标准模式指标的关联系数
x0受到多种因素 xi(i=1,2,…,6)的影响,一种利用因素 xi对因子x0的灰关联度来表示xi对x0影响大小的方法即称为灰关联分析。
系统行为因子x0的参考数列为:
x0={x0(k)|k=1,2,…,5}=(x0(1),x0(2),…,x0(5))
相关因素为 xi(i=1,2,…,10),即比较数列为:
xi={xi(k)|k=1,2,…,6}=(xi(1),xi(2),…,xi(5))
则参考数列对于各比较数列间的绝对差为:
△i(k)=|x0(k)-x0(k)| (k=1,2,…,5;1≤i≤6)
记△i=(△i(1),△i(2),…,△i(6)),称之为差数列。 于是定义比较数列xi对参考数列x0在第k点的灰关联系数为:

其中常数α∈[0,1],称为分辨率系数。显然,当α越大时,分辨率越大;当α越小时,分辨率越小,一般情况取α=0.5.对已规范化、量纲话后的体质项目测试数据与标准模式进行灰色关联计算得到如下表2。
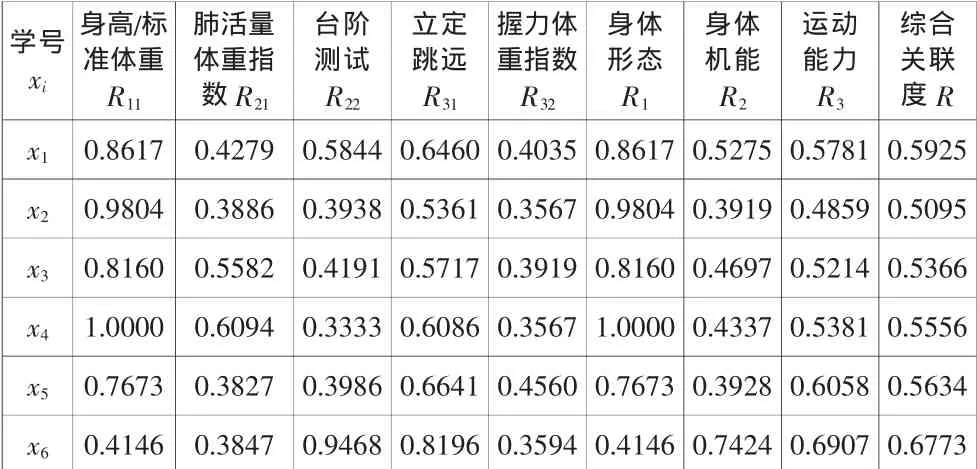
表2 各项目的关联系数
2.2.3 计算综合关联系数R
通过公式(1)计算“身体形态/身体机能/运动能力”各指标的关联Rl(l=1,2,3)系数及综合关联度 R。

按照综合关联度的大小得到6名学生的体质健康水平由优到劣的排名:x6,x1,x5,x4,x3,x2.
3 结束语
在大学生体质健康水平评价过程中存在着标准区分度不够,综合评价中原始测试数据信息丢失的问题,通过确定测试项目权重、建立灰色关联模式评价模型,计算学生各项目成绩与标准模式的关联系数和关联度,本文对学生的体质健康水平进行科学、准确的综合评价,客观的反映了个体学生的差异。亦可以通过模糊综合综合评判法确定学生各测试项目的动态加权函数,再通过综合指标函数对学生的体质健康进行评价。灰关联层次分析法也可以用于对水质、风险评估等评价类问题中。
该问题的解决有利于广大大学生以及家长客观、准确的了解学生的健康水平,督促学生积极参加体育锻炼,并为决策者提供更准确的学生的体质健康信息,具有重要的现实意义。
[1]杨进.武汉音乐学院大学生体质健康评价模型与干预对策研究[D].武汉体育学院,2009.
[2]武娇,顾兴全.灰关联模式评估模型在大学生体质健康水平综合评价中的应用[J].数学的实践与认识,2006,36(3):63-69.
[3]Hsu Liuhsiang,Ken Meilien, Lein.The evaluation of the supplier’s competencies for product innovation based on grey relational analysis a case for centrifugal pumps[J].Journal of Grey System,2008(3):55-5.
[4]Saaty T L,Ozdemir M.Negative priorities in the analytic hierarchy process[J].Mathematical and Computer Modelling,2003,37(9),1063-1076.
[5]王林,彭军武,陶武建.《学生体质健康标准(试行标准)》测试指标的可行性分析[J].北京体育大学学报,2006,29(2):256-258.
[6]丁毓峰.MATLAB从入门到精通[M].北京:化学工业出版社,2011.
[7]徐玉娥.大学生身高体重测评结果比较研究[J].陕西理工学院学报:自然科学版,2013,29(4):71-74.
