Numerical Solution for a Class of Linear System of Fractional Differential Equations by the Haar Wavelet Method and the Convergence Analysis

Yim ing Chen,Xiaoning Han and Lechun Liu

1 Introduction

In the past several decades,there has been a great deal of interest in fractional differential equations.Kai Diethelm has analyzed the fractional differential equations theoretically[Kai Diethelm(2004)]and mainly studied Volterra integral equations[Kai Diethelm and Neville,J.F(2012)];Mark M.Meerschaert has completed the stochastic models for fractional calculus[Mark M Meerschaert and A lla Sikorskii(2010)];Wen Chen has used fractional derivatives to study anomalous diffusion modeling[Chen,Sun,Zhang and Korosak(2010)];Changpin Li has done the asymptotical stability analysis of linear fractional differential systems[Li and Zhao(2009)]and studied the numerical algorithm for fractional calculus[Chen and Li(2012)]with An Chen.In recent years,the study of fractional calculus has turned to practical application from pure mathematical theory.Compare with integer order differential equation,fractional differential equation has the advantage that it can describe some natural physics processes and dynamic system processes much better[Chen,Sun,Zhang and Korosak(2010);Chen,Sun and Li(2010);Chen,Baleanu and Tenreiro Machado(2010)]Among all of them above,Haar method is the easier one to calculate.Because the range of Haar wavelet basis function only has three numbers:-1 0 and 1,Haar method can transform the fractional differential equations into a linear system of algebraic equations and there are many zero elements in the coefficient matrix In general,it is not simple to derive the analysis solutions to most of the fractional order differential equations Therefore,it is vital to develop some reliable and efficient techniques to solve the fractional differential equations.And the numerical solution of fractional differential equations has attached considerable attention from many researchers.During the past decades,an increasing number of numerical schemes are being developed.These methods include finite difference approximation method[Yuste(2006)],fractional linear multi-step method[Ford and Joseph Connolly(2009);Sweilam,Khader and Al-Bar(2007)],collocation method[Rawashdeh(2006);Li(2012)],the Adom ian decomposition method[Momani and Odibat(2007);Odibat and Momani(2008)]variational iteration method[Wu and Lee(2010);Odibat and Momani(2006)],and operational matrix method[Saharay(2012);Ü Lepik(2009);Li and Zhao(2010)]By now,most of the relevant literatures concern about the numerical solution of the fractional differential equations[Rawashdeh(2006);Li(2012);Wu and Lee(2010);Ü Lepik(2009);Li and Zhao(2010);Li and Fan(2012)],the existence and uniqueness of the solutions for system of fractional differential equations[Gao and Jiang(2013);Huang(2012);Duan(2009);Dai and Li(2012)],while the research about the numerical solution of the system of fractional differential equations is relatively fewer than others.

In the present paper,we intend to use the Haar wavelet method to solve a class of linear system of fractional differential equations as following:

whereanddare known constants,f1(t),f2(t),e1(t)ande2(t)are the functions in the Hilbert spaceWe adopt the Riemann-Liouville and Caputo fractional differential-integral definitions[Kilbas,Srivastava and Trujillo(2006)]as following:the relationship between Riemann-Liouville operator and Caputo operator is given by:

We expand the unknown functions as linear combination of wavelet basis functions with unknown coefficients,the method transforms the system of differential equations into a system of algebraic equations.

The paper is organized as follows.In section 2,the formulations of the Haar wavelet basis functions in the Hilbert spaceL2[0,T)are given,and then we get the operational matrix of Haar wavelet through the operational of Block Pulse Functions(BPF).In section 3,Haar wavelet method is used to approximate the system of fractional differential equations.As a result the system of fractional differential equations is converted into algebraic equations.In section 4,the convergence analysis of the Haar wavelet method is given.Numerical examples are given to demonstrate the validity of Haar wavelet method in solving fractional differential equation in Section 5.Section 6 comments on the result.

2 Haar wavelet and the related operational matrix

2.1 Haar function

The Haar wavelet is the function defined in the Hilbert spaceL2[0,T]

whereandJis a positive integer,so thati=1,2,3,···m−1m=2J+1.Each Haar wavelethihas the support interval

Any functionf(t)defined on the interval[0,T]can be expanded into Haar wavelet by

whereciare the Haar coefficients.So as to the following integral square errorεis minimized

we can get the explicit formulations ofci

Iff(t)is approximated as piece wise constant during each subinterval,(4)may be terminated after m terms,that is

whereCmandHm(t)are m-dimensional row vectors

Taking the collocation points as following

then we defined

Φm×mis a m-square Haar matrix.

2.2 Operational matrix

In this part,we’ll get the operational matrix of Haar wavelet through the operational of Block Pulse Functions(BPF).

The BPF defined as

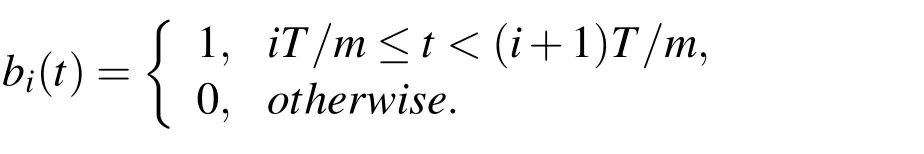
wherei=0,1,2,···,(m−1).Then we have

where

In Ref[Li and Sun(2011)],the Block Pulse operational matrix of the fractional order integrationFαhas given by

where

Let

the Haar wavelet operational matrix of the fractional order integrationis a m-square matrix.

Using Eqs.(7)(8)and(9),we have

namely

3 Application of Haar wavelet in system of fractional differential equations

The purpose of this paper is to present the numerical solution of the system of fractional differential equations as Eq.(1)

Let

by using Eqs(2)(9)and(10),we have similarly

substituting Eqs.(11)(13)for(1),we have

Thus Eq.(1)has been transformed into a system of algebraic equations.Discrete

Eq.(14)at the collocation points defined in Eq.(6),then we have

where

then Eq.(15)can be written as

The least squares solution of the above equationwhich calculated by MATLAB[Ge and Sha(2007);Zhang(2010)]programs can be regarded as the approximate solution.Substituting the values of the coefficientsandinto Eqs.(12)and(13),we get the output responseu(t)andv(t).

4 Convergence analysis of the Haar wavelet method

In this subsection,the convergence analysis of Haar wavelet method has been employed.In order to illustrate the convergence conveniently[Chen(2012)],let

so we have the orthogonal property of Haar wavelet

There are two error estimates has been defined:

(1)If the exact solution of the problem Eq.(1)is known asuex(t),uJ(t)is the numerical solution at the levelJthat calculated by Haar wavelet method.Let

where{tk}are the collocation points at the levelJ.Then we define the global error estimate as

Then we can have

whereandK>0

Proof.From the definition

Now,

applying mean value theorem:

whereandsubstituting Eq.(18)for Eq.(17),we have

(2)Mostly the exact solution is unknown,at the beginning,we solve the problem for the level ofJ,the result is denoted byuJ(t),then repeat these calculation forJ+1,getting in this way the functionuJ+1(t),next we define

the error estimate we shall define as

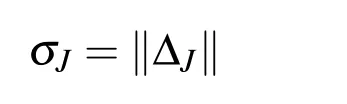
Theorem 4.2.Suppose thatuJ(t),uJ+1(t)is the approximate solutions,andσJis defined as above,then the error at Jth level satisfies the following inequality

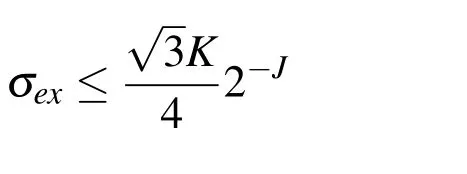
whereandK>0

Proof.From the properties of inequality

applying Lemma 6.1,we can see

From the Eqs.(19)and(20),it is obvious that the accuracy improves when we increase the level of resolutionJ

Because the value of the exact solution in boundary point has been given,so even if the derivative of exact solution in boundary point does not exist,nor can be an in finite value.So we can always find a suitable K to support the theorems 1,2.The derivatives of the selected points in the proof of theorems are the derivatives of interval internal points.So the above two theorems can also be applied to the situation that the derivative of exact solution in boundary point does not exist

5 Numerical exam ples

Example 1.Consider the following system of linear fractional differential equations

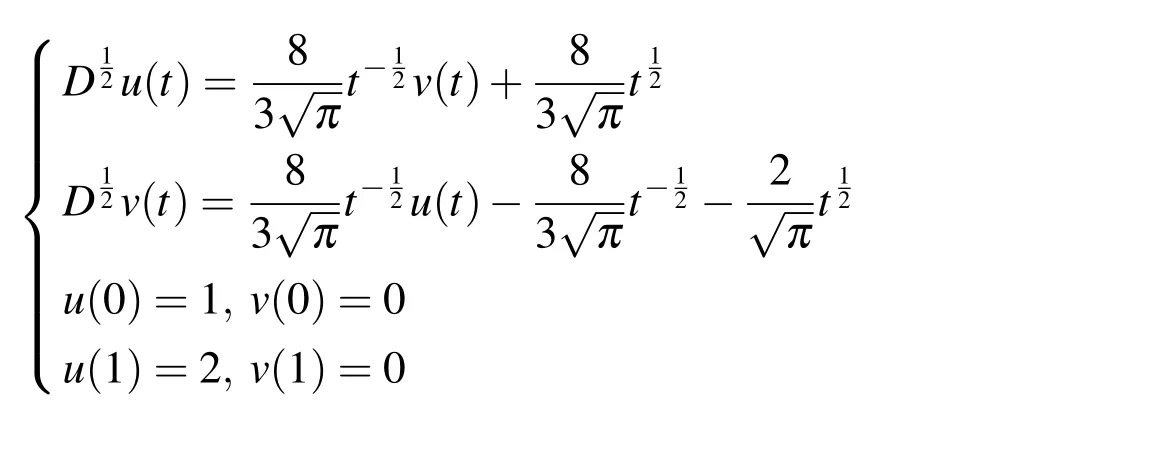
The exact solutions are given by.The comparison between approximate and exact solutions forj=5,T=1 is presented in Fig.1 and the errors ofu(t)v(t)for different values ofmare shown in Table 1 In the table we can see the accuracy improved when increasing the level of resolutionJ

Figure 1:The comparison between approximate and exact solutions of Example 1.

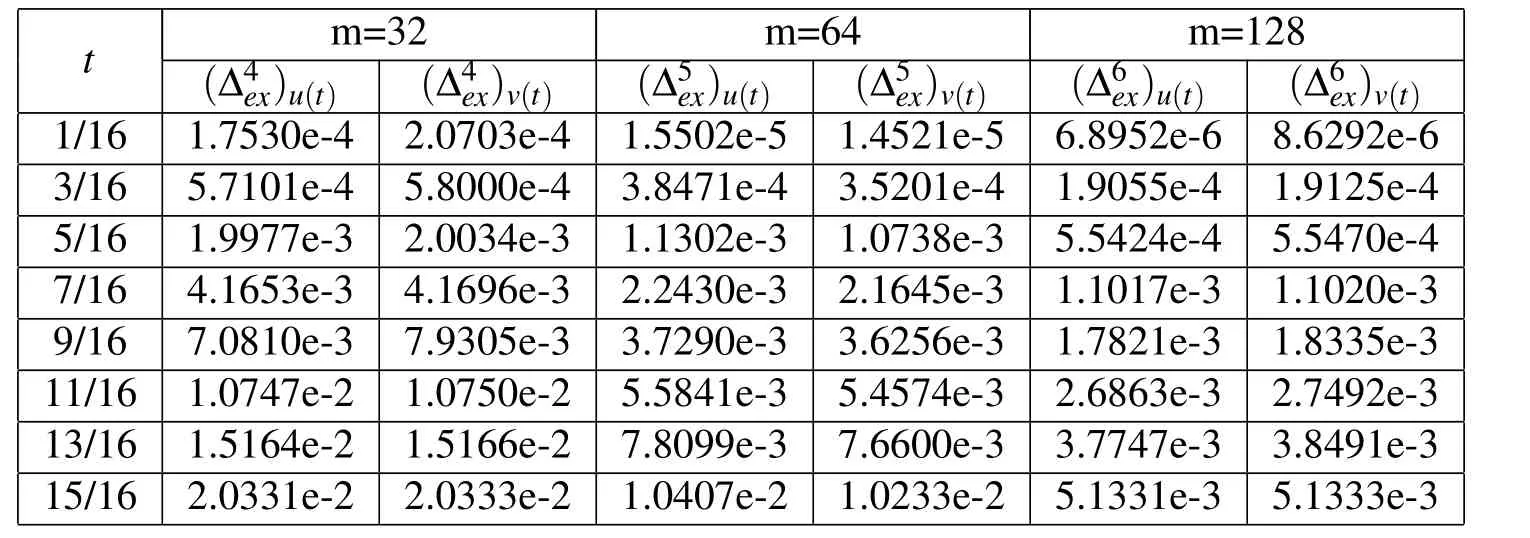
Table 1:Errors for different values of m.

Exam p le 2.Now,let us consider the following fractional equations:

The exact solutions of the system of equations areu(t)=t8−t7andv(t)=t6+2.The comparisons between approximate and exact solutions forj=5,T=1 are shown in Fig.2 which demonstrated the numerical solutions approximate the exact solutions in a good way.

Example 3.Consider the differential equations of fractional order

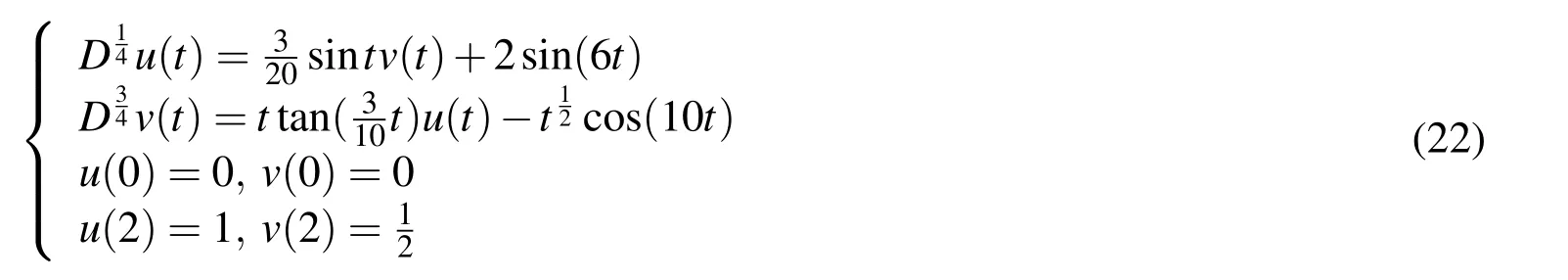
This system of fractional differential equations doesn’t have exact solutions,and the approximate solutions forJ=4,T=2andJ=5,T=2are shown inFig.3.FromTable 2we can see the errors for different values ofJ

6 Conclusions

Figure 2:The comparison between approximate and exact solutions of Example 2.

Figure 3:The approximate solutions of Example 3 for m=32 and m=64.

Table 2:Errors for different values of m.

This article adopts Haar wavelet method to solve a class of linear system of fractional differential equations by combining wavelet function with operational matrix of fractional integration.In order to reduce the computation,we transform the initial equations into a linear system of algebraic equations.In fortunately,there are many zero elements in the coefficient matrix.efficiency of this method is demonstrated by the convergence analysis and three numerical examples It is obvious that the accuracy improves when we increase the level of resolutionJUsually,it can reach the higher precision,even thoughJis small

Acknowledgement:This work is supported by the Natural Foundation of Hebei Province(A2012203407).This work is supported by Qinhuangdao research and development program of science and technology,Adaptive Boundary Element Method of precision rolling process simulation(201201B019).This work is supported by Qinhuangdao Technology Bureau 2013 research and development projects of science and technology(201302A023).

Chen,A.;Li,C.P.(2012):Numerical Algorithm for Fractional Calculus Based on Chebyshev Polynomial Approximation.Journal of Shanghai University(Natural Science Edition)vol.18,pp.47-53.

Chen,W;Sun,H.G.;Li,X.S.(2010):The fractional order derivative modeling of mechanics and engineering.Science Press.

Chen,W.;Baleanu,D.;Tenreiro M achado J.A.(2010):Special issue of computers and mathematics with applications on fractional differentiation and its applications Preface.Computers and Mathematics with Applications,vol.59,pp.1585.

Chen,W.;Sun,H.G.;Zhang,X.D.;Korosak D.(2010):Anomalous diffusion modeling by fractal and fractional derivatives.Computers&Mathematics with Applications,vol.59,pp.1754-1758.

Chen,Y.(2012):Error analysis for numerical solution of fractional differential equation by Haar wavelets method.Comput.Sci,vol.5,pp.367-373.

Dai,Q.;Li,H.L.(2012):Blowing-up solutions of a type of fractional differential equations.Journal of Jilin University,vol.50,pp.1-5.

Diethelm,K.(2004):The Analysis of Fractional Differential Equations.Spriger.

Diethelm,K.;Neville,J.F.(2012):Volterra integral equations and fractional calculus:Do neighboring solutions intersect?J.Integral Equations Applications,vol.24,pp.2537.

Duan,J.S.(2009):Solution for system of linear fractional differential equations with constant coefficients.J.of Math,vol.29,pp.599-603.

Ford,N.J.;Connolly,J.A.(2009):Systems-based decomposition schemes for the approximate solution of multi-term fractional differential equations.Comput Appl Mathvol.229,pp.382-391.

Gao,F.;Jiang,W.H.(2013):Existence of solutions for boundary value problem of fractional differential equation system.Mathematics in Practice and Theory,vol.43,pp.254-260.

Ge,Z.X.;Sha,W.(2007):Wavelet Analysis Theorem and MATLAB Application.Electronic Industrial Publication.Beijing.

Huang,Y.H.(2012):Positive solutions to Dirichlet-type boundary value problems of singular coupled systems of fractional differential equations.Mathematics in Practice and Theory,vol.42,pp.228-234.

Kilbas,A.A.;Srivastava,H.H.;Trujillo,J.J.(2006):Theory and applications of fractional differential equations.Amsterdam Elsevier Science B.V.

Lepik,Ü.(2009):Solving fractional integral equations by the Haar wavelet method.Applied Mathematics and Computation,vol.214,pp.468-478.

Li,C.P.;Zhao,Z.G.(2009):Asymptotical stability analysis of linear fractional differential systems.Journal of Shanghai University(English Edition)vol.13,pp.197206.

Li,Y.L.;Sun,N.(2011):Numerical solution of fractional differential equations using the generalized block pulse operational matrix.Computers and Mathematics with Applications,vol.62,pp.1046-1054.

Li,X.X.(2012):Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method.Commun Nonlinear Sci Numer Simulat,vol.17,pp.3934-3946.

Li,Y.L.;Zhao,W.W.(2010):Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations.Applied Mathematics and Computation,vol.216,pp.2276-2285.

Li,Z.;Fan,Q.B.(2012):Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet.Commun Nonlinear Sci Numer Simulat,vol.(17),pp.2333-2341.

Meerschaert,M.M.;Sikorskii,A.(2010):Stochastic Models for Fractional Calculus.Mathematics Subject Classification.

M omani,S.;Odibat,Z.(2007):Numerical approach to differential equations of fractional order.Comput Appl Math,vol.1,pp.96-110.

Odibat,Z.;M omani,S.(2008):Numerical methods for nonlinear partial differential equations of fractional order.Appl Math Model,vol.32,pp.28-39.

Odibat,Z.;M omani,S.(2006):Applivation of variational iteration method to equations of fractional order.Int J Nonlinear Sci Numer Simul,vol.7,pp.271-279.

Rawashdeh,E.A.(2006):Numerical solution of fractional integro-differential equations by collocation method.Appl Math Comput,vol.176,pp.1-6.

Saha Ray,S.(2012):On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley Torvik equation.Applied Mathematics and Computation,vol.218,pp.5239-5248.

Sweilam,N.H.;Khader,M.M.;Al-Bar,R.F.(2007):Numerical studies for a multi-order fractional differential equation.Phys Lett A,vol.371,pp.26-33

Wu,G.;Lee,E.W.M.(2010):Fractional variational iteration method and its application.Phys Lett A,vol.374,pp.2506-2509.

Yuste,S.B.(2006):Weighted average finite difference methods for fractional diffusion equations.Comput Phys,vol.216,pp.264-274.

Zhang,D.F.(2010):Matlab Numerical Calculation Method.China Machine Press.