第八届国际天文与天体物理奥林匹克竞赛理论试题（上）

□ 供稿 / IOAA组委会 翻译 / 戴岩

第八届国际天文与天体物理奥林匹克竞赛理论试题（上）

□ 供稿 / IOAA组委会 翻译 / 戴岩

短问题

1.拉格朗日点

小物体在只受引力作用下绕两个大质量物体作圆周运动的过程中，轨道系统中会包含五个拉格朗日点。例如人造卫星相对地球和月亮运动，或者卫星相对地球和太阳运动。图1中给出了日地系统中拉格朗日点L的两个可能的位置L133和 L32，一个在地球围绕太阳运动的轨道以内，一个在地球围绕太阳运动的轨道以外。

请找出L31和 L32中哪个才是真正的拉格朗日点L3，证明你的结论，并求出太阳到拉格朗日点L3的距离和日地距离相比的差。

已知日地距离为dES=14.96.107km，地球和太阳的质量满足ME/MS=1/332946。

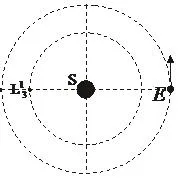
图1A

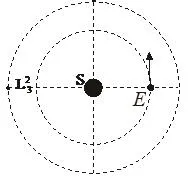
图1B

2. 太阳的引力灾变

一次引力灾变使太阳瞬间损失了一半的质量。如果假定地球的轨道是椭圆的，轨道周期是T0=1年，地球轨道的椭率是e0=0.0167。

分别计算在以下时间发生引力灾变后地球轨道的运动周期：

（1）7月3日（远日点）；（2）1月3日。

3.宇宙辐射

在研究宇宙辐射时，认证了一种中性不稳定的粒子——π0介子。π0的静止质量比电子的静止质量大得多。研究发现，它在飞行过程中分解成了两个光子。在一种特定情况下，一个产生的光子具有最大的能量Emax，此时另一个产生的光子则具有最小的能量Emin。

请以Emax和Emin为已知量，推导π0介子分解前初速度的表达式。

已知c表示光速，且相对论粒子的能量和动量满足E2=p2c2+m02c4。

4. 桑德拉·布鲁克和乔治·布鲁尼

一个质量为M=100kg的宇航员出舱执行修理卫星的任务。卫星相对太空船静止，间距为d=90m。维修任务结束后，宇航员发现返航系统出现故障。他身上带的空气给养只能再支持3分钟。他的手套上结实地绑有一个密封了m=200g冰的圆柱形罐头（横截面积为S=30cm2）。罐子里的冰并不是满满一罐。

如果宇航员沿着正确的方向打开罐头，请确定他能否在空气给养耗尽前平安返回太空船，并通过计算说明。宇航员不能丢下任何装备或者通过触碰卫星借力。

已知如下数据：罐头中冰的温度T=272K，在T=272K时所对应的水的饱和蒸汽压为Ps=550Pa，宇宙气体常数R=8300J/（kmol.K），水的摩尔质量μ=10kg/kmol。

5. 一颗主序星的寿命

图5给出了根据观测大量恒星得到的质光函数log（L/ Ls）=f（log（M/Ms））关系图。L和M代表一颗恒星的光度和质量，Ls和Ms代表太阳的光度和质量。

已知太阳在主序阶段的寿命是τs，一颗恒星的质量转化成能量的百分率是η，太阳的质量转化成能量的百分率是ηs，恒星的质量是太阳质量的n倍，即n=M/Ms，并假设恒星在主序阶段的光度是保持不变的。请推导这颗恒星在主序阶段的寿命的表达式。

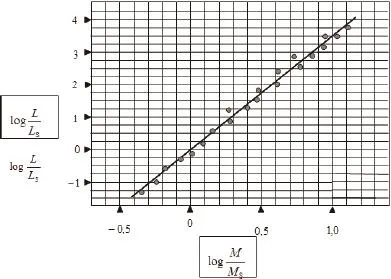
图5

6.恒星表面的有效温度

研究一颗恒星的两种辐射，它们的波长都在一个窄小的波段内（△λ〈〈λ），即在λ到λ+△λ之间。根据普朗克定律（对于绝对黑体），已知如下关系：r=2πhc2/λ5（ehc/kλT-1）。该式表示了，单位时间、恒星表面单位面积、单位波长间隔内，恒星所释放的能量。在地球上测得，变化范围均在△λ内的两种辐射（波长分别为λ1和λ2）的光谱辐射强度分别是I1（λ1）和I2（λ2）（不需考虑大气影响）。

如果光谱辐射强度满足I1（λ1）=2I2（λ2），且hc〈〈λkT，请推导两种辐射的波长λ1和λ2之间的关系。

已知：h代表普朗克常数，k代表玻尔兹曼常数，c代表真空中的光速，当x〈〈1时ex≈1+x。

7.光压

对于地球上的观测者，接收到的来自太阳的压力为prad,s，接收到的来自某一颗恒星∑的压力是prad,∑。如果太阳的视星等是ms，请推导恒星∑的视星等。

以下提示可能有助于你解题：通常，电磁辐射的压力等于电磁辐射的能量密度（prad=△E/△V）。

已知太阳的质量为Ms，太阳的半径为Rs，宇宙引力常数为G，斯蒂芬-玻尔兹曼常数为σ，真空中的光速为c。

8.绕日运动的太空船

一艘球形太空船在以圆轨道绕太阳运动，并绕垂直轨道面的轴自转。飞船外表面的温度是TN。假定太空船是理想黑体，且飞船内部没有活动。

计算太空船中的宇航员看到的太阳的视星等和角直径。已知TS代表太阳的有效温度，RS代表太阳半径，d0代表日地距离，m0代表太阳在地球表面的视星等，RN代表太空船的半径。

9.镜中织女

如图所示，在相机物镜的光轴上有一个平面镜。镜子的长度等于物镜焦距的一半。相机的焦面上放置了一张照相底片。底片上捕获了两个亮度不同的图像。织女星不在透镜的光轴上。图像∑1到光轴的距离是r/2。

试求底片上的两个织女星图像的星等差。

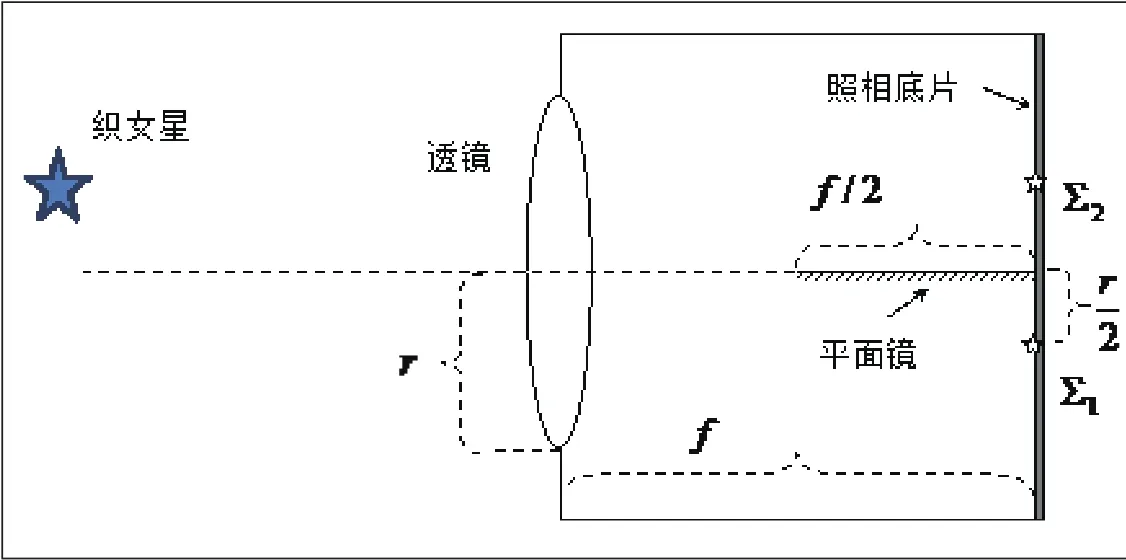
图9

10.以罗马尼亚语命名的星星

两个罗马尼亚天文学家最近发现了两颗变星。两颗恒星的银经和银纬分别是：Galati V1（l1=144.371°，b1=-11.35°）和Galati V2（l2=113.266°，b2=-16.177°）。

请计算Galati V1 和 Galati V2之间的角距离。

11.举头望月识星等

已知从太阳上看月球的视星等是MM=0.25m。

请分别计算满月和上弦月月相时从地球上看到的月球的视星等。

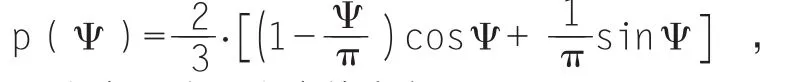
12. 造父变星的绝对星等

造父变星是变星的一类，它们光度的变化取决于星体的脉动。已知一颗造父变星的脉动周期满足：P=2πR R/GM，其中R代表造父变星的平均半径，M代表造父变星的质量（脉动期间为常量）。假定脉动期间恒星的温度为常数。

证明造父变星的绝对星等Mcep可以表示为如下函数形式：Mcep=-2.5m.logk-（10/3）m.logP，其中P为造父变星的脉动周期。（未完待续）