问题驱动式教学法在数值分析中的应用与研究——以插值法为例

梅 芳 王巧玲 曾春华

（江西农业大学 理学院，江西 南昌 330045）

问题驱动式教学法是基于问题的教学方法，一种建立在构建主义教学理论基础上的教学法，它要求“问题”的目标性和教学情景的创建，学生在老师的帮助下，紧紧围绕共同的任务，在强烈的真实问题动机的驱动下，通过对资源的积极主动应用，进行自主探索和互动协作的学习。

目前国内大学《数值分析》课程的教学改革起步晚，注重纯理论教学。教学过程中存在的不足：数学理论推导严密但是教学枯燥，学生学习缺乏兴趣。国外《数值分析》课程的改革走在前沿，美国工程院院士Cleve Moler在20世纪70年代提出在学习方式上,将教师引导与学生自主探究、合作交流有机结合起来。注意吸收计算数学中算法研究的最新理论研究成果，让学生在真实的问题驱动下，带着问题去学习领会蕴含其中的算法原理,并能运用所学理论分析利用数学软件解决现实生活中的科学问题。但对驱动问题的解决措施的探讨深入不够。

本文以数值分析课程的插值法为例，介绍问题驱动式教学法在整个章节课堂教学中的研究与应用。

1 创设问题情境，提出问题

函数是描述自然界客观规律的重要工具，实际应用中许多函数是通过实验或者观测得到的，其形式是一张函数表，作一条曲线，其类型（代数多项式函数，三角函数，指数函数……）是事先人为给定的，该曲线经过所有点(xi,yi),i=0,1,2,…,n，这就是所谓的插值问题。

据资料记载，某地某年间隔30天的日落时间如下：

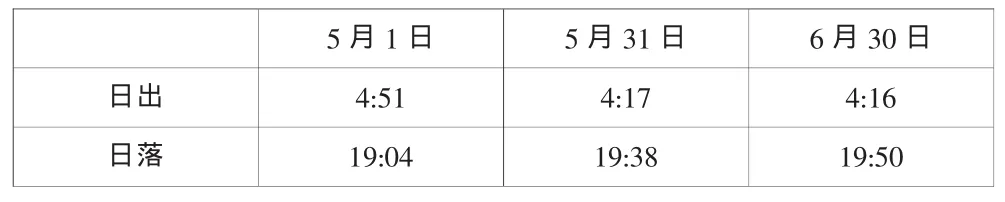
5月1日 5月31日 6月30日日出 4:51 4:17 4:16日落 19:04 19:38 19:50

根据上述资料，计算这一年中哪一天白天“最长”。

2 引导学生讨论交流，解决问题

让学生查找资料，分组讨论，了解插值法的产生背景，中外数学家在此问题上研究的进程，这种古老的分析问题数学方法应用在那些课题中？分析关于多项式插值的理论依据是什么？提出问题对于函数y=f(x)是否存在这样的多项式函数P(x)能精确的逼近它呢？经过数学的推导得到结论：满足给定区间[a,b]上 n+1 个点 a≤x0＜x1＜…＜xn≤b 上的函数值为y=f(xi)(i=0,1,…,n)的插值多项式P(x)存在且唯一。

然后得到Lagrange插值法的计算公式：

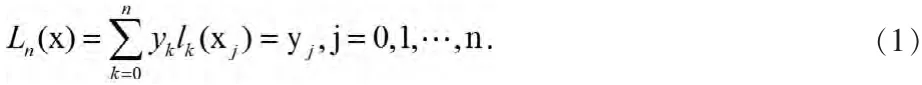
其中

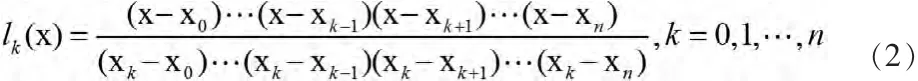
插值余项与误差估计：

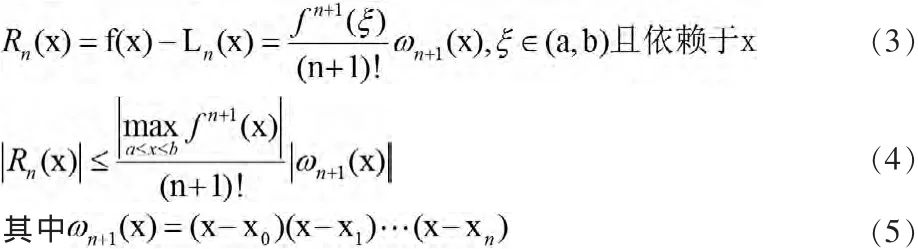
接下来，按上面的理论知识，求解提出的问题，建立一个简单的数学模型，用二次等距离插值法计算求解：

5月1日设为第0天，则x=0

再设每一天白天的长度（日出与日落的时数）为14小时13分+T分

故天数和它的长度可用(x,T)表示。有记载的三天数据对应于(0,0),(30,68),(60,81)

由微积分中的最值原理T'(x)=0,得到x≈52.09，也就是最长的一天为5月1日以后的第52天，即6月22日，T=83分，这一天日出与日落之间的时数为14小时13分+83分=15小时36分。与每年的夏至节气日期相吻合。

然后拓展数值分析插值法数学实验，计算一年中的24节气所在的具体日期。

3 解决问题的基础上，进一步了解插值法在理论和实践上发展，应用的广泛性，提出新问题和知识延拓

Lagrange插值公式结构紧凑，思路清晰，程序编制容易，但是增减节点时，计算要全部重新计算，很不方便，增加计算量，我们希望在增加新的节点时，原先计算的结果对后来的计算过程仍然有用，那如何改进？于是我们得到Newton插值多项式

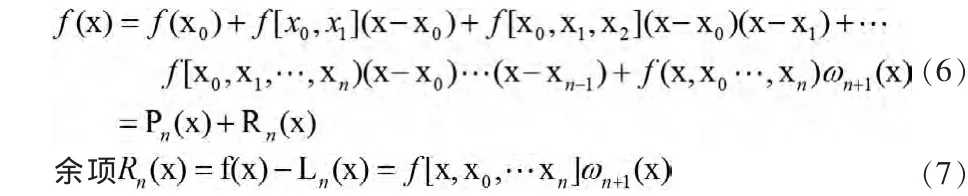
其中 ωn+1(x)由（5）式定义。

插值多项式要求插值节点相等，而实际问题中还经常要求节点上的导数值相等，甚至高阶导数值也相等，于是课题条件改变了，我们讨论新的解决问题的方法Hermite插值法。这类型的一般问题显然会具有些令人感兴趣的困难，在称为伯格霍夫插值的专题中奉献了大量的近期研究文献，学生可以查阅。

其它的插值法，早期的板材曲线切割时，常常把富有弹性的细长木条（样条）固定在样点上，比方说航空造船等工程设计的需要，要求样条曲线二阶导数连续，三次样条函数插值是被认为一种有效的数学工具，并且学生将看到，插值法的算法有很多种，针对问题选择方法十分关键，正确选择算法的前提是对方法的理解、分析、评价和鉴赏。

4 归纳解决问题中的知识点，强化系统认知能力，完善问题的结论，总结规律，提出更深一步的问题

插值法是一个古老而实用的方法，作为逼近函数的构造方法，是数值微积分，函数逼近，微分方程数值解的基础。因为高次插值的Runge现象，随着信息量的增加，实验的结果与直观的想象不吻合，它也是数值计算研究中值得高度重视的一类现象，也就是说Lagrange插值多项式的次数不可能无限制的增大，所以它没有实用性，采用分段低次插值，特别是三次样条插值，具有良好的收敛性与稳定性，理论上和应用上意义重要，在计算机图形学中有重要应用。

数值分析是研究用数学方法处理信息的学科，仅仅是实用信息量大，如果使用方法不当，也不能保证所得结果的正确性，在教学过程中提出一种知识建模化的问题驱动式教学方法，把学生在现实生活中感兴趣的相关问题，引入数值分析算法的教学之中，将问题驱动与数值分析的各种算法技术相结合，加深对《数值分析》这门课程的有关算法和结论的理解，激发学生积极思考和避免一些常犯易犯的错误，提出一种实用有效的问题驱动的教学内容结构设计，打破传统的教学模式，让数值分析的学习更高效。

［1］李庆扬,王超能,易大义.数值分析[M].5版.北京:清华大学出版社,2008：22-46.

［2］林成森.数值分析[M].2版.北京:科学出版社,2005:114-190.

［3］白峰杉.数值分析引论[M].2版.北京：高等教育出版社,2010:92-104.

［4］任玉杰.数值分析及其MATLAB实现[M].北京：高等教育出版社,2008:354-480.

［5］王国荣,俞耀明,徐兆亮.数值分析（原书第3版）[M].北京：机械工业出版社,2005:245-306.

［6］王超能.数值分析简明教程[M].北京：高等教育出版社,2003:13-53.