力限振动试验技术应用与研究

游亚飞，高宝玉，李光远，于学武

（中国航空综合技术研究所，北京 100028）

力限振动试验技术应用与研究

游亚飞，高宝玉，李光远，于学武

（中国航空综合技术研究所，北京 100028）

首先介绍传统加速度振动试验产生过试验的主要原因；接着介绍机械阻抗特性，给出视在质量、有效质量及剩余质量的定义；然后通过对复杂二自由度方法进行理论推导，给出力限试验条件的制定方法；最后以铝板为例，建立典型力限控制试验方案，提出力限试验方法及试验步骤。从试验结果看，力限控制试验方法是缓解试件过试验的一种有效方法。

力限；振动；复杂二自由度方法

前言

传统的振动试验一般采用加速度输入控制的试验方法，即控制试件与振动台或夹具界面处的加速度来模拟试件实际经受的力学环境。理论上，如果边界条件与实际使用环境一致时，试验条件（加速度控制曲线）应与实际使用时界面处的加速度响应谱一致，但实际情况并非如此，这主要是由于包络法制定加速度试验条件、机械阻抗不匹配和吸振现象三个方面原因造成的。

力限控制试验方法在GJB 150.16A《军用装备实验室环境试验方法》中明确提出，其基本原理是直接对支撑系统和试件之间的输入力进行控制，回避机械阻抗不匹配的问题。力限谱可根据加速度输入谱计算得到，该方法和加速度限控制方法一样，一般需要和振动加速度输入控制方法一起进行联合控制，力谱的频带通常限制在产品前几阶模态范围内，用于控制产品前几阶模态处的响应，加速度谱用于控制其它频带，最终控制的结果是在产品前几阶共振频率处，振动加速度功率谱密度响应特性曲线出现“凹谷”效应，有效防止了过试验的产生。

1 结构机械阻抗特性

1.1 视在质量

结构的视在质量是指界面力与界面加速度的比值，即界面力与加速度的传递函数，也被称为动力学质量。它是复数形式的，含有幅值和相位的信息。反映了结构的质量、刚度、阻尼特性。视在质量是随着频率变化的，在结构的固有频率处产生峰值，它可以描述连接界面处的动力学传递特性。结构视在质量公式见公式（1）。

其中：

ω为频率；M为视在质量；F为界面力；A为界面加速度。

1.2 有效质量

有效质量又称有效模态质量，通常可用有限元软件NASTRAN/PATRAN计算得出。结构的每阶模态可表示成一个单自由度弹簧质量系统。这些单自由度弹簧质量系统的质量就是有效质量。每阶模态的有效质量大小表征了该模态对单自由度弹簧质量系统视在质量的贡献。对于一个激励轴向，所有模态有效质量的和等于结构的总质量。有效质量的概念非常重要，它量化了结构质量与频率的关系，有助于对结构动态特性的理解和力限试验条件的制定。

1.3 剩余质量

激励频率以上结构固有频率所对应的有效质量之和称为剩余质量。系统第K阶模态的剩余质量见公式（2）：

n为结构内部自由度数。

2 力限条件的确定方法

2.1 引言

力限条件的确定是实现力限控制试验的前提。目前主要有三种方法计算力限试验条件：简单二自由度方法、复杂二自由度方法和半经验方法。本文主要根据NASA文献《Force Limited Vibration Testing Monngraph》中相关内容对力限试验方法进行研究，对复杂二自由度方法进行详细推导，为力限控制试验的应用提供输入。

2.2 复杂二自由度方法原理

支撑系统和试件各用了两个质量单元来表示系统的有效质量和剩余质量，如图1所示。其中，m1和m2分别为支撑系统和试件的有效质量，M1和M2分别为支撑系统和试件的剩余质量，c1和c2分别为支撑系统和试件的模态阻尼，k1和k2分别为支撑系统和试件的模态刚度，Fe为所受外力。

视在质量为

由于复杂二自由度系统处零频外，还有两个固有频率，系统的加速度响应在这两个固有频率点达到最大值，为计算该系统得到的最大界面力，首先需要求得该系统的两个固有频率。该系统无阻尼弹性共振频率的特征方程见公式（5）：

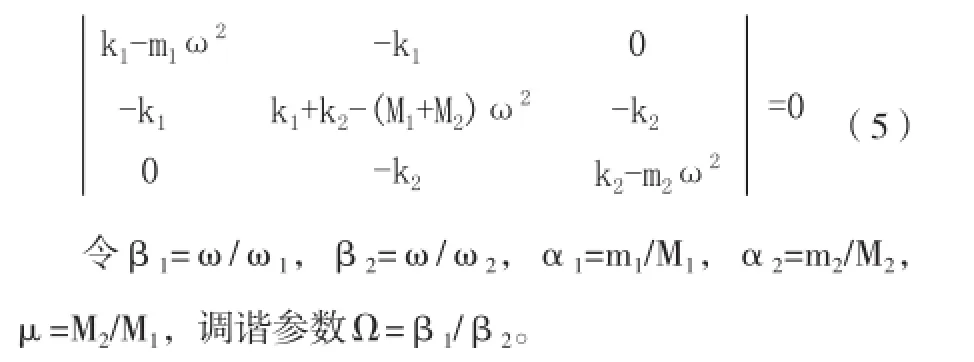
除去方程的两个零根后，可求得公式（10）的解为：

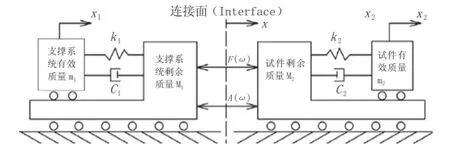
图1 复杂二自由度系统模型

假设复杂二自由度系统的激励Fe为一定值。对应两个固有频率点的W+interf和W-interf幅值的比值见公式（7）：

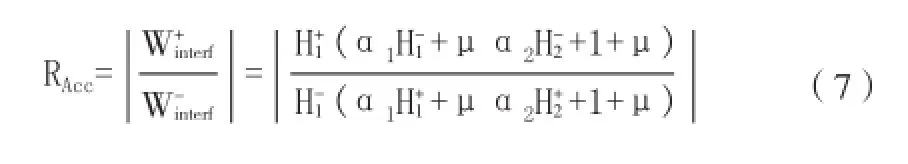
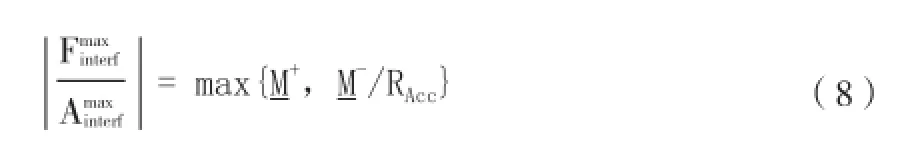
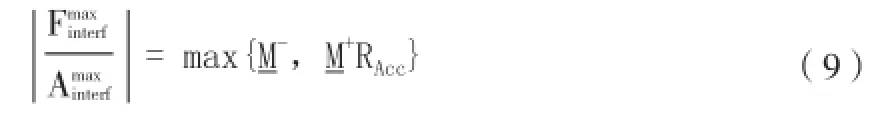
力限条件正则化系数γ为：

改变调谐参数Ω的值以确保对复杂二自由度所有的质量、刚度和阻尼组合都能找到界面力的最大值。根据《Force Limited Vibration Testing Monograph》中建议Ω∈[1/2，2] ，步长为1/16。力限条件如公式（11）所示：

2.3 复杂二自由度方法计算步骤

复杂二自由度方法计算力限试验条件实施过程如图2。

3 力限控制试验方法验证

3.1 力限试验控制原理

《Force Limited Vibration Testing Monngraph》中提出力限控制试验的双控方理论。图3为力限控制试验控制原理图。由图3可以看出，进行试验时，控制系统按照普通加速度试验条件控制，对安装在试件和支撑系统之间的力信号进行监测，当力响应信号过大，超过力试验条件时，实时调节振动台对试件的加速度输入，将界面力响应限制在力试验条件范围内，从而减轻试件的过试验。工程实际中力限通常只在试件共振频率处起作用[2]。

3.2 力限试验应用

3.2.1 试件与支撑系统

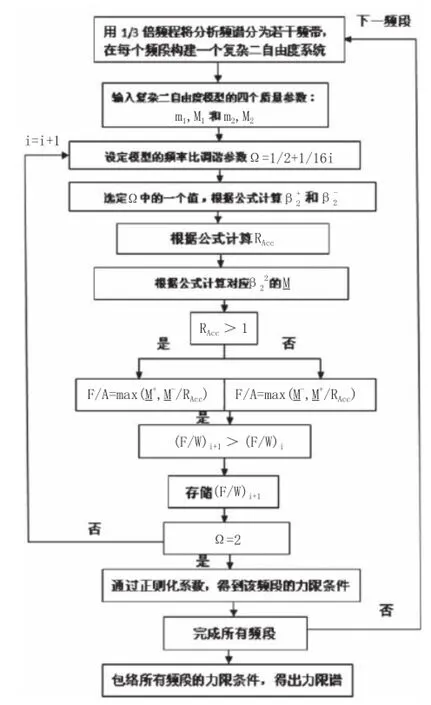
图2 复杂二自由度方法计算力限试验条件实施程序

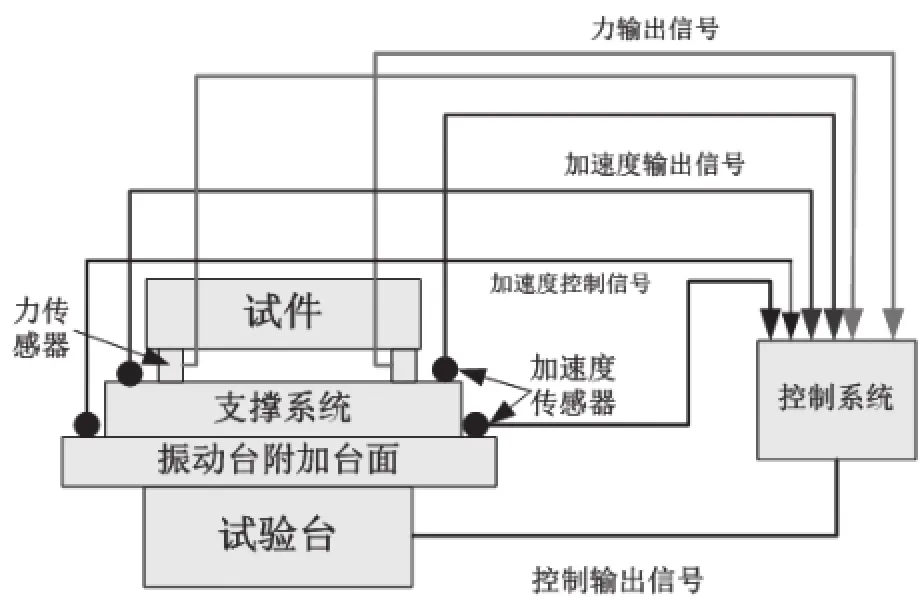
图3 力限控制试验原理图

试件为450mm×450mm×10mm (长×宽×高)方形薄板，支撑系统为600mm×600mm×10mm (长×宽×高)方形薄板，两者材料均为铝合金，牌号为6061，泊松比为0.33NA，质量密度为2700kg/m3。试件上有4个M10的穿孔，用于连接力传感器和支撑系统；支撑系统上除了安装试件的4个M10穿孔外，还有4个M12的穿孔用于连接振动台附加台面。

3.2.2 试验设备

本方案选择的力传感器为某公司生产的YDL-2H压电力传感器，其测量范围为50KN。为了控制和测量加速度值，还需使用加速度传感器。本方案选取的加速度传感器为BK4371V压电式加速度传感器。除了力测量设备外，还需能够测量力信号并进行适时控制的闭环回路的控制系统。本方案使用的控制系统为某公司生产的SUPER VT-9008数字式振动控制仪，该控制仪具备8个输入通道和2个输出通道。

3.3 试验实施方案

力限控制试验实施方案一般分为以下步骤：

步骤1：有限元模型的确定。首先用锤击法得出相关的模态参数（也可用正弦扫频得出），然后用有限元软件计算相关模态参数，修正有限元模型；

步骤2：对试件和支撑系统耦合所得系统（以下简称耦合系统）进行小量级的振动试验；

步骤3：获取界面处加速度试验条件。测量耦合系统界面处加速度响应量值，并进行最大值包络，作为试件单独振动的试验条件；

步骤4：获取界面处力试验条件。用图3中介绍的复杂二自由度耦合分析方法计算力试验条件（其中界面处加速度谱为步骤3中得到的加速度最大值包络）；

步骤5：验证力限试验的优势和有效性。首先对试件进行加速度控制试验，然后对试件进行力限控制试验，对比分析两种试验结果，验证力限控制的优势和有效性。

下面将逐一分析各步骤的实施过程。

3.3.1 步骤1：有限元模型的确定

首先使用LMS Test.lab软件对试件和支撑系统进行模态测试，得到固有频率，然后使用有限元分析软件对试件及支撑系统进行有限元模态分析，得到试件、支撑系统和耦合系统的有效质量、固有频率等参数，利用模态参数对有限元模型进行必要修正，从而得到比较精确的有限元模型。

1）锤击法确定模态参数

为得到试件和支撑系统约束模态参数，首先将试件和支撑系统按照实际状态安装，在试件上进行网格划分，对其进行模态试验；然后挪去试件，在支撑系统上进行网格划分，对其进行模态试验。试验时，使用LMS Test.lab软件对试验件进行模态测试，测试时使用的传感器为某公司4508型ICP传感器。按照顺序依次敲击试件和支撑系统的16个点，每个点重复敲击4次，对4个信号取平均，消除干扰信号，提高信噪比。在动态信号分析中对力信号和响应信号分别加力窗和指数窗来提高提取信号的质量，信号采用频率设为4096Hz。

2）有限元分析法确定模态参数

使用有限元计算软件计算得到试件、支撑系统及试件和耦合系统的固有频率和有效质量。有限元模型采用四面体网格划分，约束方式为四点固支。试件有限元模型共277个有限单元，2175个节点；支撑系统有限元模型共有469个单元，3682个节点；耦合系统有限元模型有746个单元，5857个节点。

3）两种方法获得参数对比

对比模态试验数据和仿真计算数据可以发现，通过仿真计算得到的模态质量贡献度较小的模态可能在试验中无法识别，所以仅选取仿真计算中模态质量贡献度较大的模态和模态试验识别到的模态进行对比，各模态对应的模态频率详见表1。由表1可以看出，有限元模型较为准确，其参数误差均不超过5%，因此无须对该模型进行修正。

3.3.2 步骤2：对耦合系统进行小量级的振动试验

在支撑系统和振动台附加台面之间4个连接点各垫装1个螺母，采用4点固支方式；在支撑系统和试件之间安装4个力传感器，用于测量两者之间的界面力。在振动台附加台面对角位置处各安装一个加速度传感器作为加速度控制传感器；在支撑系统另一对对角位置处各安装一个加速度传感器，用以测量安装界面的加速度响应。传感器的安装图如图4所示。

耦合系统随机振动试验的试验量级确定为2.7g，加速度试验条件如表2所示。

图5为加速度功率谱密度控制和界面加速度响应曲线，图6界面力功率谱密度响应曲线。

3.4.3 步骤3：获取界面处加速度试验条件

对界面处的加速度功率谱做包络，得到的加速度试验条件如图7所示。由图可以看出，绿色曲线是实测响应谱，红色曲线是对实测响应谱进行包络得到的实测上限谱。黑色曲线是根据NASA-HDBK-7005《Dynamic environmental criteria》，从实测上限谱中选取一定数量的频点，并对个别谱峰进行工程化削峰处理，最后进行平滑连接确定得到的试验规范谱。试验量级为8.59g。

3.4.4 步骤4：获取界面处力试验条件

试验采用的力限控制试验方案是对每个力传感器侧得到的力均进行限制，认为每个力传感器测到的力相等，均等于界面合力的1/4，对四个力传感器制定统一的试验条件。

表1 模态频率对比结果

图4 传感器的安装图

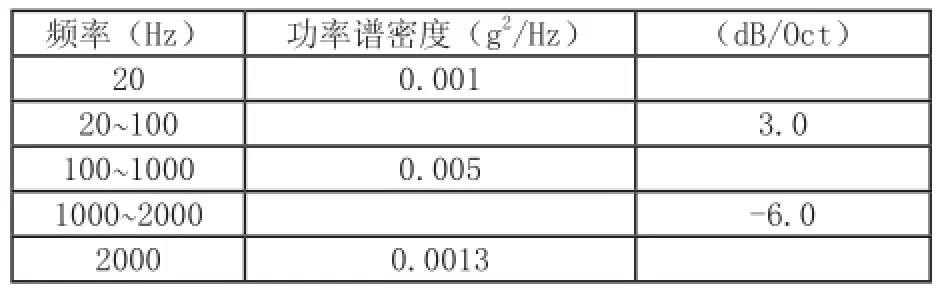
表2 随机加速度试验条件

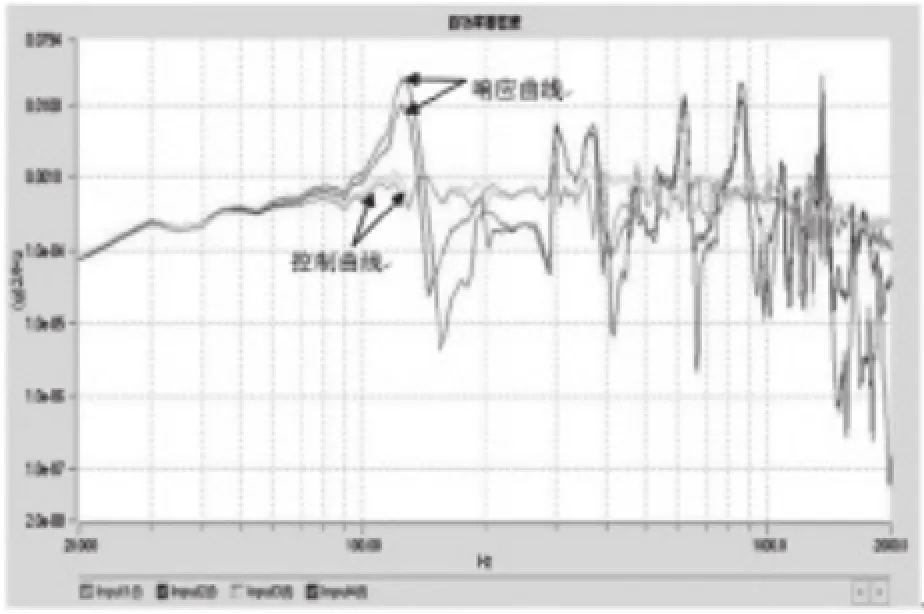
图5 加速度功率谱密度控制和响应曲线

图6 力功率谱密度响应曲线

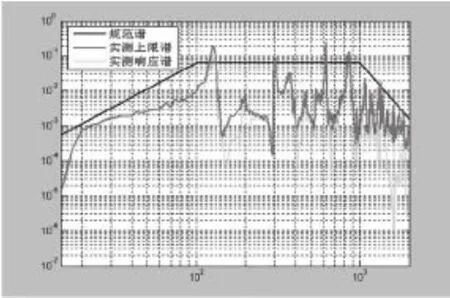
图7 界面处加速度试验条件

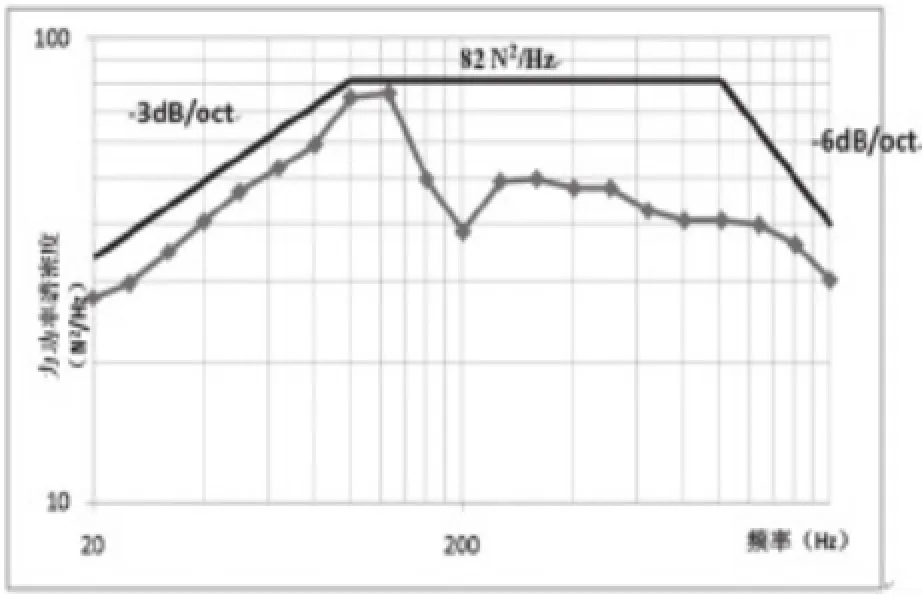
图8 随机振动试验中的力功率谱密度

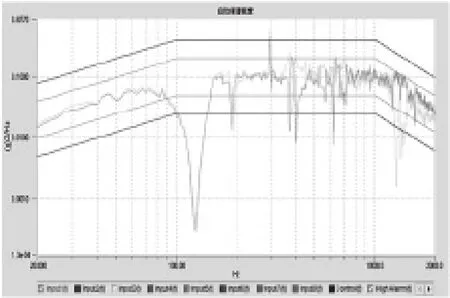
图9 加速度功率谱密度

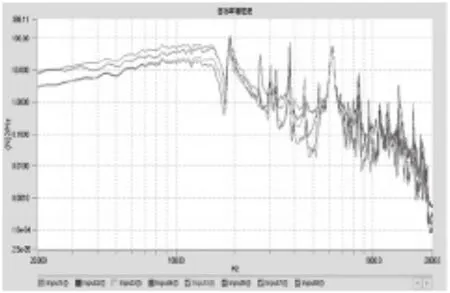
图10 界面力响应的功率谱密度

按照图2复杂二自由度方法计算力限试验条件实施程序来确定力试验条件。分析频段为20Hz～2000Hz，分析带宽为三分之一倍频程。对得到的曲线进行极值包络得到最终采用的力限试验条件，详见图8。

3.4.5 步骤5：验证力限试验的优势和有效性

试验采用的加速度试验条件与加速度控制振动试验相同，如图9所示。加入力限试验条件后，得到的界面加速度功率谱密度如图9所示。界面的力功率谱密度如图10所示。

由图9可以看出，由于力限制的介入，使得加速度输入功率谱密度在试件的第一阶固有频率和附近出现了明显下凹。

比较图10可以看出，在力限制作用下，力限控制试验将未加力限时本应出现在如图6中所示的所有高于力试验条件的峰值部分全部削掉，使试验界面力更趋于实际。在试件共振频率附近，力限控制试验的控制精度远好于加速度控制试验的控制精度，可以有效减轻产品过试验问题。

4 总结

本文通过理论分析和工程实践两个方面对力限控制试验技术展开研究。试验结果表明，力限控制试验是通过测量和限制振动台与试件界面的力，确保界面力不超过给定的力谱，从而避免实际振动试验中过试验问题。本论文的研究成果为今后开展力限试验研究工作具有一定借鉴意义，所进行的试验方法研究具有一定的实际运用价值。

[1] Spanos,P.D.,Gregory,L.,Davis,G.L. A perspective on the vibration overtest problem [J]. The Shock and vibration Digest,2001,33(3):177-186.

[2]黄波,张正平,李海波,任方. 力限振动试验技术进展综述[J]. 强度与环境 , 2012,12:18～27.

[3]齐晓军, 航天器振动试验控制技术研究[D]: [学位论文].长沙：国防科学技术大学, 2011.

[4]岳志勇,张俊刚,冯咬奇. 力限振动试验力谱确定方法[J]. 航天器环境工程, 2011(3).

游亚飞（1981.8-），女，硕士， 高工，从事环境与可靠性试验与研究工作。

Application and Research on Force Limited Vibration Testing Method

YOU Ya-fei, GAO Bao-yu, LI Guang-yuan, YU Xue-wu
（CAPE, Beijing 100028）

This paper introduces the reasons of overtesting in traditional vibration test. In addition, structural impedance characterization is introduced. It defines the apparent mass, the effective mass and the residual mass. Detailed calculations for force limitation specification are presented on the basis of the model of complex two degree of freedom method. Finally, taking the aluminium plate as the example, it establishes a typical force limited test project, and summarizes the method and procedure of the force limited control test. Thus the test result shows that the overtesting problem is solved by using the force limited control test method.

force limited; vibration; model of complex two degree of freedom method

V216.2+1

A

1004-7204（2014）06-0072-06