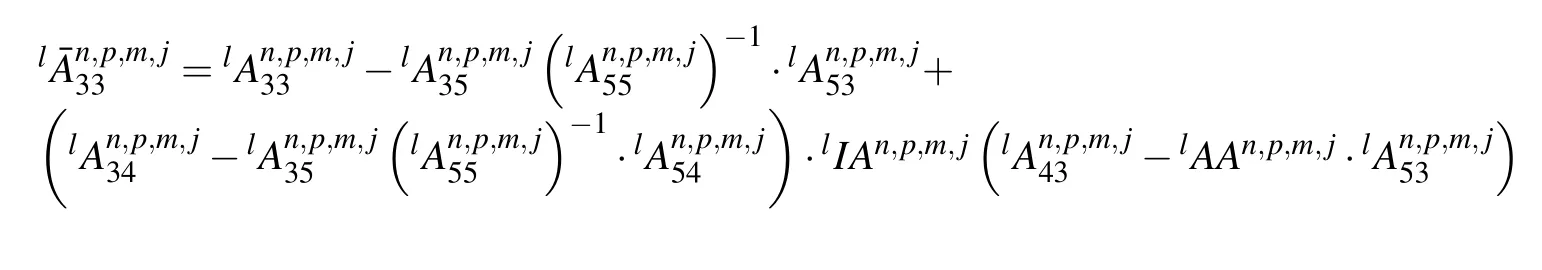Wave Propagation in Functionally Graded Piezoelectric-piezomagnetic Rectangular Rings

Yuchun DuanXiaoming ZhangYuqing Wang and Jiangong Yu

1 Introduction

With the increasing usage in various applications including sensors,actuators and storage devices piezoelectric-piezomagnetic composites(PPC)have received considerable research effort in the past ten years[Achenbach(2000);Sladek,Sladek,Solek and Atluri(2008);Bishay,Sladek,Sladek and Atluri(2012)].For the purpose of design and optimization of PPC transducers,wave propagation in various PPC attracted many researchers.

Cao[Cao,Shi and Jin(2012)]investigated Lamb waves propagating in the functionally graded piezoelectric-piezomagnetic material plate by employing the power series technique.Wei[Wei and Su(2006)]studied the axisymmetric flexural wave in PPC cylinders by using ‘bar model’.By virture of propagator matrix and state-vectorapproaches,Chen[Chen,Pan and Chen(2007)]presented an analyticaltreatment for the propagation of harmonic waves in PPC multilayered plates.Wu[Wu,Yu and He(2008)]used the orthogonal polynomial approach to investigate the wave propagating characteristics in the non-homogeneous magneto-electro-elastic plates.The polynomial approach was also applied to calculate the guided wave in imhomogeneous magneto-electro-elastic cylindrical plates[Yu and Wu(2009)]and spherical plates[Yu and Ma(2010);Xue,Pan and Zhang(2011)]proposed a simple nonlinear model to investigate the solitary waves in a magneto-electro-elastic circular bar based on the the Jacobi elliptic function expansion method.Using a self-adjoint method,the wave propagation in a magneto-electro-elastic square column was studied by Wei[Wei and Su(2008)].

Wave propagation in piezoelectric-piezomagnetic periodically layered structures received attentions[Liu,Wei and Fang(2010);Pang,Wang,Liu and Fang(2010);Zhao,Zhong and Pan(2012)]for analyzing the band gaps The penetration depth of the BleusteinGulyaev waves in a functionally graded transversely isotropic electromagneto-elastic half-space was discussed by Li[Li Jin and Qian(2013)].Sun[Sun,Ju,Pan and Li(2011)]and Nie[Nie,Liu,Fang and An(2012)]investigated the effects of the imperfect interface on the SH waves propagating in piezoelectricpiezomagnetic layered structures.The reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric-piezomagnetic media was discussed by Pang[Pang and Liu(2011)]By using Legendre and Laguerre polynomial approach,Matar[Matar,Gasmi,Zhou,Goueygou and Talbi(2013)]computed propagation constants and mode shapes of elastic waves in layered piezoelectricpiezomagnetic composites.The propagation of SH wave in the layered functionally gradient piezoelectric-piezomagnetic structure was studied by Singh[Singh and Rokne(2013)].

As a common structure,the ring ultrasonic transducer has been widely used in ocean engineering and medical fields.But few investigations on the wave propagation in ring transducers have been reported.This paper proposed a double orthogonal polynomial series approach to solve the wave propagation problem in a functionally graded piezoelectric-piezomagnetic(FGPP)ring with a rectangular cross section.Two material gradient directions(radial direction and axial direction)are respectively considered.The dispersion curves and the displacement profiles of various FGPP rectangular rings are presented and discussed.The investigating resultscan be used to directthe design and optimization ofthe ring FGPP transducers.In this paper,traction free and open circuit boundary conditions are assumed.

2 Mathematics and formulation of the problem

Considering an orthotropic ring with a rectangular cross-section in cylindrical coordinate(rθ,z),as shown in Figure.1.his height inzdirection anddis thickness inrdirection,anda,bdenote the inner and outer radius respectively.The radius to thickness ratio is defined asη=b/(b−a)and the width to height ratio isd/h.Its polarization direction is in therdirection.

Figure 1:Schematic diagram of a ring with rectangular cross section.

For the wave propagation considered in this paper,the body forces and electric charges and current densities are assumed to be zero.Thus,the dynamic equation for the ring is governed by

whereTij,ui,DiandBiare the stress,elastic displacement,electric displacement and magnetic induction components,respectively andρis the density of the material.In this study,quasi-magneto-electro-static assumptioin is made.

The relationships between the general strain and general displacement components can be expressed as

whereεij,EiandHiare the strain components,the electric field and the magnetic field;φandψare the electric potential and the magnetic potential components,respectively.

We introduce the function I(r,z)

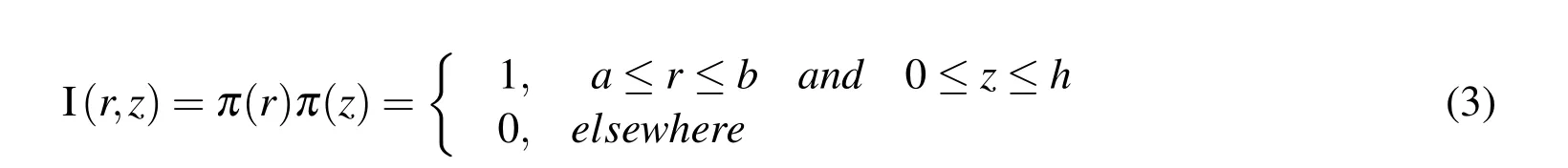
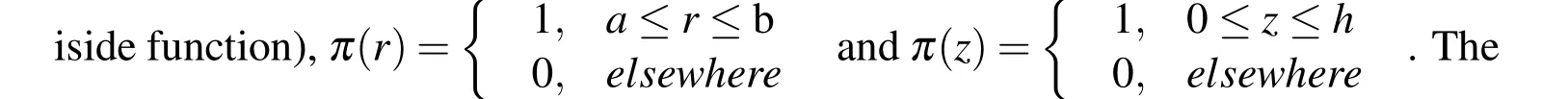
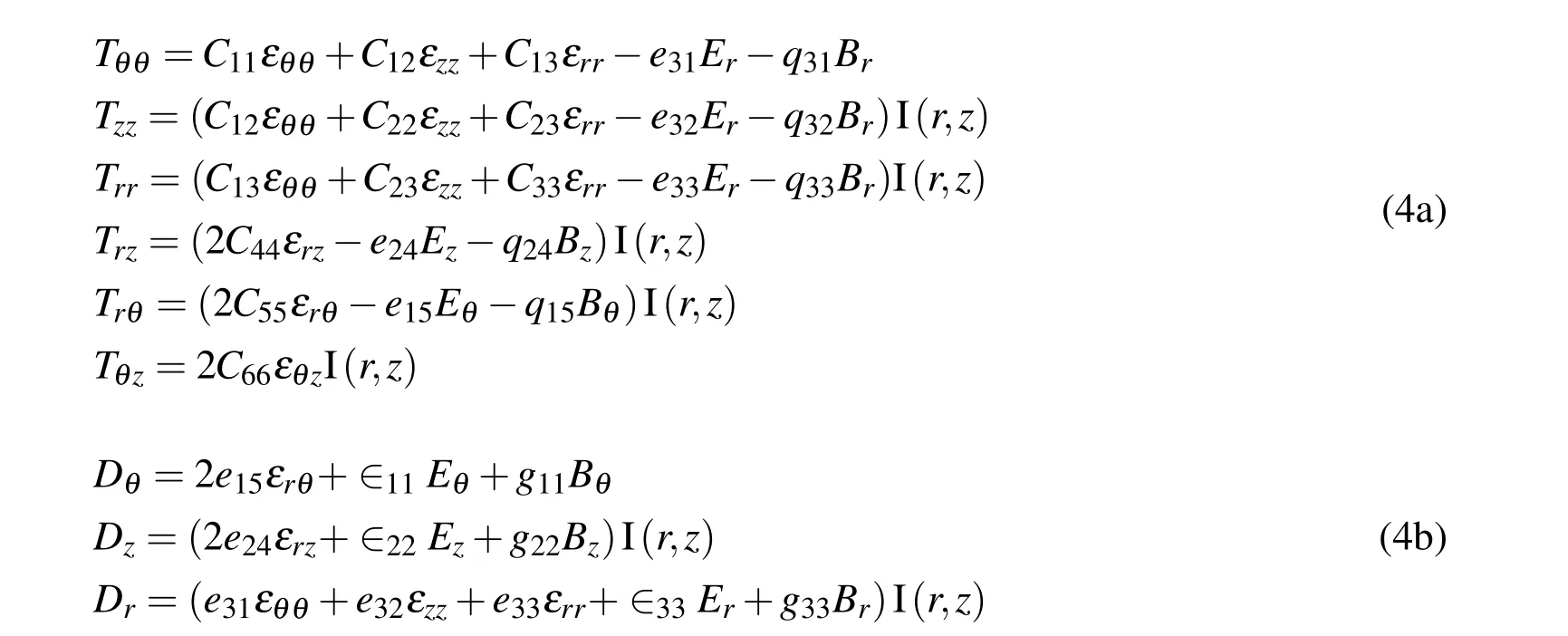
whereCij,eijandqijare the elastic,piezoelectric,and piezomagnetic coefficients respectively;∈ij,gij,andµijare the dielectric,magneto-electric,and magnetic permeability coefficients,respectively.

In this paper,we consider two different material gradient directions,namely,the radial direction and the axial direction.For FGPP rings that material properties vary in radial direction,we denote them byr-directional FGPP rings.For rings that t material properties vary in axial direction,we denote them bya-directional FGPP rings.For ar-directional FGPP ring,the elastic parameter is dependent onr,and can be fitted into the polynomial series of the radius

With implicit summation over repeated indices,Cij(r)can be written compactly as

And other material parameters can be treated in the same way,

For ana-directional FGPP ring,the material parameters are dependent onzand can be expressed as

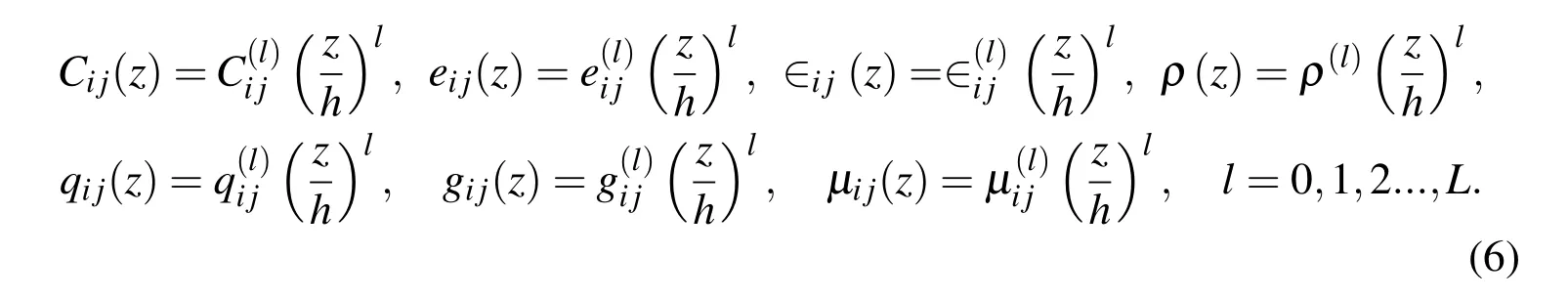
For a free harmonic wave propagating in the circumferential direction of a ring,we assume the displacement,electric potential and the magnetic potential components to be of the form

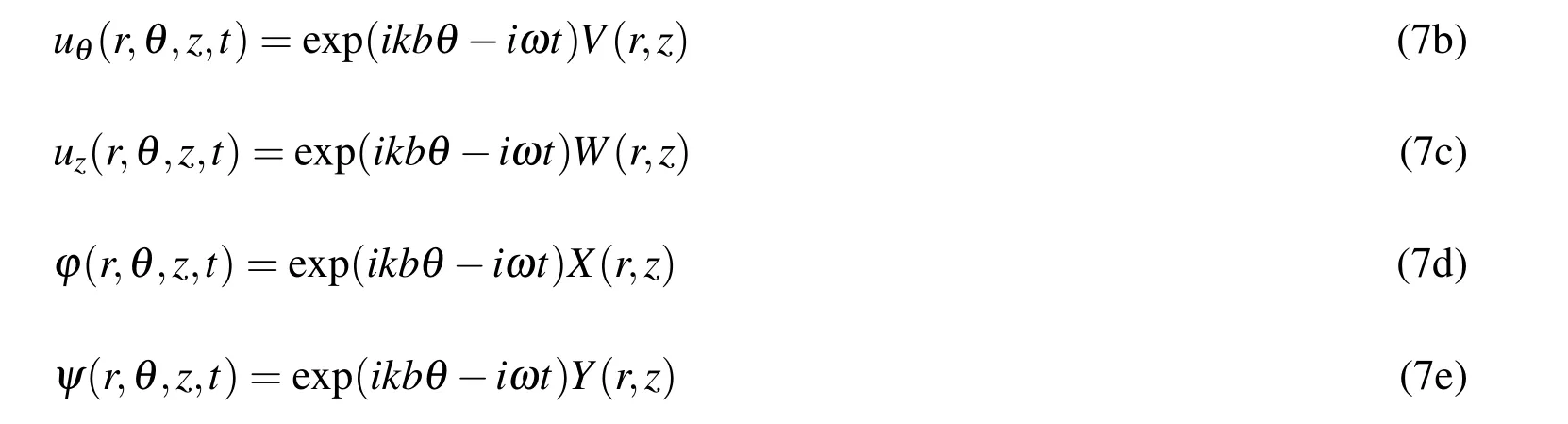
whereU(r,z),V(r,z)andW(r,z)represent the amplitude of vibration in ther,θ,zdirections respectively;X(r,z)andY(r,z)represent respectively the amplitudes of electric potential and magnetic potential.kis the magnitude of the wave vector in the propagation direction,andωis the angular frequency.

Substituting Eqs.(2),(3),(4),(5)/(6)and(7)into Eq.(1),the governing differential equations in terms of the displacement,electric potential and magnetic potential components can be obtained.Here,the case of ther-directional FGPP ring is given:

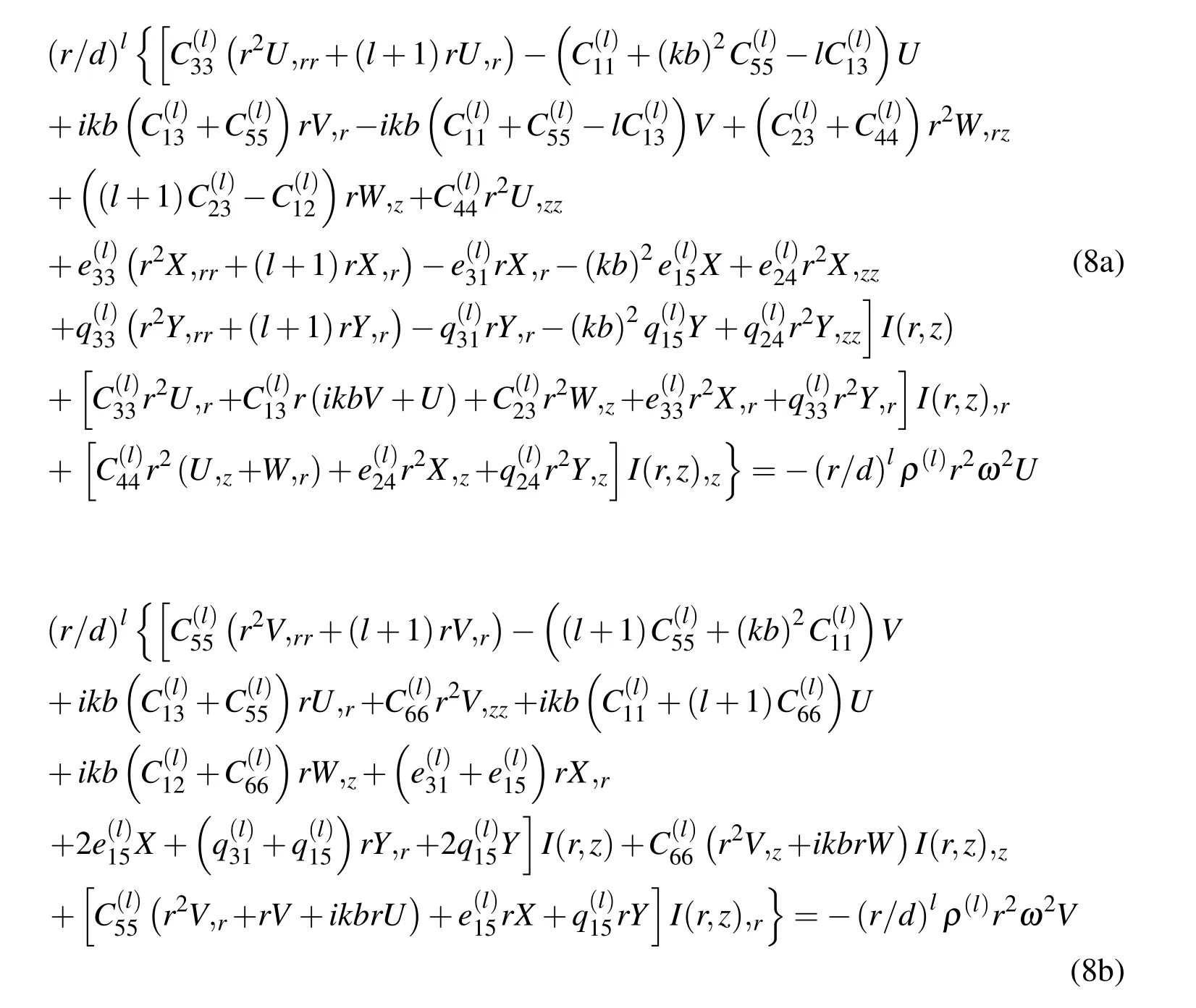
where a subscript comma indicates partial derivative.

To solve the coupled wave equations,U(r,z),V(r,z),W(r,z),X(r,z)andY(r,z)are expanded into products of two Legendre orthogonal polynomial series as

withPmandPjbeing themth and thejth Legendre polynomial.Theoretically,mandjrun from 0 to∞.However,in practice the summation over the polynomials in Eq.(9)can be truncated at some finite valuesm=Mandj=J,when the effects of higher order terms become negligible.

Multiplying each equation byQn(r)·Qp(z)·e−jωtwithnandprunning respectively from zero toMand zero toJ,and integrating overzfrom zero tohandrfromatoband taking advantage of the orthonormality of the polynomialsQm(r)andQj(z),Eq.(8)can be reorganized into a form of the system problem:

Substituting Eq.(12)into Eq.(11d),

Substituting Eq.(13)into Eq.(12),

Substituting Eq.(13)and(14)into Eq.(11a),(11b)and(11c),gives:

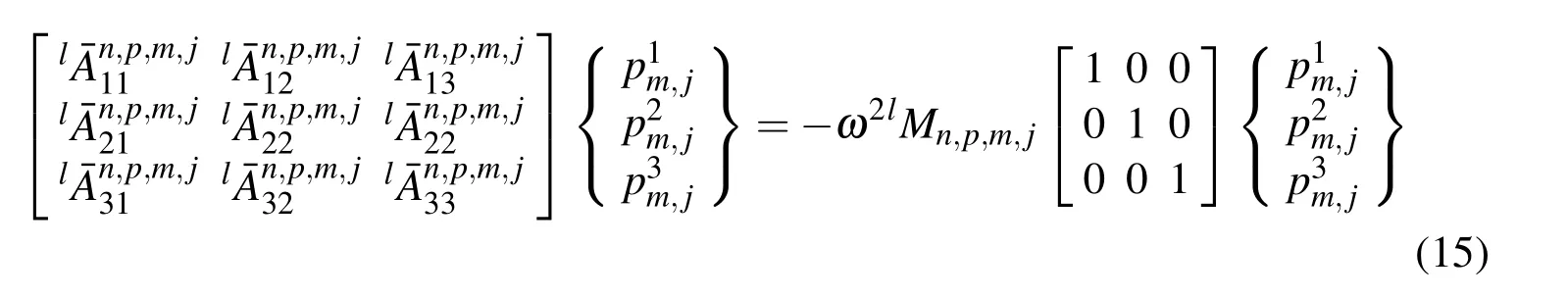
3 Numerical results and discussions

In order to calculate the effective parameters of the FGPP ring,the Voigt-type model is used in this study.For thea-directional FGPP rectangular ring,it can be expressed as

for ther-directional FGPP rectangular ring

whereVi(z)/Vi(r)andCidenote the volume fraction of theith material and the corresponding physical property of theith material,respectively,and∑Vi(z)=1/∑Vi(r)=1.So,the properties of the FGPP can be expressed as

According to Eq.(5)and(6),the gradient profile of the material volume fraction can be expressed as a power series expansion.The coefficients of the power series can be determined using the Mathematica function ‘Fit’.

Based on the above mathematical formulation,computer programs in terms of the proposed polynomial method have been written using Mathematica to calculate the dispersion curves and the displacement distributions for various FGPP rectangular rings.

3.1Comparison with the available solution from transfer matrix method

Because no reference results for the guided waves in FGPP or FG rectangular rings can be found in literature,we consider a homogeneous square steel ring with a very large radius to thickness ratioη=1000 to make a comparison with known results of a straight steel square bar from the semi-analytical finite element method[Hayashi,Song and Rose(2003)].For the steel square bar,CL=5.85 km/s,CT=3.23 km/s andh=d=5.08mm.Here,CLandCTare respectively the longitudinal and the transverse wave velocities.Figure 2 shows the corresponding dispersion curves,where dotted lines are from Hayashi[Hayashi,Song and Rose(2003)]and dashed lines are obtained from the present approach.As can be seen,the results from the polynomial approach agree well with the reference data,which verifies the correctness and the accuracy of the present method.

3.2Dispersion curves for FGPP rectangular rings

In this section,we take the Ba2TiO3CoFe2O4FGPP rectangular rings as examples to discuss the wave characteristics.The bottom surface for thea-directional FGPP rectangular ring and the inner surface for ther-directional FGPP rectangular ring are pure Ba2TiO3.The material parameters of the two materials with polarization in the thickness direction are given in Table 1.

Firstly,we consider four linely FGPP square rings(d/h=1):(a)a-directional FGPP ring withη=10;(b)r-directional FGPP ring withη=10;(c)a-directional FGPP ring withη=2;(d)r-directional FGPP ring withη=2.Their phase velocity dispersion curves are shown in Figure 3.It can be seen that the first two wave modes have no cut-off frequencies.This feature is different from that for an in finite FGPP flat plate,in which the first mode has no cut-off frequencies.In a flat plate,only the thickness direction is a finite dimension,but there are two finite dimensions in a rectangular ring.Furthermore,the radius to thickness ratio has a signi ficant effect on the dispersion curves.With the radius to thickness ratio increasing,the difference between the first mode and the second mode of the FGPP square ring becomes small at the low frequency.The reason is that the ring is more and more close to the square bar with the radius to thickness ratio increasing,and for the square bar,the first two modes is very similar due to the symmetry of the geometry and material distribution.For the FGPP ring with small radius to thickness ratio,the difference between the dispersion curves of thea-directional FGPP ring and the ones of ther-directional FGPP ring is more signi ficant,which results from two reasons:(1)the piezomagnetic effect and piezoelectric effect are different for the FGPP rings with different polarization directions.(2)For the linelyr-directional FGPP ring,the volume fraction of the outside material(CoFe2O4)is higher than that of the inside material(Ba2TiO3),and the difference between the two volume fractions become larger with the radius to thickness ratio decreasing,so that the difference of the strength of the piezomagnetic effect and piezoelectric effect is more notable.

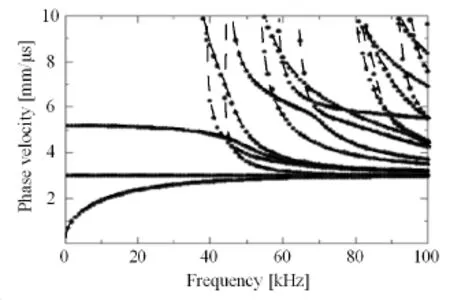
Figure 2:Phase velocity dispersion curves of the square steel rod;dotted lines:Hayashi’s results,dashed lines:authors’results.

Table 1: The material properties of the two materials(Cij(109N/m2),∈ij(10−10F/m2),eij(C/m),qij(N/Am),µij(10−6Ns2/C2),ρ(103kg/m3)).

Figure 3:Phase velocity dispersion curves for the FGPP square rings(black lines,a-directional FGPP ring;red lines,r-directional FGPP ring):(a)η=10,(b)η=2.

The cross section of the above four FGPP rings is square.Next,two linely FGPP rectangularringswithη=10 are considered:(e)r-directionalFGPP ring withd/h=0.5;(f)a-directional FGPP ring withd/h=2 Figure 4 shows the corresponding phase velocity dispersion curves.We can see that the width to height ratio can also influence the dispersion curves signi ficantly.

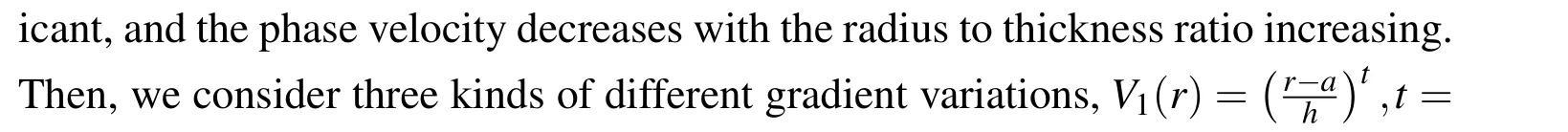
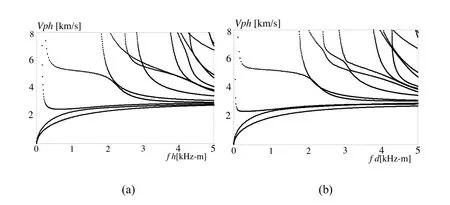
Figure 4:Phase velocity dispersion curves for FGPP rectangular rings:(a)rdirectional FGPP ring with d/h=0.5,(b)a-directional FGPP ring with d/h=2.

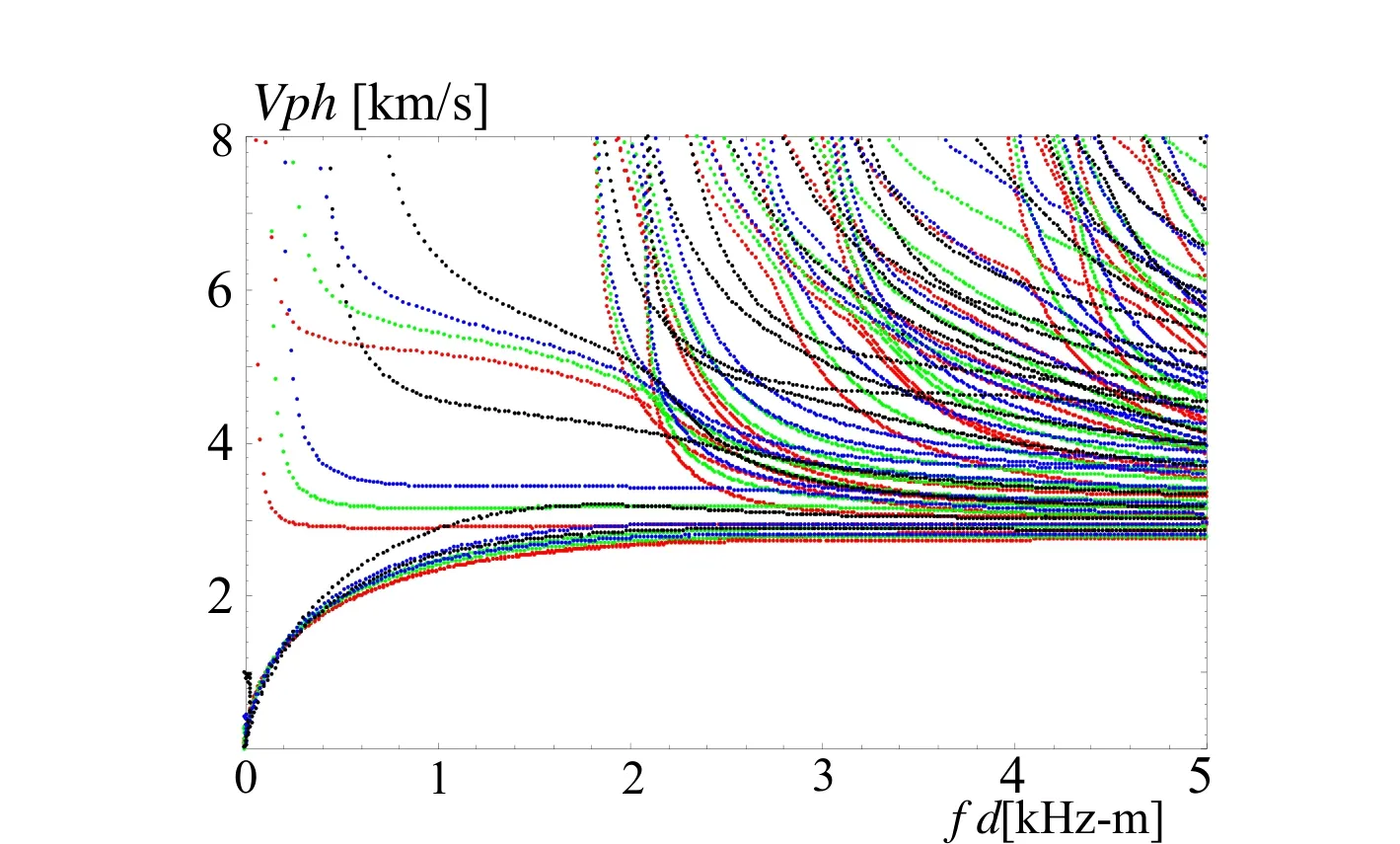
Figure 5:Phase velocity dispersion curves for a-directional FGPP square rings with different radius to thickness ratios:red lines,η=10;green lines,η=5;blue lines,η=3.5;black lines,η=2.

Figure 6:Phase velocity dispersion curves for a-directional FGPP square rings with different gradient variations with η=10(red lines,linearly gradient variation;blue lines,squarely gradient variation;black lines,cubically gradient variation):(a)mode 1-3;(b)mode 4.

The above three gradient fields are monotonic.Next,a cosinusoidally FGPP ring and a sinusoidally FGPP ring withη=10 andd/h=1 are considered.The corresponding phase velocity dispersion curves are given in Figure 7.We can see that the dispersion characteristics are different for the two FGPP square rings with different gradient fields.

3.3Displacement shapes

In this section,we discuss the wave characteristics through the mechanical displacement profiles.Figures.8 and 9 illustrate the displacement shapes of the second and fifth modes for a linearlya-directional FGPP square ring atkd=180.We can see that most displacements distribute near the bottom edge,namely,the side with more Ba2TiO3.The reason lies in that the body wave speed of Ba2TiO3is lower than that of CoFe2O4.Figures.10 and 11 show the case for a cosinusoidallya-directional FGPP square ring.We can see that that the displacement mostly distribute around the bottom and top sides.That means they mostly distribute aroundz=0 andz=1,where the volume fraction of Ba2TiO3is higher.This phenomenon shows the high frequency wave always propagate on the side with more materials of high wave speed.So,through changing the gradient variation of the FGPP ring,we can to obtain any field distributions that we want.Furthermore,in figures 10 and 11,the displacementwis symmetric and displacementuandvare antisymmetric with respect to thez-axis,which results from the material volume fraction are symmetrically distributed on thez-axis.

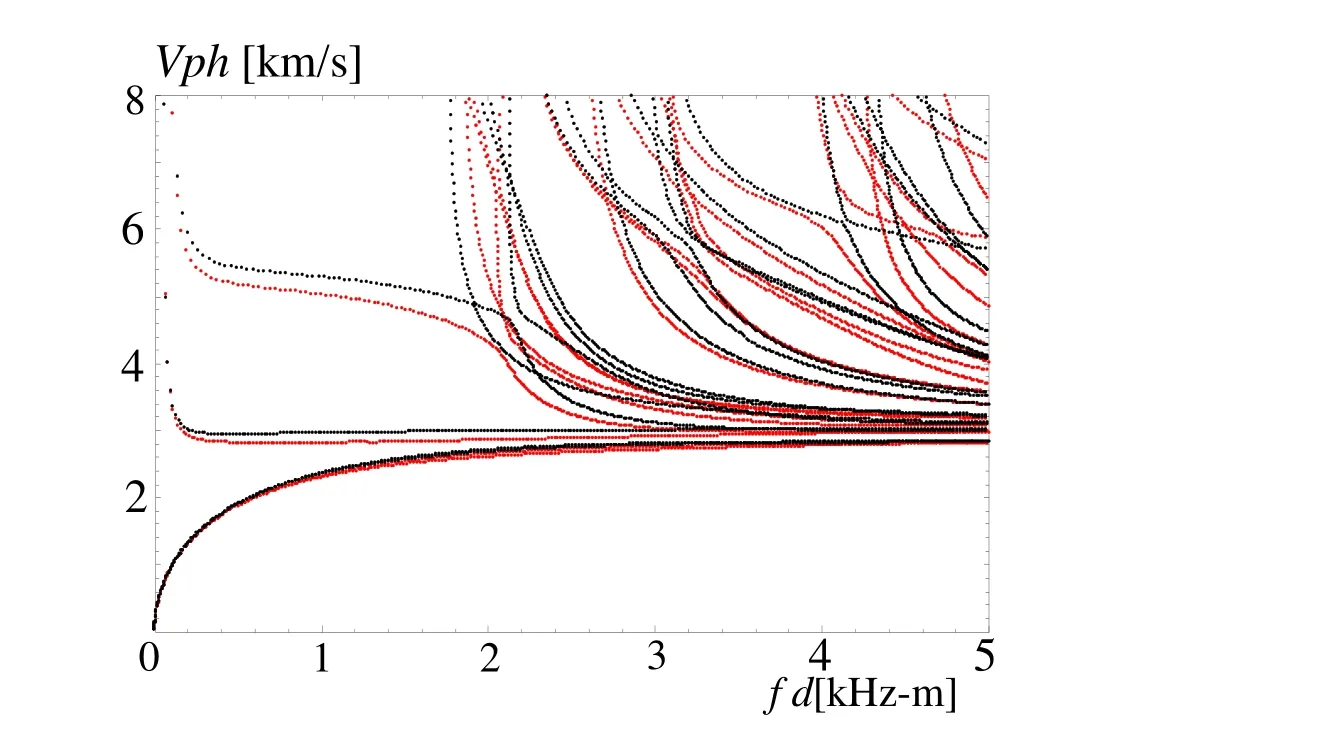
Figure 7:Phase velocity dispersion curves for a-directional FGPP square rings with differentgradientvariationswithη=10(red lines,cosinusoidally gradientvariation;black lines,sinusoidally gradient variation).

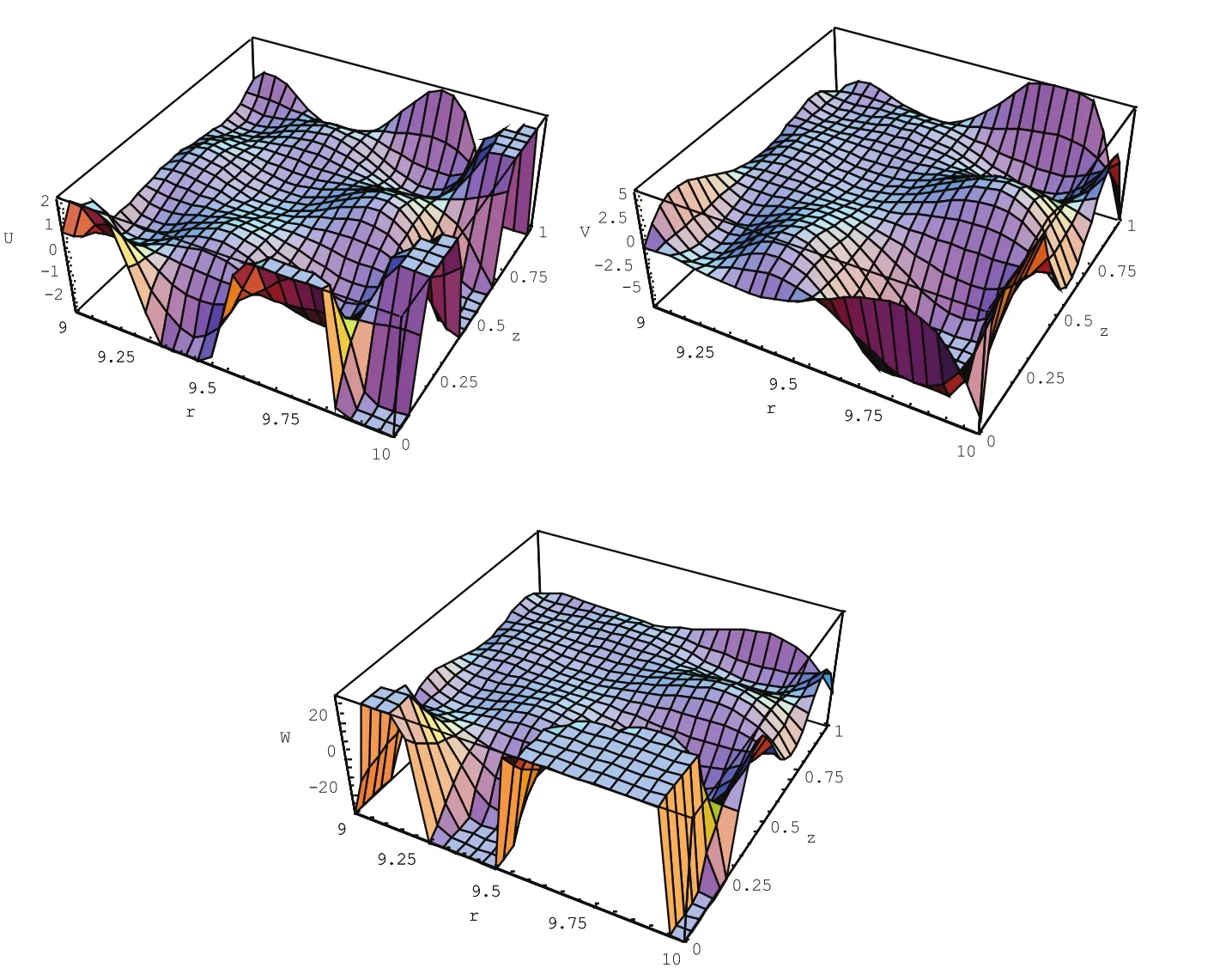
Figure 8:Displacement profiles of the second mode for the linearly a-directional FGPP square ring at kd=180.

Figure 9:Displacement profiles of the fifth mode for the linearly a-directional FGPP square ring at kd=180.

Figure 10:Displacement profiles of the second mode for the cosinusoidally adirectional FGPP square ring at kd=180.

Figure 11:Displacement profiles of the fifth mode for the cosinusoidally adirectional FGPP square ring at kd=180.

4 Conclusions

In this paper,wave propagation analysis of a 2-D FGPP rectangular ring is solved by a double orthogonal polynomial series approach.The dispersion curves and displacement distributions of various FGPP rectangular rings are presented and discussed.According to the numerical results,we can draw the following conclusions:(a)Numerical comparison of the dispersion curves with reference solutions shows that the double orthogonal polynomial method is appropriate to solve the guided wave propagation problem in 2-D FGPP structures.

(b)The radius to thickness ratio and the width to height ratio and the gradient field all have significant influences on the guided wave charateristics.

(c)High frequency waves propagate predominantly around the side with more material having lower wave speed.

So,through changing the radius to thickness ratio,the width to height ratio and the gradient variation of the FGPP ring,we can obtain the ring transducers with the dispersion features and field distributions that we want.

Acknowledgement:The work was supported by the National Natural Science Foundation ofChina(No.11272115)and the ExcellentYouth Foundation ofHe’nan Scientific Committee of China(No.144100510016)and Foundation for Distinguished Young Scholars of Henan Polytechnic University(No.J2013-08)and Research Fund forthe DoctoralProgram ofHenan Polytechnic University(No.B2009-81).

Achenbach,J.D.(2000):Quantitative nondestructive evaluation.International Journal of Solids and Structures,vol.37,pp.1327.

Bishay,P.L.;Sladek,J.;Sladek,V.;Atluri,S.N.(2012):Analysis of Functionally Graded Magneto-Electro-Elastic Composites Using Hybrid/Mixed Finite Elements and Node-Wise Material Properties.CmcComputers Materials&Continua,vol.29,no.3,pp.213261

Cao,X.S.;Shi,J.P.;Jin,F.(2012):Lamb wave propagation in the functionally graded piezoelectric-piezomagnetic material plate.Acta Mechanica,vol.233,no.5,pp.10811091

Chen,J.Y.;Pan,E.;Chen,H.L.(2007):Wave propagation in magneto-electroelastic multilayered plates.International Journal of Solids and Structures,vol.44,pp.10731085.

Datta,S.;Hunsinger,B.J.(1978):Analysis of surface waves using orthogonal functions.J.Appl.Phys,vol.9,no.2,pp.75479.

Hayashi,T.;Song,W.J.;Rose,J.L.(2003):Guided wave dispersion curves for a bar with an arbitrary cross-section,a rod and rail example.Ultrasonics,vol.41,no.3,pp.175-183.

Li,P.;Jin,F.;Qian,Z.(2013):Propagation of the BleusteinGulyaev waves in a functionally graded transversely isotropic electro-magneto-elastic half-space.European Journal of Mechanics-A/Solids,vol.37,pp.1723.

Liu,J.;Wei,W.;Fang,D.(2010):Propagation behaviors ofshear horizontal waves in piezoelectric-piezomagnetic periodically layered structures.Acta Mechanica Solida Sinica,vol.23,no.1,pp.77-84.

Matar,O.B.;Gasmi,N.;Zhou,H.;Goueygou,M.;Talbi,A.(2013):Legendre and Laguerre polynomial approach for modeling of wave propagation in layered magneto-electro-elastic media.The Journal of the Acoustical Society of America,vol.133,no.3,pp.14151424.

Nie,G.Q.;Liu,J.X.;Fang,X.Q.;An,Z.J.(2012):Shear horizontal(SH)waves propagating in piezoelectricpiezomagnetic bilayer system with an imperfect interface.Acta Mechanica,vol.223,no.9,pp.19992009.

Pang,Y.;Liu J.X.(2011):Reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric and piezomagnetic media.European Journal of Mechanics-A/Solids,vol.30,no.5,pp.31740.

Pang,Y.;Wang,Y.S.;Liu,J.X.;Fang,D.N.(2010):A study of the band structures of elastic wave propagating in piezoelectric/piezomagnetic layered periodic structures.Smart Materials and Structures,vol.19,no.5,pp.055012.

Singh,B.M.;Rokne,J.(2013):Propagation of SH waves in layered functionally gradient piezoelectric-piezomagnetic structures.Philosophical Magazine,vol.93,no.14,pp.16901700.

Sladek,J.;Sladek,V.;Solek,P.;Atluri,S.N.(2008):Modeling of intelligent material systems by the MLPG.CmesComputer Modeling in Engineering&Sciences,vol.34,no.3,pp.273-300.

Sun,W.H.;Ju,G.L.;Pan,J.W.;Li Y.D.(2011):Effects of the imperfect interface and piezoelectric/piezomagnetic stiffening on the SH wave in a multiferroic composite.Ultrasonics,vol.51,no.7,pp.831838.

Wei,J.;Su,X.Y.(2006):Wave Propagation and Energy Transportation along Cylindrical Piezoelectric Piezomagnetic Material.Acta Scientiarum Naturalium Universitatis Pekinensis,vol.42,pp.310314

Wei J.P.;Su X.Y.(2008):Steady-state Response of the Wave Propagation in a Magneto-Electro-Elastic Square Column.CmesComputer Modeling in Engineering&Sciences,vol.37,no.1,pp.65-84

Wu,B.;Yu,J.G.;He,C.F.(2008):Wave propagation in non-homogeneous magneto-electro-elastic plates.Journal of sound and vibration,vol.317,pp.250-264.

Xue,C.X.;Pan E.;Zhang S.Y.(2011):Solitary waves in a magneto-electroelastic circular bar.Smart Materials and Structures,vol.20,no.10,pp.105010.

Yu,J.G.;Wu,B.(2009):Circumferential wave in magneto-electro-elastic functionally graded cylindrical curved plates.European Journal of Mechanics A/Solids,vol.28,no.3,pp.560-568

Yu,J.G.;Ma Q.J.(2010):Wave characteristics in magneto-electro-elastic functionally graded spherical curved plates.Mechanics of Advanced Materials and Structures,vol.17 no.4,pp.287-301.

Zhao,J.;Zhong,Z.;Pan,Y.(2012):Theoretical study of SH-wave propagation in piezoelectric/piezomagnetic layered periodic structures.The Journal of the Acoustical Society of America,vol.131,no.4,pp.3327-3327.

Appendix

The elements of the matrices in Eq.(15)are given by