基于叠加修正法的承弯组合结构临界预紧力研究

董晓传，金淼，张杰，姚阳

(燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛，066004)

承弯组合结构作为预紧组合结构的一种，是指预紧力作用在纵向方向，并且承受横向载荷的组合结构，通常作为主要的承力部件广泛应用于锻压成形设备、加工机床及模具等方面[1-3]。整体性是承弯组合结构的一个关键问题[4]。所谓整体性，是指通过预紧连接在一起的各部分结构，始终能够保持一个整体，不出现开缝现象[5-6]。因为一旦出现开缝，在反复的加载与卸载过程中，频繁的撞击极易引起开缝处发生局部塑形变形或破坏，进而导致整个结构失效。预紧力是保证整体性的关键因素，然而，如何确定合理的承弯组合结构预紧力始终是设计过程中的难题。吴生富等[7]提出用神经网络取代有限元对承弯组合结构进行整体性分析，提高了计算效率及计算精度，但其并未涉及组合结构预紧力的计算方法。文献[8]通过力矩平衡，提出了中心载荷工况下液压机下横梁拉杆预紧力的求解方法。文献[9]在其基础上研究了扩孔工况下组合下横梁拉杆的受力及尺寸。然而这些计算方法均基于材料力学中的弯曲变形原理，未考虑组合结构的剪切变形。承弯组合结构限于结构刚度、载荷工况等因素的制约，其跨高比通常不大于3，属于深梁结构[10]。有别于欧拉-伯努利(Euler-Bernoulli)梁，深梁结构场量计算中不能忽略剪切变形的影响[11-12]。目前，在承弯组合结构预紧力的计算中考虑剪切变形的研究尚无报道。本文作者以矩形截面承弯组合结构为研究对象，为兼顾剪切变形，基于叠加修正法改进Airy 应力函数的求解结果，进一步提高组合结构x 方向应力场的计算精度，进而求解合理的承弯组合结构的临界预紧力。

1 承弯组合结构临界预紧力理论计算模型

承弯组合结构的二维结构简图如图1 所示。当承受中心载荷时，由于底部支座的支撑，组合结构承弯并产生一定的弯曲变形，导致子结构结合面出现分离趋势，而两端面处拉杆的预紧力可降低开缝趋势，从而保证组合结构的整体性。

图1 承弯组合结构简图Fig.1 Sketch of pre-stressed composite beam

为简化承弯组合结构预紧力的计算，此处提出3条假设：

1) 开缝前，按照整体结构计算组合结构的各种场量关系；

2) 承弯组合结构变形前后拉杆受力不变；

3) 所有作用力均为均布载荷。

提出假设1)的原因是：组合结构各子结构间若要紧密贴合，则其接触面处的x 方向应力必然为非正值，即压应力。因此，在开缝前，组合结构接触面处的应力场与相同尺寸及边界条件的整体结构应力场分布基本一致。提出假设2)的原因是：由于矩形截面组合结构刚度远大于拉杆刚度，且承载后拉杆变形量微小。

根据上述假设，建立承弯组合结构预紧力的平面应变理论计算模型，如图2 所示。图中，q 为外加载荷的集度，q0为预紧力的集度，a 为外加载荷在单个子结构的作用区间，b 为支撑载荷在单个子结构的作用区间，c 为组合结构高度的1/2，c1为组合结构x 轴距上拉杆中心线的距离，c2为组合结构x 轴距下拉杆中心线的距离，d 为预紧力的作用区间，l 为支撑载荷作用中心距的1/2，l0为单个子结构的长度。

图2 组合结构预紧力计算模型Fig.2 Theoretical model of composite structure

由图2 可知：加载后，模型必然产生一定的弯曲变形，根据弯曲特点，模型中截面下部的压应力逐渐减小，且最小值点位于接触面最下端M 点处。当该点压应力恰好为零时，该模型即成为组合结构临界预紧力计算模型，此时模型的状态称为临界开缝状态。因此承弯组合结构临界开缝判据可表示为

而其加载前的预紧力称为该载荷下承弯组合结构的临界预紧力。

图2 中的所有参数仅拉杆预紧力q0未知，因此，只需求出组合结构中截面处x 方向应力σx的表达式，再结合临界开缝判据式(1)，即可进行求解。

2 x 方向应力场的叠加修正解及临界预紧力计算

根据叠加原理可知，图2 中的理论计算模型可视为承受横向载荷的弯曲模型与承受纵向载荷的压缩模型2 部分的叠加。考虑到剪切变形，采用弹性力学中的Airy 应力函数求解该模型。

2.1 承弯组合结构x 方向应力场

图3 所示为理论模型的分解。图3(a)中弯曲模型仅在上、下表面受到非连续均布载荷的作用，且关于y 轴对称，将其按照周期为2l0的傅里叶三角级数形式展开，并进一步分解为一系列余弦函数模型与1 个均布载荷模型的叠加，分解模型的载荷在上、下表面的表达式如下。

余弦函数模型中，在y = ±c处，上、下表面的应力边界条件分别为

从而，可设如下形式Airy 应力函数：

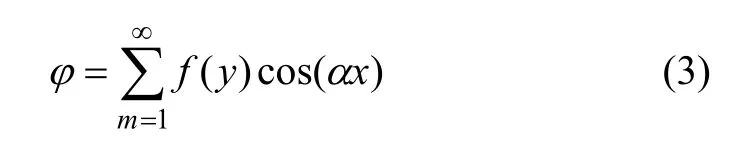
其中：f(y)为坐标y 的函数。将式(3)代入双调和方程，得到关于f(y)的常系数线性微分方程，求其通解可得f(y)的表达式，且含有4 个待定系数。再结合该部分上下表面的4 个应力边界条件，易于求得f(y)，再将其代入式(3)，从而可得余弦函数模型x 方向应力为

图3 理论模型的分解Fig.3 Decomposition of theoretical model

式中：

均布载荷模型中，结构在上、下表面受大小相等方向相反的均布载荷作用，易于求得其x 方向应力为零，因此，弯曲模型的x 方向应力只与式(4)有关。

同理，图3(b)中的压缩模型载荷可按照周期为2c的傅里叶三角级数形式展开，并进一步分解为一系列正弦函数模型、一系列余弦函数模型与一个均布载荷模型的叠加(坐标轴顺时针旋转90°)，其在两端面的表达式如下。

均布载荷模型：

正弦函数模型：

余弦函数模型：

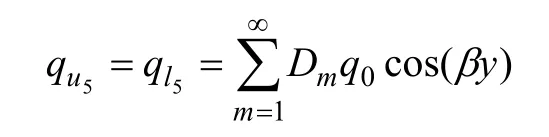
与弯曲模型计算方法相似，同理可求得其x 方向应力为

式中：

从而可知，式(4)与式(5)相加即为承弯组合结构x方向总的应力场：

2.2 叠加修正法

观察式(6)可知：由于在计算式(4)与式(5)时，未能考虑理论模型四边所有的边界条件，因此该结果不是模型的精确解。

通过上述分析可知，式(6)的误差主要源于式(4)，此处采用叠加修正法对式(4)进行适当修正，以提高承弯组合结构x 方向应力的计算精度。

所谓的叠加修正法是指将模型端部误差反向叠加至原理论解，使其满足该端部的边界条件。由于本文仅需精确求解x 方向应力，因此，该修正方法对y 方向应力的影响忽略不计。

由式(4)可知：当x=±l0时，弯曲模型x 方向应力为

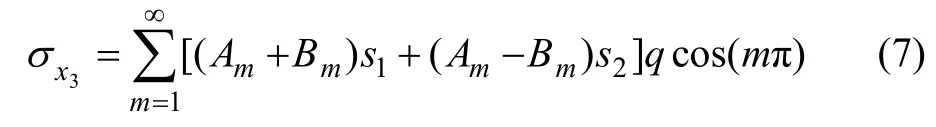
此亦为弯曲模型端部误差，将该误差的相反数叠加至式(4)并取x=0，则修正后的弯曲模型中截面x方向应力为

此处以跨高比为1，支撑长度和施力长度分别为300 mm 和500 mm 的整体结构为例，在承受20 MN的载荷工况下，其中截面x 方向应力的叠加修正解与有限元模拟解的对比如图4 所示。

由图4 可知：按照叠加修正法计算的弯曲模型理论解与相应的有限元计算结果重合度较高，相对误差较小。

图4 中截面x 方向应力的修正理论解与有限元解的对比Fig.4 Comparison of refined theoretical results and FEM results of stress along x direction in middle section

2.3 临界预紧力的计算

将式(8)与式(5)相加(取x=0)，从而得到整个承弯组合结构中截面x 方向应力的表达式为

再根据临界开缝判据式(1)，带入M 点的坐标值，表达式中仅含有未知数q0，从而可解得承弯组合结构的临界预紧力集度为

式中：下标M 表示带入点M 坐标值后的相应表达式。

3 实验验证

按照承弯组合结构临界预紧力的理论计算模型，设计并制造了矩形截面组合结构的实验装置。该装置支座可拆卸，变换位置后，可构成跨高比分别为1.0，1.5，2.0 和2.5 的组合框架。

实验中的外载荷、拉杆拉力及组合结构的接触状态均通过电测法测试，并通过德国IMC 数据采集系统实时采集记录各项数据。监测组合结构开缝状态的应变片位于子结构下表面靠近接触面一侧的中间位置(最易开缝处)。液压加载装置所加载荷则通过力传感器控制。

实验开始后，设置组合结构跨高比，然后施加一定的预紧力将两部分子结构预紧为一体，再启动液压加载装置，施加20 kN 载荷，观察组合结构接触面监测位置的应变数值。若应变值为零或接近为零，则此时的预紧力就是相应载荷下的临界预紧力，反之，则需根据应变数值适当调整拉杆的预紧力，直至满足临界开缝判据。之后分别施加载荷至30，40，50 和60 kN，测试不同载荷情况下所对应的临界预紧力数值。再调整支座位置，依次更换其余三组跨高比，重复上述实验过程，测试不同跨高比下，相应载荷对应的临界预紧力。实验所测结果与理论公式计算结果的对比，如图5 所示。

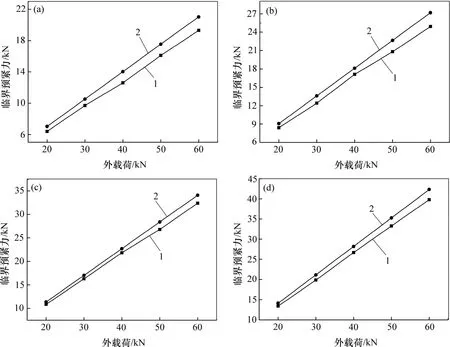
图5 不同跨高比下临界预紧力实验值与理论值对比Fig.5 Comparison of theoretical and experimental results under different span-depth ratios

由图5 可知：在同一跨高比下，当载荷变化时，随着载荷的增大，临界预紧力的数值均随之增大，且载荷与临界预紧力大致呈线性关系；当载荷不变，跨高比变化时，随着跨高比的增大，临界预紧力数值也有所增大。当跨高比由1.0 增加到2.5 时，临界预紧力理论值增大了约1 倍(不同载荷增大倍数相差不大)。

在相同跨高比和载荷条件下，组合结构临界预紧力的理论值均较实验值大。究其原因，误差主要源于本文的3 条假设。一方面，在理论计算中，将组合结构作为整体结构进行计算，势必导致接触面处较实际更难于出现开缝；另一方面，结构承载后发生弯曲变形，上、下拉杆受力必然发生变化，上拉杆拉力变小，下拉杆拉力增大，且下拉杆拉力增大幅度大于上拉杆拉力减小幅度(因组合结构弯曲中性层靠近模型底端)，而理论解相当于变形后上、下拉杆拉力的平均值。后者也是导致随着载荷的增大，实验值与理论值的误差有所增大的原因。在4 个不同跨高比下，实验值与理论值的最小误差为4.0%，最大误差为9.8%。

综上所述，叠加修正法得到的承弯组合结构临界预紧力计算公式理论值与实验值的相对误差均在10%以内，能够保证承弯组合结构的整体性。

4 结论

1) 建立了矩形截面承弯组合结构临界预紧力的理论计算模型，针对Airy 应力函数计算产生的误差，提出采用叠加修正法计算组合结构x 方向应力场。

2) 结合开缝判据公式，得到了承弯组合结构临界预紧力的理论计算公式。实验结果表明，基于叠加修正法得到的临界预紧力理论值与相应的实验值吻合较好，能够满足承弯组合结构的整体性要求。

[1] 聂绍珉. 现代大中型锻造液压机的特点及发展趋势[J]. 金属加工,2008(23)：20-23.NIE Shaomin. The characteristics and the development trends of large forging hydraulic press[J]. Metal Forming, 2008(23)：20-23.

[2] Hwang Y K, Lee C M. Development of automatic variable preload device for spindle bearing by using centrifugal force[J].International Journal of Machine Tools&Manufacture,2009,49：781-787.

[3] 杨家旺, 黄明辉, 陆新江, 等. 大型模锻压机极低速非线性摩擦建模与验证[J]. 中南大学学报(自然科学版),2013,44(12)：4841-4846.YANG Jiawang, HUANG Minghui, LU Xinjiang, et al.Nonlinear friction modeling and experimental verification for large die-forging hydraulic press under extremely low speed[J].Journal of Central South University (Science and Technology),2013,44(12)：4841-4846.

[4] 金淼, 董晓传, 邹宗园, 等. 给定预紧力下组合机架的上限载荷的计算[J]. 中国机械工程,2012,23(20)：2476-2480.JIN Miao, DONG Xiaochuan, ZOU Zongyuan, et al.Calculation of the upper-bound load for composite frame hydraulic press under the given preload[J].China Mechanical Engineering,2012,23(20)：2476-2480.

[5] 何敏, 孙智. 基于接触理论的高速精密压力机预紧力研究[J].机械工程学报,2010,46(11)：165-171.HE Min, SUN Zhi. Research on pre-tightened loads of the high-speed precision press with contact theory[J]. Journal of Mechanical Engineering,2010,46(11)：165-171.

[6] Strano M, Monno M,Rossi A.Optimized design of press frames with respect to energy efficiency[J]. Journal of Cleaner Production,2013,41：140-149.

[7] 吴生富, 聂绍珉, 金淼, 等. 大型组合结构整体性分析的人工神经网络模型[J]. 塑形工程学报,2007,14(2)：77-79.WU Shengfu, NIE Shaomin, JIN Miao, et al. Artificial neural network model of the unity of analysis of large composite structure[J]. Journal of Plasticity Engineering, 2007, 14(2)：77-79.

[8] 俞新陆. 液压机现代设计理论[M]. 北京： 机械工业出版社,2009：159-160.YU Xinlu. Modern design theories of hydraulic press[M].Beijing：China Machine Press,2009：159-160.

[9] 李龙, 王艳红, 胡晓龙. 液压机组合下横梁的连接螺栓组的设计计算[J]. 机械工程师,2010(9)：57-58.LI Long,WANG Yanhong,HU Xiaolong.Calculation and design of connecting bolts for combined lower beam of hydraulic forging press[J].Mechanical Engineer,2010(9)：57-58.

[10] Mohammad M, Mohd Z, Mohammad J. Experimental investigation to compare the modulus of rupture in high strength self compacting concrete deep beams and high strength concrete normal beams[J]. Construction and Building Materials, 2012,30(5)：265-273.

[11] YANG Lianzhi, SHANG Lange, GAO Yang. Further study on the refined theory of rectangle deep beams[J]. Acta Mechanica,2013,224(9)：1999-2007.

[12] 刘计良, 王正中, 陈立杰, 等. 均布载荷作用下悬臂深梁应力计算方法[J]. 清华大学学报(自然科学版), 2010, 50(2)：316-320.LIU Jiliang, WANG Zhenzhong, CHEN Lijie, et al. Stress calculation method for a cantilever deep beam subjected to a uniform load[J]. Journal of Tsinghua University (Science and Technology),2010,50(2)：316-320.