混流式机组负荷机架振动评价探析

曹登峰，潘罗平，周 叶，夏 伟

（中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038）

混流式机组负荷机架振动评价探析

曹登峰，潘罗平，周 叶，夏 伟

（中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038）

水电机组振动水平是表征机组运行稳定性的主要指标之一。本文以混流式机组负荷机架振动为例，通过研究相似机组负荷机架在动静荷载作用下的振动特性，提出了一个表征动静荷载关系比的无量纲参数。根据相似水力条件引起的机组振动所导致的相对功率损耗一致的假定，运用最小二乘原理，建立了机组单位转速与该振动参数的回归模型，进而以不同的置信水平划分了不同的振动区域，对振动水平进行评价，并提出了建议措施。成果表明利用该方法评价负荷机架振动水平是有效且可行的。

混流式机组；负荷机架振动；振动建模；最小二乘原理；振动评价

1 研究背景

水电站在电网中承担着调峰、调频、调相和事故备用的作用，其运行安全直接关系到电网的安全稳定，一旦发生事故，将会带来重大的经济损失和严重的社会影响。水电机组作为水电站的核心设备，其运行稳定性对水电站的运行安全至关重要［1］。机组的振动水平是表征机组运行稳定性的主要指标之一，它能直接反映出机组的运行状态，并蕴含着可能的故障征兆。当机组振动超过一定限值时，将严重影响机组的安全稳定。对机组的振动进行监测和分析，并对振动等级水平进行评价，是保障机组安全稳定运行的重要手段，也是进一步开展水电机组故障诊断和状态检修的必要前提［2］。

最早且比较完整的水电机组振动评价标准由赖斯朋于1939年提出，该评价方法将允许振动值作为振动频率的函数，根据由频率确立的振动范围评价振动水平［3］。前苏联工程师伏拉基斯拉夫列于1962年提出的振动评价标准，考虑了水电机组尺寸（以水轮机名义直径为代表）对机组振动的影响［3］。目前应用最广泛的两个振动评价国际标准，分别为ISO 7919-5∶2005和ISO 10816-5∶2000，由机组转速确立不同的振动范围，进而对振动水平进行评价［4-5］。目前各方采用的振动评价方法，主要还是建立在数据统计和分析的基础上，其本质也是实践经验的总结，因此有必要对近几年我国积累的水电机组振动数据进行统计分析，探究振动评价的新方法。

立式水轮发电机中安置推力轴承的机架统称负荷机架，它承受机组转动部分的全部重量、水轮机的轴向水推力、机架自重及作用在机架上的其他负荷，是机组的重要结构部件，其振动水平直接影响机组的运行稳定性。本文以混流式机组的负荷机架振动为例，从机架应力分析出发，建立负荷机架振动模型，对振动水平进行评价。

2 振动参数的确立

负荷机架是由中心体和多个支臂组成的钢板焊接结构。机架将所受动静载荷均匀的传递给各个支臂，支臂在弯曲应力作用下产生振动，因此通常在支臂上布置传感器测量机架振动。本文通过对支臂进行应力分析和挠度计算，研究表征动静载荷关系的振动参数。

2.1 受力分析与挠度计算负荷机架单个支臂内端的弯曲应力可按下式计算［6］：

式中：P为单个支臂上承受的负荷，P总为机架所受总负荷，P=P总/m，m为支臂数；L为支臂长度；J0为支臂内端横截面的惯性矩，其中 H0、b0、δ0、h01的定义如图1所示。

式（1）中的弯曲应力产生的挠度为［6］：

式中：E为支臂材料的弹性模量；K为计算系数，当支臂几何相似时，K为常数。对比式（1）和式（2）可得：

图1 负荷机架支臂横截面示意图

图2 简化的负荷机架支臂横截面图

式（3）表明，材料相同、几何相似的发电机负荷机架在相等的应力水平下，挠度的大小与机组的线性尺寸成比例。

现实中，随着水电机组容量的不断增大，机组的尺寸也越来越大，而机架的刚度不可能随尺寸的增加同比例增加，尤其是为了满足经济性的要求，现在机组设计多采用轻型化的结构，刚度不足的问题愈加突出。在相同的应力水平下，尺寸较大的机组部件抵抗变形的能力较差一些，直接影响机组振动的大小。

2.2 振动参数的提出为简化机架支臂的受力分析及计算，假定机架支臂截面为一矩形，宽为b，高为h，支臂长仍为L。简化后的机架支臂横截面如图2所示。

机组的尺寸以水轮机直径为代表，若存在D/L=Kl，代入以上两式，并消去h，得

若机组结构相似，即机架支臂及其他机组各部件几何相似、尺寸对应成比例，K、Kl、bD均为常数，因此Kv为常数。

由上得出的d实际上代表了机架在静荷载作用下的挠度，而在实际运行中，机架的振动是在动静荷载综合作用下的结果，设其振动值为V，引入无量纲量进而定义实际上反映了机架所受的动静荷载的比例关系，代表了机架在动静荷载综合作用下的振动特性，本文选用其作为振动建模的因变量参数。

2.3 一个假定以上因变量参数V*是在机架及发电机结构相似的前提下提出的，具体为机组采用几何相似的机架支臂，且不同部件尺寸也对应成比例；在此前提下，它反映了动静荷载对机架的共同影响。而机组所受动荷载主要来源于水轮机传递而来的水流作用力，水流作用力及其产生的转动力矩由顶盖和主轴传递给发电机，引起负荷机架的振动。进而，若水轮机过流部件内的水流运动相似，则水流对转轮的作用力对应成比例，转轮表面形成的动应力与静应力对应成比例。动静应力之比决定了机组由于振动而引起的输出功率损耗，因此对相似水轮机，相似水力条件引起的机组振动所导致的相对功率损耗也是一致的。

基于上述假定，对相似机组（水轮机相似，发电机结构相似），V*反映了机架所承受的动静荷载的比例关系，代表了由于机架振动引起的机组相对功率损耗；而单位转速n为机组转速）反映了相似水轮机的转动特性，故选用其作为振动建模的自变量参数。

3 建模与评价

本文收集、汇总了国内47个水电厂、共计101台混流式机组的振动数据，均是在原型机组上测得，且均为伞式机组，故负荷机架振动对应机组的下机架振动。以下运用最小二乘原理建立振动回归模型，划分振动区域，对振动水平进行评价。

3.1 最小二乘原理最小二乘法是一种数学优化方法，其最大的特点是，将随机变量的实测值与回归值（也称拟合值）差的平方和作为优化依据，使其达到最小的模型即为最合适的回归模型。

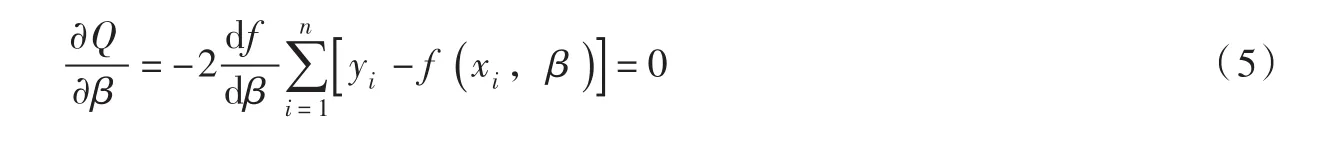
3.2 振动模型的建立记各机组下机架振动为V（相对功率在70%以上、相对水头在75%～120%范围内对应振动值），根据机组转速n、水轮机直径D、额定水头H，求得单位转速n11与振动参数V*，如表1所示。

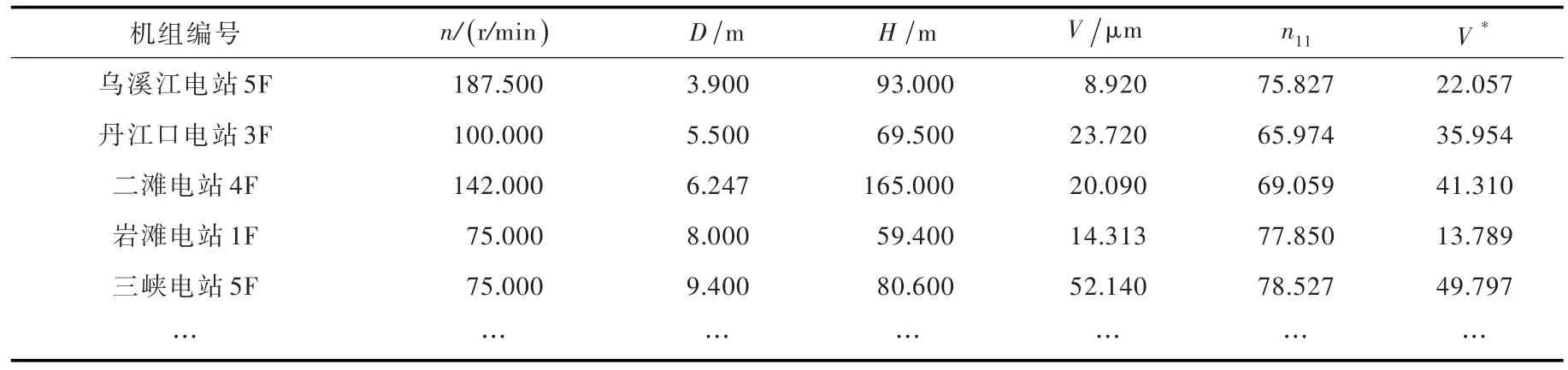
表1 各机组单位转速n11与振动参数V*对应表

根据表1中数据，选取Y=aXb指数模型，用最小二乘原理进行回归计算，使残差平方和Q最小的最优解为

3.3 振动区域的划分根据最小二乘原理建立的回归模型本质上是近似解，对某一实测点（x0，y0），其对应回归模型上点（x0，y1），记随机误差为 ε，ε=y0-y1。由于 ε～N（0，σ2）［8］，所以 P（y0-y1≤0）=0.5，实测值y0不大于回归值y1的概率为0.5，（-∞，y1）即实测值在50%置信水平下的置信区间。因此回归模型本身就反映了所有实测值在50%置信水平下的累积概率分布。

对水电机组而言，如果振动过大，将严重影响机组的运行稳定性，威胁机组的运行安全，因此应根据振动值的大小区分不同的振动水平。取不同大小的累积概率划分机组的振动范围，以该范围的上界值作为该振动水平对应的振动上限值。以此确定的振动区间，实测值落在该区间内的置信度在数值上大小等于所取的累积概率，即实测振动值不大于振动上限值的可信度。

本文取置信度水平为50%、92.5%和98%（此置信水平仅对统计机组的振动数据而言），分别作出下机架振动的累积概率分布曲线，将振动划分为A、B、C、D四个区域，建议以此作为评价振动水平的依据（见图3）。

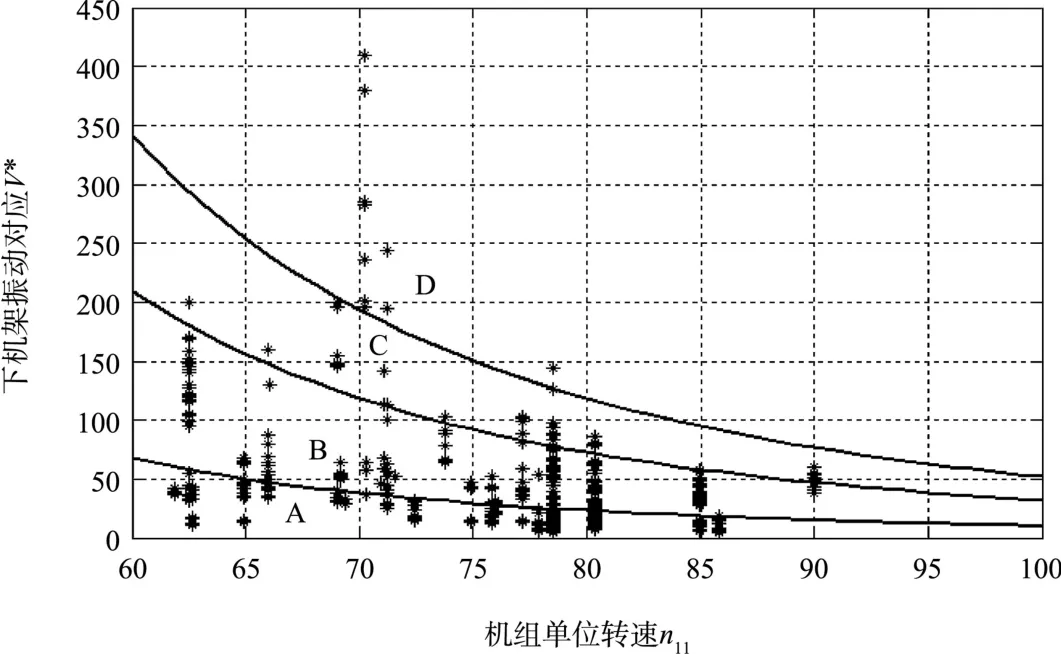
图3 下机架振动评价区域图（混流式机组-伞式）

A、B之间的界线——50%置信水平下的下机架振动值的累积概率分布曲线。

B、C之间的界线——92.5%置信水平下的下机架振动值的累积概率分布曲线。

C、D之间的界线——98%置信水平下的下机架振动值的累积概率分布曲线。

A区——适用于新投产的机组下机架振动的评价，在该区域运行的机组振动较小，机组运行安全稳定，状况良好。

B区——如果无导致其他相关不良迹象，如导轴承温度过高等，机组可以在该振动区域内长期运行。

C区——需对机组加强监视，并进行必要的额外检查。

D区——机组在此区域内运行极其不安全，须立即停机，并进行全面检查。

4 结语

随着水电厂自动化程度的不断提高，水电机组的振动监测技术已相当成熟且得到了广泛应用，同时也积累了大量的振动数据。因此利用现有数据进行统计分析，确立有效的振动评价方法，对开展水电机组后期故障诊断和状态检修有显著的指导意义。本文以混流式机组的负荷机架振动为例，对汇总的振动数据进行分析，取得了如下研究成果：（1）从负荷机架支臂的应力分析和挠度计算出发，提出了一个表征机架所受动静荷载关系的振动参数，该参数反映了机架在动静荷载综合作用下的振动特性；（2）根据“相似水力条件引起的机组振动所导致的相对功率损耗一致”这一假定，建立了振动参数与单位转速间的振动模型，该模型代表了相似机组（水轮机相似，发电机结构相似）的振动特性；（3）在不同的置信水平下，根据上述模型划分了A、B、C、D四个振动区域，以对机架振动水平进行评价，并提出了建议措施。

本文汇总的原始振动数据真实可靠，建立的回归模型残差和小，是评价水电机组振动的新思路。而任何评价准则的确定，既离不开理论分析的基础，也不能缺少现场测试的检验，两者缺一不可。文中相似机组振动特性相近的假定尚缺乏实测数据支持，需通过现场测试检验其可靠性。此外，振动回归模型的建立应基于尽可能广泛的振动数据，使其具备更强的可用性。

［1］ 刘晓亭，冯辅周.水电机组运行设备监测诊断技术及应用［M］.北京：中国水利水电出版社，2010.

［2］ 周叶，唐澍，潘罗平.HM9000ES水电机组故障诊断专家系统的设计与开发［J］.中国水利水电科学研究院学报，2014，12（1）：104-108.

［3］ 李启章.关于水轮发电机组振动标准的探讨［J］.水力发电学报，1992（1）：85-94.

［4］ ISO 7919-5：2005.Mechanical Vibration—Evaluation of machine vibration by measurements on rotating shafts-Part5：Machine sets in hydraulic power generating and pumping plants［S］.International Organization for Standardization.2005.

［5］ ISO 10816-5：2000.Mechanical vibration—Evaluation of machine vibration by measurements on non-rotating parts—Part5：Machine sets in hydraulic power generating and pumping plants［S］.International Organization for Standardization.2000.

［6］ 白延年.水轮发电机设计与计算［M］.北京：机械工业出版社，1982.

［7］ 邹乐强.最小二乘法原理及其简单应用［J］.科技信息，2010（23）：282-283.

［8］ 齐民友.概率论与数理统计［M］.北京：高等教育出版社，2004.

Evaluation of vibration on load frame of Francis unit

CAO Deng-feng，PAN Luo-ping，ZHOU Ye，XIA Wei
（China Institute of Water Resources and Hydropower Research，Beijing 100038，China）

The vibration state is one of the main indicators characterizing the operation stability of hydro⁃power unit.A non-dimensional parameter which reflects the relationship between dynamic and static loads is put forward，based on study on vibration performance on load frame of similar unit taking Francis units for example.Relative power consumption caused by the vibration which results from hydraulic factors is con⁃stant for similar units.Based on this assumption，a regression model between the vibration parameter and unit speed is finally established with the least square method.The range of vibration is divided into several different areas under different confidences to evaluate vibration state，and countermeasures are proposed.It turns out that it is an effective and feasible method for evaluating vibration state on load frame of Francis units.

Francis unit；vibration of load frame；vibration modeling；the least square method；evaluation of vibration state

TV737

A

10.13244/j.cnki.jiwhr.2014.03.019

1672-3031（2014）03-0327-05

（责任编辑：韩 昆）

2014-05-21

中国水利水电科学研究院科研专项（HM0145B212014）

曹登峰（1987-），男，河北平山人，硕士，助理工程师，主要从事水电机组状态监测与故障诊断研究。E-mail：caodf@iwhr.com