大跨度拱桥的稳定性分析

2014-04-09汪洋

建筑与预算 2014年3期

汪洋

(沈阳建筑大学土木工程学院，辽宁沈阳 110168)

0 引言

在我国桥梁系列形式中，拱桥是一种非常古老的桥型，因其跨越能力大、承载能力高、造价经济、养护维修费用少、造型美观等特有的优势，而成为建筑历史最悠久、不断发展的桥梁形式。大跨度拱桥更是在当代社会得到广泛的应用。

随着拱桥结构体系设计理念的日益独特和日渐新颖，施工技术的先进性，新材料的广泛应用性，拱桥日渐适应当代经济的快速发展，大跨度桥梁越来越受到设计师们的青睐。为此，对于桥梁尤其是大跨度桥梁的稳定性理论的研究就显得尤为重要。我国很多学者都对大跨度拱桥的稳定性做了很多的研究。谢幼藩和陈克济研究探讨了在均布对称荷载作用下钢筋混凝土拱桥面内承载力的非线性有限元分析［1-2］项海帆和钱莲萍［3］研究了单承重面拱桥侧向稳定问题，给出了稳定性实用计算方法。金伟良，顾淑兴等［4］进行了无横撑肋拱桥横向稳定性的研究，从理论上阐述了由于吊杆的非保向力作用使得拱肋的横向稳定性有所提高，并提出了计算无横撑肋拱桥侧倾屈曲的临界荷载的实用方法。桥梁结构稳定问题按性质划分有分支点失稳、极值点失稳和跨越失稳；按几何变形可划分为小挠度失稳和大挠度失稳；按材料特性可划分为弹性屈曲和弹塑性屈曲；按失稳的影响范围可分为整体失稳和局部失稳；按荷载类型划分可分为

静力失稳和动力失稳［5］。

本文将通过采用有限元分析软件Midas-Civil建立位于沈抚交接的动漫桥的有限元模型对其进行空间稳定性分析，对结构进行非线性分析。

1 工程简介

沈阳市浑河动漫桥是一座横跨浑河的大桥，本桥主桥采用6跨中承式飘带形提篮拱桥，桥位处水面宽约680米。主桥跨径为35+84+120+88+68+35=430m，其中最大跨度为3号拱120米。拱肋均采用矩形钢箱，在桥面设置系杆以连接主桥两端的端横梁，以此平衡主桥的水平推力。各跨拱肋均采用内倾17度布置，形成提篮拱的造型。

2 模型建立与分析

在拱桥稳定性的有限元分析中，分析类型依赖于其所采用何种稳定理论，大致可分为以下两类：若是基于经典的弹性理论，那么该种稳定分析属于第一类稳定分析，若是基于非线性的挠度理论，那么该种稳定分析属于第二类稳定分析。

当作用在拱结构上的外力荷载达到某一量值时，拱轴线就会在竖直平面内开始偏离对称变形状态向反对称的弯压平面挠曲转化，这种现象我们称之为拱的面内屈曲。当拱结构受到的的外力荷载达到某一量值时，拱结构也可能离开其平面平衡状态而向空间弯扭形式的平衡状态过渡，这种现象我们称之为拱的面外屈曲，也叫侧倾失稳。上述的这两种失稳现象统称为分支失稳问题，即第一类稳定问题。由于工程中各种拱结构都不是理想结构，都具有初始缺陷，结构的荷载-挠度曲线没有分岔点只有极值点，结构的弯曲变形性质没有变化，此类失稳就是极值点失稳，此类稳定问题即为第二类稳定问题。

沈阳浑河动漫桥双肋式梁拱组合体系拱桥，拱肋间没有横撑，其侧向刚度偏小，容易在横向荷载作用下出现较大的侧向变形而发生失稳破坏。这种形式的拱桥一般其面内稳定性比面外稳定性大，失稳破坏的形式一般为侧倾失稳，而侧倾失稳可能发生在弹性范围内或塑性范围内，但并不绝对，也可能会发生在弹塑性范围外。

本文将先进行第一类稳定系数的计算，因实际结构含有无法预估的初始缺陷，结构的荷载-挠度曲线没有分岔点只有极值点，结构的弯曲变形性质没有变化，其实际失稳形式必然是第二类失稳形式，但在设计和计算中都很难准确的模拟初始缺陷，因此大多数情况下计算得到的都是第一类稳定系数，通常第一类稳定系数是第二类稳定系数的上限，这样就具有一定的参考意义。同时如果侧倾发生在弹塑性范围内，这种特征值的计算方法得出的临界荷载是偏于不保守的，必须考虑几何与材料非线性的效应，如此才能得到比较正确的临界荷载。本文采用Midas-Civil建立全桥空间模型来计算第一类稳定屈曲特征值，全桥主要分为承台、拱座、拱肋、主梁、吊杆横梁及吊杆几部分。承台、拱座、混凝土部分拱肋采用实体单元建立；吊杆采用桁架单元建立；刚拱肋、主梁及吊杆横梁采用梁单元建立。钢筋混凝土的结合段采用刚性连接进行模拟，承台底部进行固结处理，采用位置荷载系数法对吊杆施加初拉力。

通过两种工况计算全桥稳定性，通过Midas-Civil屈曲分析功能可直接得出各模态下的特征值，取经计算得到的最小特征值作为全桥在该工况下的稳定系数。

全桥计算模型采用的工况有以下两种：

工况一：恒载

工况二：恒载+全桥活载

在两种工况下经由Midas分析所得的成桥状态下屈曲特征值如表1所示。

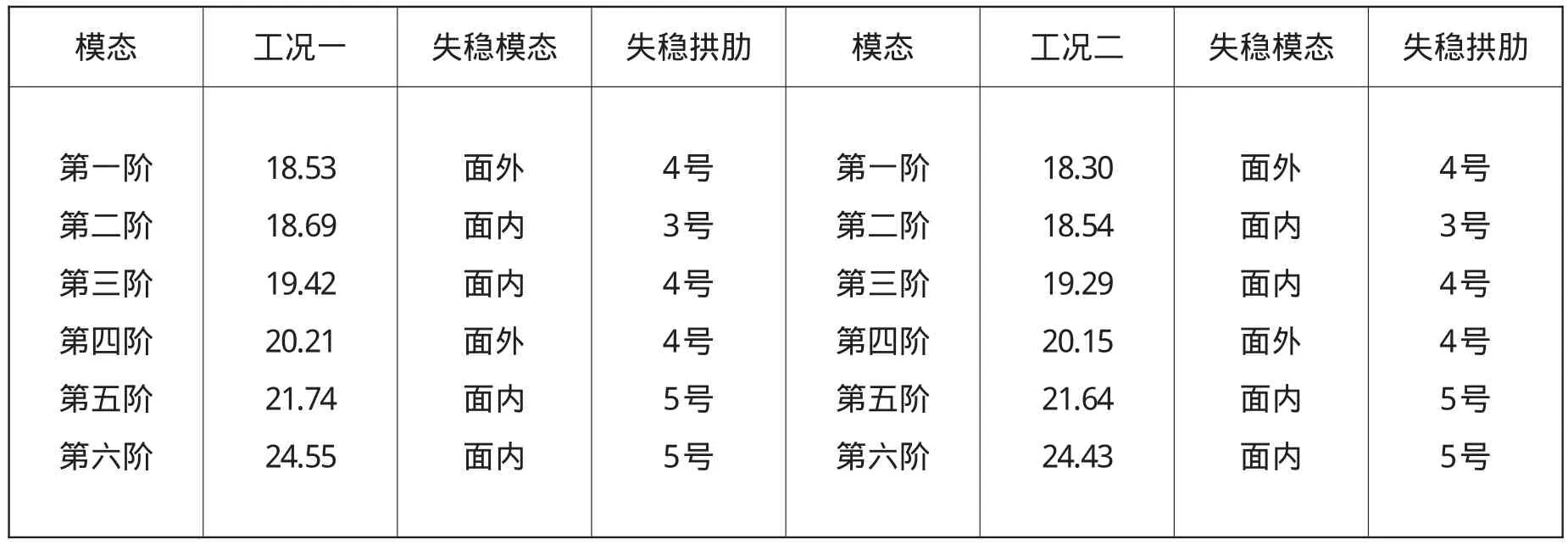
表1 成桥状态下屈曲特征值

从上表中我们可以看到在两种工况下全桥前六阶的屈曲特征值及相应的失稳模态，取两种工况下的最小特征值作为全桥的稳定系数，那就是工况二下的第一阶模态，其特征值为18.30。在工况二作用下，该桥的稳定系数最小，也是该桥处于最不利稳定状态。从上表中可以看到，虽然本桥为无横撑的内倾拱，但全桥的失稳模态无论是工况一还是工况二的情况下绝大部分都为面内失稳。从表1中可以直观看出全桥处于最不利稳定位置为4号拱，第一阶皆为面外失稳，且在成桥状态的两种工况下屈曲特征值最小。所以下文将对最不利位置的4号拱进行模拟分析。4号拱肋处的结构形式及参数为：4号拱肋的跨径为88 m，矢高34.7m，拱轴线方程为y=-0.02091415x2+34.7，拱顶钢箱截面高2.0m，拱脚控制截面高4.5m。

3.1 单拱肋第一类稳定分析

通过以上模拟分析，全桥稳定性能最不利位置位于4号拱拱肋，所以将单独对4号拱肋进行线弹性稳定性分析。计算分析结果见表2。

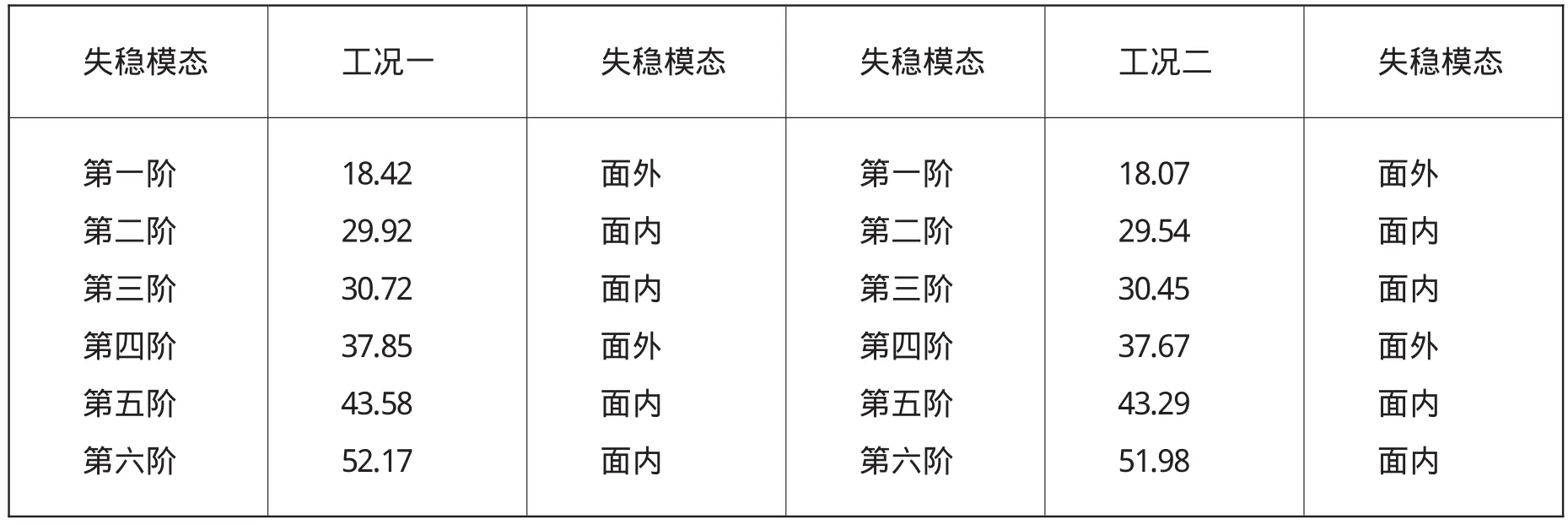
表2 成桥状态下屈曲特征值

表2是成桥状态两种工况下4号拱单拱肋的前六阶的屈曲特征值和对应的失稳模态，其中取最小的屈曲特征值作为该拱肋的稳定系数，在这两种不同工况下的稳定系数分别为18.42、18.07。其失稳模态皆为面外失稳。通过表2 可以清楚的看到在工况二作用下拱的稳定系数最小为18.07。此时拱处于最不利稳定状态。从失稳模态中可清楚的看到第一阶的失稳均为面外失稳，而且两种工况下前六阶失稳模态中以面外失稳特性最为显著，所以通过以上计算结果可以得出该桥的拱肋主要失稳形式为面外失稳，在稳定设计及其施工过程中由面外失稳控制。

3.2 几何非线性的稳定

上一节计算得到的屈曲特征值至考虑了材料的线弹性阶段，所得到的稳定系数是非线性稳定的上限，只具备一定的参考价值。以下将进行此拱桥单拱肋的几何非线性稳定分析。拱桥的几何非线性稳定分析主要是指在荷载的作用下，荷载压力线与拱轴线不重合的问题。在施工阶段中压力线随施工过程的不断变化、各种施工造成的偏差、施工预拱度的设置误差、拱轴线的弹性压缩等［13］，这些都会造成拱桥的结构刚度与其位移的关系成非线性。所以拱的失稳可以说是属于第二类失稳。

大跨度拱桥的几何非线性主要来自三个方面:

(l)轴力对弯曲刚度的影响；

(2)大位移产生的结构几何形状变化引起的几何非线性效应；

(3)稳定分析的平衡方程应在结构受载以后的变形位置建立。

因此，结构位移与荷载之间的将呈现非线性关系。本文采用Midas-civil建立模型计算了两种工况下，考虑几何非线性情况的单拱肋的稳定系数，选择考虑拱顶节点的Z方向位移逐渐增大时荷载系数的变化。分析过程中选择位移控制的方法，计算时输入一个较大的位移值，分成对应的步骤，每一次增加一定的位移增量，这样通过计算就可以得到拱肋失稳时的荷载系数。当位移增量达到一定的临界值时，荷载系数达到极限值，伺候荷载增量会自动减小。为准确得到结果，将收敛误差控制在1m m左右。当荷载系数增加到某个数值的时候，荷载增量即使很小，位移也很快增大，则认为此时的荷载就是使结构发生失稳破坏的临界荷载值，对应的荷载系数即为稳定系数。在Midas-Civil程序里，计算中可得到在每一步的位移增量下所达到的荷载系数。当位移忽然增大，而对应的荷载系数改变量很小时，认为结构已经达到了临界荷载值。

考虑几何非线性因素后，失稳模态仍为面外失稳。两个工况下各个子步骤对应的荷载系数值。见表3和表4。

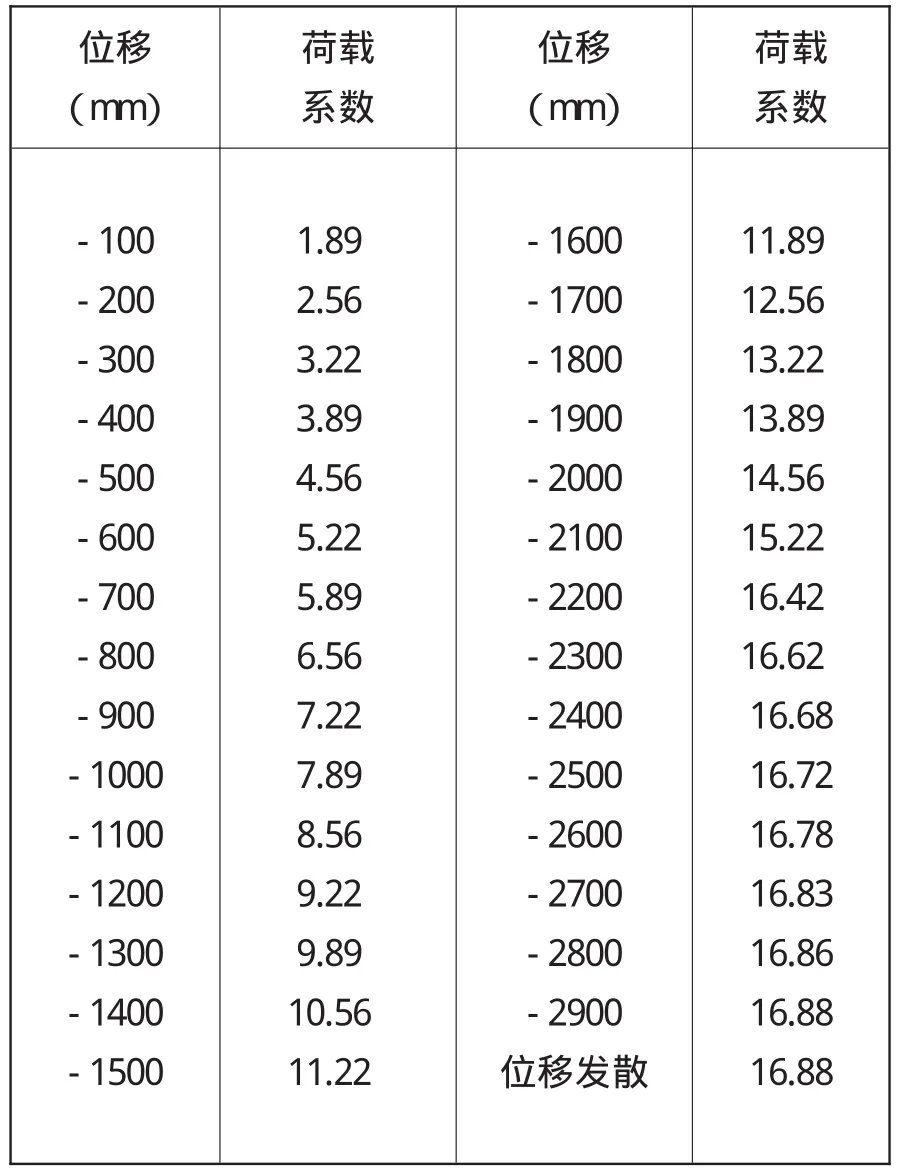
表3 工况一作用下位移—荷载表

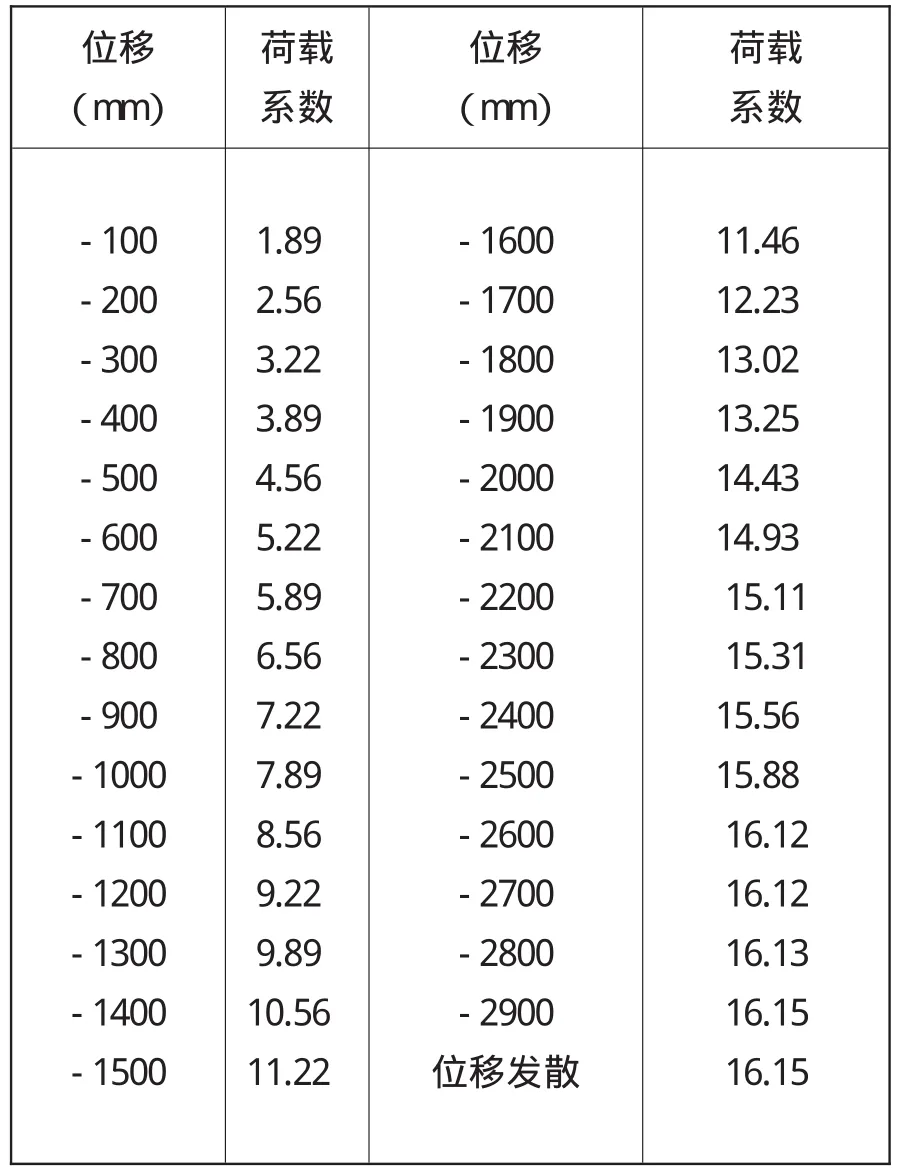
表4 工况二作用下位移—荷载表

从以上图表中可以看出，拱桥结构体系在两种工况下，荷载系数分别为16.88、16.15时，计算不再收敛，位移呈现发散状态，此时即为结构出于失稳的状态，此时的荷载系数就是结构的稳定系数。

通过以上两种分析计算，可以看出在考虑几何非线性和不考虑几何非线性时的稳定系数存在差异，两种工况下的稳定系数见表5。

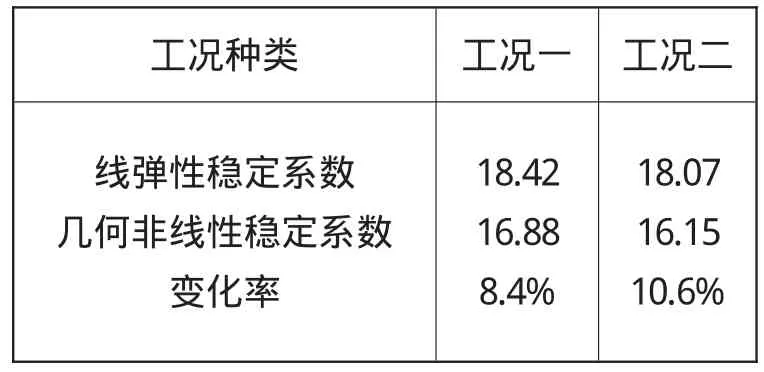
表5 两种工况下的稳定系数

从上表中数据可以看到，考虑几何非线性因素后，结构的稳定系数相较有所降低，而工况二的稳定系数仍为最小值，即为最不利工况。结构在工况一即恒载作用下弹性阶段的稳定系数较几何非线性阶段的稳定系数降低了8.4%，工况二作用下弹性阶段的稳定系数较几何非线性阶段的稳定系数降低了10.6%。以上结果说明了线弹性稳定分析所得到的稳定系数是考虑非线性因素的稳定系数的上限。由此可以看出几何非线性对稳定的影响是不可忽略的，如稳定分析中不考虑几何非线性因素，得到的稳定系数偏于不安全，在施工过程中存在安全隐患。所以在结构设计时，尤其是对于外形复杂、跨越长度大的拱桥结构，必须考虑几何非线性的因素影响。

3.3 双重非线性的稳定

结构在荷载作用下，当荷载达到一定值时，局部位置的应力可能会达到或超过材料的弹性极限，进入非线性阶段，进而产生塑性铰，致使结构发生失稳现象。所以采用特征值屈曲分析和只考虑几何非线性对结构进行稳定分析所得到的结果仍旧偏于不保守。因拱桥的主要承重结构是拱肋，拱肋为全桥稳定的关键所在，所以此处考虑拱肋的材料非线性，进行材料非线性稳定分析。

工况一作用下的荷载—位移曲线的拐点对应的荷载系数是10.53，而工况一的第一类稳定系数为18.43，不难看出在考虑了材料非线性后结构整体的稳定系数相对降低了很多，由此可以看出材料非线性对结构的稳定性存在非常重要的作用，材料非线性对结构稳定性的影响远大于几何非线性。不论在设计施工过程中，大跨度拱桥结构的稳定性分析必须考虑材料非线性，确保得到准确的稳定性系数。