基于空间扫描思想的复杂蒸发冷却式换热器通用模拟方法
2014-04-09杨明洪李先庭石文星王宝龙
李 筱 杨明洪 李先庭 石文星 王宝龙
(清华大学 建筑学院 建筑技术科学系 北京 100084)
蒸发冷却式换热器是一种融合了水冷式换热器和冷却塔于一体的紧凑式换热器,其换热系数为500~1000 W/(m2· ℃)[1-2]。与风冷式相比,蒸发冷却式换热器具有较高的换热效率和较小的传热温差,因此它所需要的换热面积比风冷式小得多,并且风机耗电约为风冷式的1/3[3];与水冷式相比,蒸发冷却式换热器换热效率并无明显降低,并且结构简单,占地面积小,所消耗的水泵功率也只是水冷式的1/8~1/4,实际循环水耗散量也小于水冷式系统。因此,发展和推广蒸发冷却式换热器,对于节能减排具有重要意义。
根据管内被冷却的流体有无相变,蒸发冷却式换热器可分为蒸发式冷凝器和蒸发式冷却器两大类。前者主要应用于制冷系统中,后者广泛应用于工业过程。研究表明:在环境温度35 ℃~49 ℃的范围内,采用蒸发式冷凝器的制冷系统所消耗的总功率比风冷式系统下降了11.7%~20.3%,系统的COP提高了31.7%~50.6%[4]。蒸发式冷却器也称为闭式冷却塔,根据塔内是否有填料, 还可分为无填料型和有填料两种类型。当带有填料时,空气和喷淋水在具有大比表面积的填料中进行二次热质交换,可以有效降低喷淋水温,使换热器的换热量比无填料时提高约7%~18.4%[5]。
在蒸发冷却式换热器中,有三种流体参与流动和换热:被冷却的高温流体在管内流动,空气在管与管的空隙间流动,喷淋水主要在管外表面以水膜的形式流动。三者的流动和换热高度耦合,传统换热器的模拟方法难以适用于蒸发冷却式换热器。目前,对蒸发冷却式换热器的模拟研究主要集中在理论分析、CFD流场模拟和换热性能数值模拟三方面。
在理论分析模型方面,一般是假设空气和冷却水纯逆流,即在一维流动的前提下,从传热传质的微分方程出发,得到换热性能的解析表达式[6-8]。由于理论分析模型中所假设的物理模型与实际蒸发冷却式换热器有较大差别,所以其计算精度有限,主要用于指导蒸发冷却式换热器的设计方向。
由于蒸发冷却式换热器中存在管内、外两侧,有三种流体参与,在喷淋水和空气的界面上除了热量传递还有质量传递,整个过程是复杂的多相流动,导致整个换热器的建模和求解过程非常复杂。因此目前CFD技术多用于假定换热管表面特征(已知热流或温度分布)下的流场(气体场和液体场)计算[9-10]。CFD模拟结果主要用于为后期传热计算提供输入参数[11]。
在换热性能模拟方面,Zheng等[12]对采用椭圆管的闭式逆流塔建立了二维分布参数模型,并与实验结果对比,表明冷却水出口温度与实验结果吻合地比较好;董俐言等[13]从能量守恒和质量守恒方程出发,建立了板式蒸发式冷凝器的二维分布参数模型,能够较好地预测板式蒸发式冷凝器的性能。然而上述模型只能用于求解特定的流动和结构形式的蒸发式冷凝器。当流动或结构形式改变时,模型和求解方法需要修改甚至需要重写。主要原因是上述模型无法用一种统一的方法同时描述光管区域和填料区域,也无法统一处理有喷淋和无喷淋的情况。
本文参考CFD计算中的网格划分思想,按照空间位置对蒸发冷却式换热器进行三维网格划分;建立一种统一处理不同性质(含传热管节点和填料节点)、不同模态(喷淋态和无喷淋态)节点的传热传质模型;最后采用空间扫描方式依次对各个节点进行求解。该模型的求解算法与各流体的流动形式无关,即三种流体可以是任意的三维流动;模型中的节点可以是传热管段,也可以是填料或其他结构形式;管内被冷却的流体既可以是热水,也可以是两相的制冷剂。因而,本模型具有广泛的适应性,是一种通用的蒸发冷却式换热器的数值计算模型。
1 模型建立
1.1 模型简介
为便于模型的简化,需做出如下假设:
1) 流动和传热传质达到稳态;
2) 相邻节点之间,各种流体除了在其流动方向之外,没有质量的传递;
3) 相邻节点之间,不考虑管壁的轴向导热、空气之间的热对流和管壁之间的热辐射;
4) 忽略水膜与空气表面的热阻影响,认为水膜表面饱和湿空气的温度与水膜温度相等;
5) 传热管外表面完全被水膜润湿;
6) 忽略换热器与环境之间的换热,忽略弯头部分的散热。
下面以图1所示的带填料的蒸发冷却式换热器为对象,建立其三维分布参数模型。
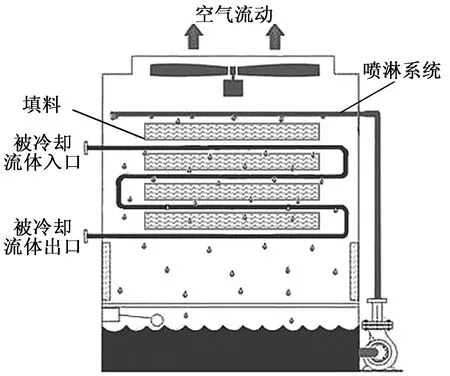
图1 带填料的蒸发冷却式换热器示意图
该模型的输入参数包括以下三类:
1)换热器的结构参数。盘管区域的结构参数包括管内直径di、管外直径do、管长L、管程数N、管排数M以及管之间的纵向间距s1和横向间距s2,填料区域的结构参数包括填料的高度Hf。
2)流体的流动形式。描述三种流体的流通路径和流动方向,即描述节点之间的流动联系。
3)流体的入口参数。空气侧包括入口空气温度ta,in、含湿量da,in、相对湿度φa,in和迎面风速分布矩阵Ua,管内被冷却流体侧包括流体种类、入口温度tr,in、压力pr,in、焓hr,in和总流量Mr,in,喷淋水侧包括喷淋水量的分布矩阵Mp。
对于设计和运行良好的闭式冷却塔,可近似认为迎面风速和喷淋水量的分布是均匀的。若要研究它们的不均匀性对换热器性能的影响,则可通过实验测量、CFD模拟或理论计算等方法得到相关参数的分布矩阵,然后导入本模型,进而计算它们的换热性能。
1.2 几何模型构建
本模型是三维分布参数模型,其几何模型的建立包括以下两个步骤。
1)节点划分。将换热器中划分为总数为inum×jnum×knum的三维空间节点,如图2所示。其中inum为管长方向划分节点总数;jnum为管程方向划分节点总数;knum为管排方向划分节点总数。本模型中有传热管段和填料两类节点,它们是以传热管段或填料为中心的微元体。
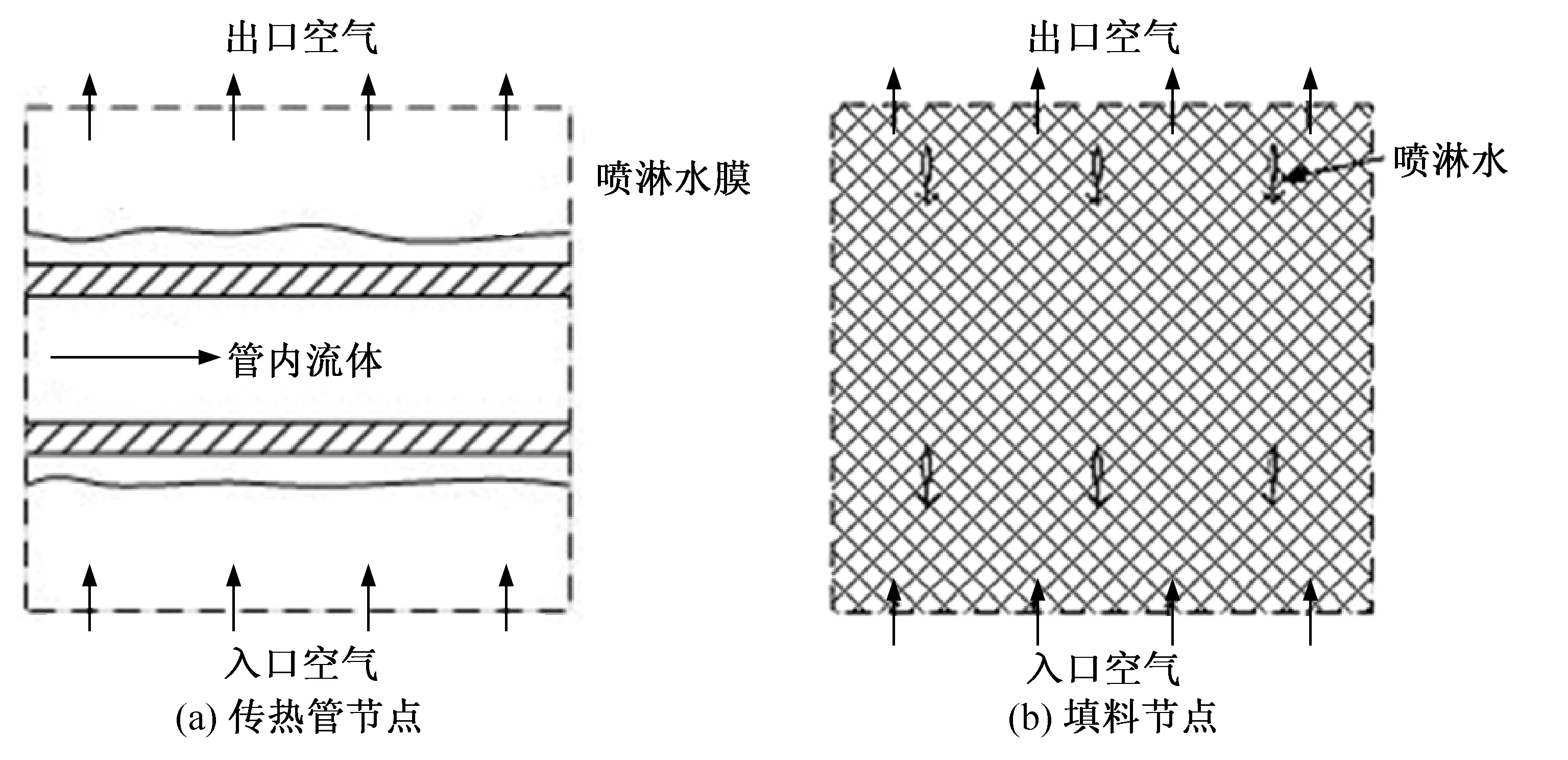
图3 节点内部流动示意图
2)流动描述。用数学语言定量描述各节点之间流体的流动方向。本模型中采用三维向量(ri,rj,rk)、(ai,aj,ak)、(pi,pj,pk)分别指节点(i,j,k)中管内流体、空气、喷淋水的上游方向,即节点(i,j,k)中三种流体对应的上游分别是节点(i+ri,j+rj,k+rk)、(i+ai,j+aj,k+ak)、(i+pi,j+pj,k+pk)。对于填料节点,节点中不含管内流体,对应用向量(0,0,0)表示填料节点。若某节点中某一流体的上游(i*,j*,k*)不属于全部节点的集合{(i,j,k)|1≤i≤inum,1≤j≤jnum,1≤k≤knum},则表明该节点中该流体的上游参数为换热器的入口参数。
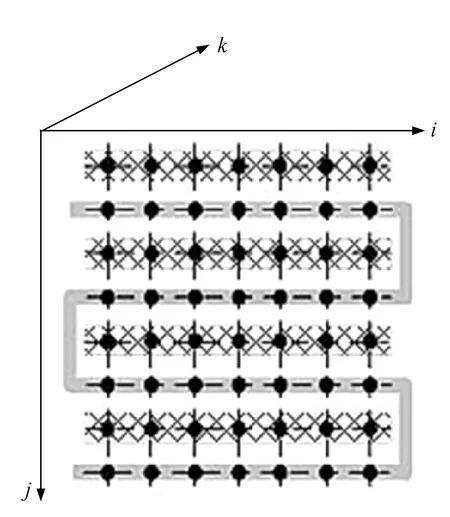
图2 空间节点划分示意图
1.3 节点内传热传质过程建模
在节点内部,各流体之间发生热量传递和质量传递过程。本文仅对传热管节点和填料节点进行建模,其节点内部流体的流动如图3所示。本建模方法不局限于这两类节点,甚至可以是开式冷却塔、风冷换热器以及管翅式换热器等其他结构类型的节点。
在本模型中,对于节点内部,认为管内流体侧和喷淋水侧的状态参数的分布是均匀的,而对于空气侧,则认为空气的状态参数的分布是不均匀的,其平均参数取为进、出口参数的平均值。
1.3.1传热管节点建模
在传热管节点中有三种流体参与流动和传热。管内流体和管表面的喷淋水膜均与管壁发生对流换热;喷淋水膜和空气之间既有对流传热过程,也有对流传质过程。
管内流体和喷淋水膜之间的传热量为:
(1)
式中:Ao为节点管外表面积,m2;Ai为节点管内表面积,m2;R0为污垢热阻和管壁导热热阻之和,取2.0×10-4m2· ℃/W;tr为管内流体温度, ℃;tp为喷淋水膜温度, ℃;αr为管内流体与管壁内表面之间的对流换热系数,W/(m2· ℃);αp为喷淋水膜与管壁外表面间的对流换热系数,W/(m2· ℃)。
管内流体和内管壁之间的对流换热系数可通过式(2)得到[14]:
(2)
式中:x为管内流体的干度;λ为管内流体的导热系数,W/(m2· ℃);Re=104~1.2×105;Pr=0.7~120;αl为单相区的换热系数,W/(m2· ℃)。
水膜和圆管表面的对流换热系数采用Parker 和Treybal[15]总结的公式:
(3)
式中:tp为水膜温度, ℃;Γ为单位管长的喷淋密度,kg/(m·s)。
喷淋水膜和空气之间的传质量为:
Ma,p=αdAo(dap-dam)
(4)
式中:dap为该节点中的水膜温度下饱和空气的含湿量,kg/kg干空气;dam为节点进出口空气的平均含湿量,kg/kg干空气;αd为喷淋水膜和空气之间的对流传质系数,kg/(m2·s)。
喷淋水和空气之间的对流传质系数尚没有成熟的通用公式,一般可以通过实验结果拟合成如下形式:
(5)
式中:m、n为拟合系数;Ga为最小截面处空气的质量流量,kg/(m2·s)。
喷淋水和空气之间的潜热传热量为:
Qa,latent=rMa,p
(6)
式中:r为水在水膜温度下的潜热,J/kg。
喷淋水和空气之间的显热传热量为:
Qa,sensible=αaAo(tp-tam)
(7)
式中:tam为节点内空气的平均温度, ℃;αa为空气和喷淋水之间的对流传热系数,W/(m2· ℃)。
根据刘伊斯关系式,空气和喷淋水膜之间的对流传质系数和对流传热系数满足:
(8)
式中:cp为空气定压比热容,J/(kg· ℃);Le为刘伊斯数,对水-空气系统,可近似认为Le-2/3≈1。
本节点中,管内流体、空气和喷淋水的得热量Qr、Qa、Qp分别为:
Qr=-Qr,p
踩下油门,伴随着强烈的推背感,V12自然吸气发动机传来高亢的嘶吼。变速箱如闪电般迅速升至下一挡,开启了新一轮的加速,伴随着阵阵烈焰,这辆性能怪兽如加农炮般被推向了前方。
(9)
Qa=Qa,latent+Qa,sensible
(10)
Qp=-Qr-Qa
(11)
1.3.2填料节点建模
填料节点中,只有喷淋水和空气参与流动换热。
喷淋水和空气之间的传质量为:
Ma,p=αVV(dap-dam)
(12)
式中:V为节点中填料的体积, m3;αV为填料的体积传质系数,kg/(m3·s)。
本节点中,空气得到的热量为:
(13)
式中:hp为节点中喷淋水的焓值,J/kg;ham为节点中空气的平均焓值,J/kg。
喷淋水得到的热量为:
Qp=-Qa
(14)
1.4 迭代原理及其算法
模型计算开始时,首先预设一个喷淋水入口温度,并对所有节点的参数赋予初值,然后通过扫描迭代的方法,依次计算每个节点中的传热量和传质量,并对节点中的流体参数进行更新。对于每一次迭代,从节点(1,1,1)开始,沿着坐标轴依次扫描,至节点(inum,jnum,knum)结束。当所有节点的参数均达到稳定时,则认为该喷淋水温下的迭代过程达到收敛,否则进入下一次迭代。由于喷淋水的流动为一个闭式循环,某个喷淋水温下迭代达到收敛后,还需判断喷淋水的进出口温度是否相等。若不等,调整喷淋水温,重新迭代;若相等,则认为该水温为实际喷淋水温,计算结束。
在第n次迭代过程中,扫描至节点(i,j,k)时,该节点的各流体参数用x(n)(i,j,k)形式表示。根据式(4)、(9)~(11)或式(12)~(14)可计算得到本节点中各流体的得热量Qr(n)(i,j,k)、Qa(n)(i,j,k)、Qp(n)(i,j,k),以及空气和喷淋水之间的传质量Ma,p(n)(i,j,k)。
迭代过程中,参数更新的原理是:当节点之间流动和节点内的传热传质达到稳定时,节点内各流体的得热量应等于相应流体的本节点与上游节点的焓差,空气和喷淋水之间的传质量应等于本节点空气和上游节点空气之间的含湿量之差。即利用能量守恒和质量守恒关系对节点中流体的参数进行更新。参数更新的原理可用关系式表示为:
Qa(n)(i,j,k)=ma(i,j,k)[ha(n+1)(i,j,k)-ha(n)(i+ai(i,j,k),j+aj(i,j,k),k+
ak(i,j,k))]
(15)
Qr(n)(i,j,k)=mr(i,j,k)[hr(n+1)(i,j,k)-hr(n)(i+ri(i,j,k),j+rj(i,j,k),k+
rk(i,j,k))]
(16)
Qp(n)(i,j,k)=mp(i,j,k)[hp(n+1)(i,j,k)-hp(n)(i+ri(i,j,k),j+rj(i,j,k),k+
rk(i,j,k))]
(17)
Ma,p(n)(i,j,k)=ma(i,j,k)[da(n+1)(i,j,k)-da(n)(i+ai(i,j,k),j+aj(i,j,k),k+
ak(i,j,k))]
(18)
利用式(15)~(18)可以分别更新得到第n+1次迭代过程中的三种流体的焓以及空气的含湿量,然后可以通过物性方程更新换热流体的其他状态参数。该次迭代过程中,任一参数的原来值为x(n)(i,j,k),更新得到更新值x(n+1)(i,j,k),定义该参数更新值与原值的变化率为:
(19)
第n次迭代完成后,全部节点内三种流体的各参数的最大变化率记为εmax(n),若εmax(n)小于预设的最大误差率ε0,则认为迭代已经收敛,计算喷淋水出口温度,然后判断喷淋水进出口是否相等,以决定是否需要调整喷淋水入口温度并重新迭代;否则,进入第n+1次迭代,直至收敛。
在迭代的过程中,为了加快收敛速度和提高收敛的稳定性,采用了如下四种办法:
1)在迭代过程中,对某一节点计算完后,立即更新本节点参数;
2)更新节点参数时,采用亚松弛因子调整更新值,即x(n+1)=(1-β)x(n)+βx*,0≤β≤1,其中x*为原本应更新的值,不同流体可以采用不同的亚松弛因子;
3)采用正反扫描的方法进行迭代更新,即对节点从(1,1,1)到(inum,jnum,knum)进行一次扫描迭代后,立即沿反向路径进行一次扫描迭代;
4)喷淋水温的迭代采用Steffensen迭代法或割线法,减少喷淋水温的迭代次数。
本文模型的求解过程如图4所示。
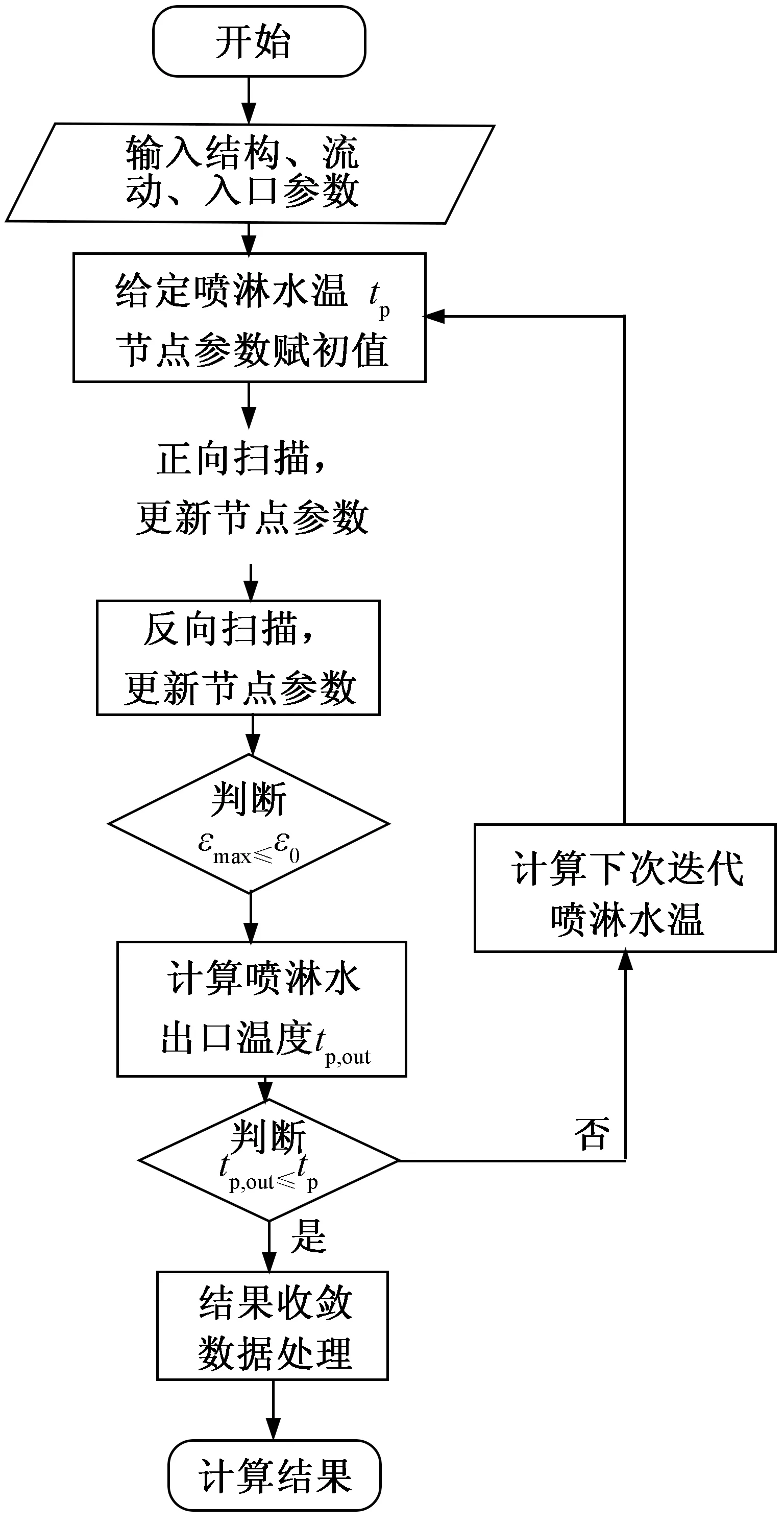
图4 模型求解算法流程图
2 模型验证
2.1 无填料型闭式冷却塔
本节采用文献[8]中的实验数据对无填料型闭式冷却塔的模型进行验证。该实验台的闭式冷却塔参数如下:管程数12,管排数19,管排之间为叉排,管外径10 mm,横向管间距0.06 m,纵向管间距0.02 m,管长1.2 m,总换热面积为8.6 m2。
模型中喷淋水膜和空气之间的传质系数采用文献[8]的实验拟合公式:
(20)
表1为文献中的实验的9组工况及其实验结果和采用本模型计算的模拟结果,实验涵盖了不同风量、不同冷却水流量以及不同入口空气相对湿度的工况,具有较广泛的代表性。可以看出,模拟冷却水出口温度的绝对误差大都在0.2 ℃以内;模拟的喷淋水入口温度与实验结果也非常接近,误差大都在0.35 ℃以内。可以认为模拟结果的误差在允许范围内,且具有较高的预测精度。
2.2 填料加盘管型闭式冷却塔
本节采用文献[16]中实验数据对填料加盘管型闭式冷却塔的模型进行验证。该实验台的闭式冷却塔参数如下:管程数8,管排数69,管外径12.7 mm,横向管间距0.029 m,纵向管间距0.036 m,正三角形排列,管长2.1 m,总换热面积为46.25m2。淋水填料为斜波填料,填料以整体的形式放置于盘管上方。
实验台盘管段水膜和空气的传质系数采用[16-17]:
(21)
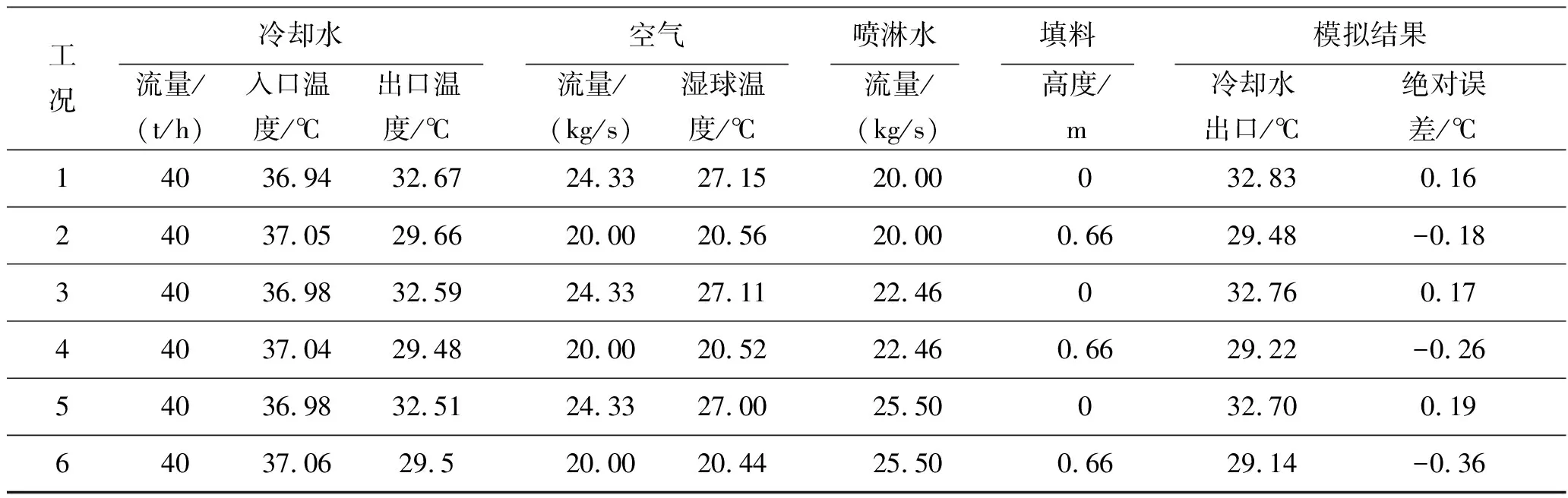
式中:AV为单位体积换热面积,m2/ m3;Rea为空气雷诺数,适用范围1.2×103 该淋水填料的体积传质系数为[16]: (22) 式中:Ga为空气质量流量,kg/(m2·s);Gp为喷淋水质量流量,kg/(m2·s)。 表1 无填料型闭式冷却塔实验工况及模拟结果 表2为文献中的实验结果和本模型的计算结果。实验工况中,分别有三组带有填料和三组不带填料的工况。从模拟结果来看,六组工况下模拟结果的相对误差均在5%以内,具有较高的精度。而且可以看出,不带填料的工况下冷却水出口温度的模拟结果偏高3.75%~4.25%,而带有填料的工况下冷却水出口温度的模拟结果偏低2.44%~4.76%,从而可以推测出,该实验工况下,式(21)计算得到盘管区域的传质系数偏低,而式(22)计算得到的填料区域传质系数偏高。 表2 有填料闭式冷却塔实验工况及模拟结果 本文针对现有蒸发冷却式换热器数值分析模型中存在的问题,提出了基于空间节点扫描思想的通用模拟方法,建立了可用于复杂结构、复杂流动、多模态蒸发冷却式换热器的仿真模型。 该方法参考CFD计算中的网格划分思想,按照空间位置对蒸发冷却式换热器进行三维网格划分;建立可统一处理不同性质(含传热管节点和填料节点)、不同模态(喷淋态和无喷淋态)节点的传热传质模型;然后采用空间扫描方式依次对各个节点求解。文章利用已有文献中的实验数据分别对无填料型和带填料型的两种闭式冷却塔的模型进行了验证,结果表明:模型对于两种闭式冷却塔都有良好的精度,该模拟方法具有良好的通用性,特别是对于复杂结构形式和复杂流动形式的换热器,本模型具有独特的优势。 [1] 朱冬生, 涂爱民, 蒋翔, 等. 蒸发式冷凝冷却设备的研究状况及其应用前景分析[J]. 化工进展, 2007, 26(10): 1404-1410.(Zhu Dongsheng,Tu Aimin,Jiang Xiang,et al. Research progress and application prospect analysis of evaporative condensing/cooling equipment[J].Chemical Industry Engineering Process, 2007, 26(10): 1404-1410.) [2] 彦启森, 石文星, 田长青. 空气调节用制冷技术 [M]. 第四版.北京:中国建筑工业出版社, 2006. [3] 韩广钧, 刘统建, 张玉梅, 等. 基于蒸发式冷凝器的空调冷水机组应用分析[C]//战略性新兴产业与科技支撑——2012年山东省科协学术年会论文集, 2012. [4] Hajidavalloo E, Eghtedari H. Performance improvement of air-cooled refrigeration system by using evaporatively cooled air condenser[J]. International Journal of Refrigeration, 2010, 33(5): 982-988. [5] 谢卫. 带填料的闭式冷却塔传热性能实验研究[D]. 上海: 东华大学,2013. [6] Zalewski W, Gryglaszewski P A. Mathematical model of heat and mass transfer processes in evaporative fluid coolers[J]. Chemical Engineering and Processing: Process Intensification, 1997, 36(4): 271-280. [7] 唐伟杰,张旭. 蒸发式冷凝器的换热模型与解析解[J]. 同济大学学报(自然科学版),2005,33(7): 942-946. (Tang Weijie, Zhang Xu. Heat Exchange Model and Its Analytic Solution of Evaporative Condenser[J].Journal of Tongji University(natural science),2005,33(7): 942-946.) [8] Hasan A A. Performance analysis of heat transfer processes from wet and dry surfaces: cooling towers and heat exchangers[M]. Helsinki University of Technology, 2005. [9] Gan G, Riffat S B. Numerical simulation of closed wet cooling towers for chilled ceiling systems[J]. Applied Thermal Engineering, 1999, 19(12): 1279-1296. [10] Gan G, Riffat S B, Shao L, et al. Application of CFD to closed-wet cooling towers[J]. Applied Thermal Engineering, 2001, 21(1): 79-92. [11] Hasan A, Gan G. Simplification of analytical models and incorporation with CFD for the performance predication of closed‐wet cooling towers[J]. International journal of energy research, 2002, 26(13): 1161-1174. [12] Zheng W Y, Zhu D S, Song J, et al. Experimental and computational analysis of thermal performance of the oval tube closed wet cooling tower[J]. Applied Thermal Engineering, 2012, 35: 233-239. [13] 董俐言, 王宝龙, 石文星, 等. 板式蒸发式冷凝器传热传质的数值模拟[J]. 制冷学报, 2013,34 (1): 10-17. (Dong Liyan, Wang Baolong, Shi Wenxing, et al. Numerical simulation on hear and mass transfer of plate evaporative condenser[J]. Journal of Refrigeration, 2013,34 (1): 10-17.) [14] 丁囯良, 张春路. 制冷空调装置仿真与优化[M]. 北京:科学出版社, 2001. [15] Parker R O, Treybal R E. The heat and mass transfer characteristics of evaporative coolers [J]. Chemical Engineering Progress Symposium, 1961, 57(32): 138-149. [16] 任勤. 基于冷却效率最优化闭式冷却塔性能研究及选型软件开发[D]. 上海: 东华大学, 2010. [17] 尾花英朗. 换热器设计手册(下册)[M].徐中权, 译. 北京: 石油工业出版社, 1982.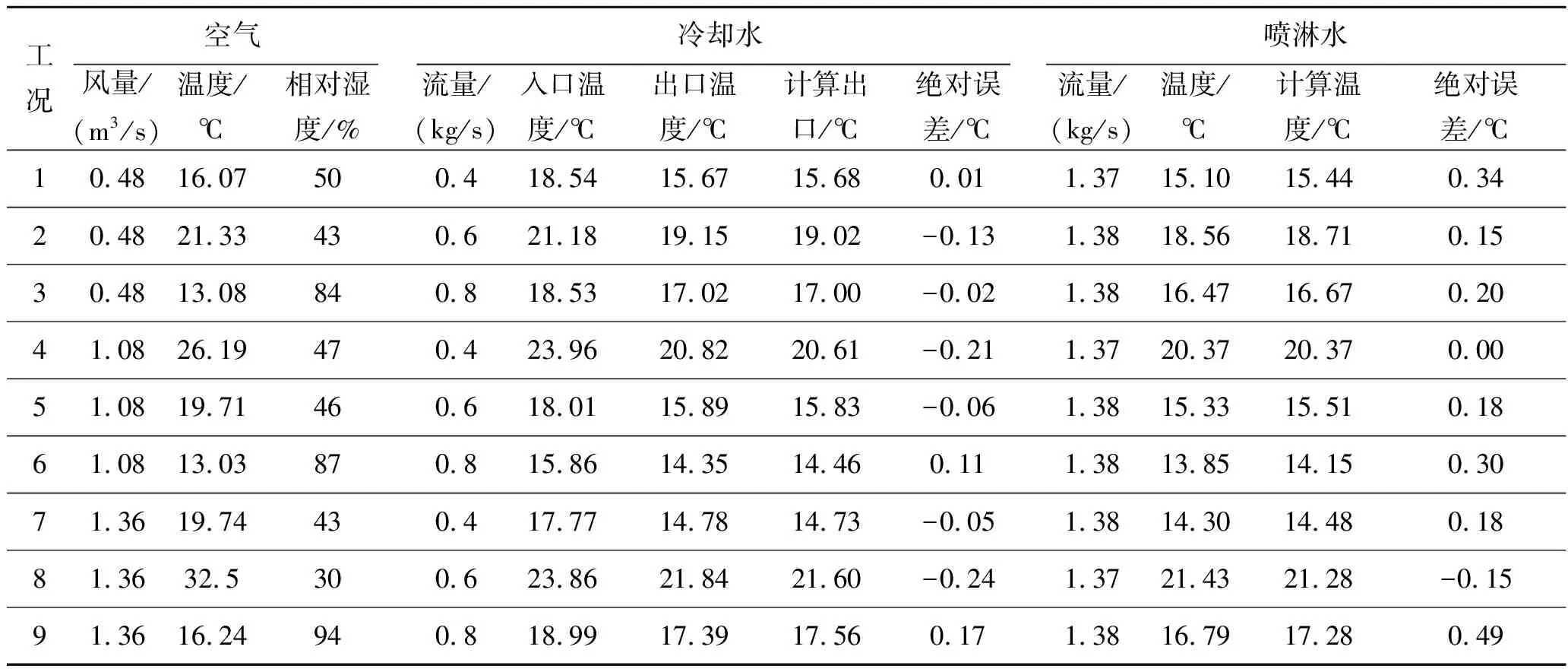
3 总结与展望
