用于道路均匀照明的LED自由曲面透镜设计

贺志华，董前民，王少雷，李 敏

(中国计量学院光学与电子科技学院，浙江 杭州 310018)

引言

随着LED技术的发展，LED长寿命、环保和节能等优点使得它的应用领域越来越广，在道路照明上正逐步代替传统高压钠灯，具有巨大的发展潜力[1-2]。基于LED的发光特性，如将其发出的光直接照在地面上，将形成照度极不均匀的大圆斑，不仅光能利用率低，还对远处的行人和车辆易造成眩光，增加交通事故的发生率，因此在照明系统中进行必要的二次光学设计才能充分合理地利用LED发出的光。由于二次光学设计关注的是能量的分配问题，因此非成像光学是设计的理论基础[3-5]。

从原理来看，自由曲面设计方法归结为试错法[6]和剪裁法[7]。试错法多凭设计人员经验，耗时过长；剪裁法于2002年由H.Ries和J.Muschaweck[8]提出，但该方法仍有多限制，不仅不能形成所需高配光效果的面型，且计算时间很长。根据我国《城市道路照明设计标准》的要求[9]，为将光尽量均匀投射到路面上，道路所需的理想配光是蝙蝠翼的矩形配光。目前常见的“花生米”路灯透镜常基于网格法[3,10]建模，该法虽较直观，但所得透镜要使配光的均匀度保持0.8以上，前提条件必须是LED发光面尺寸相对透镜本身尺寸小5倍以上，即点光源，若尺寸大了，其均匀度和有效照明区域均明显变小，而现在大功率LED多芯片集成封装多采用板上芯片封装形式(COB)，其尺寸已不能忽视。本文将采用精度更高的偏微分方程法，为解决该方法的可解性问题，这里引入合适的差分格式数值求解自由曲面面型的偏微分方程，其配光范围和尺寸大小可根据需要自由设定，且所得透镜在对大尺寸面光源配光时仍能保持较好的配光效果，应用上采用模块化阵列[11]，合理排列灯具，增加了其真实性。

1 自由曲面的构建原理与求解

本文采用偏微分方程法求解自由曲面透镜，其思路如下：首先推导光线与自由曲面间的相互关系，建立面型的偏微分方程，其次建立光源空间与被照面间的能量映射关系，进而化为一阶拟线性偏微分方程，最后采用有限差分法数值求解透镜面型，所得面型数据导入SolidWorks建立实体模型。

1.1 光线与自由曲面的偏微分方程推导

如图1所示，T为所求透镜表面上的任一点，φ为入射光线OT与z轴夹角，θ为OT在x-y平面上投影与x轴的夹角，因此入射光线的矢径为：

OT=ρ(φ,θ)I=ρ(φ,θ)(sinφcosθ,sinφsinθ,cosφ)

(1)

式中ρ(φ,θ),I分别为矢径OT的大小和方向。

图1 折射原理图Fig.1 Refraction schematics

由微分几何原理，自由曲面在T点的法向的单位矢量应是OT分别在θ和φ方向上的切矢量的叉乘，即：

(2)

式中，ρθ,ρφ分别为矢径大小在θ和φ方向上偏微分；Iθ,Iφ分别为矢径方向在θ和φ方向上偏微分。

令出射光线的单位矢量为O=TM/|TM|,nI，nO为入射和出射环境介质的折射率，再结合Snell定律的矢量式：

(3)

得到各分量间的关系式如下：

(4)

由式(1)、式(2)、式(4)化简得:

(5)

1.2 能量映射关系的推导

为使光源发出的光投射到路面形成矩形光斑，需建立光源空间和照明面间的映射关系。设光源发出的总光通量为Ф，预形成的均匀矩形照明面的长(道路方向)为L，宽(垂直道路方向)为W。由能量守恒，理论上在照明面上的平均照度Ev=Ф/LW。如图2所示，对光源辐射角和照明面的网格划分建立相应的映射关系，即图中的黑影的一一对应关系。因此要形成矩形光斑，经相同φ角和矢径大小下的环带射出的光线应恰好落在一矩形的边上。设该矩形在第一象限的顶点坐标为(X，Y)，且X/Y=W/L，则由能量守恒关系式

(6)

得到：

(7)

式中φm为光源最大半发光角。

图2 LED光源与照明面能量映射关系Fig.2 Energy mapping between LED source and lighting surface

在第一象限内，对路面上的点M有，当θ∈[0,π/4]时，光应投射到矩形的长上，即x=X，y/Y=θ/(π/4)；当θ∈[π/4,π/2]时，光应投射到矩形的宽上，即y=Y，x/X=[(π/2)-θ]/(π/4)。综合得在第一象限内LED发出的光线在投射到路面上点M的坐标为：

(8)

令f[φ,θ,ρ(φ,θ)]=ρφ+ρθ，则化成一阶拟线性双曲型偏微分方程：

(9)

将φ和θ分别划分成J份和K份，组成(φj，θk)网格线，运用Runge-Kutta法和Lax-Wendroff[12]差分格式(其截断误差只有ο[Δθ2+Δφ2)]即可求得其余矢径大小，再通过球坐标和直角坐标的转换便得到所求面型的数据。

2 仿真结果与分析

2.1 结果仿真

我国城市路灯的安装为尽量避免眩光，一般采用12m左右的高杆灯。这里预在10m高下形成道路方向120°配光，垂直道路方向75°配光的均匀照明区域。根据以上原理，透镜材料选用PMMA，经matlab编程求出1/4路灯透镜的面型(如图3(a)所示)，计算时间低于1s。再通过SolidWorks三维建模软件构建透镜的实体模型(如图3(b)所示)，其长×宽×高的尺寸为28.1mm×14.8mm×10.6mm。

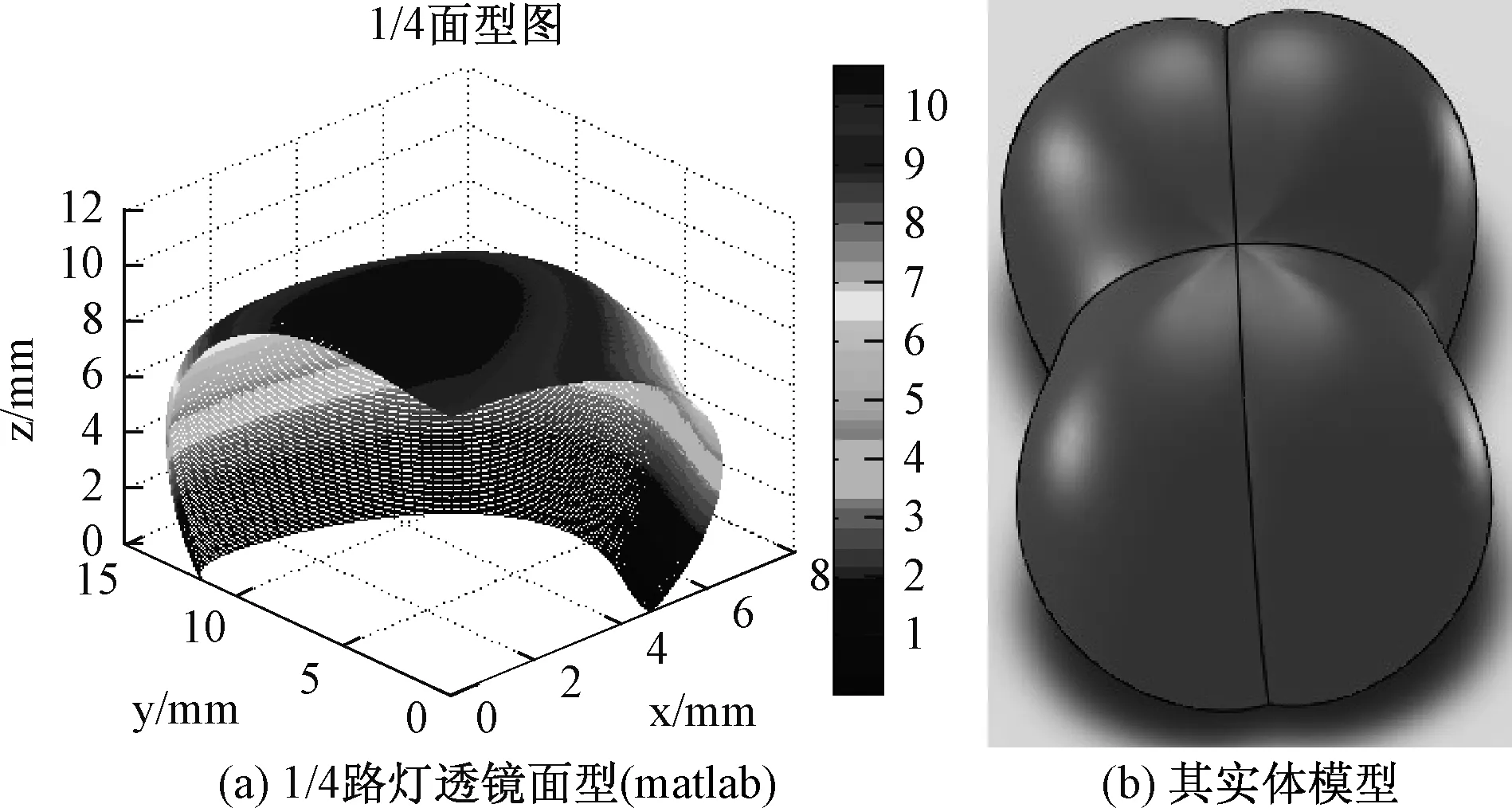
图3 路灯透镜模型Fig.3 Model of road lamp lens

将所得透镜模型导入到Tracepro光学仿真软件中进行系统仿真分析，采用朗伯体光源，发光面尺寸SLED=1.3mm×1.3mm，对该透镜而言可视为点光源，光通量设为100lm，光线为50万条进行追迹，仿真结果如图4所示。

由仿真结果知，有效照明区域基本呈矩形分布，约37m×15m，即道路方向和垂直道路方向上配光角分别约122°和74°，且其照度均匀度分别U∥约为

图4 基于1.3mm×1.3mm点光源的仿真照度图和光强分布图Fig.4 Illuminance distribution & Intensity distribution of the system based on 1.3mm×1.3mm point source

84%和U⊥约为92%，整个区域照度均匀度Uall也在85%以上，且被照面接收的光通量为89.2lm，即能量利用率E=89.2%。由于放样和计算过程不可避免地带入些许误差，至其在对角方向上出现最大值，但其值仅仅比平均值高出约1%，对均匀度的影响几乎可以忽略。

2.2 适用性分析

为比较本方法与网格法的优劣，用图3(b)透镜和基于网格法的“花生米”透镜(中心高10mm)分别对点光源系统(SLED=1.3mm×1.3mm)和面光源系统(SLED=6.5mm×6.5mm)配光，并比较前后的配光效果，效果如图5所示。结果显示，图3(b)透镜对于点光源和面光源系统配光后，照明效果均较好，二者有效照明区域前后变化较小，且Uall均在80%以上；而“花生米”透镜对点光源和面光源系统配光后，尽管前者的配光效果也较好(Uall>80%)，但是，后者的有效照明区域明显缩小(缩小近一半)，且Uall也明显降低，效果明显较差。因此，相对基于网格法而言，基于本文方法得到的透镜对光源系统配光时，光源尺寸对配光效果的影响程度要小得多，这也使得基于此方法的透镜，更具有实用价值。

图5 与“花生米”透镜的配光效果比较Fig.5 Compared with “peanuts”lens in the light distribution effect

2.3 照明方案分析

因单颗光源能量有限，这里灯具采用50颗5×10式透镜模组〔图6(a)〕，单颗光通量100lm的LED光源(1.3mm×1.3mm)，将上述光强分布的.ies文件导入场景仿真软件DIALux中，设置双柏油路面共有6机动车道、2非机动车道和中间隔离带，共16m宽，路灯模组以双列并排式安装，安装高度为10m，其模拟效果如图6(b)所示。

图6 透镜模组及道路照明效果Fig.6 Lens modular and the road lighting effect

图7等照度图显示路面最小照度、最大照度、平均照度分别为6.37lx、9.91lx、7.67lx，均匀度0.83，且路边边缘也有一定亮度，因此周边照度系数为1，均符合《标准》要求。

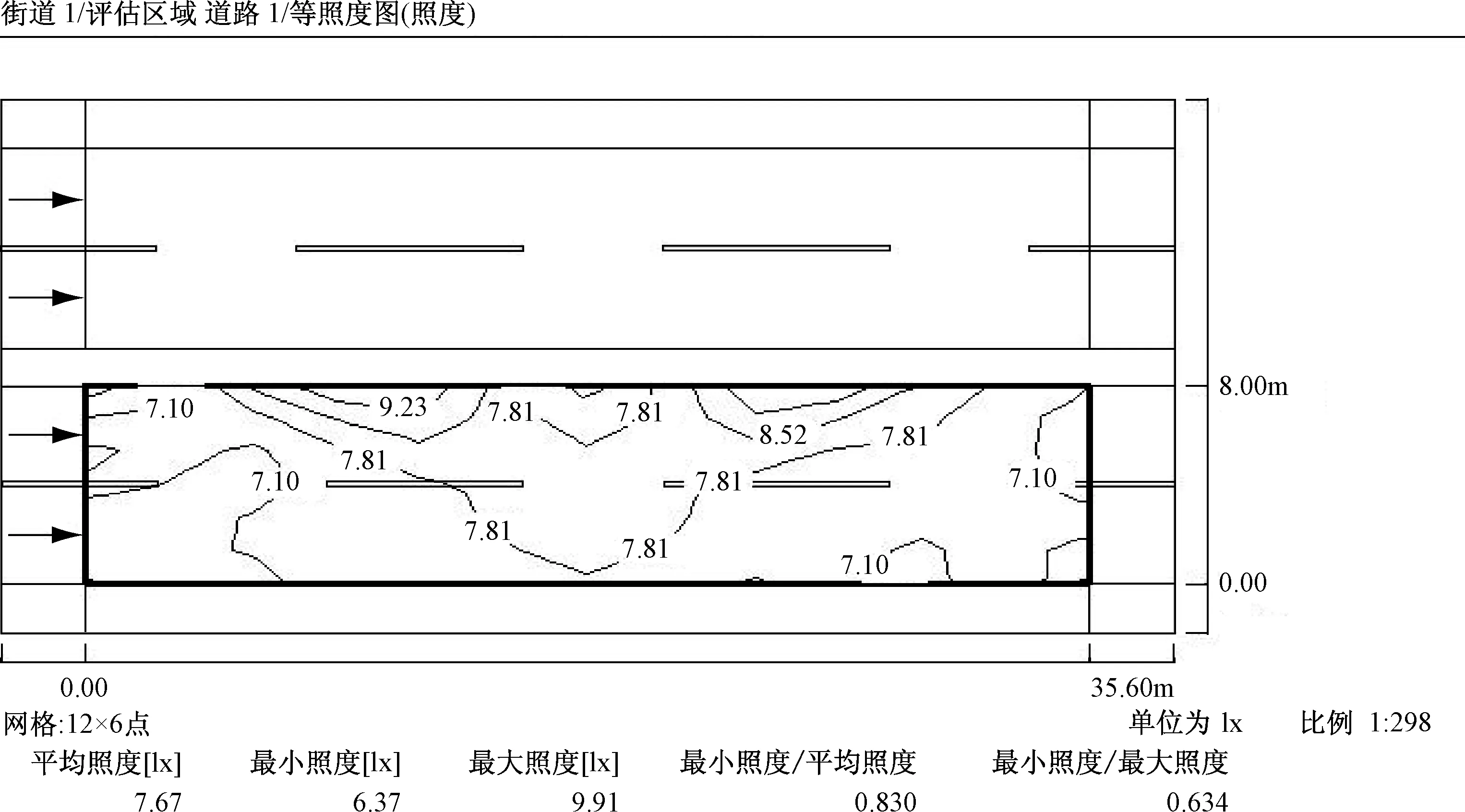
图7 路面的等照度图Fig.7 Equiluminous on road surface

3 结论

本文运用偏微分方程法解决LED道路照明复杂的二次配光问题，充分利用光源空间和被照面间的能量映射关系，结合Snell定律和微分几何原理建立透镜模型的偏微分方程，基于Lax-Wendroff差分格式数值求解自由曲面面型，且所建透镜配光范围和尺寸可根据需要自由设定。建立的透镜模型在Tracepro中对LED照明系统仿真。结果显示，10m远处得到的矩形照明区域，与预设范围吻合度很高，且整体均匀度优于0.85，能量利用率高达89.2%；在对LED扩展光源照明系统配光时，其被照区域和整体均匀度(>0.80)均未见明显减小，较基于网格法的“花生米”透镜，基于本文方法的透镜对LED照明系统配光时，对光源尺寸要求要宽松得多，因此，可适用性更广。用所得透镜组成的5×10式模组路灯系统在DIALux中模拟实际道路照明情形，结果显示路面的均匀度为0.83，周边照度系数为1，均高于《城市道路照明设计标准》要求。因此，本方案在保持偏微分方程法精度高，速度快等优势的同时，也解决了偏微分方程法的可解性问题，且降低了设计难度和复杂度，增加了结果的通用性，这对提高LED在道路照明上的应用水平具有现实的参考意义。

[1] 赖伟, 陈伟民, 刘显明, 等. 自由曲面光学系统设计中目标面照度分布的优化[J]. 照明工程学报, 2012, 22(6): 82-87.

[2] 汪飞佳. LED 路灯目前存在的问题及未来的发展前景[J]. 照明工程学报, 2012, 23(4): 97-99.

[3] 蒋金波， 杜雪， 李荣彬. LED路灯透镜的二次光学设计介绍[J]. 照明工程学报， 2008， 19(4): 59-65.

[4] 吴仍茂， 屠大维， 黄志华, 等. LED照明系统的光照均匀性设计[J]. 光学技术, 2009, 35(1): 74-76.

[5] 芦佳宁，余杰，童玉珍，等. 实现大范围均匀照明的LED透镜二次光学设计[J]. 半导体光电, 2012, 33(3): 334-337.

[6] Jacobson B A， Gengelbach R D. Lens for uniform LED illumination: an example of automated optimization using Monte Carlo ray-tracing of an LED source[C]//International Symposium on Optical Science and Technology. International Society for Optics and Photonics， 2001: 121-128.

[7] Parkyn B， Pelka D. Free-form illumination lenses designed by a pseudo-rectangular lawnmower algorithm[C]//Optics & Photonics. International Society for Optics and Photonics， 2006: 633808-633808-7.

[8] Ries H，Muschaweck J. Tailored freeform optical surfaces[J]. JOSA A， 2002， 19(3): 590-595.

[9] CJJ 45—2006城市道路照明设计标准 [S].中华人民共和国建设部， 2006.

[10] 史永胜，买迪，宁磊. 实现道路均匀照明的LED自由曲面透镜设计方法综述[J]. 照明工程学报， 2010， 21(5): 73-77.

[11] 杨光. LED道路灯具模块化的设计及应用[J]. 中国照明电器，2013 (002): 20-23.

[12] 徐长发，李红. 偏微分方程数值解法[M]. 华中理工大学出版社，2000.