基于T I N的土石方计算研究
2014-04-04徐朱,方强,翟辉
徐 朱,方 强,翟 辉
(江苏省地质调查研究院,江苏南京 210018)
0 引言
近年来,随着国民经济不断发展,各种工程项目越来越多,土石方计算越来越频繁,而土石方量的计算对工程投资估算、工程量大小估算以及工程进度控制都能提供可靠依据。为了使工程技术人员脱离繁复的土方量手工计算,通过专家学者的不断研究,率先在AutoCAD基础上开发出了一系列成熟方法和程序,大大减轻了工程技术人员工作负担,提高了计算速度。地理信息系统的出现,各种空间分析方法和手段的引入,使复杂的传统空间分析任务变得更加简单易行,特别是在ArcGIS中克立格插值[1,2]空间插值方法的帮助下,精确的TIN模型能快速模拟地面特征,使土方量计算的操作更加简便、精度日益提高。
1 土方量计算的原理和方法
1.1 土方量计算的原理
土方量计算其实就是求取设计地面和自然地面之间物质的体积差。设计地面是按规则设计出来的,容易准确表达。而自然地面是由无数个点组成,人工采集的只能是有限的数据,表达自然地面特征也只能是无限的接近。假定自然地面是连续和渐变的,通过获取有限的数据,也能模拟和近似表达真实的地面,微积分就是一种描述连续变化的方法[3,4],土石方的计算就是借鉴了微积分的思维方法,将地形分成若干微小单元,并将其地形特征简化,以采集数据或空间插值数据近似表达各个单元的地形特征,分别计算各个微小单元的体积差,然后汇总求和,就得到了最后的土方量。这里也只是借用了微积分的思维方法,而不是具体运算程序,下一步是土石方计算的原理,如图1所示。

图1 土石方计算的原理
1.2 基于TIN的体积算法[5]
不规则三角网(TIN)是DEM的主要表现形式[6],是按照一定的规则将按地形特征采集的离散点连接成覆盖整个区域的互不重叠的三角形,能很好地逼近原始地形表面,从而更好地表达真实的地面特征。基于TIN算法的土方量计算一般采用三棱柱法,利用场底和场顶之间的标高差建立三角网模型,然后利用泰森三角形的原理,把这个三角网模型分成若干个不规则的三棱柱,一个平面内,三点平均,从而计算三棱柱的体积,最后再将这若干个三棱柱加到一起,就是我们所求取的总的土石方量(填方量和挖方量)。
三棱柱法是沿地形等高线将每个方格的对角点连接起来划分为两个等腰直角三角形,根据各角点施工高度符号的不同,零线(即方格边上施工高度为零、不填不挖的点的连线)可能将三角形划分为两种情况:三角形全部为挖方或全部为填方以及部分挖方和部分填方。
三棱柱法的计算公式是根据立体几何体积计算公式推导出来的,比较精确。其计算方法如下:
下一步是全挖或全填的体积公式,如图2所示:

上述公式(1)中,a是方格的边长(m);h1、h2、h3是三角形各角点的施工高度(m)。
当划分方格为部分挖方和部分填方时,零线将三角形划分成底面为三角形的锥体和底面为四边形的槭体,下一步是三棱柱法,如图3所示。
锥体的体积为
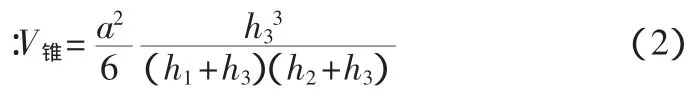
槭体的体积为

上述公式(2)、(3)中,V锥是锥体的体积(挖方或填方)(m3);V槭是槭体的体积(挖方或填方)(m3);h1、h2、h3是三角形各角点的施工高度(均用绝对值代入),但h3常指锥体顶点的施工高度(m)。

图2 三棱柱法(全填或全挖)
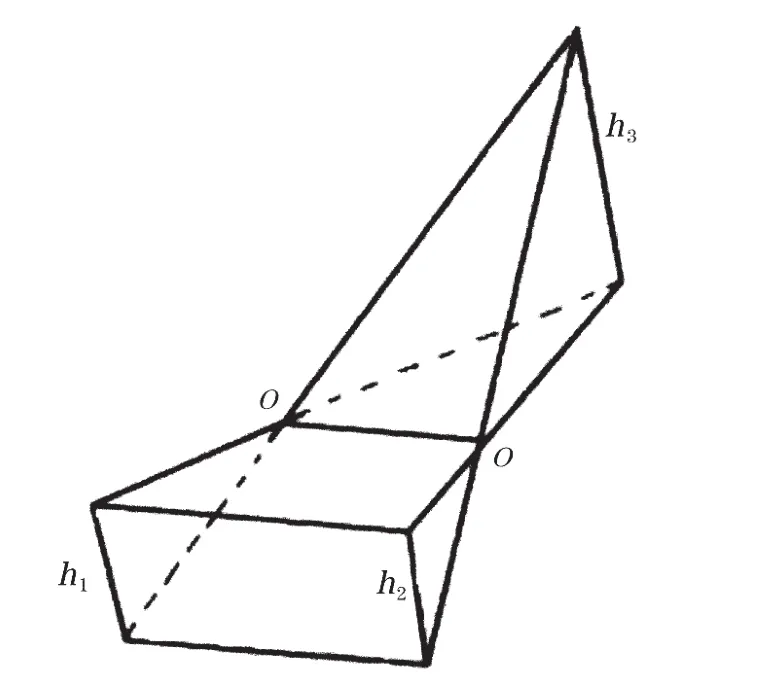
图3 三棱柱法(部分填方和部分挖方)
2 实现步骤
在ArcGIS中,为了计算土方量,需要将设计地面和自然地面进行叠加,叠加后形成的交线就是回填区和开挖区的分界线。通过计算每一条分界线围成的封闭区域的体积,就得到了每一个回填区和开挖区的体积,即为所求区域的填方量和挖方量。下一步是基于TIN的土方量计算流程,如图4所示。
2.1 数据准备
土方量计算前首先准备高程点、等高线等数据,由于其格式一般是CAD的dwg格式,需要通过数据转换,形成ArcGIS需要的Shapefile格式。
2.2 数据检查
查看高程点、等高线的属性数据中是否有高程字段并且高程字段非空。
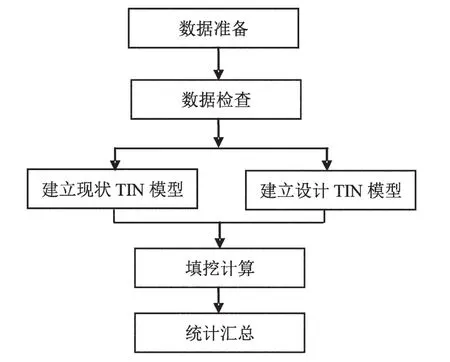
图4 基于TIN的土方量计算流程图
2.3 生成TIN模型
在ArcGIS中,使用3D Analyst模块,选择高程点和等高线数据通过克立格空间插值[7]进行TIN模型构建。需要注意的是,要先选择好存放高程值的字段。根据设计前后地形,分别生成 TIN1和TIN2。
2.4 填挖计算
利用Cut/Fill工具对TIN文件进行填挖计算,最后会生成一个图层,图层上分色显示回填区和开挖区的范围。
2.5 统计汇总
生成的图层属性表中,正值表示要填充的土方量,负值表示要挖掉的土方量,通过统计,即可分别计算出填方量和挖方量。
3 工程实例分析
笔者参与了连云港市某废弃矿山土地整治土石方计算工作,该地区地表凹凸不平,最低处高程66m,最高处高程100m,根据整治设计目标,采用了ArcGIS进行土方量计算。
3.1 数据获取
收集该整治区的高程点、等高线数据,特别在地面起伏处,利用全站仪补测高程点数据,增加采集点密度,并将实测点输入计算机。
3.2 TIN模型建立
利用ArcGIS系统的3D分析模块根据现状图和设计图中高程点、等高线数据按照10m×10m栅格单元进行插值,下一步是最后分别生成现状TIN和设计TIN,如图5和图6所示。
3.3 计算工程填挖方
根据生成的设计前、后TIN表面,利用3D分析模块下的Cut/Fill工具生成一个新的图层,下一步计算产生的填挖方栅格图,如图7所示,该图层的右下角图例中,Net Gain表示净填方,Net Loss表示净挖方,Unchanged表示不填不挖。
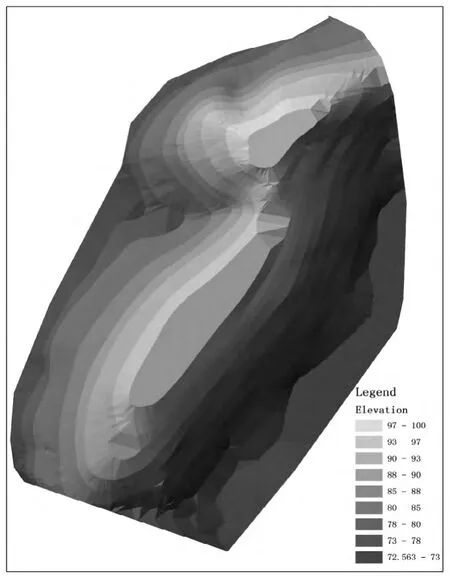
图5 现状TIN(按高程分类显示)

图6 设计TIN(按高程分类显示)

图7 计算产生的填挖方栅格图

表1 工程填挖方统计表
下一步是打开该栅格要素属性表,如表1所示,其中表内字段Volume值大于零的表示净填方,小于零的表示净挖方,等于零的不填不挖,通过鼠标右键点击Volume字段,可以统计栅格体积,总计为72 269,填方大于挖方。
4 结论与建议
基于TIN的土石方计算,是通过设计前后地形模型叠加找出回填区和开挖区的分界线,再对每一个封闭区域通过求取体积差来统计每一个回填区和开挖区的土方量,最后统计汇总得出总土方量的一种方法。相比其他传统土方量计算方法,其计算简单、快速,自动化程度高,适用于各种地形,特别是复杂地形。
因此,在应用TIN模型计算土方过程中有如下建议:①前期对数据进行检查,高程字段非空,否则将产生错误;②生成的现状TIN和设计TIN范围应保持一致;③优先选择闭合等高线参与TIN模型建立。
该方法对基础数据要求较高,计算精度跟地形、坡度及栅格大小等因素有关,一般情况下,栅格越小,精度越高。这种方法简单、可靠,适用范围较广,可推广性较强。
[1]俞志新,李艳,黄明祥.地统计克立格插值法在工程土方计算中的应用[J].浙江水利科技,2003(4):37-38,47.
[2]陈勇.利用ArcGIS地统计分析进行土地平整土方量计算的研究[J].安徽农业科学,2007(1):70-71,103.
[3]程不时.突变论及其应用[J].科学通报,1978(9):513-522.
[4]欣欣.突变论模型[J].哲学动态,1990(2):20-21.
[5]周启鸣,刘学军.数字地形分析[M].北京:科学出版社,2006.
[6]THOMPAONJA,BELLJC,BUTLERCA.Digital Elevation Model Resolution:effect on terrainattribute calculation and quantitative sail landscape modeling[J].Geoderma 2001(1).
[7]汤国安,杨昕.ArcGIS地理信息系统空间分析试验教程[M].北京:科学出版社,2006.
