基于逆系统的三自由度直升机内模控制设计

于春海，潘 丰

YU Chunhai,PAN Feng

江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122

Key Laboratory of Advanced Process Control for Light Industry（Ministry of Education）,Jiangnan University,Wuxi,Jiangsu 214122,China

1 引言

三自由度直升机模型系统是一种典型的非线性、高阶次、多变量、强耦合的多输入多输出系统[1]。传统的PD控制[2]、PID控制[3]以及目前比较成熟的LQR控制[4]等只能较好地实现位置的跟踪，但在调节时间和超调量等方面控制效果不尽人意。另外还有许多学者也提出了很多新的方法，例如模糊控制[5]、自适应控制[6]以及预测控制[7]等，这些方法虽然在很大程度上改善了系统的控制效果，但没有实现解耦控制。

近年来，逆系统方法已经在非线性系统的线性化去耦合方面得到应用，因此本文提出采用内模控制和逆系统结合的方法实现对三自由度直升机模型系统的控制，通过采用神经网络方法获得原模型的逆模型，使被控对象转变为一个标准的具有线性关系的系统，结合反馈补偿实现解耦[8-9]。

2 三自由度直升机的数学模型

三自由度直升机模型系统是一个欠驱动的模型系统，它的动力主要来源于后端的两个推进器。推进器的动力大小与电压成正比，关系如下式：

式中kc为比例常数。

根据系统的特点，三自由度直升机模型可分三个轴来描述，分别为：高度轴、横侧轴、旋转轴。三个轴的模型分别如式（2）～（4）所示[1，6，10]。图 1为直升机模型的空间坐标系示意图。

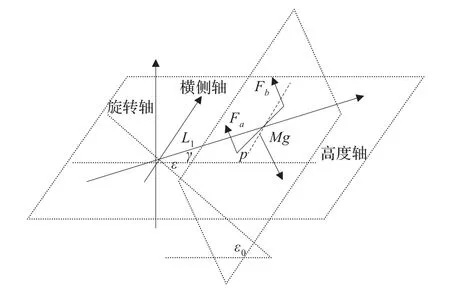
图1 直升机模型的空间坐标系示意图

本文中涉及到了变量及常量含义：

M为直升机模型的有效质量；g为重力加速度；Mg为直升机模型的有效重力值；L1为电机与支点的距离；LP为每个电机与横侧轴的距离；ε为高度角；p为横侧角；γ为旋转角速度；ε0为高度角的初始值。

（1）高度轴：高度轴的转矩是由前后两个电机产生的升力Fa和Fb之和产生的，当升力大于重力Mg时，直升机上升；反之下降。根据动力学原理可得关系如下：

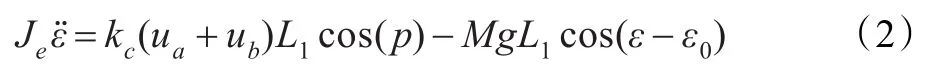
其中，Je为俯仰轴的转动惯量，ε¨为俯仰轴的旋转加速度，ua和ub为前后电机的电压，Fa和Fb分别为前后两个电机产生的升力。

（2）横侧轴：横侧轴由两个螺旋桨电机产生的升力控制，如果Fa产生的升力大于（或小于）Fb产生的升力，这样就会产生一个侧向力，使直升机围绕基座正向（或反向）旋转。其动力学方程为：

其中，Jp为横侧轴的转动惯量，p¨为横侧轴的旋转加速度。

（3）旋转轴：旋转轴的动力来源是螺旋桨横侧轴倾斜时产生的水平方向升力，对于比较小的横侧角，这个力需要使直升机在空中保持平衡，大约为Mg。Mg的水平分量会对旋转轴产生一个力矩，旋转轴由这个力产生旋转加速度，其动力学方程为：

其中，Jt为旋转轴的转动惯量，γ˙为旋转角加速度。

由式（2）～（4）可以看出，三自由度直升机模型系统是一种典型的非线性、高阶次、多变量、强耦合的多输入多输出系统。

3 RBF神经网络逆控制系统

3.1 直升机模型系统的可逆性分析

三自由度直升机系统是一个典型的MIMO系统，系统的状态 量 X=[x1x2x3x4x5]=[ε p ε˙p˙γ]T，控制量U=[uaub]，输出量Y=[y1y2]=[ε p]，因此直升机系统的状态空间模型如下：

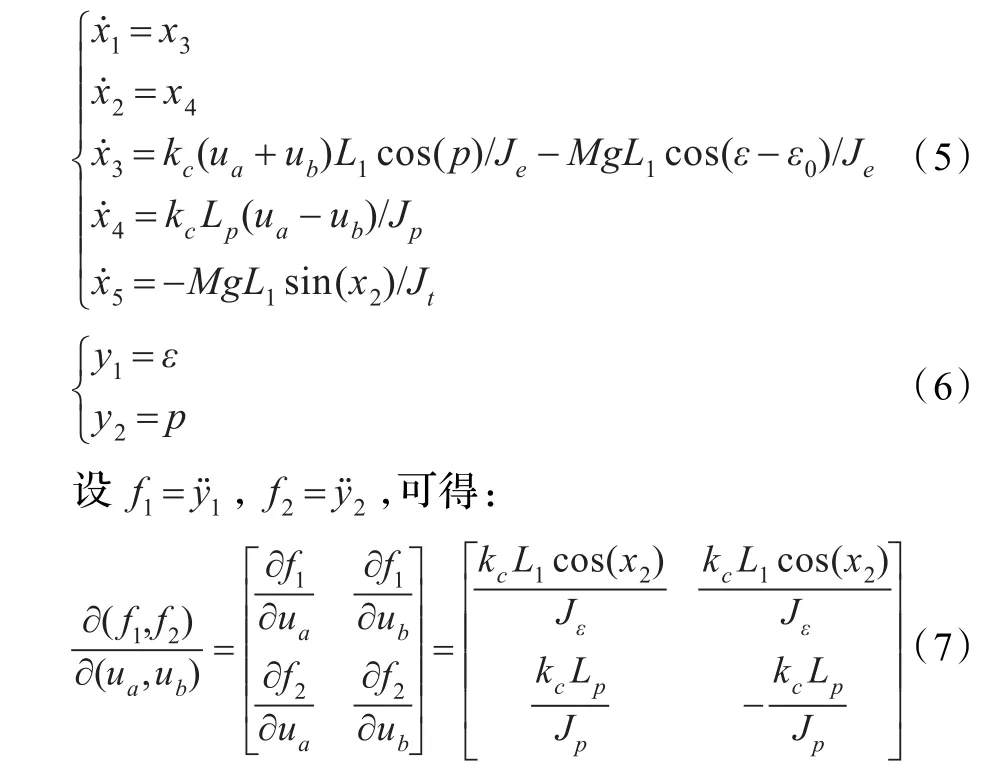
若横侧角过大，会影响直升机飞行的高度。通常考虑人的乘坐舒适，横侧角不宜过大，常取0≤p≤45°，所以有：

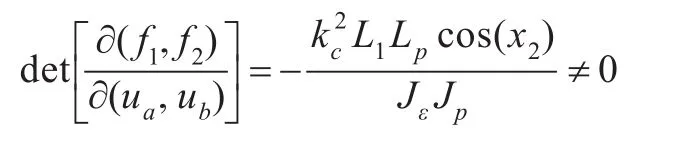
其中x2=p。

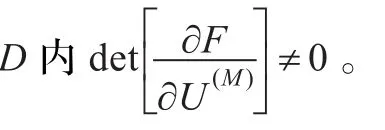
因此，可知直升机系统的逆系统是存在的并且逆系统可以表示为：

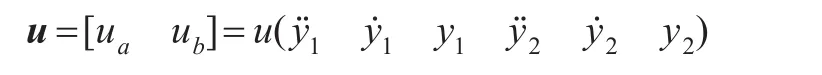
但是基于几何方法来获得系统的逆模型是很困难的，所以本文利用神经网络对任意连续函数很强的逼近能力来构建系统的逆系统，同时也可将一个多入多出、强耦合的非线性系统转化为几个相对独立的单入单出的线性系统。

3.2 直升机系统的逆模型的确定

本文采用图2所示结构来确定直升机系统的逆模型。

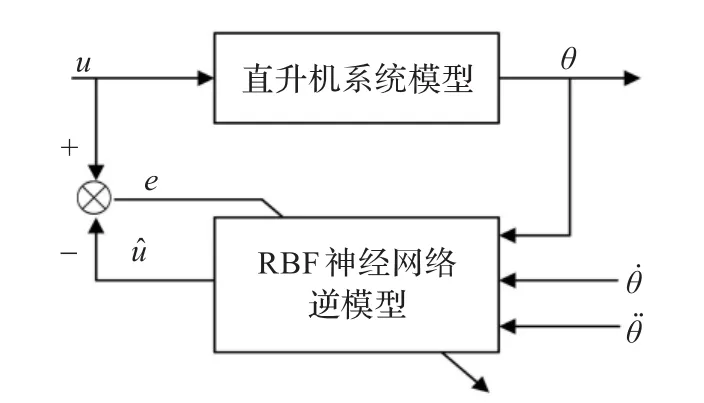
图2 直升机系统逆模型确定结构图

如图2所示，在该并联型逆模型辨识结构中，用于辨识的神经网络为RBF神经网络，θ是高度角或横侧角，直升机模型的输入为u，RBF神经网路的输入为(θ θ˙θ¨)，神经网络的输出为 u^。当神经网络逆模型被训练完成时，即输出u^充分接近直升机模型的输入u，换句话说此时的偏差e接近于0，其输入输出特性和直升机动力学模型的逆特性相同。可认为该逆模型精确。

取神经网络逆模型的误差函数：

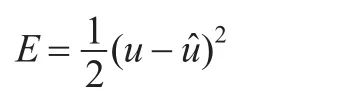
3.3 基于RBF神经网络逆模型的去耦控制

如图3所示，εd和 pd为控制系统的给定值，ε和 p为系统的实际输出。在系统的运行过程中，基于RBF的神经网络逆模型中的实时参数传递给神经网络控制器，这就使得 M*C=I恒成立[9，11]。也就是说，三自由度直升机模型可以看做为一个伪线性系统，这就完成了将一个复杂的非线性耦合系统转换为两个相对独立的伪线性系统[12-13]。如图4所示。

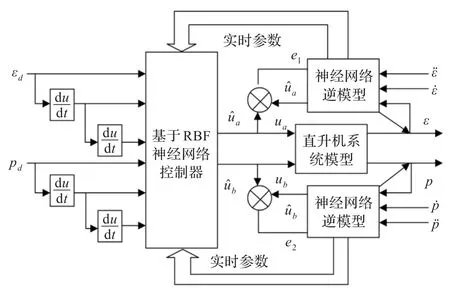
图3 RBF神经网络去耦控制框图

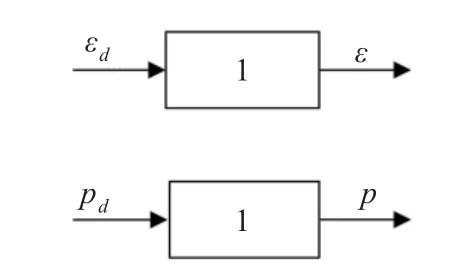
图4 伪线性模型框图

3.4 控制系统设计

利用RBF神经网络求出原系统的逆系统，即系统的逆模型。并将它串连在原系统之前，从而构成了基本线性化的伪线性系统，理论上讲，伪线性系统的输出严格跟踪它的输入。然而，伪线性系统相对于被控过程来说是开环控制结构，实际当中将不可避免地存在建模误差及外界扰动，这些因素都会导致不同程度的跟踪偏差。为了补偿建模误差及外界扰动造成的跟踪偏差，应当对伪线性系统进行反馈控制。

内模控制是一种基于系统内部模型和反馈校正的预测控制[14]，是一种重要的控制结构，与常规反馈控制理论相比有稳定、完全可控、无静差等特点，能获得良好的动态响应，同时也能兼顾鲁棒性和稳定性，且内模控制器的参数在线调节非常方便。因此，为了补偿这些误差，把伪线性系统作为被控对象，引入内模控制策略对它进行控制，结构如图5所示。

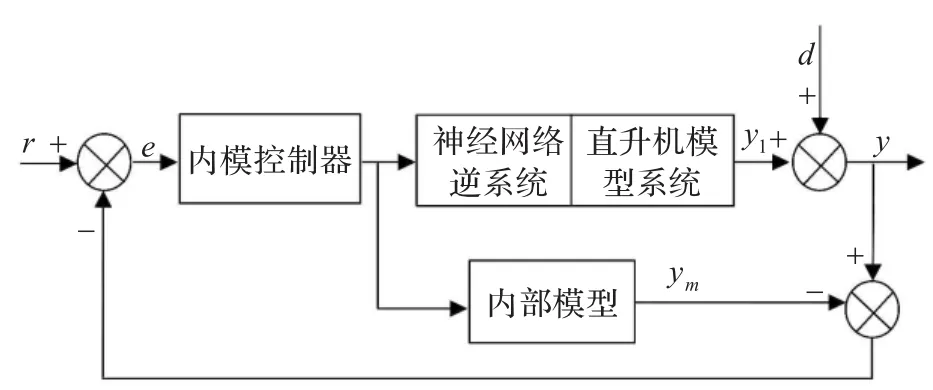
图5 内模控制结构框图

在本文中，针对高度轴和横侧轴，采用内模控制方法，设计了两个内模控制器。系统控制框图如图5所示。

图5中r为系统的输入角度（高度角或者横侧角），y是控制系统的输出，y1为伪线性系统的输出，ym为内模输出，d是干扰。

4 系统实验及分析

神经网络控制器和系统逆模型的选择是采用单隐层RBF神经网络，模型是N3∶6∶1网络。根据梯度下降法，神经网络逆模型的参数被精确到E≤0.001。

选择内部模型Gm(s)=1，内模控制器当干扰d(s)=0时，闭环系统的误差表达式为：

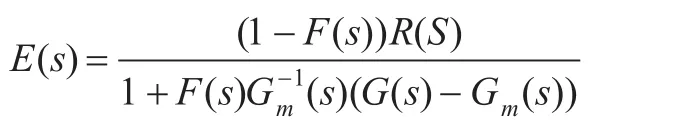
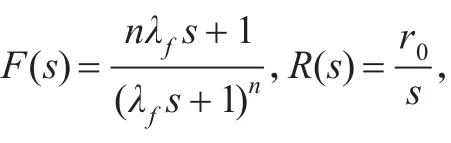
仿真结果与Quanser公司提供的LQR方法对比显示[1，15]，本文的方法具有很好的跟踪效果，不仅响应时间优于LQR方法，特别是在超调方面，基于LQR方法的输出曲线具有明显的超调约20%，而本文提出的方法几乎无超调。证明了该方法的有效性。

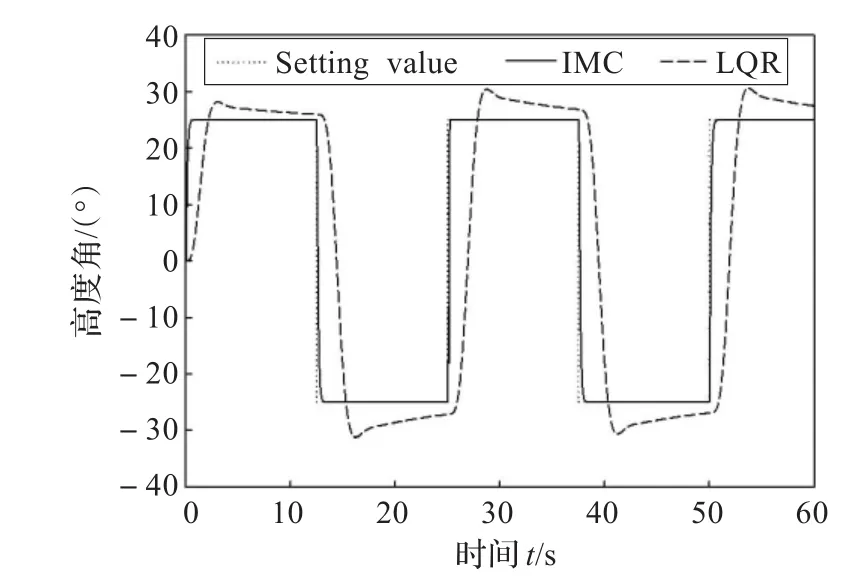
图6 高度角跟踪效果对比图

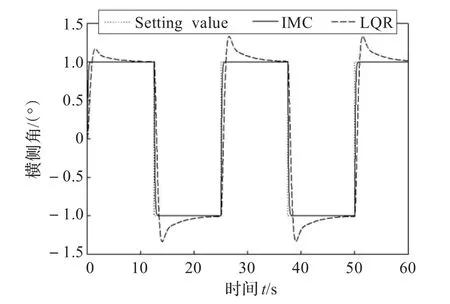
图7 横侧角跟踪效果对比图

5 直升机系统的实际控制

MATLAB与实时控制软件WinCon相结合构成了三自由度直升机模型的软件系统。现将用该控制器来控制三自由度直升机模型系统。连接好各种控制信号线，通过Simulink和WinCon软件控制模型系统。图8和图9是控制的实时曲线图。

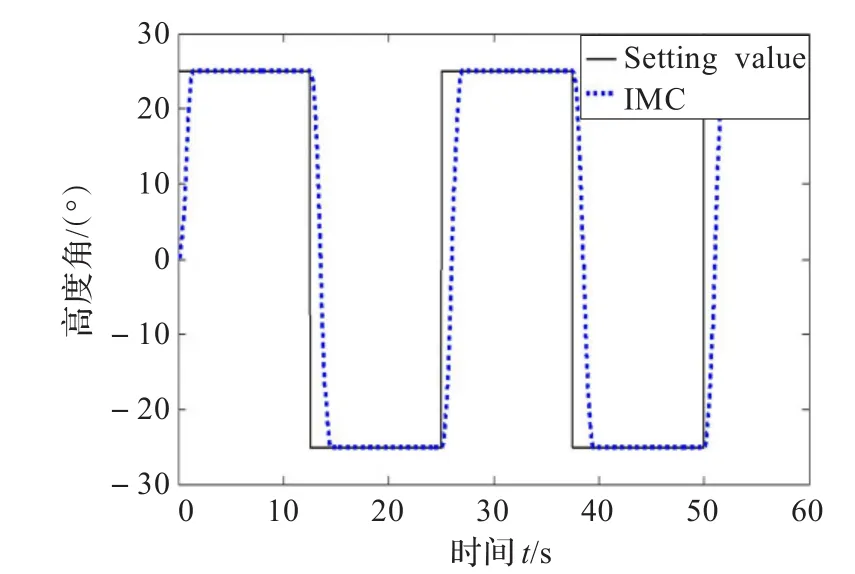
图8 高度角实时曲线

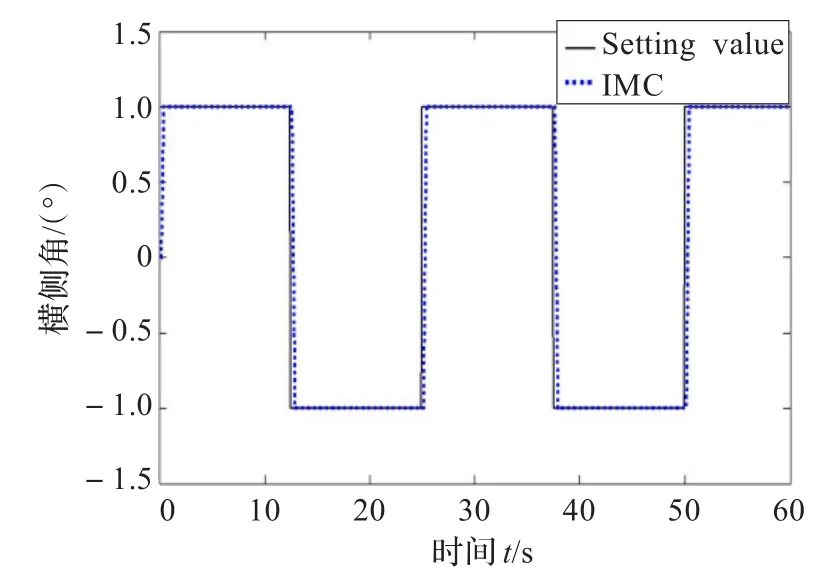
图9 横侧角实时曲线

图8给出了高度角的实物控制曲线，在实际控制过程中，给定的目标位置为25°，从曲线中可以看出，超调几乎为零，调节时间约1.8 s。

图9给出了横侧角的实物控制曲线，在实际控制过程中，给定的目标位置为1°，从曲线中可以看出，超调量几乎为零，调节时间约1.2 s。

由图8和图9可知该控制器应用在直升机系统模型上进行半实物仿真的效果较好，证明了该方法的可行性。

6 结论

本文采用内模控制与逆系统结合的方法对三自由度直升机系统进行跟踪控制，控制器和系统逆模型的确定采用了相同的神经网络，因此能够较好地实现三自由度直升机模型的动态解耦并使其转化为两个SISO的伪线性系统。由于去耦合的系统不包含原系统的参数，这就大大增强了系统的鲁棒性。此外，控制器的设计采用内模控制可以避免由于外来干扰引起的误差，提高了系统的抗干扰能力。MATLAB仿真结果显示，本文的方法得到了更好的控制效果。同时半实物仿真效果表明该方法的可行性，具有一定的工程应用价值。

[1]Quanser Consulting.3-DOF helicopter reference manual[Z].Canada：Quanser Inc，2009.

[2]Dong Xiucheng，Zhao Xiaoxiao，Shu Mei.Research of control method based on 3-DOF twin rotor MIMO system[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation，Chongqing，China，2008：3279-3283.

[3]Ahmand S M，Chipper field A J，Tokhi M O.Modeling and control of twin rotor MIMI system[C]//Proceedings of the American Control Conference，2000：1720-1724.

[4]郭亮，余祖龙.三自由度直升机LQR控制器设计与仿真[J].科技资讯，2011（36）：29-30.

[5]Liu Zhichao，Shi Hongbo.Control strategy design based on fuzzy logic and LQR for 3-DOF helicopter model[C]//International Conference on Intelligent Control and Information Processing，Dalian，China，2010.

[6]Orlov Y，Aguilar L T.Stabilization of a 3-DOF underactuated helicopter prototype：second order sliding model algorithm synthesis，stability analysis，and numerical verification[C]//12th IEEE Workshop on Variable Structure Systems，VSS’12，Mumbai，2012.

[7]Witt J，Boon S，Wemer H.Approximate model predictive control of a 3-DOF helicopter[C]//Proc of the 46th IEEE Conference on Decision and Control，LA，USA，2007：4501-4506.

[8]陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，2003：69-82.

[9]戴先中.多变量非线性系统的神经网络逆控制方法[M].北京：科学出版社，2005：59-79.

[10]赵笑笑，董秀成.基于LQR最优调节器的三自由度直升机控制系统[J].自动化信息，2005（9）.

[11]Dai X，He D，Zhang X.MIMO system invertibility and decoupling control strategies based on ANN αth-order inversion[C]//IEE Proc Control Theory Appl，2001，148（2）：125-136.

[12]Han Xiongli，Hua Deng.An approximate internal modelbased neural control for unknown nonlinear discrete processes[C]//IEE Trans on Neural Networks，2006，17（3）：659-671.

[13]魏东.非线性系统的神经网络参数预测及控制[M].北京：机械工业出版社，2008：25-32.

[14]戴文战，丁良，杨爱萍.内模控制研究进展[J].控制工程，2011，18（4）：487-492.

[15]樊京，刘叔军，盖晓华，等.MATLAB控制系统应用与实例[M].北京：清华大学出版社，2008：162-178.