FR共轭梯度法与泰勒级数展开法协同定位算法
2014-04-03
(河北联合大学电气工程学院,河北 唐山 063009)
0 引言
在无线定位应用广泛的今天,射频识别(radio frequency identification,RFID)由于其非视距识别以及低成本的优点,被广泛应用于室内定位。通过物理测量得到标签与读写器之间的距离或角度的定位算法包括:到达时间法、到达时间差法、到达角法、接收信号强度法(received signal strength indication,RSSI)。在这四种方法中,到达时间法和RSSI比较常用。但由于到达时间法硬件要求太高,所以RFID定位系统中多采用RSSI[1]。
基于RSSI的无线射频识别技术(RFID)是在已知发射功率的情况下,读写器测量接收功率,使用理论或经验的信号传播损耗转化为距离。在获得各个读写器到待测标签的距离之后,根据标签到各读写器的差值建立一组双曲线方程。由于方程具有非线性,需要将其转化为线性方程后求解[2]。在线性化方程的求解过程中,应用泰勒级数展开法,由于其具有很高的定位精度,在初始估计位置和实际位置相接近的情况下,可以得到较精确的定位结果;但在初始位置偏差较大的情况下,算法的收敛性难以保证[3]。为了确保定位结果的收敛性,本文采用FR共轭梯度法进行初始位置的计算[4]。
1 基于RSSI的定位算法
RSSI定位算法首先需要建立待测标签环境的距离-损耗模型,然后设定已知读写器的参考位置。通过测量对比信号发射端与接收端的信号衰减情况来计算两者之间的距离,设置多个读写器便可利用三边或多边定位法来完成对待测标签的定位[5]。
电磁信号在室内空间传播的过程中,会受到墙壁、障碍物等影响,产生能量损耗与衰减。这种因外界环境引起的衰减与电磁波发射与接收过程中所传播的距离有直接的关系。RSSI采用的信号距离-损耗模型一般为对数距离衰减模型,其表达式为:
(1)
式中:d为发射机和接收机之间的距离;do为参考距离;η为信道衰减指数,一般取值2~4;Xσ为均值为零、均方差为σ的高斯随机噪声变量;P(do)为距离发射机do处的信号强度;P(d)为距离发射机d处的信号强度;P(do)可以通过经验得出,通过信号强度P(d)求出距离d[6]。
如果四个读写器参与定位,则使用双曲线模式建立方程组。根据对数距离衰减模型得到待定位标签到各个读写器的距离后,可建立方程:
Di,1=Di-D1
(2)
(3)
如果三个读写器参与定位,则使用圆周模型建立方程:
(4)
式中:(Xi,Yi)为读写器坐标;(x,y)为待测标签坐标;Ri为读写器与标签之间的距离;N为参与定位的读写器数目。
式(2)的求解过程为求解非线性方程组,求解非线性方程组相当于无约束非线性最优化问题,非线性问题需要进行线性化处理[7]。
FR共轭梯度法是由线性问题发展而来的求解无约束非线性最优化问题的方法。其具有二次终止性,计算量小,因而得到广泛应用。将FR共轭槽度法与泰勒级数展开算法相结合,可有效提高定位精度,保证定位的准确性[8]。
2 泰勒级数展开法
以下为四个读写器参与定位时,所建立的方程组通过泰勒级数展开法求解的过程。
根据式(2)定义函数:

假设(x0,y0)为待定位标签位置坐标的初始值:
x=x0+δxy=y0+δy
(5)
采用泰勒级数展开,仅保留前两项可得:
(6)
(7)
式(6)可以写为:
Aδ=D+e
(8)
令:
(9)
(10)
(11)
(12)
对于式(8)的加权最小二乘的解为:
δ=[ATR-1A]-1ATR-1D
(13)
令:
如果δz>10,则算法发散;如果δz<0.000 1,则算法收敛,停止计算,输出定位结果。
3 FR共轭梯度法
首先将si(x,y)计算式改写成:
ψi(x,y)=si(x,y)-di,1+εi,1i=2,…,N
(14)
使用FR共轭梯度法对式(14)构造模函数:
(15)
FR共轭梯度法将共轭性和最速下降方向相结合,利用已知迭代点处的梯度方向构造一组共轭方向,并沿此方向进行搜索,求出函数极小点。
设算法中所使用的各估计点为wk,对应的坐标为(xk,yk),k=0,1,……。函数Ψ(x,y)在一点的梯度方向为G,-G即为最速下降方向[9]。在FR共轭梯度法中,第一个搜索方向取最速下降方向,即d0=-G0,其他搜索方向根据FR共轭梯度法得到:
dk+1=-Gk+1+βkdk
(16)
βk根据FR法计算,即:
(17)
设(x0,y0)为解的一个近似值,从此点开始进行搜索,搜索方向为最速下降方向,即d0=-G0。计算Φ在此点的梯度方向:
G0=(g10,g20)T
(18)
(19)
若‖G0‖<ε,则停止,w0为所求极小点;否则继续计算。
若‖G0‖>ε,沿负梯度方向-G0跨一适当的步长λ0。步长的求取方法采用非精确线性搜索法Armijo准则,即:
(20)
式中:ξ∈(0,1);σ∈(0,0.5);gk为梯度方向;dk为搜索方向,令步长λk=ξmk,其中mk为满足式(19)的最小非负整数。
搜索过程中,由m=0,mk=m开始搜索,wk+1=wk+ξmkdk,如果不等式成立,则停止运算;否则m=m+1,继续运算。
求出的λ0可以使得新的点(x1,y1)为Ψ(x,y)在方向d0上的相对极小值,即:
Ψ(x1,y1)≈min{Ψ(x0-λ0g10,y0-λ0g20)}
(21)
将λ0代入下式:
wk+1=wk+λkdk
(22)
求得w1之后计算G1,若‖G1‖<ε,则停止,w1为所求极小点;否则重复上述过程,直到‖Gk‖足够小为止。
4 改进算法仿真及分析
搜索过程中,首先使用FR共轭梯度法进行搜索定位。在位置比较接近之后,得到初步定位结果。然后使用Taylor级数展开算法对初步定位结果进行精确。
本文使用Matlab进行定位仿真[10],仿真采用四个读写器,读写器的分布以及各个读写器大概的读卡范围如图1所示。
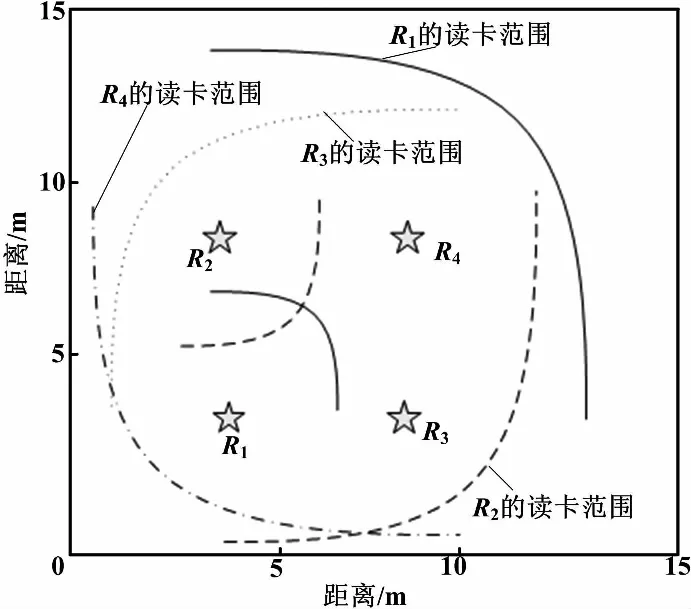
图1 读写器分布图
四个读写器的读卡范围分别为R1(5,5),R2(5,10),R3(10,5),R4(10,10)。
每个读写器的识别距离在10 m以内,在仿真区域的中间部分,四个读写器均参加定位;在比较边缘的位置,三个较近的读写器参与定位。
为了对比改进效果,本文对传统泰勒级数展开法也做了仿真。仿真中协同定位算法和传统泰勒级数展开法的仿真精度均取0.000 1。
根据所有仿真结果,当四个读写器均参加定位的情况下,定位结果受到初始值是否接近真实值,以及所得的测量值是否精确的影响。定位结果可以分为四类。
① 初始值接近真实值,所得的测量值精确,协同定位算法的结果与传统泰勒级数展开法的结果相同。
② 初始值远离真实值,所得的测量值精确,协同定位算法定位结果准确,且收敛情况良好,而传统泰勒级数展开法则不能收敛。
③ 初始值远离真实值,所得的测量值不精确,协同定位算法定位结果较为准确,且收敛情况良好,而传统泰勒级数展开法则不能收敛。
④ 特殊情况为所得的测量值误差较大,无论初始值是否接近真实值,协同定位算法与传统泰勒级数展开法均不收敛,此时定位结果采用FR共轭梯度法的定位结果。
误差采用均方根误差RMSE:
(23)

第二种情况,以真实点(6.3,7.9)为例,如表1所示,协同定位算法解决了传统泰勒级数展开法不收敛的问题。
第四种情况,以真实点(3.3,6.9)为例,如表2所示,协同定位算法与传统泰勒级数展开法均不收敛的问题,采用FR共轭梯度法的定位结果。

表1 初始值远离时定位结果

表2 测量误差较大时定位结果
定位结果分为以下两类。
① 初始值接近真实值,协同定位算法比传统泰勒级数展开法更加精确。
② 初始值远离真实值,协同定位算法定位结果较为准确,且收敛情况良好,而传统泰勒级数展开法则不能收敛。
以上两种情况均以真实点(11.7,13)为例,一号读写器不参与定位。
第一种情况如表3所示,协同定位算法提高了传统泰勒级数展开法的精度。第二种情况如表4所示,协同定位算法解决了传统泰勒级数展开法不收敛的问题。

表3 初始值接近时定位结果

表4 初始值远离时定位结果
5 结束语
分析仿真结果可得,FR共轭梯度法与泰勒级数展开法协同定位算法相结合,有效改进了传统泰勒级数展开法在初始估计值距离真实值差距较大的情况下算法难以收敛的问题。当三个基站参与定位时,协同定位算法提高了定位精度。当三个基站参与定位、测量误差较大的情况下,两种算法均不收敛,可以采用FR共轭梯度法的定位结果,使得协同定位算法具有很强的应用性。
[1] 王保云.物联网技术研究综述[J].电子测量与仪器学报,2009(12):1-7.
[2] 徐加伟,牛清伟.浅谈煤矿井下人员定位系统[J].煤矿开采,2009,14(4):72-74.
[3] 谭民,刘禹,曽隽芳.RFID技术系统工程及应用指南[M].北京:机械工业出版社,2007.
[4] 叶晨成,校景中,肖丽.基于RFID的井下人员定位系统[J].武汉理工大学学报:工学版,2010,32(15):146-149.
[5] 羊红光,邢亚斌,张湃.基于RFID的井下人员定位系统[J].河北省科学院学报,2011,28(4):53-56.
[6] 刘宗元.基于射频识别(RFID)的室内定位系统研究[D].中山:中山大学,2009.
[7] 李俊.基于RFID的室内定位系统的研究和设计[D].成都:电子科技大学,2009.
[8] 薛毅.最优化原理与方法[M].北京:北京工业大学出版社,2001.
[9] 林敏.RFID标签定位技术研究[D].镇江:江苏大学,2007.
[10]樊荣.RFID读写器定位算法研究[D].成都:电子科技大学,2010.
