模糊信息检索法在滑坡预报中的应用

杨 军，王 波，艾 虎，颉 丽，方世跃

(1.甘肃省科学院 地质自然灾害防治研究所，甘肃 兰州 730000；2.中石油西气东输管道公司，陕西 西安 710018；3.西安科技大学 地质与环境学院, 陕西 西安 710054)

滑坡是一种常见的地质灾害，会给工农业生产和人民生命财产造成巨大损失，甚至是毁灭性灾难。如果能够较准确地进行滑坡预报，就可以尽早采取减灾防灾措施，使滑坡灾害造成的损失减少到最低程度[1]。滑坡的发生和发展既受形成条件的控制，又受诱发因素的影响，滑坡预报至今仍是滑坡研究的重点与难点，但是滑坡也有其可预报性，通过对形成条件、诱发因素和历史过程的综合研究可以实现对滑坡灾害的预测预报[2]。模糊信息检索法在地震预报中应用较多，在滑坡预测预报中的应用还未见报道，根据模糊信息检索法的基本原理和滑坡预测预报的基本要求，笔者尝试将其应用到滑坡预测预报中，取得了较好效果。

1 基本思路

如果某一地区曾经发生多个滑坡，那么这些滑坡不仅包含已发生滑坡的相关信息，而且包含未来该地区滑坡是否发生、将有多大规模等相关信息，这些信息主要包含在滑坡活动性变化指标中，但信息相当模糊，有的可能存在“蛛丝马迹”，有的连“蛛丝马迹”都毫无表征。模糊信息检索法在一定程度上能够辨识这些“蛛丝马迹”，一个模糊信息检索过程就是查问某类滑坡活动性指标与即将发生某种规模的滑坡相匹配的过程[3]。

假设取滑坡活动性指标中的4个指标：某一时间段内发生滑坡次数d1，平均滑坡规模d2，最大滑坡规模d3，大小规模滑坡数目分布特征d4，其中d1、d2、d3可由该地区滑坡历史记录直接得到，d4计算公式为

(1)

式中：nr为第r个时间段内滑坡的总次数；j为滑坡规模类别；njr为第r个时间段内第j类滑坡规模的次数。

d1、d2、d3、d4称为信息描述项，每一个时间段内滑坡的发生情况可用一组各自独立的信息描述项(d1，d2，d3，d4)表示。设有l个时间段要进行检索，则每个时间段可以用1个四维向量来表示：Lr=(dr1,dr2,dr3,dr4) (r=1,2,…,l) ，其中Lr为第r个时间段的滑坡信息特征向量，l个时间段和4个描述项的关系可用一个l×4的矩阵来表示。检索过程中把l个时间段分成若干个类，每类具有相同的信息特征，归好类后，与该类相匹配的滑坡规模即为预报时间段内可能发生的滑坡规模。

2 应用实例

为对模糊信息检索法在滑坡预报中的应用进行检验，选取甘肃省武都县1980年以来的滑坡资料(截至1994年)，统计指标为滑坡次数d1、平均滑坡规模d2、最大滑坡规模d3、大小规模滑坡数目分布特征d4，并以1 年为一个时间段。为保证统计效果，规定只取规模大于1万m3的滑坡进行统计，即所预报的滑坡规模下限为1万m3。武都县滑坡信息统计结果见表1。

将分类标准ML定为10万、50万、100万m3，按每年最大滑坡规模划分为4类：G1为滑坡规模≤10万m3类，对应滑坡分类标准中的小型滑坡；G2为滑坡规模10万～50万m3类， 对应滑坡分类标准中的中型滑坡；G3为滑坡规模50万～100万m3类，对应滑坡分类标准中的大型滑坡；G4为滑坡规模>100万m3类，对应滑坡分类标准中的特大型滑坡。为方便信息检索，将滑坡信息的描述项进行分区，分区结果见表2。

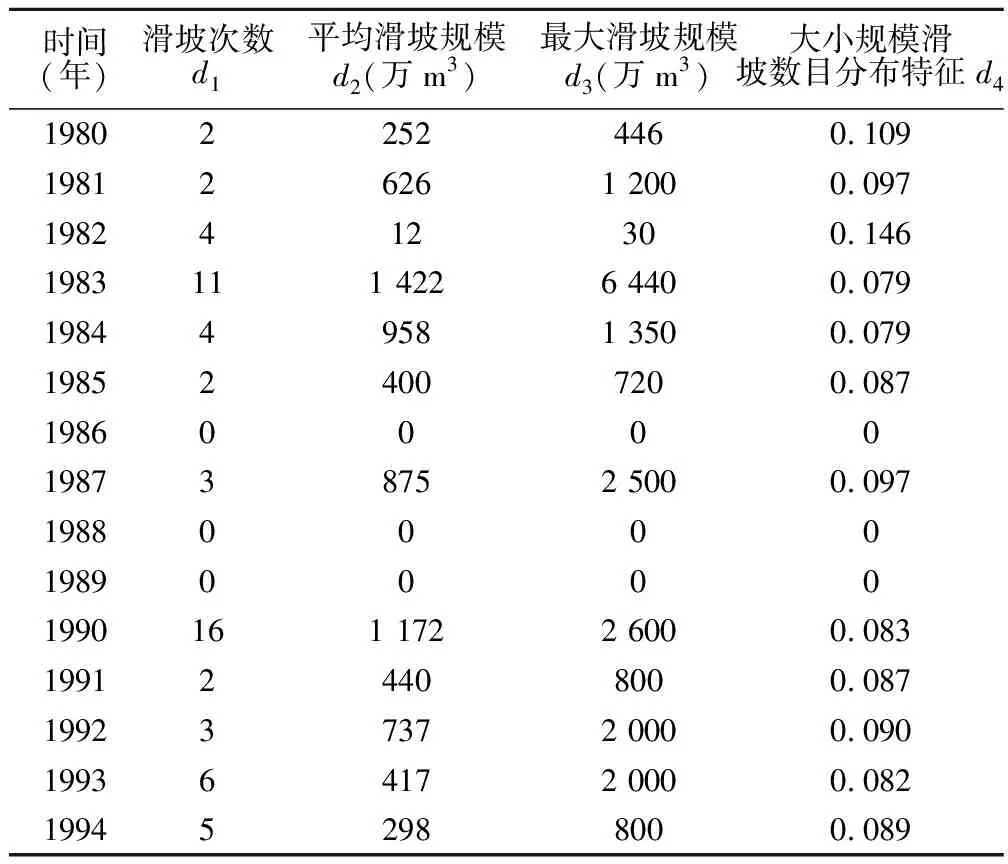
表1 武都县滑坡信息统计

表2 滑坡描述项分区

2.1 滑坡信息项优势概率

由于每个指标的单位、变化幅度、平均值不同，因此必须进行标准化。采用max-min方法，综合4个指标，每个指标对滑坡发生的灵敏度不同，但是对于在特定时间段内某规模滑坡发生时，指标值极大，而无此类滑坡发生时指标值极小，并且每个时段总有某个指标值最大，据此可以求出优势概率M1[3]为

(2)

2.2 各类滑坡发生概率

根据统计方法，在第i个时间段(记为Δxi)内发生第j类规模滑坡的概率可由下式计算[4-6]：

(3)

式中：mj为全部统计资料中第j类滑坡发生的次数；nj为全部统计资料中除第j类外其余各类滑坡发生的次数；mij为Δxi区间内第j类滑坡发生次数；nij为Δxi区间除第j类外其余各类滑坡发生次数。

由概率加法定理可知，用各基本指标项预报第r个时间段内发生第j类滑坡事件的概率[7]为

(4)

Δx1，Δx2，…，Δxl从属于Gj(j=1,2，3，4)的程度用矩阵M2表示[5-7]，列对应于类，行对应于时间段，且按最大类输出，据此可以计算出

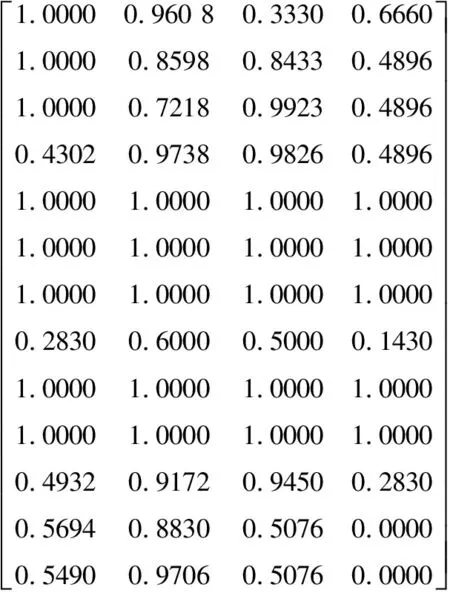
(5)

2.3 某一类滑坡发生的模糊概率

每一时间段总有某一类的滑坡概率为最大，确定的模糊集Gj(j=1,2,3,4)是一个凸集，根据模糊理论，两类滑坡的交集Gi∧Gj也是凸集，可由矩阵M3表示[6-7]，即

(6)

式中：μij(xr)=min(μi(xr),μj(xr))，其中i=1，2,3，4；j=1，2,3，4。

根据矩阵M3，确定一个阈值α≤ min[maxμij(xr)](i=1,2,3,4；j=1,2,3,4)，当某个时段的某种规模滑坡的从属函数μij(xr)≥α时，就可以预报该时段有Gj类滑坡发生。

G12G13G14G23G24G34

(7)

由此得出：maxμ12=0.960 8，maxμ13=0.992 3，maxμ14=0.666 0，maxμ23=0.973 8，maxμ24=0.666 0，maxμ34=0.489 6(其中数值为1.000 0表示从属函数的值为1.000 0，表示已经知晓完全信息，不存在模糊概念，不参与计算)。

α应不大于这六者中的最小值0.489 6，故取α=0.489 6，由此可把15个时间段分成5种不同的时间段，即α值的5个分布区间[0.498 6，0.666 0]、(0.666 0，0.960 8]、(0.960 8，0.973 8]、(0.973 8，0.992 3]、(0.992 3，1.000 0]，表示该时间段内发生某种特定类别Gj滑坡的模糊概率。由于实际情况是要么发生了该类滑坡、要么没有发生该类滑坡，因此在分析中当某一时间段有两种以上的情况可能发生时，按先大规模滑坡、后小规模滑坡、再无滑坡的次序抉择，据此可以对武都县滑坡进行预报，见表3。

表3 武都县滑坡预报结果

根据各年份滑坡规模核定其报准率。从表3可以看出，模糊信息检索法可以用来预报某一地区某一规模滑坡是否可能发生且具有一定的可信度，这种方法也可用来进行多种滑坡前兆观测数据分析。关于选取哪几个预报指标(信息描述项)、用滑坡前多少个时间段的数据进行预报及信息描述项分区界限的设定等细节问题，可以根据具体预报对象及预报经验等灵活处理[4]。

3 结 语

利用模糊信息检索法可以预报滑坡发生规模，本研究中报准率最低为66.7%，最高为100%，平均达到81.7%，同时滑坡次数越多的时间段报准率越高，总体来看在一定范围内可以取得可信结果。但是模糊信息检索法在滑坡预报应用中还存在一些需要注意的地方，比如该方法虽然计算较简单，但计算过程繁琐、信息量大，需要进一步开发程序、编制软件，以方便计算；在滑坡规模突变的情况下，该方法报准率较低，此时可结合其他参数进行综合预报，或扩充样本空间重新计算，以求预报更准确。

[参考文献]

[1] 张建桃,许建瑞.基于GIS的滑坡信息管理和预测预报系统的设计[J].科技情报开发与经济,2005,15(12):226-227.

[2] 方世跃.滑坡预测预报研究[D].兰州:兰州大学，2007：31-35.

[3] 郭新平.乌鲁木齐地区地震活动的模糊信息检索[J].内陆地震,1989,3(4):42-48.

[4] 石耀霖.地震概率预报效能评分和预报发布决策[J].中国地震研究,1992,8(2):23-28.

[5] 冯德益,聂永安,蒋淳.一至数年内地震活动区最大地震震级的统计—— 模糊综合估计[J].地震,1991(6):1-5.

[6] 冯德益,蒋淳,David V J.模糊-统计分析方法在新西兰地震危险性估计中的应用[J].华南地震,2000,20(1):1-5.

[7] 冯德益,顾瑾平,罗瑞铭.地震活动的统计指标与发震时间的概率预报[J].地震研究,1981,4(1):1-6.