超临界雷诺数下拉索顺风向自激力特性研究

祝志文

(湖南大学土木工程学院， 湖南 长沙 410082)

引 言

目前斜拉桥的主跨跨度已达千米量级，随着斜拉桥跨度的不断增大，斜拉索数量越来越多，长度也越来越大。由此导致作用在斜拉索上的气动力也越来越大，甚至可能超过作用在主梁上的气动力。现有斜拉桥颤振稳定性分析，基本上局限在主梁自激力的模拟[1]，不考虑斜拉索可能的自激力作用，而在桥梁颤振临界风速附近的高风速条件下，是否需要补充因拉索振动而产生的气动力，以合理评价拉索气动力和自激作用对超大跨度斜拉桥颤振稳定性的影响，目前并不清楚。

颤振导数的获得，通常是借助风洞试验或计算流体动力学数值模拟。由于拉索外形为圆柱形，其绕流流态和气动力特性对流动雷诺数的变化非常敏感，比如一般认为雷诺数在1.2×105～4×105为圆柱的临界雷诺数区，在该区域，随着雷诺数的增大，阻力系数快速减小[2]，而在雷诺数高于4×105的超临界区，阻力系数又随雷诺数的增大而逐渐增大。因此，颤振导数的识别必须保证拉索流动雷诺数的基本一致性。

在颤振临界风速附近，拉索的流动雷诺数一般在5×105以上，由于拉索一般以低阶频率振动，且超长拉索的基频一般非常低，比如苏通大桥主跨所有拉索的基频均小于1 Hz[3]。对实桥拉索在高风速下的振动，其振动对应的折算风速将非常高，可能超过无量纲值1 000。另外，在高风速下，作用在拉索上的平均气动力可能显著大于自激气动力，加之风洞试验模型惯性力的影响，这样，对高风速下拉索颤振导数的识别，因需同时满足雷诺数和折算风速的一致，这无论对自由振动风洞试验还是强迫振动风速试验均提出了极其困难而难于实现的要求。

采用CFD数值模拟颤振导数，一般是根据折算风速的要求，确定计算的来流风速和模型强迫振动频率，通过确定合理的计算参数，可获得作用在振动模型上的气动力，进而确定对应折算风速下的颤振导数[4]。由于模型采用强迫振动且获得的气动力中没有模型运动的惯性力，因而借助CFD的数值方法几乎成为识别超临界雷诺数下拉索颤振导数，以及评价气动自激力特性的唯一途径。本文以国内某大跨度斜拉桥某根拉索为研究对象，通过数值计算包含强迫振动拉索的计算域，研究了拉索顺风向振动对应的大范围折算风速内的拉索自激力特性，并识别与拉索阻尼项有关的颤振导数。

1 拉索颤振导数的准定常解

在超临界雷诺数下斜拉索的振动实际可能为高折算风速振动，其特征是结构运动速度相对来流风速非常小，因而在拉索运动过程中其运动速度所产生的相对攻角变化非常小，因而可采用准定常假设来描述其运动过程中的非定常气动力。

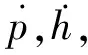
(1)

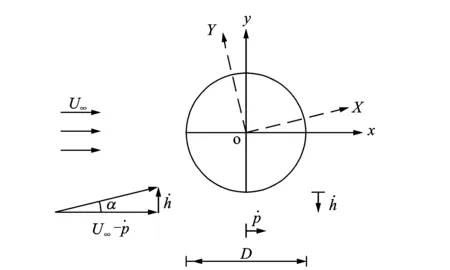
图1 振动拉索上的非定常气动力

上式已假设拉索振动速度远小于来流风速，此时风轴坐标系下作用在拉索上的非定常气动阻力和升力可分别表示为：

(2a)

(2b)

式中ρ为空气密度；CL(t)，CD(t)分别为风轴坐标系下非定常升力和阻力系数，与拉索运动产生的相对攻角有关。在高风速下，拉索振动速度远小于来流风速，设α(t)为拉索合速度与来流风的攻角，因此相对攻角可表示为

(3)

且有sinα(t)≈α(t)；cosα(t)≈1。

如将式(2)转化到以拉索中心为原点的体轴坐标系OXY下，则体轴坐标系下的升力和阻力可表示为：

FV=FDsinα(t)+FLcosα(t)

(4a)

FH=FDcosα(t)-FLsinα(t)

(4b)

如考虑拉索顺风向振动及对应的阻力，且考虑拉索在高风速下的振动为其平衡位置附近的小幅振动，则可将(4b)式在零攻角附近作泰勒展开，考虑圆形截面阻力、升力及其导数特性，并忽略高阶小量，有

(5)

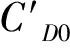
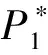
(6)

式中K=ωD/U∞为拉索运动的折算频率；ω=2πf为拉索振动圆频率；f为振动频率。

2 数值方法

2.1 控制方程

绕圆柱形拉索断面的非定常二维不可压流动可用下面的雷诺时均Navier-Stokes方程来描述：

(7)

(8)

上述雷诺应力的引入使得控制方程不封闭，需要引入湍流模型得以求解。如果基于涡粘假设，可将雷诺应力表示为

(9)

式中μt=ρCμk2/ε为湍流粘性;Cμ为经验常数;k和ε分别为湍动能及耗散率，需要通过求解湍流模型方程来确定。由于标准k-ε模型往往过高估计了流动滞点区域的湍动能，一般认为，它不能用于风工程问题的数值模拟[6]。本文采用综合了标准k-ε模型和k-ω湍流模型的SSTk-ω湍流模型。SSTk-ω湍流模型利用了标准k-ε模型适合剪切层模拟而k-ω模型适合近壁区模拟的优点，从而通过设定一个混合函数，使得k-ω模型能在边界层内靠近壁面使用，而边界层外使用k-ε模型求解。相关研究认为，对于分离点附近边界层内的非平衡流动，SSTk-ω能给出明显优于标准k-ε模型的模拟结果[6]。

2.2 计算域和计算参数描述

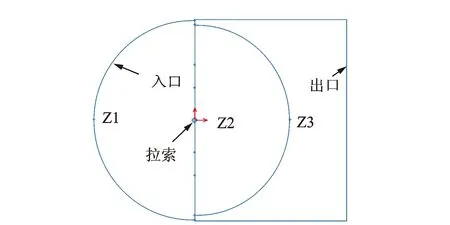
图2 计算域分区

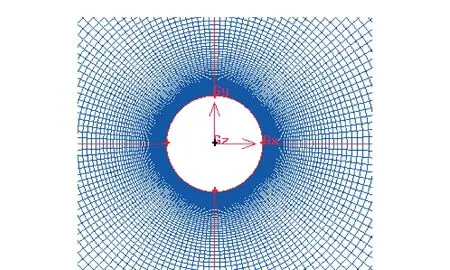
图3 拉索周围的网格

Z1区和Z2区均采用结构化贴体正交四边形网格，Z3区为非结构四边形网格。拉索表面等分为140个网格，为进行网格无关性检查，贴近该表面的第一个网格点到物面的距离h0分别为5×10-6，1×10-5和2×10-5m，分别称之为最细网格G1、细网格G2和粗网格G3。沿物面外法向，3套网格均采用1.06的网格生长率(文献[6]建议的网格增长率不大于1.15)，以保证在物面附近流动变量变化梯度大的位置获得高的网格分辨率。Z2和Z3区的公共边两侧网格尺度也保持平缓变化。对3套网格系统，Z3区的网格划分完全相同，不同的只是Z1和Z2区的网格数量和网格分辨率。这样处理，在拉索周围和尾迹区的大范围内能获得高质量的正交网格。3套网格系统各自的总单元数N见表1。

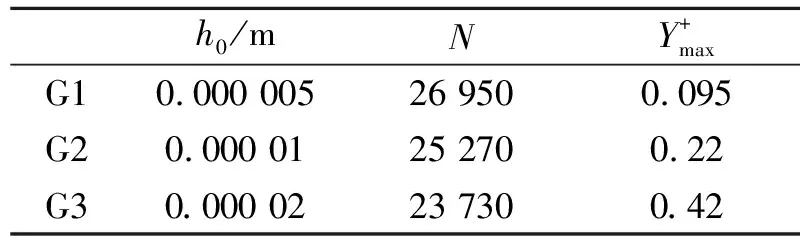
表1 网格划分参数

对计算域外边界，入口处采用自由流速度条件，水平向速度等于来流速度，垂直水平向的速度等于零，来流湍流度取为0.25%。在计算域出口采用流动出口条件，即在出口边界上沿垂直于该边界的法线方向，速度梯度等于零。计算域的上、下边界均采用对称边界条件，即垂直于该边界的速度为零，其它流动变量以该边界内外分别对称。在拉索表面，采用无滑移边界条件，拉索表面粗糙高度与拉索直径D的比值取3×10-5[2]。

2.3 网格无关检查

对拉索绕流的非定常计算，控制方程的时间离散采用二阶隐式格式，空间离散采用二阶迎风格式。压力方程和动量方程的解耦采用SIMPLEC算法和欠松弛迭代。在网格无关和时间步长无关检查中，来流风速在所有工况中维持为63 m/s，对应一个恒定的拉索绕流流动雷诺数5.18×105。为了有效地捕捉流动的非定常特性，非定常计算的时间步长一般要求为圆柱绕流漩涡脱落周期的1/300～1/500[7]，为此，本文通过试算大致确定了漩涡脱落周期，并设定在所有计算工况下的时间步长均为0.000 02。对每一类时间步的数值计算，每一子步进行50次迭代，当动量方程和湍流方程的残差小于10-5时，认为这一时间步的迭代计算已经收敛。气动力系数和其它参数的获取，是在足够多的时间步进数值计算，充分剔除初始计算影响，即气动力系数时程和趋势基本稳定后开始记录的。

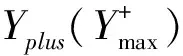
定义拉索截面的非定常阻力系数CD、升力系数CL和扭矩系数CM分别为：

(10)

式中FD，FL和M分别对应作用在拉索截面上的阻力、升力和扭矩，其中阻力顺来流流向、升力垂直来流方向向上、扭矩以拉索顺时针转动为正。

图4中0.3 s以前的时程是固定拉索采用G1网格系统计算得到的气动力系数时程。因受初始计算的影响，要经过0.1 s大概5 000个时间步计算，气动力时程数据才表现为有规律的周期数据。升力系数的主频率为阻力系数的二分之一，也即对应拉索的漩涡脱落频率。为保证固定拉索气动力系数完全摆脱初始计算的影响，本文对上述3套网格系统的绕流计算，均模拟了0.3 s计15 000个时间步。由上述3套网格系统计算得到的阻力和升力系数平均值和均方根值见图5，这些值是根据0.1～0.3 s的时程数据统计得到。

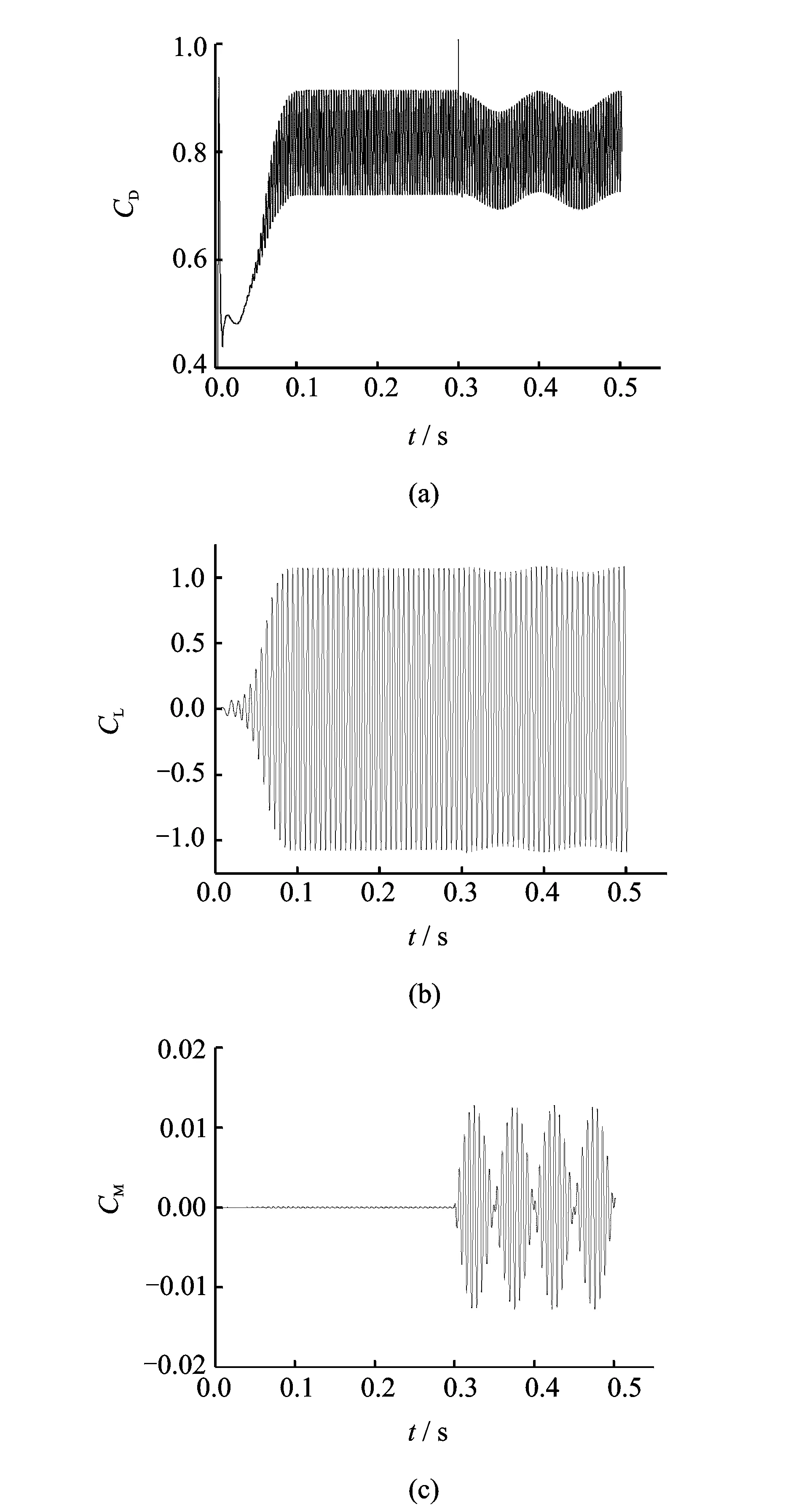
图4 拉索气动力系数时程

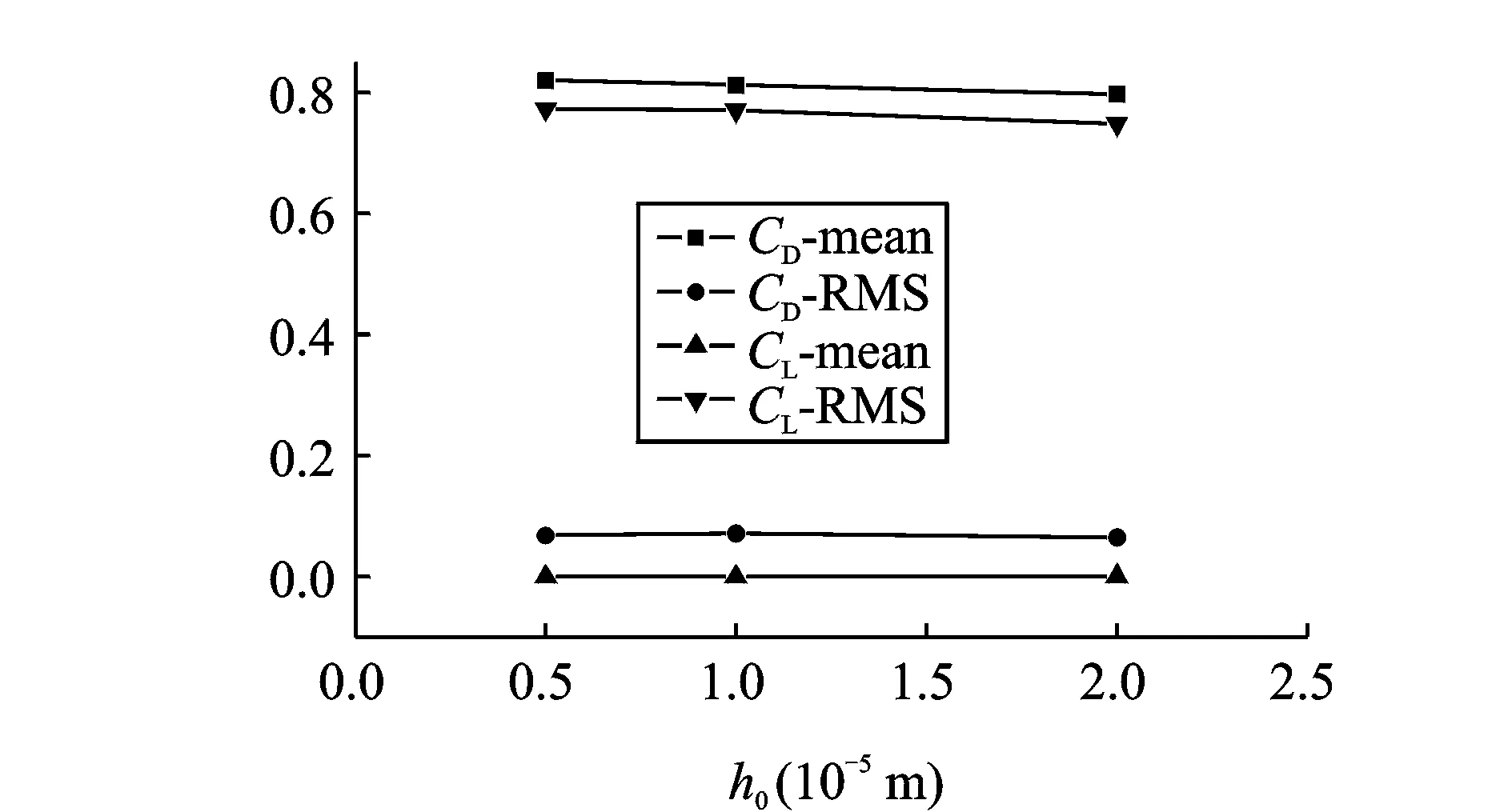
图5 拉索阻力和升力系数平均值和均方根值

从图5可见，固定拉索的升力系数平均值非常小，这是因为拉索外形上下对称(其流态上下并不对称)，其RMS值显著大于其平均值。与此相反，阻力系数的平均值显著大于其RMS值。对3套网格系统，随着物面网格尺度的减小，气动力系数值有稍微的变化，表现为阻力系数平均值和升力系数RMS值有少量的增大，但从G2到G1网格的变化不到1%。阻力系数RMS和升力系数平均值在3套网格系统上基本没有变化。因此可以认为，从网格系统G2到G1，数值模拟结果没有明显的变化，可认为已获得了与网格无关的解。因从网格系统G2到G1，网格数量没有显著增加，因此，在后续运动拉索数值模拟中，本文均采用网格系统G1开展研究。另外，由G1网格系统得到的阻力系数平均值为CD=0.81，可作为准定常理论需要的阻力系数值，这与超临界雷诺数下拉索阻力系数建议值0.8基本吻合[2]，表明了数值方法的有效性，因而可将G1网格和所用计算参数来开展后续拉索自激力特性研究。

3 结果和分析

为获得拉索在来流中运动时，作用在拉索上的气动力，CFD模拟采用单自由度强迫振动法，即强迫拉索作顺风向单自由度、单频率谐振动，拉索强迫运动位移按下式给定

将甘薯淀粉（SPS，sweet potato starch）与魔芋胶（KGM，konjac gum）按以下比例混合（质量比10：0，9.5：0.5，9.0：1.0，8.5：1.5，8.0：2.0），准确称取各配比下的甘薯淀粉、魔芋胶于烧杯中加入去离子水充分混合，配制成质量分数为8%的均一悬浮液（以干基计），于沸水浴中搅拌、加热糊化15 min。除糊化特性外，老化特性、流变学特性的测定均采用该方法制备样品。

p(t)=p0sinωt

(11)

式中p0为顺风向振动位移幅值，通常幅值越大，自激气动力也增大，但如振动幅值很大时，颤振导数识别假定的线性小扰动前提将不满足，可能会出现较大的流动非线性；另外，在CFD模拟中，因在每一个时间步后要重新划分网格，因此振动幅度越大，计算网格的变形幅度也越大，网格的畸变程度越高，这会影响CFD的计算精度。考虑来流风速较大，为增大低振动频率下自激气动力对拉索涡脱力的比值，并权衡模型运动导致的气动力非线性，本文取p0=0.1D，并在Fluent中确认了该振动幅值下网格的畸变不大。

折算风速定义为Vr=U∞/(fD)。因此拉索不同折算风速下的流动模拟仅需通过改变强迫拉索振动的频率，从而得到不同的折算风速[8]。由于来流风速和拉索尺寸不变，因此不同的折算风速模拟仍然保持了相同计算雷诺数，从而使得所有的数值计算条件，如网格、时间步长等参数，在不同折算风速下的模拟保持一致，保证了通过网格无关检验确定的参数能在所有折算风速下完全一致性。

对每一个折算风速下的模拟，为使拉索强迫振动模拟不受初始计算的影响，首先对固定拉索均进行0.3 s共计15 000个时间步的数值计算，大量时间步计算使得拉索绕流能形成稳定的漩涡脱落状态，这可从气动力系数的规则振荡看出，这也是所有折算风速模拟的共同初始条件。然后强迫拉索按给定的位移模式作单自由度运动，振动拉索绕流通过Fluent的动网格实现，在每一时间步计算完成后更新计算域网格。

图4显示了顺风向振动时作用在拉索上的气动力系数时程，0.3 s后为拉索按10 Hz频率强迫振动的2个周期计算结果，对应时间步长的采样频率为50 kHz。从固定拉索状态启动强迫运动，CFD求解在0.3 s后几个时间步上有较剧烈的数值振荡，这主要表现在阻力系数时程上有突跃，这是模型突然运动，导致速度导数不连续导致。随后该现象消失，气动力呈现有规律振荡，表现为拉索涡脱气动力信号受到低频强迫振动信号的调质，且强迫振动的频率越低，气动力的调幅幅度越小，而振动前后阻力和升力系数时程的幅值变化并不大。从涡脱力和自激气动力的幅值来看，阻力和升力系数的涡脱力明显大于自激力，即涡脱阻力和升力主导气动力；从扭矩系数来看，因固定拉索绕流的扭矩系数非常小，因而强迫振动显著增大了拉索的扭矩系数。从振动拉索气动力信号的频域特征分析来看，拉索振动并没有改变拉索绕流自身的漩涡脱落频率。

为了获得拉索强迫振动的自激气动力，需要将总气动力中的涡脱力剔除出来，本文假设小幅振动下气动力满足可叠加性。由于自激力频率明显低于涡脱力，因而可采用低通滤波的方法，将高频涡脱力过滤掉。图6是图5振动拉索在0.3～0.4 Hz的一个完整振动周期内的总气动三分力，以及采用截止频率为15 Hz的低通滤波器过滤后的气动力，对应的折算风速为53。因为过滤所得信号的频率仍为10 Hz，因此本文将其视为由强迫拉索振动产生的自激气动力。从图6的3个气动力系数时程幅值，可见气动力耦合仍然存在。另与总气动力值相比，自激气动力均非常小，但相比而言，沿拉索运动方向的自激阻力系数幅值最大，因而自激力效应将主要体现在与运动一致的自由度方向。

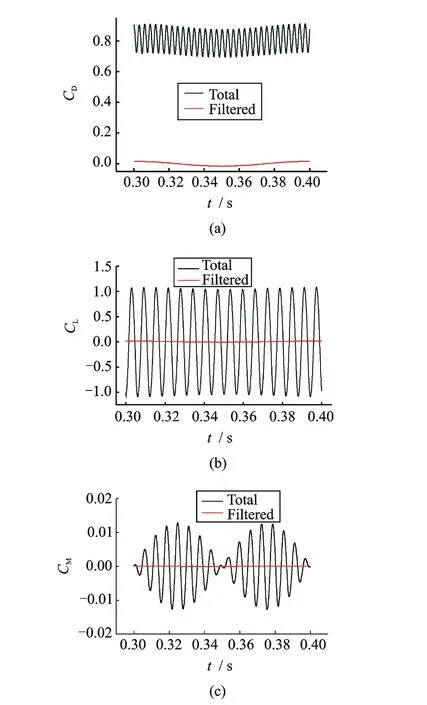
图6 强迫振动总气动力与自激气动力系数时程(Vr=53)

图7是强迫振动频率为0.5 Hz，拉索在0.3～2.3 s的一个完整振动周期内的总气动三分力，以及采用截止频率为1 Hz的低通滤波器过滤后得到的气动力时程，对应的折算风速为1 050。与上图对比可见，在超高折算风速下，拉索自激气动力变化幅值明显小于低折算风速值，特别是沿运动方向的自激阻力系数，这说明随着折算风速的增大，拉索运动产生的自激气动力在总气动力总的比重将减小，本文计算的折算风速为1 050时自激气动阻力系数最大值与阻力系数平均值的比值β约千分之一，因此非常小，见表2。

因此可以认为，在超临界雷诺数下，拉索自激力显著小于其涡脱力，且由于气动力变化频率特征仍主要表现为涡脱频率特征，因此自激力可忽略，风荷载计算只需考虑涡脱力。

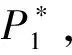
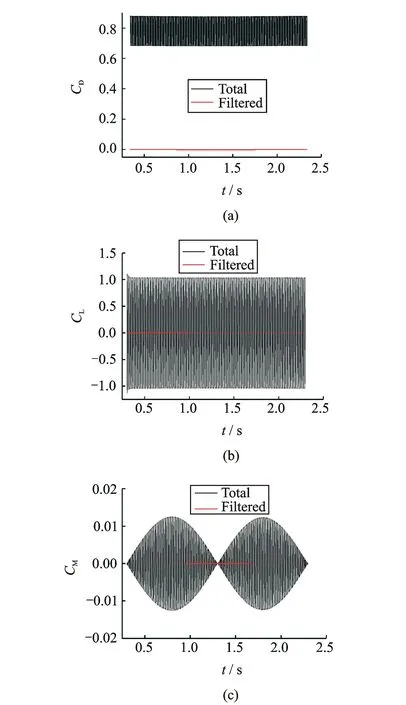
图7 强迫振动总气动力与自激气动力系数时程(Vr=1 050)

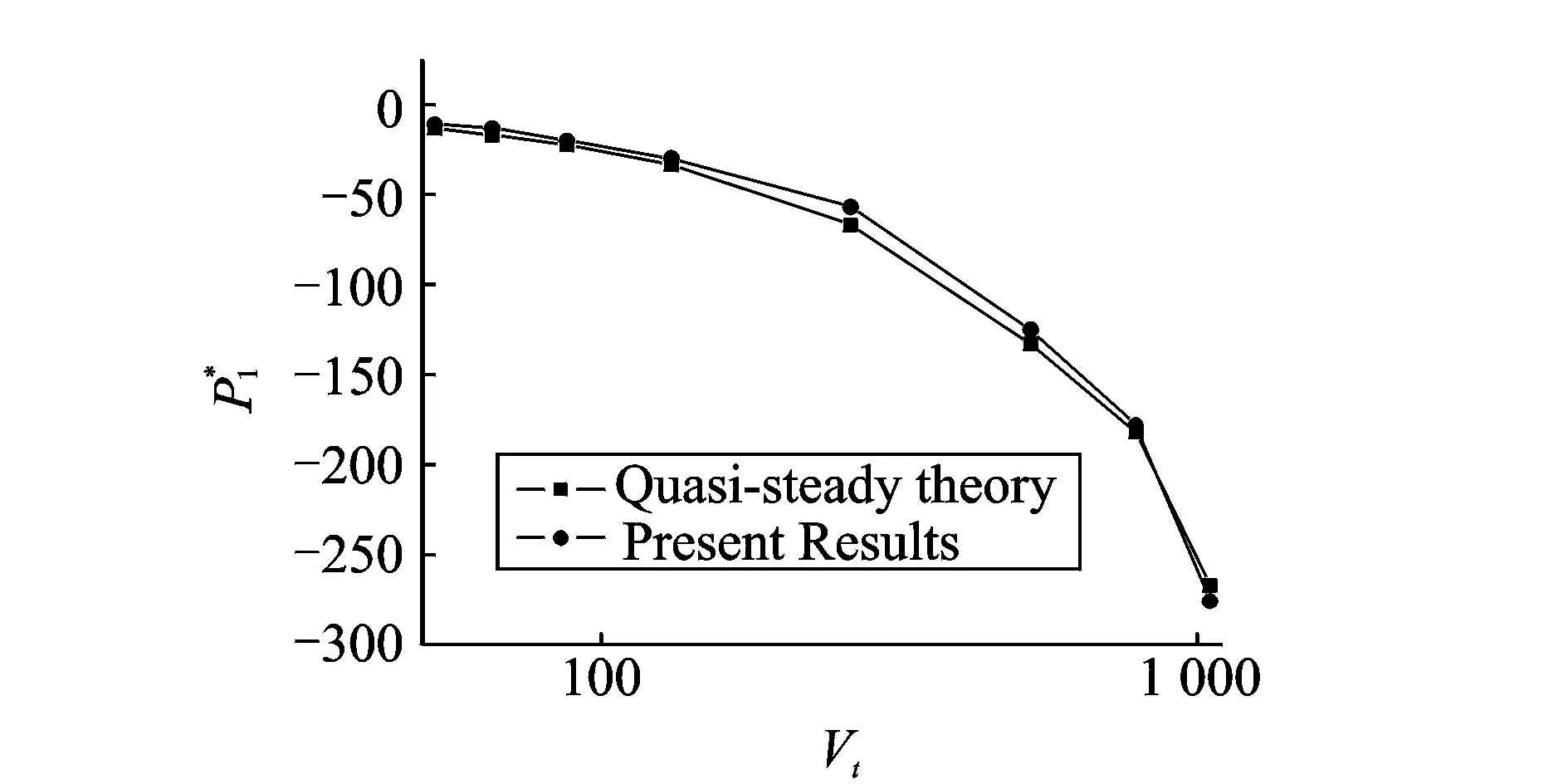
图8 计算的与理论解的对比

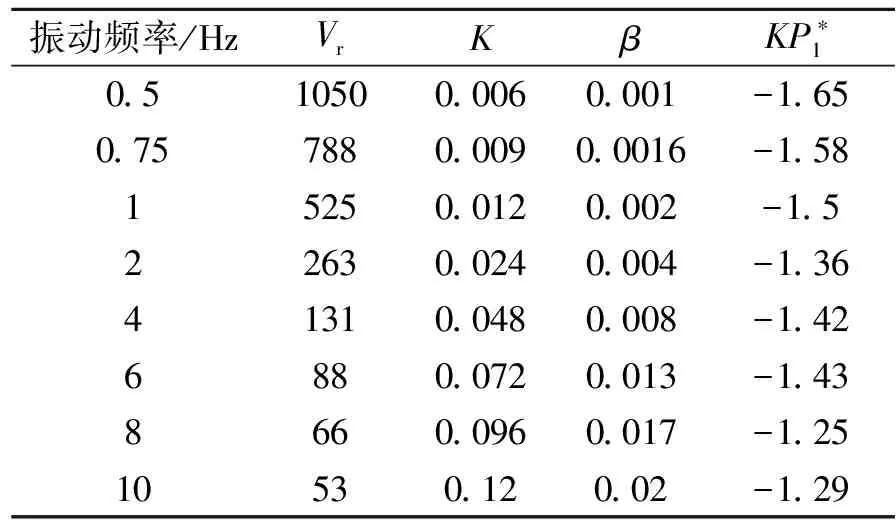
表2 CFD计算工况和相关计算值

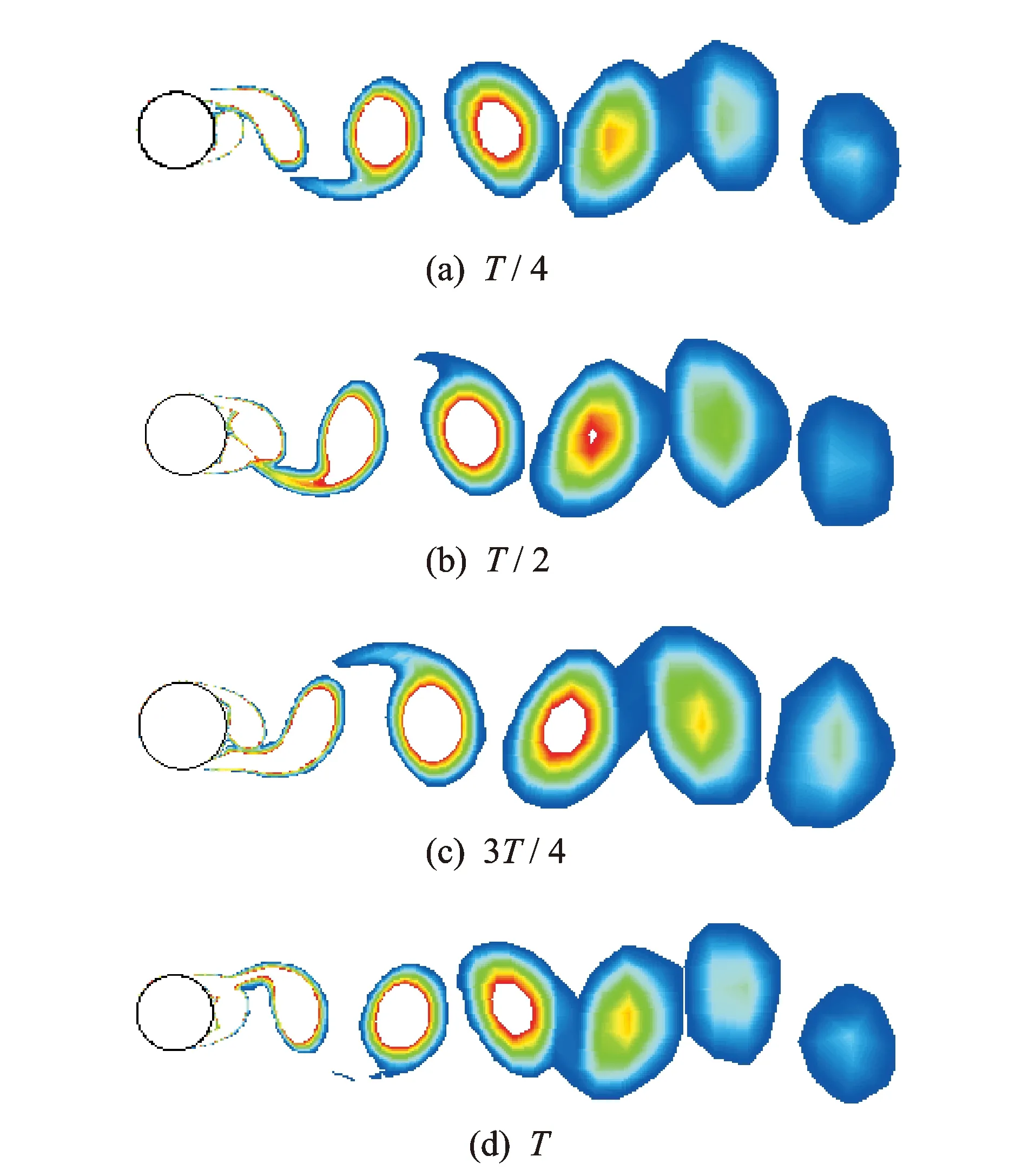
图9 拉索一个强迫振动周期内关键时刻的漩涡脱落图

图9是拉索一个强迫振动周期内的在4个关键时刻的漩涡脱落图，分别对应拉索离开平衡位置到达最大振幅的时刻T/4、回到平衡位置时刻T/2、反向离开平衡位置到达最大振幅的时刻3T/4，以及完成一个周期振动回到平衡位置时刻，其中T为拉索振动周期。虽然可以看到拉索尾迹漩涡的产生、拉长、脱落和随尾迹漂移。

4 结 论

本文基于CFD数值方法研究拉索顺风向振动的自激力特性，得到下述结论：

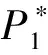
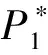
3)在超高折算风速下，拉索自激气动阻力显著小于其阻力平均值，自激升力明显小于升力幅值，即拉索涡脱力显著主导气动力，拉索振动没有改变拉索绕流自身的漩涡脱落频率。

4)在超临界雷诺数和拉索横风向振动情况下，拉索运动产生的自激气动力在总气动力总的比重非常小，对频率特性的改变也非常小，因而自激气动力可忽略，拉索风荷载只需考虑涡脱力。

参考文献：

[1] Ge Y J， Tanaka H. Aerodynamics flutter analysis of cable-supported bridges by multi-mode and full-mode approaches[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000，86：123—153.

[2] Poulin Sanne, Larsen Allan, Drag loading of circular cylinders inclined in the along-wind direction[J]. Journal of Wind Engineering and Industrial Aerodynamics,2007,95:1 350—1 363.

[3] 杨素哲, 陈艾荣, 超长斜拉索的参数振动[J]. 同济大学学报(自然科学版), 2005,33(10):1 303—1 308.Yang Su-zhe , Chen Ai-rong, Parametric oscillation of super long stay cables[J]. Journal of Tongji University(Natural Science), 2005, 33(10): 1 303—1 308.

[4] Zhi-Wen Zhu, Ming Gu, Zheng-qing Chen. Wind tunnel and CFD study on identification of flutter derivatives of a long-span self-anchored suspension bridge[J]. Computer-Aided Civil and Infrastructure Engineering,2007,22:541—554.

[5] Scanlan R H, Tomko J J. Airfoil and bridge deck flutter derivatives [J]. Journal of Engineering Mechanics, ASCE, 1971, 97(6): 1 717—1 737.

[6] Casey M, Wintergerste T. ERCOFTAC Special interest group on “Quality and trust in industrial CFD”, Best practice guidelines[R]. Fluid Dynamics Laboratory, Sulzer Innotec, 2000.1.

[7] Claudio Mannini, Ante Soda, Ralph Voβ, et al. Unsteady RANS simulations of flow around a bridge section[J]. Journal of Wind Engineering and Industrial Aerodynamics,2010，98：742—753.

[8] 祝志文，陈政清. 数值模拟桥梁断面的颤振导数和颤振临界风速[J].中国公路学报，2004，15(4):41—50．Zhiwen Zhu, Zhengqing Chen. Numerical simulations for aerodynamic derivatives and critical flutter velocity of bridge deck[J]. China Journal of Highway and Transport,2004,17(3):41—50.