长周期地震动的特性分析及界定方法研究

李雪红， 王文科， 吴 迪， 徐秀丽， 李枝军， 李晔暄

(南京工业大学土木工程学院， 江苏 南京 211816)

引 言

在现有地震动记录资料中，有两类地震动被认为是特殊的，一类是近断层脉冲型地震动，一类是远场类简谐地震动，研究表明这两类地震动长周期特性明显，因此可称之为长周期地震动[1，2]。随着中国经济的发展，斜拉桥、悬索桥等特大型桥梁及采用减隔震技术的桥梁日益增多，长周期地震动作用下这些柔性桥梁的地震响应日益引起人们的关注[3，4]。张振炫等对比分析了长周期地震动与常规地震动的时、频域特征[5]，表明长周期地震动的低频成分比较丰富，加速度峰值比较小，卓越周期比较长；常规地震动的高频成分丰富，频域分布比较宽，加速度峰值比较大，卓越周期比较短。陈清军等研究表明与常规地震动在各个频率上都有广泛能量分布不同[6]，近场长周期地震动和远场长周期地震动均表现出能量集中在低频处的特征。如何判断和选择长周期地震动，目前的研究成果尚有限，非常有必要对长周期地震动的界定方法进行深入研究。

本文采用希尔伯特-黄变换(Hilbert-Huang Transform，简称HHT)时频域分析方法，分析地震动在不同固有模态函数(Intrinsic Mode Function，IMF)尺度上的能量变化特征，对典型常规地震动和近远场长周期地震动时频域特性和能量特性进行对比，分析长周期地震动与常规地震动的差异；在此基础上，提出常规地震动和长周期地震动的界定参数，通过对大量近远场地震记录的界定参数进行分析，提出长周期地震动的量化评价指标。

1 HHT变换分析方法

经验模态分解(Empirical Mode Decomposition, EMD)方法和与之相应的Hilbert谱统称为希尔伯特-黄变换(即HHT)，它首先采用EMD方法将信号分解为若干个IMF分量之和，然后对每个IMF分量进行Hilbert变换得到瞬时频率和瞬时幅值，从而得到信号的Hilbert谱，Hilbert谱表示了信号完整的时间-频率分布[7,8]。

EMD分解的过程是采用筛分的算法，具体分为三个步骤：第一步找出地震动信号x(t)所有的局部极值点，用三次方样条曲线把全部的局部极大值和局部极小值连接起来，分别画出上包络线xmax(t)与下包络线xmin(t)。第二步求出上包络线与下包络线的平均值，记为m11(t)，将原地震动时程曲线x(t)减去该平均值，则得到新数据序列h11(t)

接着判断h11(t)是否具备有效固有模态函数的两个条件，若不满足的话，则将h11(t)作为原始振动信号按照上述过程继续处理，直到构成的新数据序列

h1k(t)=h1(k-1)(t)-m1k(t)

(3)

具备有效固有模态函数的两个条件，这样就可以得到第1个IMF分量c1(t)

c1(t)=h1k(t)

(4)

从原始信号x(t)中去掉c1(t)，得到剩余的序列r1(t)如下

r1(t)=x(t)-c1(t)

(5)

第三步将r1(t)作为新的信号序列，按照以上的步骤，逐个得出第2，3，…直至得到第n个固有模态函数cn(t)。当EMD分解最后得到的IMF分量rn(t)满足以下两个条件之一，EMD过程就可以结束：(1)残余信号rn(t)的值非常低,低于预先设定好的值；(2)最后的残余信号rn(t)为时间的单调函数。

提取出来的n个固有模态函数蕴含着原始振动信号从高频到低频不同频段的成分，残量则表征了振动信号的振动发展趋势。原信号x(t)则可以表示为各个IMF分量ci(t)与最终残量rn(t)的叠加和，即

(6)

(7)

构造的解析信号zi(t)如下式所示

(8)

进而可以得到振动信号的幅值函数ai(t)为

(9)

对应的相位函数φi(t)为

(10)

于是可以得到瞬时频率

(11)

取实部，这样原信号就转化为

(12)

这里忽略了残量rn(t)，REAL表示取实部。展开式(12)称为Hilbert谱，即H(ω,t)记作

(13)

将H(ω,t)对时间积分，得到Hilbert边际谱，如下式所示

(14)

将H(ω,t)的平方对频率积分，得到瞬时能量谱如下

(15)

2 基于HHT理论的地震动能量特性分析方法

以1999年集集地震中的一条地震动记录为例，对其进行EMD分解，分析该地震动在不同IMF尺度上的变化特征，提出表征地震动能量特性的分析方法。该地震动的11个IMF分量和1个残余函数Res，如图1所示。

从图1可以看出：随着EMD分解的进行，所得各IMF分量(C1～C11)频率逐渐降低，波长逐渐增加。为了能够看出每一个IMF分量的频谱及能量特性，对每一个IMF分量进行HHT变换得到其边际谱与瞬时能量谱。根据式(16)和(17)计算各IMF分量边际谱的中心频率fIMF和平均周期Thm:

式中Bi表示各IMF分量边际谱幅值，fi表示与Bi对应的频率。

为了分析各IMF分量在地震动输入能量中的贡献，根据下式计算各分量的累积能量

(18)

式中IEi(t)表示地震动每个时刻的瞬时能量，E表示累积能量。图2为累积能量谱。进而也可以求得各IMF分量的能量占总能量的比值。

各IMF分量的平均周期及能量比值如表1所示。从表1可以看出各个IMF分量的频率及其对应的能量贡献大小，其中C2分量提供的能量比值最大，其次是C3分量；平均周期随着EMD分解的进行，逐渐增大。

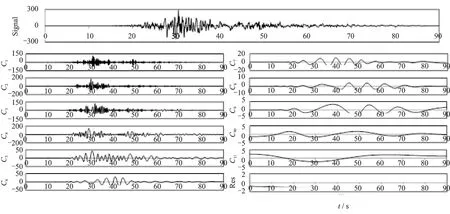
图1 地震动波形图及EMD分解结果

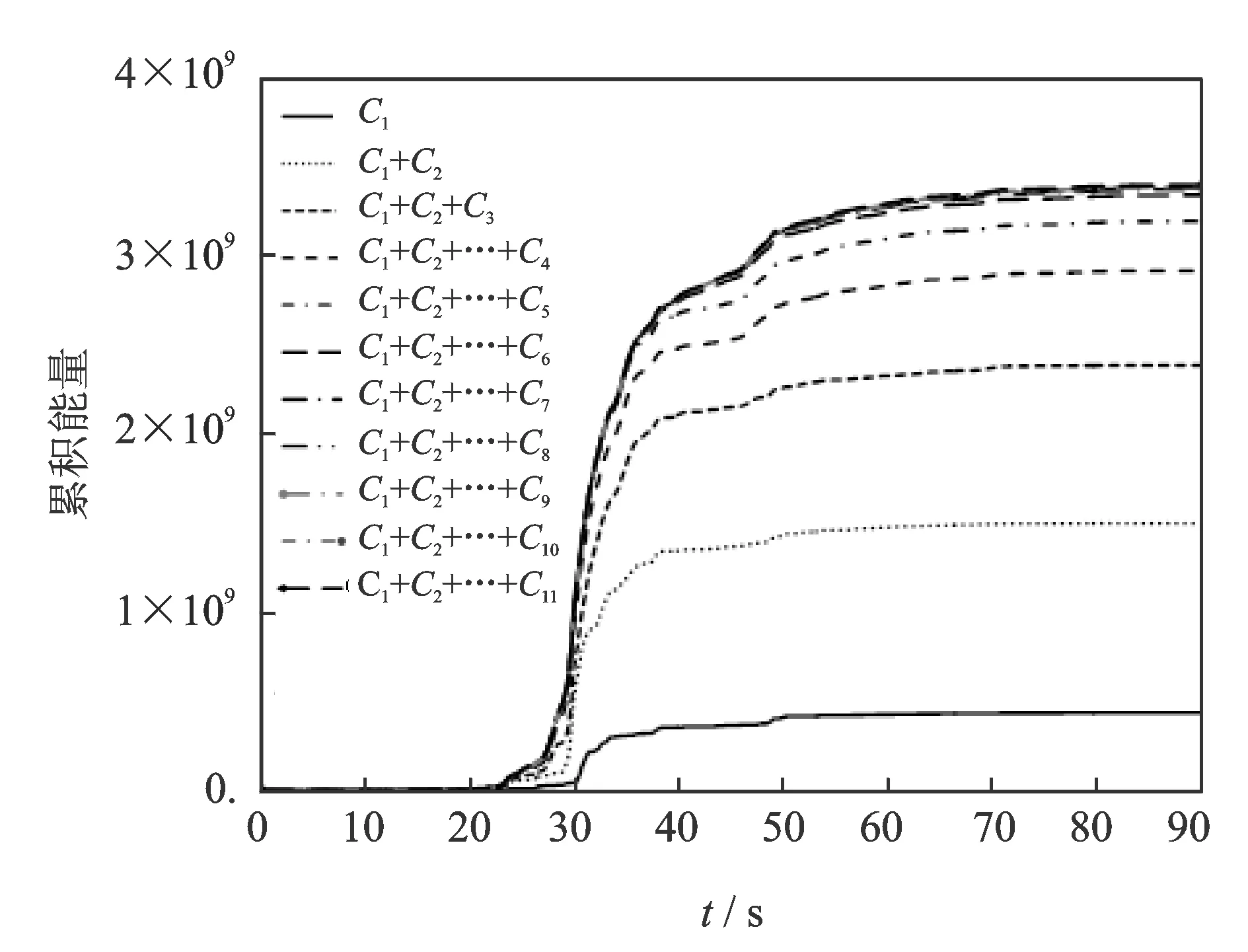
图2 累积能量谱

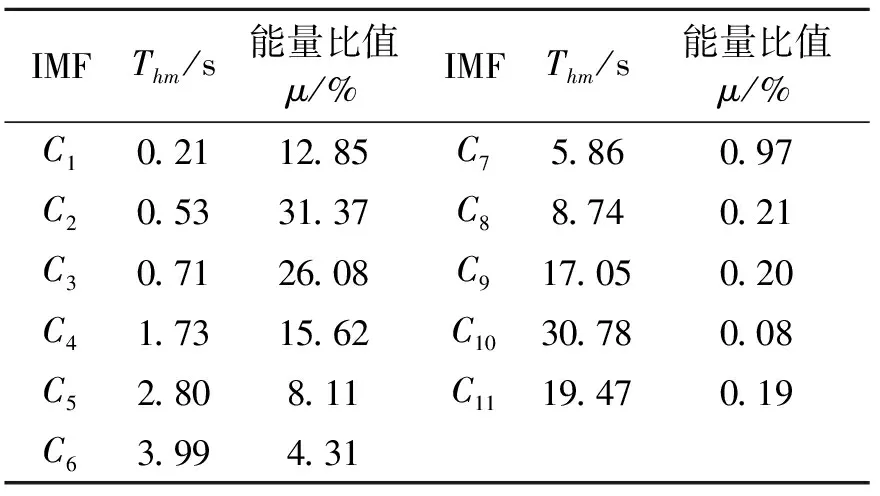
表1 各IMF分量的平均周期及能量比值

有学者提出把能量百分比最大的IMF分量对应的平均周期作为该地震动的主要周期成分，对于本算例，该地震动的主要周期成分为C2分量的平均周期，但是C3分量和C2分量的能量百分比相差不是很大，这样必定忽略了C3分量的周期特性。为了得到主要能量所对应的周期，提出将能量比值累加大于或等于50%的一个或连续多个IMF分量所对应的平均周期按照下式计算其平均值，把能量加权平均周期值Tz作为该地震动主要能量所对应的周期。

(19)

(20)

综上所述，地震动EMD分解后各IMF分量将按频率高低依次排序，各分量的贡献是不同的，利用本文所提出的主要能量对应的平均周期的计算方法分析可知：地震动的Tz越大，地震动的长周期特性越明显；反之，则越弱。

3 地震动的时频特性及能量特性比较

选用6条典型地震动进行时频域特性和能量特性比较，其中2条常规地震动El-Centro波和Taft波、2条典型近场长周期地震动1999年集集地震记录的TCU052波和TCU068波、2条典型远场长周期地震动1999年集集地震记录的ILA004波和2003年十胜冲地震中记录的HKD129波。

3.1 时域特性比较

6条地震动时域信息见表2，加速度时程曲线见图3。PGV/PGA是用来评价一条地震动的脉冲特性，研究表明：PGV/PGA≥0.2表示脉冲特性明显，PGV/PGA<0.2表示脉冲特性不明显[9]。所以从表2和图3可以得出，近场长周期地震动相对持时较短，加速度峰值较大，脉冲特性明显；远场长周期地震动相对持时较长，类简谐波运动较明显， PGV/PGA也大于0.2，由于其幅值较小，并没有近场长周期地震动的脉冲性明显。因此用参数PGV/PGA≥0.2来界定地震动的脉冲特性不尽合理。可通过反映地震动峰值与均值比特征的峰值系数进行评估。

表2 6条地震动的时域信息

3.2 频域特性比较

图4为上述6条地震动从时域到频域的傅里叶谱。由图4可知，常规地震动频率主要分布在1 Hz以上；而近远场长周期地震动频率主要分布在1 Hz以下。

图5为6条地震动的地震动放大系数β谱。由图5可以看出：在大于2 s范围内，近场和远场长周期地震动的β谱曲线差异较小，但近远场长周期地震动与常规地震动差异较大。近远场长周期地震动的β谱下降段比较平缓，而常规地震动的β谱下降较快，这是由于常规地震动和长周期地震动的频谱成分差异引起。

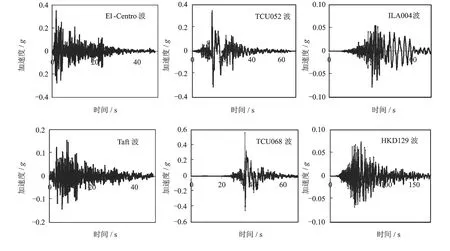
图3 6条地震动的加速度时程曲线

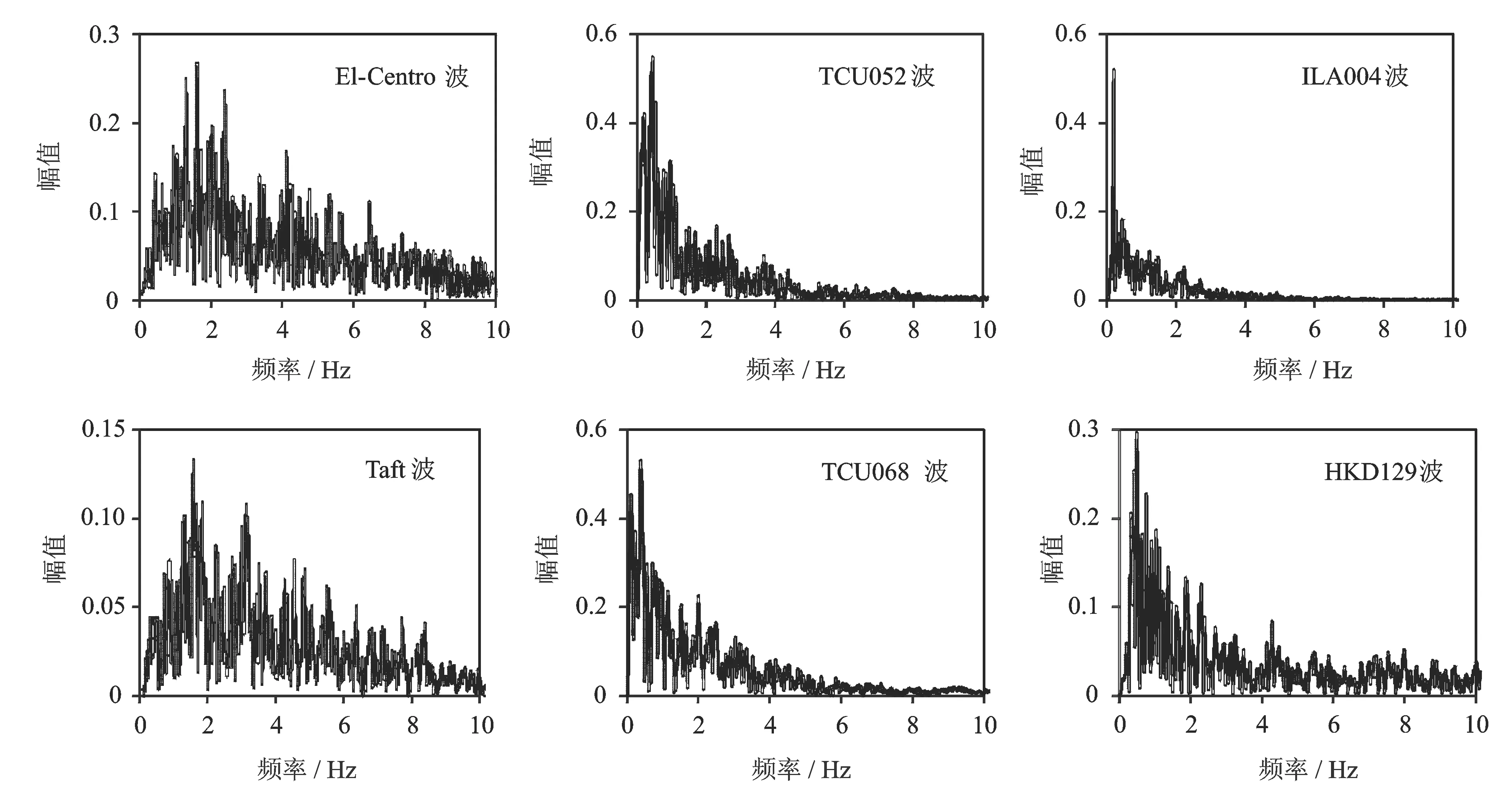
图4 6条地震动的傅里叶谱

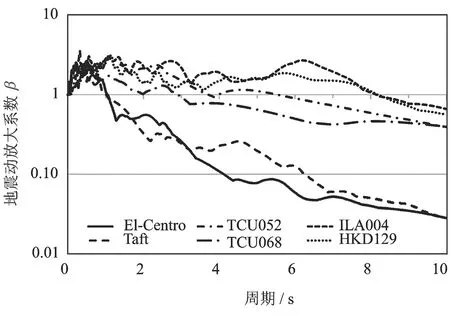
图5 6条地震动的β谱

3.3 能量特性比较

根据本文提出的主要能量所对应平均周期计算方法，计算得到的6条地震动的主要周期，如表3所示。从表3可以看出，常规地震动的主要能量集中在高频部分，而近远场长周期地震动的能量集中在低频部分，且近场长周期地震动的主要周期相对于远场长周期地震动要大，可以看出EMD分解对于长周期脉冲很敏感。

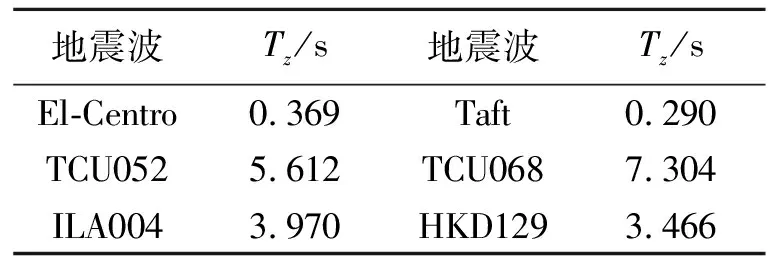
表3 6条地震动的能量加权平均周期Tz值

4 长周期地震动的界定方法

在地震动放大系数β谱上可看到近远场长周期地震动与常规地震动具有明显的差异，长周期地震动β谱在大于2时的谱值相对较高。若一条地震动含有丰富的低频成分，则它对长周期结构的影响是较大的，因此结合地震动特性和结构响应的界定参数才具有一定的工程意义。

为了能够定量地区分常规地震动与长周期地震动，结合二者的β谱的特性，取β谱曲线2到10 s谱值的加权平均值βl如下式所示，为了让计算结果离散性较小，取幅值和离散周期平方的加权平均值。

(21)

式中Ti为阻尼比取5%时加速度反应谱等间距离散周期，Ti的取值范围为[2,10]；Sa(Ti)为Ti对应的加速度谱值；PGA为峰值加速度。

由此定义可以得到6条地震动的βl值如表4所示。由表4可知：常规地震动的βl值较小，近远场长周期地震动的βl值较大，因此可以考虑用βl值作为界定常规地震动与长周期地震动的参数。

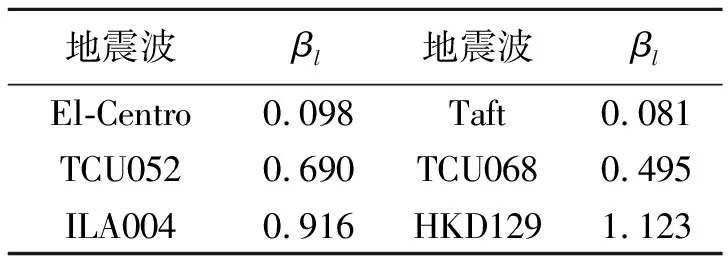
表4 6条地震动的βl值

为了进一步说明用βl作为界定参数的合理性及得到长周期地震动与常规地震动的量化界定标准，本文从太平洋地震研究中心下载了6级以上的地震记录，其中包括1999年集集地震的全部记录。选取传播距离20 km以内的178条地震记录作为近场地震动；选取传播距离100 km以外的151条地震记录作为远场地震动。其中包含不同震级、不同场地、不同峰值的地震动，尤其集集地震包含丰富的近远场长周期地震动[10]，具有一定的代表性。利用Matlab编程得到所有记录的βl值以及频谱分布。为了方便比较，将加速度幅值的峰值都调为1，对傅里叶谱进行了标准化。限于篇幅，图6和7只列出部分典型近场和远场不同βl地震动对应的加速度频谱分布。

为了便于阐述，把地震动傅里叶谱分析中的0～1 Hz频率段称为低频，1～3 Hz频率段称为中高频，3 Hz以上频率段称为高频。所以从图6可得：当近场地震动βl<0.2时，中高频及以上成分较丰富，且主要能量所对应的能量加权平均周期Tz相对较小，类似于El-Centro地震动的频谱分布；当近场地震动βl>0.4时，低频成分较丰富，且主要能量所对应的Tz相对较大，类似于TCU052地震动的频谱分布；当近场地震动0.2≤βl≤0.4时，高频分量较少，但是中高频和低频成分都较丰富，Tz介于上两者之间。图7和6相比，高频成分明显减少，且Tz总体较大，这是由于随着传播距离的增加，地震动高频成分随之衰减。但频率和周期随βl的变化规律与图6相似。所选取的178条近场地震动和151条远场地震动均表现出了类似的规律。因此，基于上述统计分析，可将βl作为界定长周期地震动的量化指标，当地震动βl>0.4时，低频成分比重较大，为长周期地震动；当地震动βl<0.2时，中高频及以上成分比重较大，为短周期地震动(即常规地震动)；当地震动0.2≤βl≤0.4时，为中长周期地震动，介于长周期地震动与常规地震动之间。该指标一方面可以表征地震动对长周期结构的影响，另一方面可以表征地震动的低频成分的比重。

图6 近场不同βl地震动对应的频谱分布

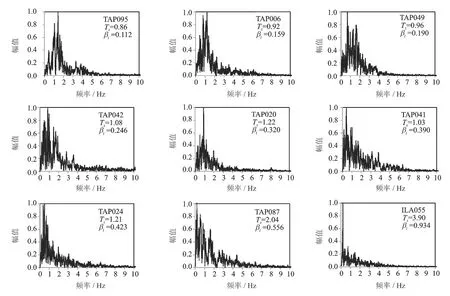
图7 远场不同βl地震动对应的频谱分布图

5 结 论

(1)提出用能量比值累加大于或等于50%的一个或连续多个IMF分量所对应的能量加权平均周期Tz来评价地震动的周期特性，地震动的Tz越大，其长周期特性越明显；反之地震动的Tz越小，则越表现出常规地震动的特性。

(2)近远场长周期地震动的时频域特性和能量特性与常规地震动有明显差异。近场长周期地震动时程曲线表现出强烈的脉冲性，而远场长周期地震动则是类简谐波的特性；而且近远场长周期地震动1 Hz以下的频率成分比重较大，地震动的主要能量集中在低频部分，而常规地震动1 Hz以上的频率成分比重较大，主要能量集中在高频部分；由于频谱分布的差异，长周期地震动的β谱在大于2 s的范围内谱值较大，而常规地震动则较小。

(3)提出用β谱曲线2到10 s谱值和周期的平方加权平均值βl作为长周期地震动界定的指标，随着βl值的增大，高频成分的比重逐渐减少，低频成分的比重逐渐增大，能量加权平均周期Tz逐渐增大；根据178条近场地震动和151条远场地震动的βl值的统计分析结果提出：βl>0.4低频成分占主导地位的地震动为长周期地震动；βl<0.2高频成分占主导地位的地震动为短周期地震动(即常规地震动)；0.2≤βl≤0.4介于两者之间的地震动为中长周期地震动。这将为柔性桥梁抗震分析时长周期地震动的选取和评价提供依据和量化标准。

(4)本文主要针对长周期地震动和常规地震动提出了量化的界定参数；而对于近场长周期地震动和远场长周期地震动的界定后续将进一步研究。参考文献：

[1] Kazuki Koketsu, Hiroe Miyake. A seismological overview of long-period ground motion[J]. Journal of Seismology, 2008, 12: 133—143.

[2] 徐龙军, 胡进军, 谢礼立. 特殊长周期地震动的参数特征研究[J]. 地震工程与工程振动, 2006, 28(6): 20—28.Xu L J, Hu J J, Xie L L. On characteristics of ground motion parameters for special long-period ground motions[J]. Journal of Earthquake Engineering and Engineering Vibration, 2006, 28(6): 20—28.

[3] 臧明明, 陈清军. 长周期地震动的场地效应与大跨桥梁结构的动力响应分析[J]. 结构工程师, 2010, 26(1): 118—125.Zang M M, Cheng Q J. Site Effect of long-period ground motion and dynamic analysis of long-span bridge structures[J]. Structural Engineers， 2010, 26(1): 118—125.

[4] Shoji Gaku. Mechanism of seismic response of a PC cable-stayed bridge subjected to a long-period seismic excitation[J]. Structural Engineering/Earthquake Engineering, 2008,25(2): 982—1001.

[5] 张振炫, 陈清军. 高层建筑结构长周期地震反应的比较研究[J]. 结构工程师, 2009,25(4):78—84.Zhang Z X, CHEN Q J. A comparative study on long-period seismic responses for high-rise structures[J]. Structural Engineers， 2009, 25(4): 78—84.

[6] 陈清军，李英成，胡灿阳．基于正交化HHT法的特殊长周期地震动能量分布研究[J]．力学季刊，2010，31(4)：548—556．CHEN Q J, LI Y C， HU C Y. Study on energy distribution of special long-period ground motion based on orthogonal Hilbert-Huang transform method[J]．Chinese Quarterly of Mechanics，2010，31(4)：548—556．

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society, 1998, A454: 903—997.

[8] 吴琛, 周瑞忠. Hilbert-Huang变换在提取地震信号动力特性中的应用[J]. 地震工程与工程振动, 2006, 26(5): 41—46.Wu C, Zhou R Z. Application of Hilbert-Huang transform in extracting dynamic properties of seismic signals[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 41—46.

[9] Liao W I, Loh C H, Wan S. Earthquake response of RC moment frames subjected to near-fault ground motions[J]. The Structural Design of Tall Buildings, 2001, 10(2): 219—229.

[10] Li Chun-Feng, Zhang Yang, Zhao Jin-Bao, et al. Long-period ground motion characteristic of The 1999 Jiji (Chi-Chi), Taiwan, main-shock and aftershocks[J]. Acta Seismologica Sinica , 2006,19(4): 448—460.