基于动态混淆技术的动态图软件水印方案

，

(郑州大学 信息工程学院，郑州 450001)

网络技术在为人们提供便利的同时，也为侵犯知识产权提供了便利。计算机软件产品开发工作量大、成本高、复制成本低，往往成为版权侵犯的对象。软件水印是近年来出现的软件产品版权保护技术，与软件加密技术不同，软件水印并不阻止对程序的非法拷贝或分发，而是向程序中嵌入一定的版权信息，这些信息可以用来证明版权或追查盗版源。

根据加载的时刻不同，软件水印可以分为静态水印和动态水印[1]。动态软件水印相比静态软件水印鲁棒性较高，是目前研究的热点。本文研究的动态图软件水印由Collberg C等人提出，是近年来研究较多的动态软件水印技术[2]。

动态图软件水印中常用于表示水印信息的图结构有：基数K循环链表、排列图、PPCT图。本文采用可归约排列图(RPG：Reducible Permutation Graph)来表示水印信息。RPG结构中蕴含着唯一的一条哈密顿路径，相比其他图结构，在抵御对动态图水印的语义保持攻击方面有较高的鲁棒性。只靠软件水印一种保护技术，攻击者仍能通过对程序的分析，定位水印的嵌入位置，破坏软件水印。本文将动态图软件水印与代码动态混淆技术相结合，给出了动态混淆的执行过程。利用代码混淆技术对软件进行进一步保护，防止攻击者对程序进行静态分析，从而增加软件水印的抗攻击性。

1 相关理论

1.1 自反排列序列

本文提出的软件水印方案利用RPG结构来表示水印信息。设水印信息用水印数W表示，在采用RPG结构表示水印信息之前，要先把W用自反排列(self-inverting permutation)表示出来。自反排列是一种特殊的排列，它拥有一些特殊的性质，且自反排列图与可归约排列图之间有着一一对应的映射关系[3]。之所以选用自反排列图来编码水印数W，是因为一般情况下，编码自反排列的可归约排列图需要较少的节点，可以提高可归约排列图的数据率。

假设P是序列Nn={1,2,…,n}上的一个排列，K是序列编号，P(K)为排列后所得到的索引号。P-1为P的逆操作，即由索引号推出原来的序列编号。

定义1：如果一个排列{P1,P2,…,Pn}是序列{a1,a2,…,an}上的一个反排列，则其满足Pai=aPi=i。自反排列的反排列是它本身，即PPi=i。

1.2 图的可归约性

设排列图P代表序列Nn={1,2,…,n}上的一个排列，n和d是排列图上的两个节点。

定义2：如果从排列图P的初始节点到节点n的每条路径都要经过节点d,则称节点d支配节点n,记作ddomn。

根据以上定义，每个节点支配其自身，而循环的入口节点则支配循环中所有的节点[4]。可以用支配树表示节点间的支配关系。在支配树中，初始节点是树根，树中每个节点仅支配其后代节点。

对于一个有向图，如果a→b是一条边，其中b称为有向边的头，a称为有向边的尾。在排列图P中，当有向边a→b头支配尾时，称其为一条回边。在回边的基础上，可以定义图中的循环：

(1)循环必须有唯一的入口点，称为首节点。这个入口点支配循环中的所有节点；

(2)至少有一条返回首节点的路径。

给定一条回边n→d，定义该边的自然循环为d加上所有不经过d而能到达n的节点的集合，d是该循环的首节点。可归约排列图中的循环是自然循环，且不存在从循环外到循环内的边。所以，在RPG结构中，边进入循环只能通过循环首节点。

1.3 可归约排列图(RPG)

可归约排列图是一种具有较高鲁棒性的图结构。一个典型的可归约排列图由四部分组成[5]，如图1所示。

(1) 头节点。在每一个RPG图中都有一个头节点，其是RPG图中唯一一个入度为0的节点，其出度为1，RPG中的其他节点都可通过该节点到达；

(2) 序列节点。序列节点紧跟头节点，任何排列节点都可以通过其与序列节点间的边访问到排列节点中的其他任何节点；

(3)排列节点。该节点间的边可编码一个自反序列；

(4)尾节点。其出度为0，并且通过任何一个排列节点均可到达。

图1 RPG图

在RPG图中存在着唯一的一条哈密顿路径，这条哈密顿路径确定了节点的初始编号。在可归约排列图中，从每个排列节点出发有两条有向边，一条边用于形成哈密顿路径，另一条边则对这些节点进行排列图编码。

不同于一般的排列图编码，可归约排列图中排列节点间的边必须保证排列图的可归约性。RPG图中序列节点的作用是保证序列图的可归约性。在生成RPG图时，需要删除排列节点间可能影响到排列图可归约性的边，而对于被删除的边，可以用其关联节点与序列节点对应的边来表示。

1.4 程序动态混淆保护

代码混淆技术[6]是把程序S转换成S′，程序S和程序S′的行为一致，但攻击者很难从S′中获取信息。本文采用动态混淆技术，该过程分为2个阶段：第一个阶段在编译时执行，将程序中需要保护的代码进行初始转换，并在程序中添加运行代码转换器；第二个阶段在程序运行时执行。通过这些变换，动态混淆器把一个普通的程序变成了一个自修改的程序。图2是动态混淆的转换过程。

图2 动态混淆转换过程

2 基于动态混淆的动态图软件水印方案

在水印嵌入时，首先将水印信息用水印数W表示，然后用RPG结构表示该水印信息，并通过CT算法将生产RPG结构的代码嵌入到程序S中。对于嵌入水印的程序S，使用动态混淆技术对其进行加密，防止程序被静态反编译，增加程序的抗攻击性。

2.1 水印图的嵌入

采用RPG图来编码水印信息W。与基数K编码、排列图相比，RPG结构的鲁棒性较高，且RPG图中每个节点的指针数小于等于2，与程序中其他数据结构相似，有较高的隐蔽性。对于代表水印W的RPG结构，采用CT算法将其嵌入到程序S中。CT算法是一种动态软件水印算法，可将水印图G拆分成一系列的子图嵌入程序S中。在将水印数W用RPG结构表示之前，需要先将W用自反排列序列表示。

利用Collberg C提出的算法能产生可归约的排列图。在算法中添加序列节点来保证整个排列图的支配树不变。在可归约排列图中最多含有一条哈密顿路径，且可以用多项式时间算法找到该路径。一旦确定RPG结构中的哈密顿路径，按在该路径中的先后顺序对节点进行编号，确定所表示的排列，即可得到编码的水印信息。对于同构的有向图来说，其对应的哈密顿路径是相同的。即使攻击者通过调整程序中结构体指针的顺序来扰乱水印，软件所有者仍能提取出正确的水印。

2.2 水印信息的提取

在提取水印信息时，水印图会在程序运行时动态地产生于程序的堆中。在当得RPG图后，需要提取嵌入RPG图中的水印数W。假设RPG图G=(V,E)，通过以下算法步骤，可以提取图中蕴含的排列：

(1)计算图G的支配树，确认图G是可归约的；

(2)用Bellman-Ford算法获得G中的哈密顿路径；

(3)取哈密顿路径上的首节点v0为第一个节点，哈密顿路径上的其他节点为v1,v2,…,vk-1，f；如果在头节点h与首节点v0之间还有其他节点，设这些节点为pm,pm-1,…,p1；

(4)取集合B={v0,v1,…,vk-1}；

(5)创建一个节点的空排列L，对于每个i∈{0,1,…,k-1}，如果有一条从vi到节点B∪{f}的边，则将节点vi添加到L中。如果vi没有到集合{pm,pm-1,…,p1}的边，将其插入到序列的尾部;如果vi有边到pj，就把vi插入到序列L的倒数第j个元素之前；

(6)对i∈{0,1,…,k-1}，如果vi有一条从B∪{h,p1}的入边，则添加一条从排列L的首节点到vi的边，然后将L中的首节点从序列中删除；

(7)初始化有K个元素的整数排列A，令A[0]=0。对于i∈{1,2,…,k-1}，经过上面的步骤，节点vA[i-1]→B∪{f}有且只有一条边不属于哈密顿路径。如果某条边指向了节点vi,则A[i]=j;如果某条边指向尾节点f,那么A[i]=a[i-1]+1。最后得到的排列A就是所求的排列。

由于RPG结构中的节点顺序由其中蕴含的哈密顿路径P所确定，而每个RPG结构中最多有一条哈密顿路径，因此该算法将从任何两个同构的图中提取相同的排列。对于改变结构体指针顺序的攻击，RPG结构有着较强的鲁棒性。上面的水印图生成提取算法由Collberg C等提出[5]，可以在多项式时间内完成自反排列到水印图的转化。关于自反排列图如何高效地得到水印数据W，国外学者也进行了相关的研究。Chroni M等人提出了一种有效的转换方法，将水印数W先转化为二进制，可以在O(n)时间内完成水印数据到自反排列的转换[7]，其中n是二进制的位数。

2.3 动态混淆加密防篡改

把程序分成若干个片段，并且不停地把这些片段进行异或运算。如果攻击者想在调试器中分析被保护的程序，会发现程序中只有某些片段处于明文状态。通过这一保护措施，增加了破解者分析程序的难度，增强了软件水印方案的鲁棒性。

设S是动态混淆加密前的程序，首先把程序S分成若干个片段，分别记为CB1,CB2,…，CBn，接着对这些片段进行预处理，经过处理的程序S由若干个片段组成，除第1个片段是明文外，第2个到第n个都是不同代码片段内容之间异或的结果。这样当攻击者分析程序时会发现，程序中大部分代码都经过了加密，破解难度增加。处理后的程序S的结构如图3所示。

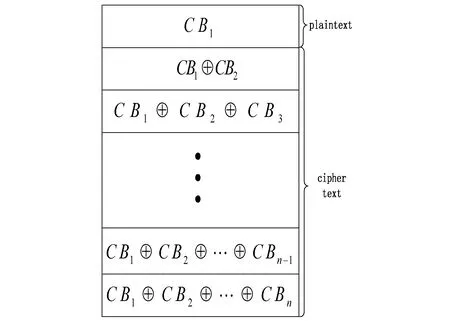
图3 混淆加密后的程序

在执行时，加密处理后的片段分别放在EU(encrypted unit)的结构单元中。EU结构如图4所示：

图4 EU结构图

在图4中，IVi是EU的初始值，其中存放的是经代码混淆后的程序S的代码片段；函数F是个变异函数，相当于一个运行代码转换器，它的作用是把IVi与下一个EU中的代码块IVj进行异或运算；“Jump next”是转向下一个单元执行。

图5所示是一次程序的执行过程。M0，…，Mn表示程序执行过程中的不同状态，其中M0是程序被混淆后的最初状态。在程序执行时，第一个单元是明文的，因为它马上要执行，不能是密文。随着程序的运行，当一个EU中的代码块运行完毕后，变异函数会将本单元中的代码块与下一个将要运行的EU中的代码块异或，解密其中代码块的内容。

图5 动态混淆执行过程

例如程序S执行到M2状态时，程序会执行代码块CB3中的内容，当CB3中代码执行完毕后，将前一个EU单元中代码块的值CB1⊕CB2与本单元中代码块的内容CB3进行异或，然后将EU单元中的代码块还原为执行前的内容，最后变异函数再将还原后的代码块异或到下一个EU单元中的相应位置，将其中的内容解密，解密后通过跳转模块将程序的控制流转移到下一块中。当程序S的每个代码被依次执行一遍之后，将回到初始状态。这样可保证程序S在每次执行时，程序中的代码总是一样的。

3 性能分析

3.1 鲁棒性分析

本文选用RPG图作为嵌入水印的拓扑图。由于RPG图中节点间的排列顺序被编码到了图中唯一的哈密顿路径中，对于同构的排列图，仍然能正确地提取节点间的编号。因此对动态图软件水印的边翻转语义保持的攻击有较高的鲁棒性。RPG图中每个节点的指针数较少，与程序中其他数据结构相似，有较高的隐蔽性，对攻击者的模式匹配攻击也有较强的鲁棒性。

本文采用动态混淆加密技术，给嵌入了软件水印的程序增加了一层额外的保护，使得被保护的程序能抵御攻击者对程序的静态反编译，能有效防止攻击者对程序的非法修改。

3.2 数据率分析

动态图拓扑结构的数据率体现了其能够隐藏信息量的多少，常见的动态图拓扑结构中，基数K编码的数据率最高，PPCT的数据率最低。而RPG图的数据率约为基数K编码的一半，但高于PPCT编码。Collberg C等人给出了可归约排列图编码的数据率下限，节点n的RPG图的数据率至少为(lgn-lge-1)/4[8]。

3.3 自恢复功能

软件水印方案能有效抵御程序的静态反编译，但是，由于程序的起始代码片段总是明文的，而且每个代码片段在执行前总是要恢复成明文，因此，当动态执行程序时，有经验的攻击者可以通过在每个代码片段前设置断点，逐段恢复其中的代码。一旦攻击者获得了程序中的代码，就可以对其进行修改，破坏其中嵌入的图拓扑结构，进而影响水印的提取。本文提出的软件水印方案采用的RPG图不仅有较高的鲁棒性和隐蔽性，还是一种纠错图，能一定程度上抵御对动态图结构的攻击。RPG图的每个节点都有2条引入的边，一条边用于排列编码，一条边用于形成哈密顿路径。如果攻击者修改了RPG图中的一个指针，在提取水印信息时，将导致一个节点的入度小于2，同时错误的边很容易被找出，所以，RPG图能够纠正一条边的错误。同时由于该图中编码的哈密顿路径是唯一的，故当其受到边翻转攻击后，虽然图结构发生了改变，但仍能从同构的图中提取原节点编号，恢复水印信息。

4 结 语

本文提出的软件水印方案将动态图软件水印技术和代码动态混淆技术相结合，将水印信息用RPG图表示，并嵌入到程序中，对嵌入水印的程序用动态混淆技术进行保护，抵御攻击者对程序的静态反编译，提高了软件水印方案的抗攻击性。动态代码混淆技术的引入，虽然可以为软件水印方案提供较高的抗攻击性，但可能会导致程序性能的下降。

参考文献：

[1] 张立和,杨义先,钮心忻，等.软件水印综述[J].软件学报,2003,14(2):267-277.

[2] Collberg C, Thomborson C.Software Watermarking: Models and Dynamic Embeddings[C]//Proceedings of the 26th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages.Texas, American: Springer-Verlag,1999:311-324.

[3] Chroni M, Nikolopoulos S D.Encoding Watermark Numbers as Cographs Using Self-inverting Permutations[C]//Proceedings of the 12th International Conference on Computer Systems and Technologies.Greece :ACM, 2011: 142-148.

[4] Alfred V Aho, Ravi Sethi, Jeffrey D Ullman.编译原理[M].李建中,姜守旭,译.北京:机械工业出版社,2003:392-393.

[5] Collberg C, Kobourov S, Carter E, et al.Error-correcting Graphs for Software Watermarking[C]//Proceedings of 29th Workshop on Graph Theoretic Concepts in Computer Science.Netherlands: Springer, 2003: 156-167.

[6] Collberg C, Thomborson C.A Taxonomy of Obfuscating Transformation[R].New Zealand: University of Auckland, 1997.

[7] Chroni M, Nikolopoulos S D.Efficient Encoding of Watermarking Numbers as Reducible Permutation Graphs[R].Ioannina: University of Ioannina, 2011.

[8] Collberg C, Thomborson C, Townsend G M.Dynamic Graph-Based Software Watermarking[R].Arizona: Unirersity of Arizona, 2004.