一种模型检测精确加速的判断方法

， ，,2，

(1.郑州大学 信息工程学院， 郑州 450001; 2.吉首大学 数学与计算机科学学院，湖南 吉首 416000)

基于时间自动机的模型检测是一种经典的自动验证技术，它具备成熟的理论基础并广泛应用于安全认证协议、控制系统等领域。在实时系统中，由于控制程序和外界环境经常使用不同的时间度量，当以时间自动机为基础，运用符号模型检测技术进行可达性分析与验证时[1]，验证速度会因为状态空间的片段化问题明显下降[2]，导致模型检测时间和空间增加，甚至无法完成检测。

加速技术主要用来解决由于时间度量不同造成的片段问题。文献[3]结果表明加速技术应用在合并扩展中可以提高分析的精确性；文献[4]介绍了利用硬件设备实现模型检测加速的方法；文献[5]利用两个SAT求解器作为验证引擎，对在线模型检测进行了加速；文献[6]和[7]分别向可加速环添加了一个附加环和驻留环，构造了加速自动机模型，从而实现了加速。这些方法在大多数情况下能够有效加速前向符号可达性分析过程，而且不改变时间自动机原有的可达性。

上述加速方法对于时钟带片段数量非常多的系统模型具有很好的加速效果，而对于片段数量较少，或者片段之间的关系不满足一定条件时，加速效果不明显，甚至会降低验证速度。

本文对基于附加环的精确加速技术进行分析，用加速效益和加速代价来衡量附加环的加速效果。通过分析加速过程中的主要参数，推导出了附加环加速能否有效的判断条件。

1 基本知识

1.1 时间自动机

定义1(时间自动机) 假设M=(Loc,l0,X,A,I,E)是一个六元组的时间自动机，其中Loc是有穷控制位置的集合；l0∈Loc是初始位置；X是时钟集；A是有穷动作的集合，包括协同动作和内部动作；Loc→Φ(X)是一个映射，I为每个控制位置分配一个不变式；E⊆Loc×A×Φ(X)×2X×Loc是有穷边的集合。一条边(l,a,φ,λ,l′)表示一个迁移。如果位置l的时钟取值满足时钟约束φ，那么系统可以通过动作a从位置l迁移到另一个位置l′，同时把λ∈X中的所有时钟复位。

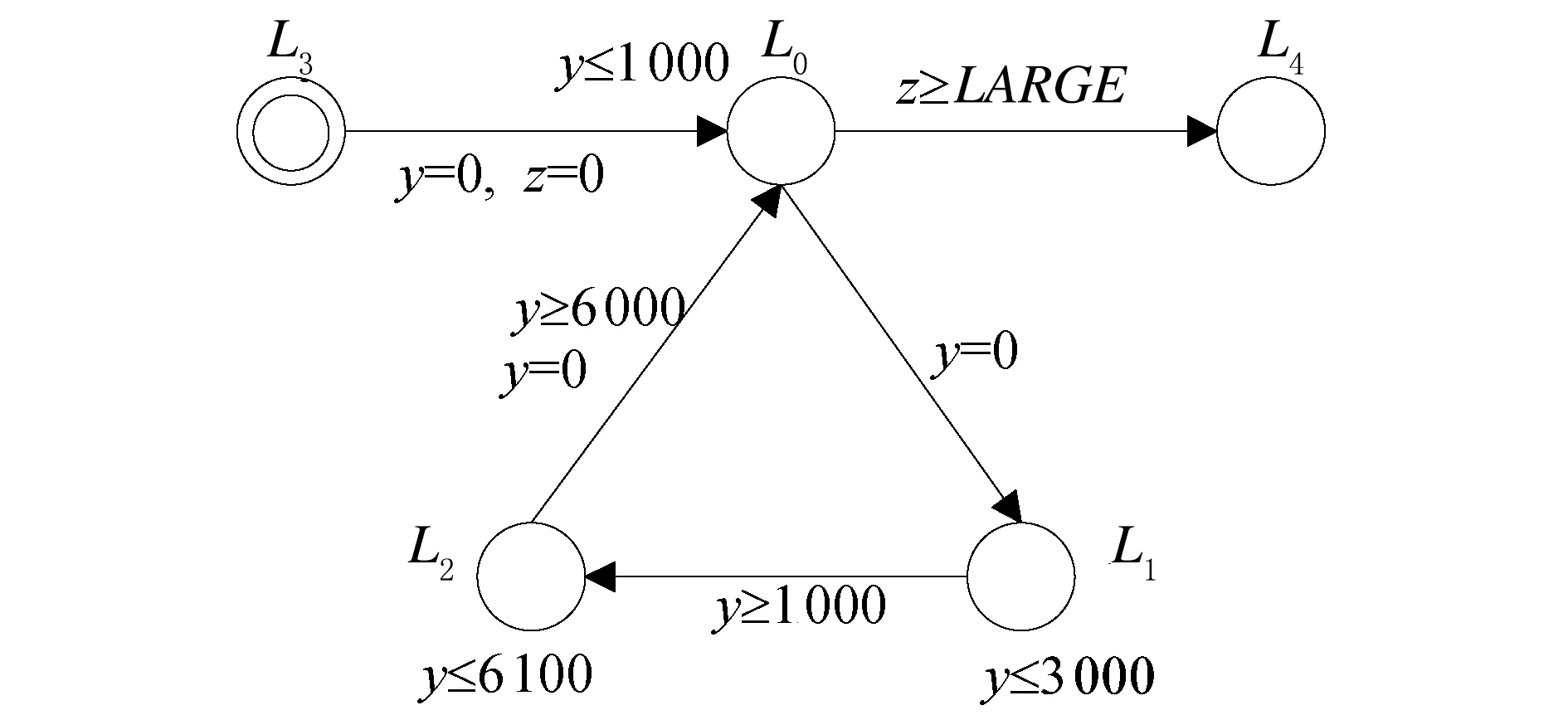
图1是由控制程序和外部环境组成的时间自动机的抽象模型，L3是模型的初始位置。由位置L0、L1、L2组成的控制环对控制程序进行循环执行，z是外界环境时钟。当时间自动机处在控制环的位置L0时，就会检查时钟z是否满足z≥LARGE，从而决定是否跳出控制环而到达位置L4。

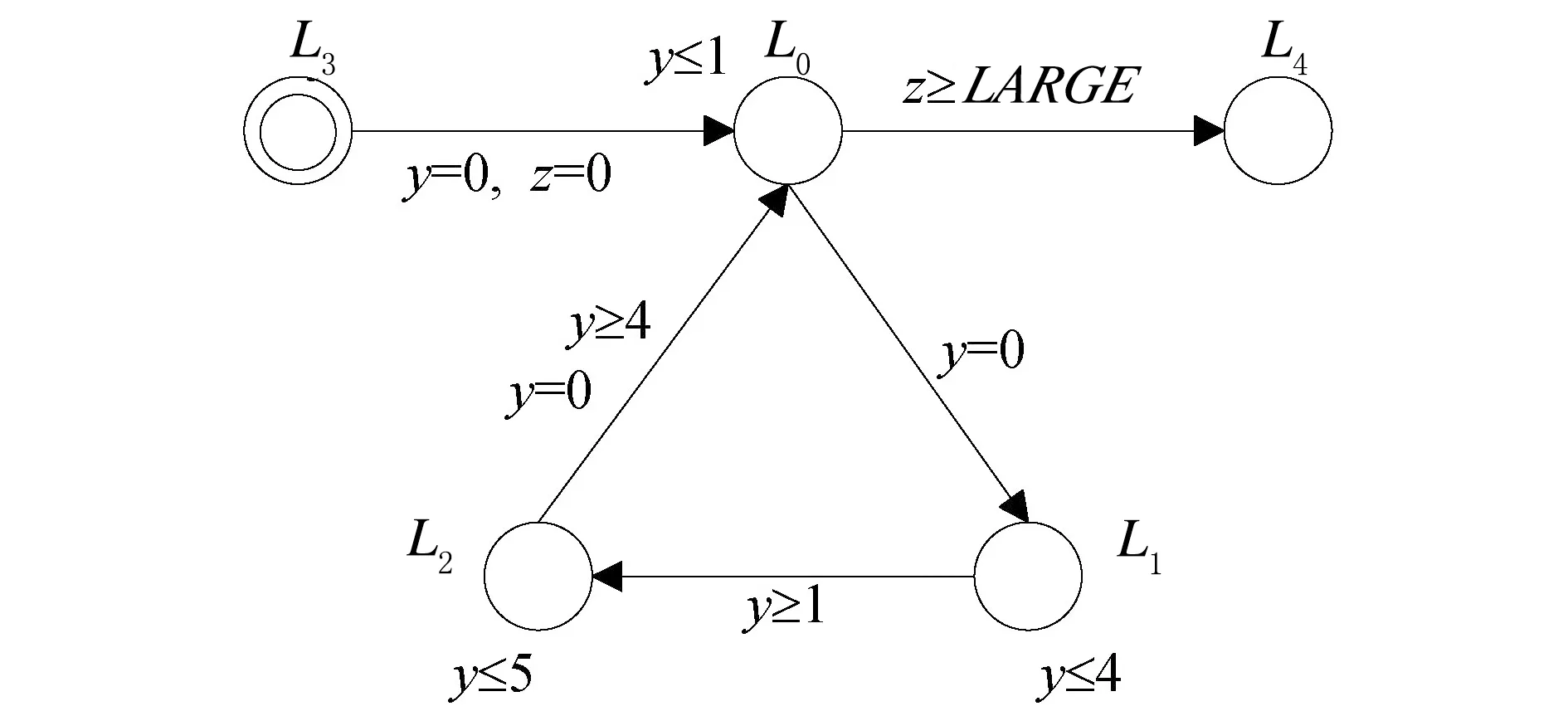
图1 时间自动机P的抽象模型

1.2 前向符号可达性分析及片段问题

实时模型检测工具UPPAAL的模型检测引擎从初始状态开始[8-9]，对可达的符号状态空间进行前向搜索，判断某个给定的状态是否可达。对每个还未被搜索的符号状态，计算出它的后继状态(时延或动作引起的)，并且与已经搜索过的状态进行比较，如果某个后继状态已经出现过，就忽略它。相反，如果一个后继状态没有出现过，就把它保存到待检测状态列表，以便进一步搜索[10]。

为了说明前向符号搜索过程，考虑图1中的时间自动机P,表1给出了从初始状态开始，通过前向符号搜索执行两次控制环得到的符号状态。当搜索到第5个符号状态时，其控制位置与第2个符号状态的控制位置相同，但由于它的时钟带并不包含在第2个符号状态的时钟带中，因此，根据模型检测可达性分析算法，应该对这个状态进一步搜索。同样，对于第8个符号状态也应该进一步搜索。

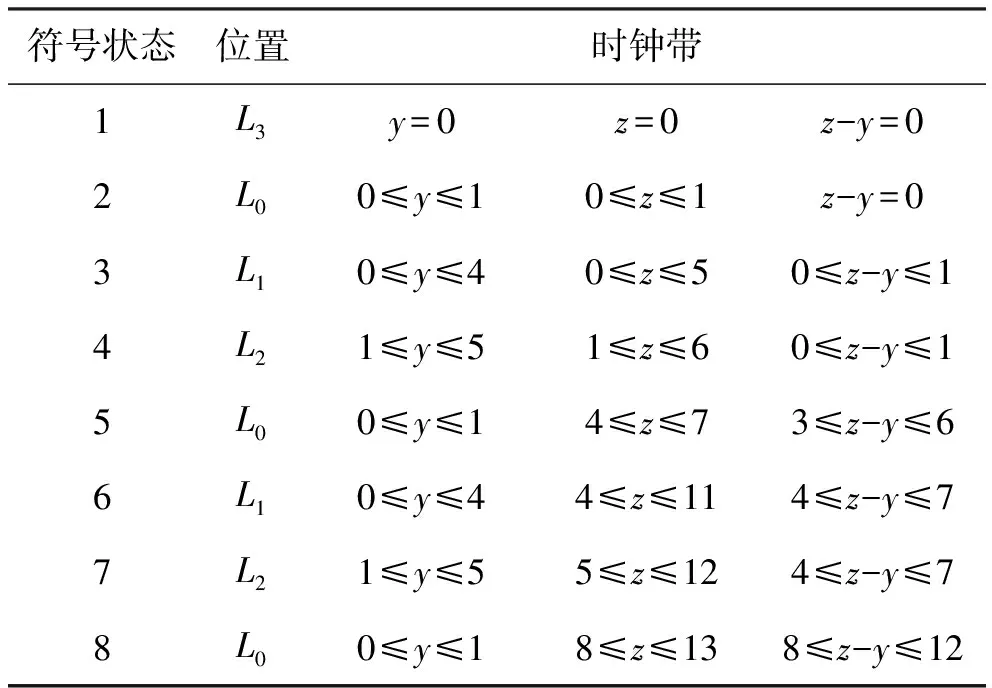
表1 前向符号状态搜索中时间自动机P得到的部分符号状态

图2是在前向符号状态搜索过程中时间自动机P在控制位置L0产生的时钟带，Di为第i次到达位置L0时的时钟带。可以看出在这个过程中出现了严重的片段问题，这是由于阈值LARGE较大，而时钟z的增长又比较缓慢。为了判断控制位置L4是否可达，时间自动机必须多次执行L0、L1、L2组成的环，才能使时钟z得到足够的增长。由于模型中出现了不同的时间度量，时间自动机在前向符号搜索进行模型检测时，状态空间会分裂成大量的时钟带片段，导致片段问题。

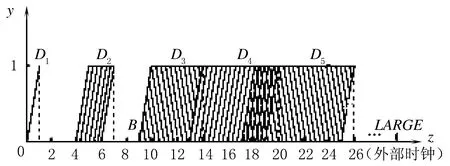
图2 时间自动机P在控制位置L0的时钟带

1.3 精确加速技术

研究工作者已经提出了多种精确加速方法，包括基于附加环和基于驻留环的精确加速方法，其关键技术在于为时间自动机的可加速环添加一个附加环，构造加速模型，从而实现加速[6]。这些方法不会改变时间自动机的可达性，可以有效加速前向搜索可达性分析，从而解决片段问题。

定义2(加速自动机) 假设M=(Loc,l0,X,A,I,E)是一个时间自动机，A(M,l,x,B)= (Loc∪{l′},l0,X,A,I′,E∪{e1,e2})(假设l′∉Loc)是M的一个加速自动机，其中，l∈Loc；常量B∈N，B=[a/(b-a)]*a；x∈X且(Ec,x)是一个可加速环；[a,b]是加速窗口；z是可加速环以外的时钟；I′=I∪{(l′,true)}；e1=(l,τ,x≥0,{x},l′)；e2=(l′,τ,z≥B,{x},l)。

根据可加速环的定义可知，图1中时间自动机P的控制环是一个可加速环，可以计算出它的加速窗口是[4,6]。根据定义2向时间自动机P添加一个驻留环，构造基于驻留环的加速自动机PA，其中x=y，可以计算出B=8。与图1相比，在图3中仅添加一个新位置L5。

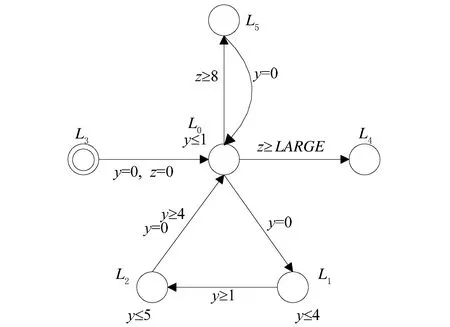
图3 时间自动机P的加速自动机PA

2 有效精确加速的判断条件

2.1 关键参数

在精确加速技术中，有几个关键的参数：加速窗口[a,b]、实际加速点B和阈值LARGE。

(1) 加速窗口[a,b]

每个可加速环都有一个加速窗口，它是指执行一次可加速环时钟值增加大小的区间，可以根据时间自动机的语法计算出来。只要窗口上界a严格小于窗口下界b，可加速环就会产生连续的时钟带[7]。图2中可加速环的加速窗口是[4, 6]，并且在z=8之后时钟带开始连续。

(2) 实际加速点B

根据文献[11]，精确加速的实际加速位置(图2中的B点)是由加速窗口决定的，其值为[a/(b-a)]*a。图2中的时钟带在z=8时开始连续，也就是说实际加速点B=8。

(3) 阈值LARGE

阈值LARGE是一个常数，通常把它作为跳出控制环的条件。正是因为LARGE的存在，使得模型中出现了不同的时间度量，导致可达性分析算法对控制环进行多次重复搜索。对于可加速环，若LARGE足够大(105以上)，则附加环有明显的加速效果。下文中将LARGE简记为L。

2.2 加速效果及加速代价分析

附加环的加速效益用加速效果和加速代价两个标准来衡量。

定义3(加速量及加速效果) 在一个含有可加速环的时间自动机中，[a,b]是加速窗口。添加附加环之前，为了达到阈值LARGE，可加速环需要运行m1次，m1是满足不等式n0+m1*a≥LARGE的最小值，其中，n0是环境时钟z执行可加速环之前的最大值。添加附加环之后，在满足附加环的入边条件之前，需要运行可加速环m2次，m2是满足不等式m2*a≥B的最小值。

加速量是指添加附加环之后减少的可加速环运行次数，用Nacc表示，其值为m1-m2。加速效果是指添加附加环之后节省的运行时间，也就是运行Nacc次可加速环需要的时间，用T+表示。

定理1 假设M是一个时间自动机，Ec是M的一个可加速环，加速窗口是[a,b]且a

证明 根据定义3，由不等式n0+m1*a≥LARGE可得，m1=[(L-n0)/a]=(L-n0)/a+γ1，其中0≤γ1<1。由不等式m2*a≥B可得，m2=[B/a]=B/a+γ2，其中0≤γ1<1。因此，m1-m2=(L-n0-B)/a+γ1-γ2。由0≤γ1、γ2<1可知，-1<γ1-γ2<1。由此可得，加速量Nacc=m1-m2存在最小值Nacc=(L-n0-B)/a-1。

推论1 假设M是一个时间自动机，存在窗口为[a,b]的可加速环，且a

加速量和加速效果说明精确加速技术能够减少可加速环的运行次数，节省可达性分析的时间，但是由于引入了附加环，可达性分析算法在每次运行到加速位置时都要对附加环的入边条件进行判断，直到条件满足，即到达实际加速点B，这一过程增加了运算量和运行时间。

定义4(加速代价) 假设M是一个时间自动机，Ec是M中的一个可加速环，加速窗口是[a,b]且a

2.3 有效加速的判断条件

利用上述定义和定理，分析精确加速技术有效加速的条件。用符号t表示搜索一个节点所需的时间，即单位时间，len表示可加速环的长度，即控制位置的个数。则加速效果T+的计算公式为：

T+=Nacc*t*len

(1)

根据加速代价的定义，在到达实际加速点之前，可达性分析算法在每次到达加速位置时都要判断附加环的入边条件是否成立，而这个判断时间就是单位处理时间t，根据定义4可知判断入边条件的次数为m2，则加速代价T-的计算公式为：

T-=m2·t

(2)

定理2 假设M是一个时间自动机，Ec是一个可加速环，加速窗口是[a,b]且a

证明 附加环能够有效加速前向可达性分析的条件是加速效果远远大于加速代价，也就是：T+>>T-，即Nacc*t*len>>m2*t，也即Nacc*len>>m2(t>0)。把Nacc和m2的值代入上式得

[(L-n0-B)/a-1]*len>>B/a+γ2

由于(L-B)/a-1>(L-n0-B)/a-1，B/a+γ2>B/a，所以[(L-B)/a-1]*len>>B/a，即：

B<

至此，得出了精确加速是否有效的判断条件：

B<

从这个判断条件可以看出，当可加速环的长度和加速窗口一定时，如果LARGE的值足够大，精确加速的效益就很明显。根据定理2，在识别出可加速环后，首先判断可加速环是否满足有效加速的条件，若不满足条件，则说明加速效果不理想，不用添加附加环；若满足条件，则说明可加速环能够进行有效加速，可以添加附加环。

2.4 实例验证

对图1中的时间自动机P进行分析，这里设定LARGE的值为300 000。

由位置L0、L1、L2组成的可加速环窗口为[4, 6]，B=8，len*(L-a)/(len+1)≈225 000，可以看出B<

对图4中的时间自动机P进行分析。LARGE值仍为300 000，由L0、L1、L2组成的可加速环窗口为[6 000,7 100]，B=[a/(b-a)]*a=36 000，len*(L-a)/(len+1)=3*(300 000-6 000)/(3+1)=220 500，可以看出B并不是远远小于len*(L-a)/(len+1)，因此加速条件不成立。根据定理2可以判断时间自动机P添加附加环之后加速效果不明显，无需构造加速模型。

图4 时间自动机P

利用模型验证工具UPPAAL，分别对时间自动机P和P′的可达性质E<>P.L4和E<>P.L4进行验证，表2给出了这两个自动机添加附加环前后所消耗的时间和空间对比。从表中数据可以看出，时间自动机P在添加附加环之后加速效益明显，但降低了验证速度。这个结果与定理2中的判断条件分析结果一致。

表2 验证可达性运行时的数据

3 结 语

本文通过对精确加速技术进行分析，利用加速效果和加速代价衡量附加环的加速效益，推导出了精确加速技术能够有效加速可达性分析的条件，根据这个加速条件可以判断是否有必要添加附加环。下一步的工作是对可达性分析算法进行改进以取得更好的加速效果，并对自动添加附加环构造加速模型进一步研究。

参考文献:

[1] Bouyer P, Markey N, Sankur O.Automata, Languages, and Programming [M].Berlin: Springer Berlin Heidelberg, 2012: 128-140.

[2] Pelánek R.Reduction and Abstraction Techniques for Model Checking [D].Brno：Masaryk University, 2006.

[3] Leroux J, Sutre G.Accelerated Data-flow Analysis[C]//Static Analysis.Belin: Springer Berlin Heidelberg, 2007: 184-199.

[4] Barnat J, Bauch P, Brim L, et al.Employing Multiple CUDA Devices to Accelerate LTL Model Checking [C]//2010 IEEE 16th International Conference on Parallel and Distributed Systems (ICPADS).Berlin: IEEE, 2010: 259-266.

[5] Qanadilo M, Samara S, Zhao Y.Accelerating Online Model Checking [C]//2013 Sixth Latin-American Symposium on Dependable Computing (LADC).Berlin: IEEE, 2013: 40-47.

[6] 尹传龙, 宋伟, 庄雷.识别时间自动机中可加速环的方法[J].计算机工程与设计, 2010, 31(23): 181-183.

[7] 尹传龙, 庄雷, 王从银.实时模型检测中基于驻留环的精确加速[J].电子学报, 2011, 39(3): 489-493.

[8] Cicirelli F, Furfaro A, Nigro L.Model Checking Time-dependent System Specifications Using Time Stream Petri Nets and UPPAAL [J].Applied Mathematics and Computation, 2012, 218(16): 8160-8186.

[9] Fehnker A, Van Glabbeek R, Höfner P, et al.Automated Analysis of AODV Using UPPAAL[C]//Tools and

Algorithms for the Construction and Analysis of Systems.Berlin: Springer Berlin Heidelberg, 2012: 173-187.

[10] 张松年, 庄雷, 杜娟.时间自动机可达性分析算法的改进[J].计算机工程与科学, 2007, 29(10): 44-46.

[11] Hendriks M, Larsen K G.Exact Acceleration of Real Time Model Checking [J].Electronic Notes in Theoretical Computer Science, 2002, 65(6): 120-139.