弧齿锥齿轮传动设计中数据的程序化处理
2014-04-01,,
,,
(中原工学院,郑州 450007)
弧齿锥齿轮具有承载能力高、运转平稳、噪声小、适应于高速传动等特点[1]。广泛应用于汽车、拖拉机、工程机械及其他机械上。在传统的弧齿锥齿轮传动计算中,所用数据资料均在设计手册中查找,数表查询完全由人工完成,查阅费时又容易出错。如何将手册中所需的数据、图表等内容形成计算机识别的数据文件,便于用户灵活检索和调用,成为目前研究的主要问题[2]。本文就格林森弧齿锥齿轮传动设计过程中复杂数据的计算机程序化处理进行探讨。
1 弧齿锥齿轮传动的设计流程
利用计算机辅助进行格林森弧齿锥齿轮传动设计的流程如图1所示,涉及的公式、数表、线图均来自于文献[3]。
文中涉及变量的说明:T-输入转矩;u0-传动比初值;∑-轴交角;d10-小齿轮大端分度圆直径;Z1-小齿轮齿数;Z2-大齿轮齿数;mi-齿轮大端模数;δ2-大齿轮分度锥角;b-齿宽;β0-大端螺旋角;KA-工况系数;KV-动载系数;KHβ-载荷分布系数;ZX、YX-尺寸系数;ZR-齿面光洁度系数;ZE-弹性系数;ZB、YB-温度系数;I、J-几何系数;δHlim-齿轮接触极限应力;δFlim-弯曲极限应力;SH-计算安全系数。
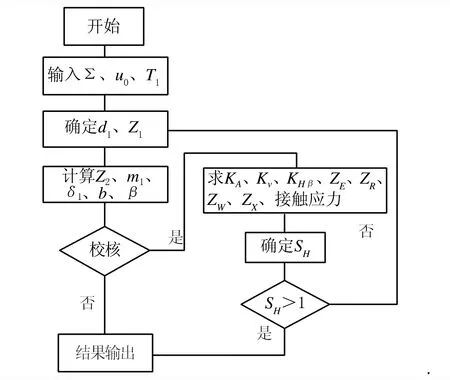
图1 格林森弧齿锥齿轮传动设计程序框图
上述变量可划分为数表和线图两类。对数表和线图的类型归类后,可对其进行计算机程序化处理。
2 数表的程序化
2.1 数表类型
在传统的齿轮传动设计中,大量数表常被采用,可归纳为2种类型。
(1)列表函数型数表。自变量与对应的值之间存在函数关系,可通过追本溯源找出原始公式或者利用插值法推导出数表的近似关系(见表1)。
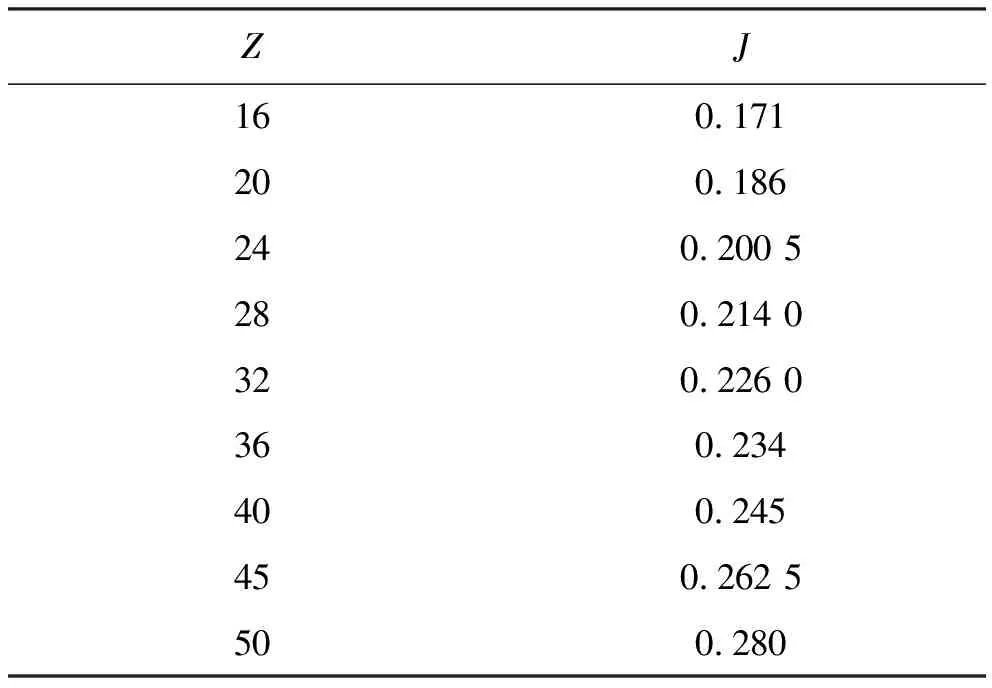
表1 弧齿锥齿轮几何系数
(2)非列表函数型数表。离散的自变量与对应的值之间没有函数关系,例如弧齿锥齿轮载荷分布系数。
2.2 数表的程序化
弧齿锥齿轮传动计算中涉及的数表多为一维和二维数表(见表2)。利用VB编程时,可将数表存入一维、二维或三维数组,通过查表、插值等方法检索所需数据。

表2 弧齿锥齿轮载荷分布系数KHβ
2.2.1 列表函数型数表的程序化
对于列表函数(见表1)型数表,因其有理论公式、经验公式或者近似关系式,所以在进行计算机辅助设计时,可还原为原始公式[4],采用计算公式编制程序。对于没有原始公式的数表,则需要在程序化设计过程中近似拟合出数表关系式,工程中通常采用最小二乘法进行拟合。
根据表1提供的齿数Z和齿形系数J的数据,可借用Matlab软件的Polyfit函数。其调用格式为:
p=polyfit(x,y,n)
(1)
其中:x,y为数表中对应的自变量与函数值;n为求解次数;p表示结果关系式中各项系数。
用Matlab求解公式程序如下:
Z=[16 20 24 28 32 36 40 45 50];%输入已知自变量;
J=[0.171 0.186 0.2005 0.2140 0.2260 0.234 0.245 0.2625 0.28];%输入已知函数值;
p=polyfit(Z,J,2);%用2次多项式拟合,求解多项式系数;
p=-0.000 006 0.003 48 0.118 61;%各项系数;
在程序编写中,弧齿锥齿轮齿形系数J与齿数Z的关系式可近似用公式(2)表示。
J=-0.000 006Z2+0.003 48Z+0.118 61
(2)
2.2.2 非列表函数型数表的程序化
对于非列表函数(见表2)型数表,因其自变量与对应的值之间没有函数关系,无法拟合出近似关系式,整个数表中是一系列数据的集合,所以在程序化时多采用汇编语言中的数组形式存储,检索时利用程序对数组数据查询即可。
如对弧齿锥齿轮载荷分布系数KHβ求解时,需要对表2进行程序化处理,可用二维数组K[i][j]表示, 其中第一个下标变量标识原动机类型, 第二个下标变量标识工作机类型。使用时只需输入原动机和工作机的工作类型代码i和j即可方便地检索出对应的KHβ值。
3 线图的程序化
3.1 线图的类型
在齿轮设计过程中, 需查阅大量的表示各参数间关系的线图, 如弧齿锥齿轮齿向载荷分布系数Zx、节点区域系数ZH等线图。这些线图包括直线、折线和各种曲线图, 归纳后可分为线图公式和线图数表2种类型。
3.2 线图的程序化处理
3.2.1 线图公式类型的程序化
在齿轮传动设计中,对具有原始公式的线图,可直接利用其公式来编制程序。例如,在对齿轮进行强度计算时,对弹性系数ZE、节点区域系数ZH等均可直接调用原始公式;对于由直线或折线组成的线图, 则可拟合成直线方程或指数方程。本文以确定D10为例,演示线图公式拟合过程。
在弧齿锥齿轮的初步设计中,用于估算D10的线图如图2所示。图中线型相对简单,直线大致平行,只是传动比不同,可将其拟合为统一公式。观察发现,横坐标小轮扭矩和纵坐标直径之间成对数关系,可方便地拟合出每条直线方程。其中一条直线可表示为:

图2 按齿面接触强度设计的小齿轮节圆直径与扭矩的关系图
lgdi=xlgTi+y
(3)
其中:x、y为常数;di、Ti分别为传动比为i时小齿轮大端节圆的直径和扭矩。但是因图中没给出齿数比,不能采用线性插值求解。对比分析图中的线型公式,不同齿数比线型公式更近似对数关系。为方便计算调用及编程,本文将公式进一步拟合为整体公式:
lgdi=0.325lgTi-0.125log2(N/n)-0.525
(4)
例如,当齿数比i=2,小齿轮扭矩T2=8 000 N·m,代入公式(4),计算值d2=4.186,查表值d2=4.2,计算误差为0.33%,符合计算精度[5]。其余类似线图亦可采用同样方法拟合出线图公式。
3.2.2 线图数表类型的程序化
线图数表类型的线图相对比较复杂,主要采用的处理方法是对曲线进行离散化处理后进行插值处理[6]。其具体步骤为:①先从线图中选出足够量的抽样点;②向坐标轴作垂线, 找出对应坐标值;③采用列表函数的处理方法输入计算机。
选点时应注意使各节点的函数值不致相差太大[6],当曲线斜率变化较大时,抽样节点取得密一些,当曲线斜率变化较小时,则可将节点取得疏一些。
4 结 语
本文对弧齿锥齿轮传动计算过程中所涉及的数表及线图处理方式进行了探讨,结合Matlab软件及汇编语言的相关模块,实现了弧齿锥齿轮传动设计中相关数据的程序化处理。对于复杂线图,亦可采用图片矢量化或人机交互的方式进行程序化处理。
参考文献:
[1] 张燕飞,高红梅.弧齿锥齿轮传动齿轮副侧隙调整[J].机械传动,2005,29(4):9-11.
[2] 库兰.机械设计在CAD中图表资料的处理[J].新疆大学学报(自然科学版),2002,19(2):246-250.
[3] 秦大同,谢里阳.现代机械设计手[M].第4卷.北京:化学工业出版社,2011.
[4] 么元昱,曾红,吕秀芳.机械CAD中数表与线图的处理方法[J].辽宁工业大学学报,2008,28(1):42-44.
[5] 罗月新,毛世民,吴序堂.准双曲面齿轮CAD中线图程序化处理的研究[J].机械科学与技术,1999,18(6):1027-1029.
[6] 王姝歆,陈国平.齿轮传动计算机辅助设计中图表资料的处理[J].机械设计与制造,2000,3(5):14-15.
