基于随机介质理论的隧道冻结期地表冻胀预测方法

蔡海兵 ，彭立敏，郑腾龙

(1. 安徽理工大学 土木建筑学院，安徽 淮南，232001；2. 中南大学 土木工程学院，湖南 长沙，410075)

20 世纪50 年代，Litwiniszyn[1]基于砂箱模型试验，为研究地下采矿过程中岩层与地表移动等问题而提出了随机介质理论，该理论将岩层视为一种“随机介质”，将地下开采所引起的岩层与地表变形看成是一随机过程，应用概率统计的方法可实现对岩层与地表变形的预估。随机介质理论经过Liu 等[2-3]的发展和完善，其应用领域从最初的地下采矿地表变形分析，发展到露天采矿、近地表开挖及地层疏水所引起的地表变形分析等。阳军生等[4]和杨小礼等[5]均针对城市隧道施工所引起的地表移动和变形问题，采用随机介质理论进行分析讨论，进一步拓展了随机介质理论的应用领域。施成华等[6]考虑隧道开挖地层移动与变形的时间－空间发展过程，基于随机介质理论，系统地对城市隧道矿山法及盾构法等施工引起的地层移动与变形相关问题进行了研究。目前该理论已成为我国城市地铁隧道工程中地表变形预测的实用方法之一。如将地层冻结引起的地表冻胀变形看成是一随机过程，该过程可以认为是岩土体开挖引起地表变形的逆过程，则隧道冻结施工引起的地表冻胀变形问题亦可以采用随机介质理论进行预测分析。阳军生等[4]、李方政[7]、陶德敬等[8]和周太全等[9]都采用该理论对地铁隧道冻结法施工引起的地表冻胀变形进行了分析，并得出了一些有意义的结论，但共同的不足之处为在分析过程中均未考虑冻结过程，即冻结壁的形成过程。本文作者考虑冻结壁的形成过程，基于随机介质理论，以圆形隧道全断面水平冻结工程为例，以建立隧道冻结期地表冻胀的预测方法。

1 地表冻胀的随机介质预测方法

1.1 冻结壁交圈前的预测方法

图1 所示为冻结壁形成过程图。开始冻结时，冷媒剂与冻结管周围的地层产生剧烈的热交换，在每个冻结管周围很快形成近似圆柱形的冻结岩土柱，如图1(a)所示；冻土柱进一步扩展，直至相邻冻土柱相互交圈，在隧道周围形成封闭的冻结壁，如图1(b)所示；交圈后，原各冻结管的冻结锋面连成向隧道内扩展的内冻结锋面和向隧道外扩展的外冻结锋面，且内、外冻结锋面很快趋于平滑，如图1(c)所示。

图2 所示为冻结壁交圈前坐标系转换图。假定隧道采用单圈全断面水平冻结，n 根冻结管均匀布置在同一圈径上，各冻结管所处的土层性质相同，由冻结壁的形成过程可知，冻结壁交圈前，经t 时刻后，在隧道周边形成n 个外半径为R(t)的冻土柱，各冻土柱形成过程中发生的体积膨胀均为半径从R(t)均匀膨胀至RΔ(t)，膨胀的各圆环柱截面积也均为Δ(t)，如图2所示。由随机介质理论可知[4]：对于平面问题，在εoη(xoz)直角坐标系下，单个冻土柱在t 时刻发生膨胀变形而引起的地表各点冻胀位移表达式为

图1 冻结壁形成过程图Fig.1 Formation processes of frozen wall

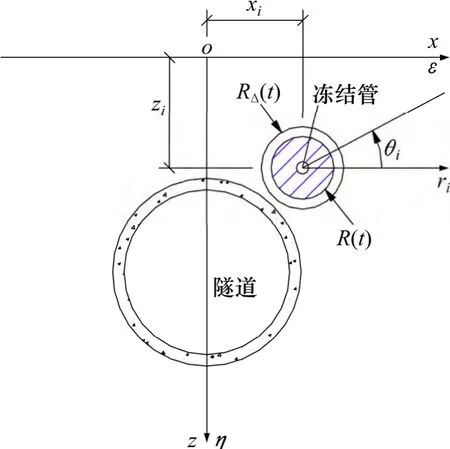
图2 冻结壁交圈前坐标系转换图Fig.2 Coordinate system transformation diagram before circle-crossing period of frozen wall

式中：β 为岩土层的主要影响角。

记各冻结管的编号为1，2，…，n，第i 根冻结管中心在εoη(xoz)直角坐标系下的横坐标为xi，纵坐标为zi，将εoη(xoz)直角坐标系变换到rioiθi极坐标系，如图2 所示，则转换公式为

式中：h 为隧道中心距地表的距离；Rd为冻结管布置圈半径。

由式(1)可得：在平面问题条件下，第i 根冻结管水平冻结引起地表各点冻胀位移表达式为

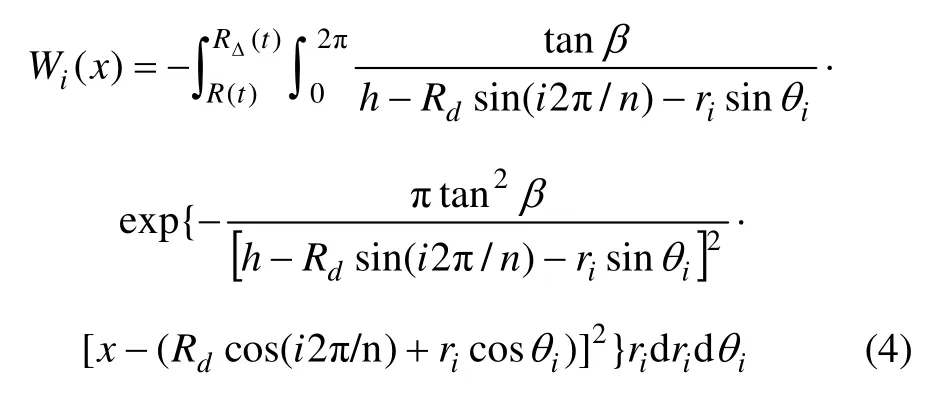
如忽略相邻冻结管冻结引起地表冻胀位移的相互影响，则在冻结壁交圈前，地表冻胀由多个冻土柱的叠加膨胀变形引起。由此，根据叠加原理，则有冻结壁交圈前的地表冻胀位移表达式为

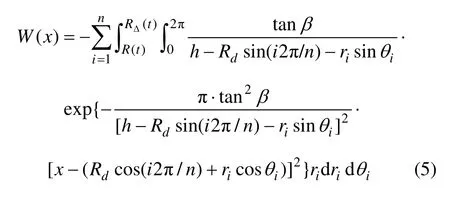
1.2 冻结壁交圈后的预测方法

图3 所示为冻结壁交圈后坐标系转换图。随着冻结时间的延长，隧道周边各冻土柱进一步扩展，相邻冻土柱相互交圈后即在隧道周边形成圆环柱状冻结壁，如图3 所示，冻结壁外锋面半径为R(t)，冻结壁扩展过程中的体积膨胀假定为从半径R(t)均匀膨胀至RΔ(t)，冻胀区域面积为Δ(t)。冻结壁交圈后，地表冻胀则由整个冻结壁膨胀变形引起。

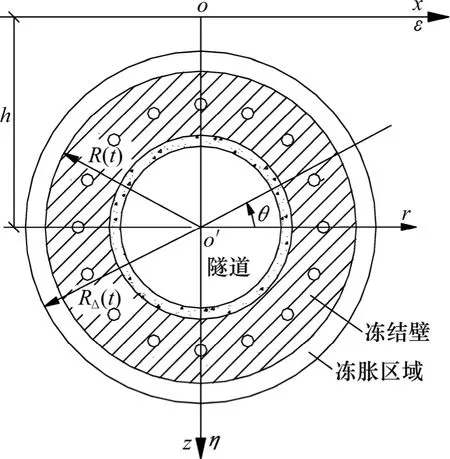
图3 冻结壁交圈后坐标系转换图Fig.3 Coordinate system transformation after circle-crossing period of frozen wall

将εoη(xoz)直角坐标系转换成ro′θ 极坐标系，则该两坐标系之间的转换公式为

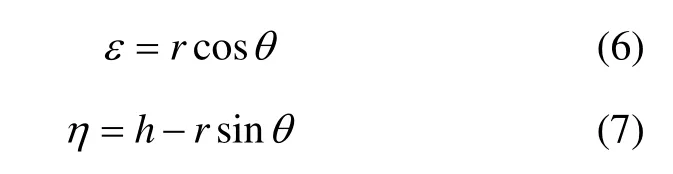
由式(1)可得在平面问题条件下，冻结壁交圈后的地表冻胀位移表达式为

当隧道采用全断面水平冻结法施工时，考虑冻结壁的形成过程，冻结壁交圈前采用式(5)预测地表各点的冻胀位移，冻结壁交圈后则采用式(8)预测地表各点的冻胀位移。

2 冻结外锋面半径的确定方法

在冻结壁交圈前，冻结外锋面半径R(t)为单个冻土柱的半径，在冻结壁交圈后，则为冻结壁外锋面半径。冻结壁交圈前、后冻结外锋面半径的确定问题即为单管冻结和多管冻结条件下温度场分布规律的求解问题。国内外众多科研学者对此问题进行了相关研究，总的来说，现有冻结温度场的计算理论主要包括平板冻结理论和单管冻结理论[10-11]，其中平板冻结理论为一维半无限域热传导问题，而单管冻结理论为二维热传导问题。冻结壁交圈后的瞬态温度场可由平板冻结理论近似求解，冻结壁交圈前的瞬态温度场则可由单管冻结理论近似求解。

2.1 平板冻结理论

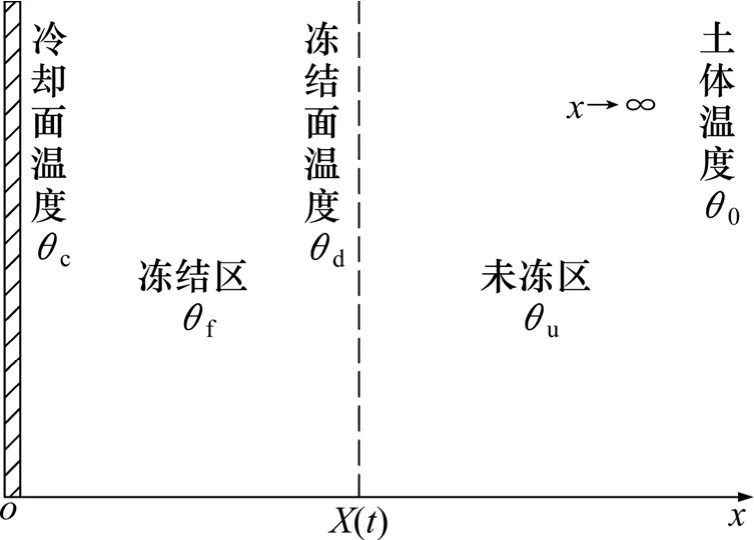
图4 平板冻结理论示意图Fig.4 Schematic diagram of flat-panel freezing theory

图4 所示为平板冻结理论示意图。将薄板垂直置入土中，假定薄板仅在其侧面与土体发生热交换，其顶、底面均与土体不发生热交换，薄板冷却面温度为θc且保持恒定，冻结区土体温度为θf，未冻区土体温度为θu，均为时间t 和坐标x 的函数。冻结锋面为一移动的相变边界，其与冷却面的距离为X(t)，且在冻结锋面处，土体冻结温度θd=0 ℃。

对于该一维半无限域热传导问题，冻结区和未冻区微分方程可写为

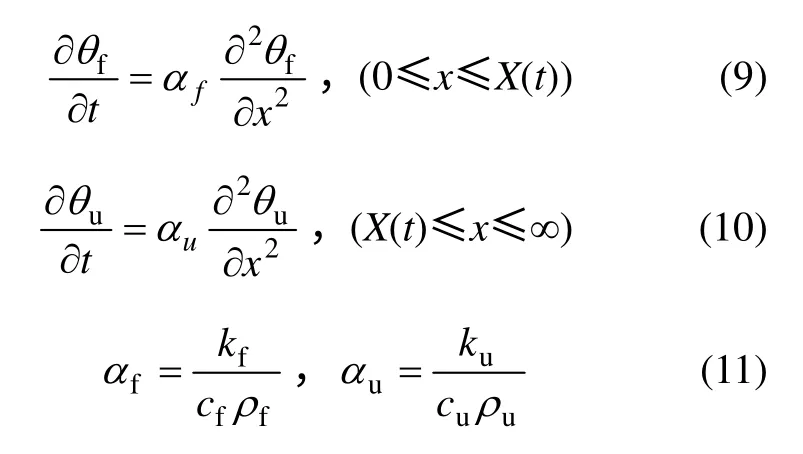
式中：αf和αu分别为冻结区、未冻区土体的热扩散系数，m2/d；kf和ku分别为冻土和未冻土的导热系数，kJ/(m·d·℃)；cf和cu分别为冻土和未冻土的比热容，kJ/(kg·℃)；ρf和ρu分别为冻土和未冻土的饱和密度，kg/m3。

微分方程的初始条件为

式中：θ0为土体初始温度。

微分方程的边界条件为：

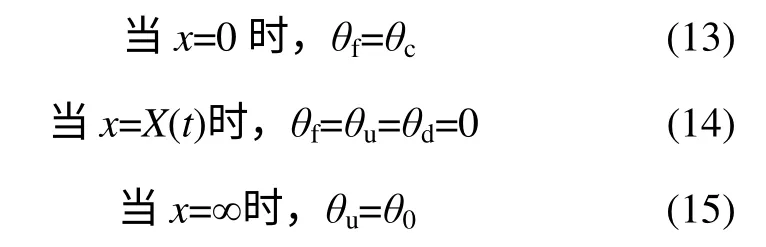
除上述边界条件外，在冻结锋面，即相变边界面X(t)处的热平衡方程为

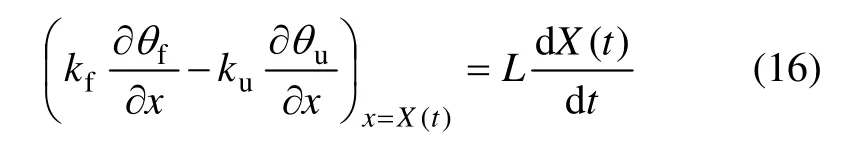
式中：L 为单位容积土体的相变潜热，kJ/m3，由下式给出：

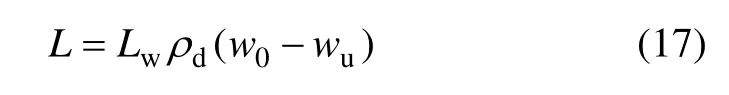
式中：Lw为单位质量水的相变潜热；ρd为土体的干密度，kg/m3；w0为土体的初始含水量；wu为冻土中未冻水含量。

结合上述初始条件和边界条件，对微分方程进行求解，则可得冻结锋面X(t)与冻结时间的平方根成正比，即：

式中：A 为待定常数，需满足下式

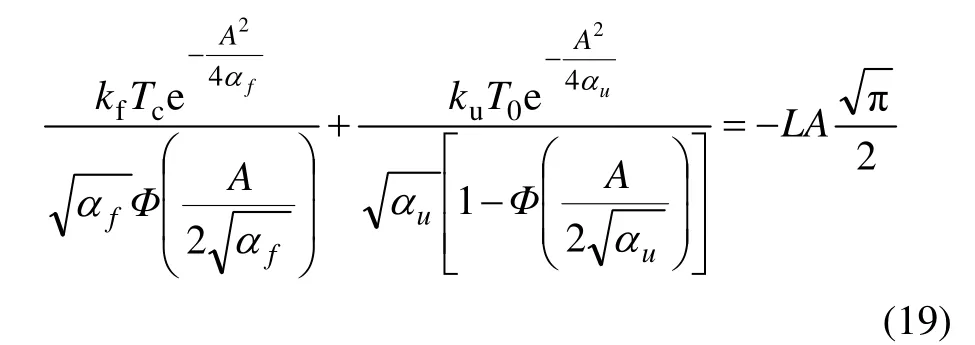
式中：Φ(y)为高斯误差函数，且有：

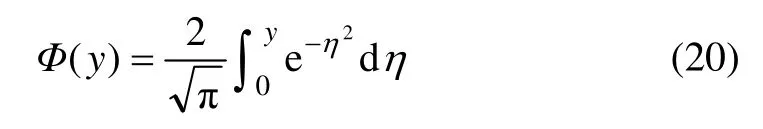
实际的冻结工程一般都依靠多根冻结管来形成冻结壁，冻结壁交圈后的温度场可由平板冻结理论近似求解。当未冻土和冻土的导热系数、比热容、密度等热物理参数由室内试验获取后，冻结锋面位置可采用式(18)和(19)计算。若已知冻结管布置圈半径Rd，则冻结外锋面半径R(t)、内锋面半径R1(t)可按下式计算：

2.2 单管冻结理论

冻结壁交圈前的温度场则由单管冻结理论进行求解，如图5 所示，根据冻结锋面将温度场分成冻结区和未冻结区，冻结区土体温度为θf，未冻区土体温度为θu，均为时间t 和径向坐标r 的函数，冻结锋面半径为R(t)，且冻结锋面处土体冻结温度θd=0 ℃。冻结管外半径为Rp，冻结管热流密度为Q(kJ/(m·d))。

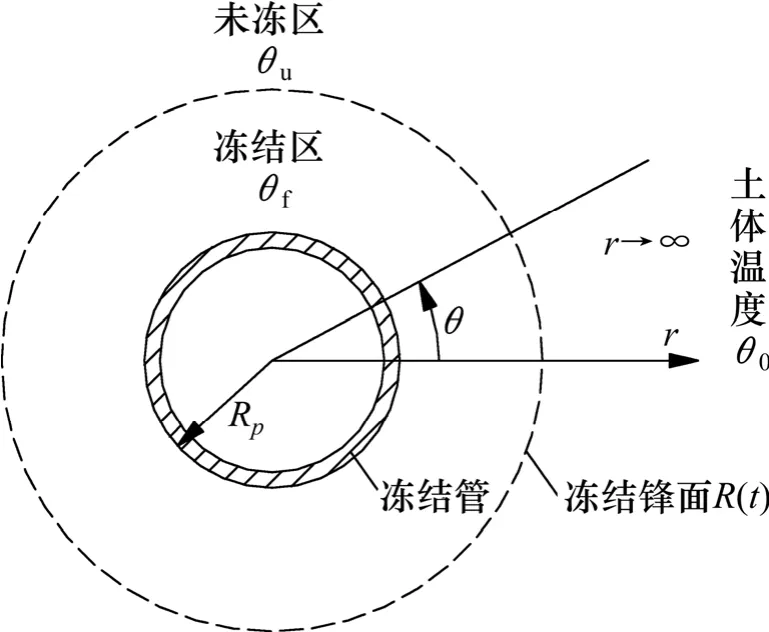
图5 单管冻结理论示意图Fig.5 Schematic diagram of single pipe freezing theory

对于该二维热传导问题，冻结区和未冻区微分方程可写为

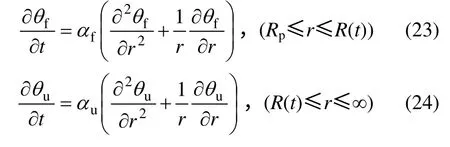
微分方程的初始条件为

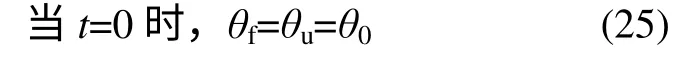
微分方程的边界条件为

在相变边界面R(t)处的热平衡方程为

这种模式不仅能保障购房者的基本住房需求，更能有效化解资金流动性风险，具体表现在两个方面。一是维护公积金制度设立初衷，有效保障中低收入群体的购房贷款需求。这种模式对中低收入群体是一种保护，尤其对效益不好的单位的职工而言，如果不实行该模式，他们会因单位缴存基数下降而无法享受公积金购房政策。二是可以盘活资金使用效率，减少资金使用风险。在这种模式下，通过分析职工的购房面积和购房实际需求，来调整公积金额度，既能增加市场上个人贷款资金的供应总量，也提高了公积金贷款对区域居民的覆盖率。

结合上述初始条件和边界条件，对微分方程进行求解，则可得冻结锋面半径R(t)与冻结时间的平方根也成正比，即：

式中：B 为待定常数，需满足下式

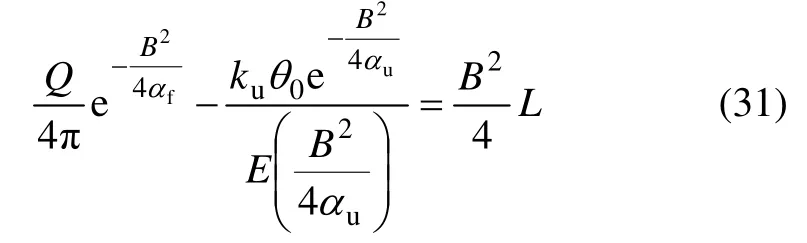
式中：E(y)为指数积分函数，且有

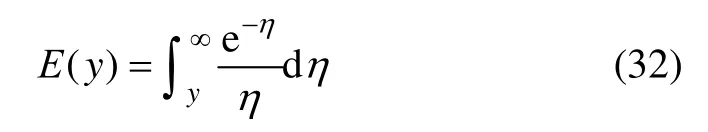
冻结壁交圈前的温度场可由单管冻结理论近似求解，由单管冻结理论可知，当未冻土和冻土的热物理参数确定后，单管冻结条件下冻结外锋面半径可采用式(30)和(31)进行计算，冻结内锋面半径即为冻结管外半径Rp。

相邻冻土柱的冻结锋面开始重叠，即意味着冻结壁刚好交圈，则冻结壁交圈时间可由下式计算：

式中：tj为冻结壁交圈时间；l 为相邻冻结管间距。

3 冻胀区域外半径的确定方法

工程中反映土体冻胀强弱的指标一般采用冻胀率，它是指土体试样在无侧向变形无纵向荷载条件下，经单向冻结，其纵向的高度增量与试样原高度的比

式中：εf为土体冻胀率；Δhf为试样纵向冻胀量；h 为试样原高度。

据其原理，假定冻结壁向外均匀膨胀，在冻结壁交圈前，冻胀区域外半径由下式计算：

在冻结壁交圈后，冻胀区域外半径由下式计算：

4 工程案例计算及分析

广州地铁3 号线天河客运站折返线隧道断面为马蹄形，长138.8 m，宽11.4 m，高9.146 m，埋深8～10 m，属于浅埋大断面隧道。由于该隧道斜下穿广汕公路和沙河立交桥，不能采用明挖法施工，最终采用选择全断面水平冻结暗挖法施工。

隧道水平冻结长度为138.8 m，分南、北两段施工，南、北段冻结长度均为71.9 m，末端搭接冻结长度为5 m。南、北端均在距隧道开挖边界1 m 处布置一圈冻结孔，冻结孔孔数为46 个，冻结孔间距为700～950 mm，南、北端冻结孔错位布置。冻结壁有效厚度设计值为2.5 m，冻结壁设计平均温度为-8 ℃，积极冻结期约为150 d[13]。隧道北端冻结孔布置设计如图6所示。

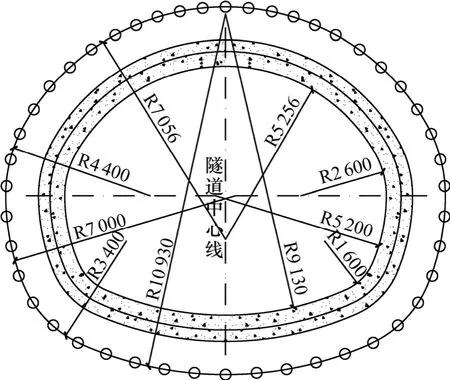
图6 隧道北端冻结孔布置图Fig.6 Freezing hole design at northern end of tunnel

隧道断面及冻结管布置圈均为五心圆拱线形，为计算简便起见，采用等代圆方法将其简化成圆形，经简化后的隧道外半径为5.137 m，冻结管圆形布置圈半径为6.137 m，相邻管间距为0.838 m。

根据折返线隧道岩土层分布情况，结合隧道及冻结壁的所处位置，在现场针对具有代表性的土层钻取土样，然后进行人工冻土物理力学性能试验，鉴于对地表冻胀位移起决定作用的冻结管主要位于可塑砂质黏土层中[13-14]，因此，本次预测分析中所需输入的热物理力学参数按该土层进行取值，如表1 所示。

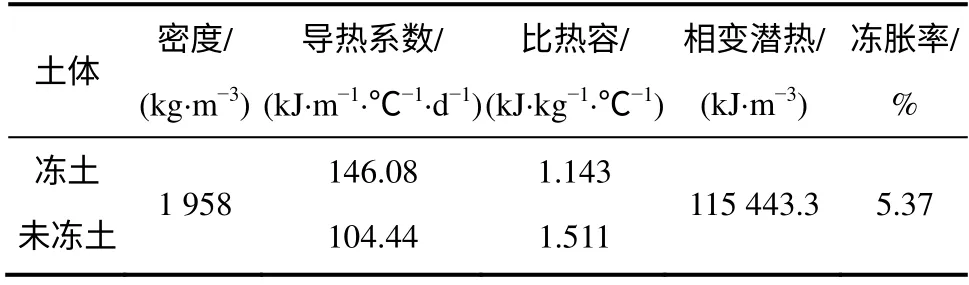
表1 土体热物理力学参数Table 1 Thermophysical parameters of soil

由于该隧道相邻冻结管平均间距仅为0.838 m，冻结壁交圈时间小于10 d，因此仅采用冻结壁交圈后的冻胀预测方法进行分析。

在分析中，考虑到隧道断面大，地表冻胀主要影响范围取为45 m，隧道轴线埋深为14.728 m，则土层主要影响角度的正切值tan β 为0.327。

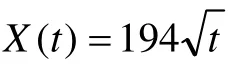
该浅埋大断面地铁隧道实际冻结施工中，共布置了28 个地表变形测点，其中15 和10-1 号测点均位于隧道中心轴线处[15]，16，17 号测点与15 号测点位于同一断面上，与隧道中心水平距离分别约为8 和15 m。

采用自行编制的地表冻胀Maple 计算程序，地表计算区域选为0≤x≤40 m，得到隧道积极冻结150 d后，地表冻胀位移分布规律的理论分析与现场实测结果对比如图7 所示。

由图7 可知：隧道积极冻结150 d 后，地表冻胀位移分布规律的理论分析结果较现场实测结果(15 号、16 号和17 号测点)稍大一些，但可大致反应实际情况，如对比隧道中心轴线处地表冻胀位移(距隧道中心水平距离为0 m)，现场实测结果(15 号测点)为317 mm，理论分析结果为350 mm，二者相差33 mm，与冻胀位移相比，该差尚可忽略。地表冻胀位移随机介质理论分析中，对隧道断面及岩土分层均在一定程度上进行了简化，特别是热物理参数主要参考可塑砂质黏土层进行取值，相对于其他土层，该土层的冻胀率最大，这也是地表冻胀位移理论分析结果较现场实测略大的主要原因。而同样位于隧道中心轴线处地表的10-1 号测点，其实测的冻胀位移达到近400 mm，这是因为该测点刚好布置在折返线隧道中部处地表，且在隧道中部，南、北端冻结管有约5 m 长的搭接范围，从而造成 10-1 号测点的冻胀位移在所有测点中最大[12,14]。

图7 冻结150 d 后地表冻胀位移分布Fig.7 Surface frost heave displacements distribution after freezing 150 d

积极冻结期内，隧道中心轴线处地表历时冻胀位移的理论分析与现场实测结果对比如图8 所示。

图8 表明，在地表冻胀位移随冻结时间的变化方面，理论分析与现场实测结果(15 号测点) 吻合，总体表现为，在冻结初期，冻胀位移增长速度较快，而到冻结后期，冻胀位移随时间呈相对缓慢增长趋势。10-1号测点因其所处的特殊位置，其冻胀速度最快。

地表冻胀位移的对比分析结果验证了本文所提出的随机介质预测方法的可靠性，且该方法用于工程实际均具有较高的精确性。

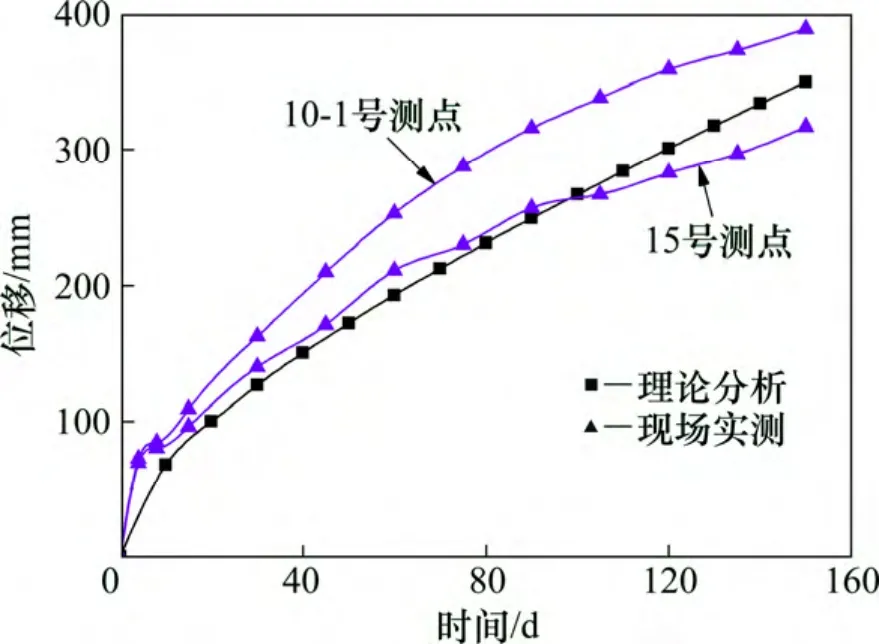
图8 隧道中心轴线处地表历时冻胀位移Fig.8 Surface frost heave displacements with time at central axis of tunnel

5 结论

1) 在隧道水平冻结期，冻结壁交圈前，地表冻胀位移由多个独立冻土柱的叠加冻胀效应引起，冻结壁交圈后，地表冻胀位移则由整个冻结壁的冻胀效应引起。据此，考虑冻结壁的形成过程，基于随机介质理论，推导了地表冻胀位移的计算表达式，建立了地表冻胀的预测方法。

2) 对冻结外锋面半径和冻胀区域外半径这2 个关键参数的取值方法进行了探讨。提出冻结壁交圈前的瞬态温度场则可由单管冻结理论近似求解，冻结壁交圈后的瞬态温度场可由平板冻结理论近似求解，得出多管冻结交圈条件下冻结壁的扩展厚度(单管冻结条件下的冻土柱半径)与冻结时间的平方根成正比，并基于平板冻结理论和单管冻结理论，确定了冻结外锋面半径的计算方法，并在此基础上，导出了根据土体冻胀率、冻结内、外锋面半径计算冻胀区域外半径的解析方法。

3) 将所提出的地表冻胀随机介质预测方法应用于实际工程案例中，通过与现场实测结果的对比分析，验证了该预测方法的可靠性。

[1] Litwiniszyn J. Fundamental principles of the mechanics of stochastic medium[C]//Proceedings of the 3rd Conference on Theoretical Applied Mechanics. Bangalore, India, 1957: 18-26.

[2] LIU Baochen. Ground surface movement due to underground excavation in China[C]//Comprehensive Rock Engineering. New York: Pergaman Press, 1993: 781-817.

[3] 刘宝琛, 张家生. 近地表开挖引起的地表沉降的随机介质方法[J]. 岩石力学与工程学报, 1995, 14(4): 289-296.LIU Baochen, ZHANG Jiasheng. Stochastic medium calculating method of surface settlement caused by near surface excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 1995, 14(4): 289-296.

[4] 阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M].北京: 中国铁道出版社, 2002: 10-19.YANG Junsheng, LIU Baochen. Ground movement and deformation induced by urban tunnel construction[M]. Beijing:China Railway Publishing House, 2002: 10-19.

[5] YANG Xiaoli, WANG Jinming. Ground movement prediction for tunnels using simplified procedure[J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462-471.

[6] 施成华, 彭立敏, 雷明锋, 等. 浅埋隧道施工地层变形时空统一预测理论与应用[M]. 北京: 科学出版社, 2010: 18-30.SHI Chenghua, PENG Limin, LEI Mingfeng, et al. Time space united prediction theory and application of stratum deformation caused by shallow tunnel excavation[M]. Beijing: Science Press,2010: 18-30.

[7] 李方政. 土体冻胀与地基梁相互作用的叠加法研究[J]. 岩土力学, 2009, 30(1): 79-85.LI Fangzheng. Research on superposition method of interaction between soil frost heave and beams on foundation[J]. Rock and Soil Mechanics, 2009, 30(1): 79-85.

[8] 陶德敬, 王明年, 刘大刚. 冻结法隧道施工引起的地表移动及变形预测[J]. 现代隧道技术, 2006, 43(6): 45-50.TAO Dejing, WANG Mingnian, LIU Dagang. Prediction of surface movement and deformation caused by freezing method construction of tunnels[J]. Modern Tunnelling Technology, 2006,43(6): 45-50.

[9] 周太全, 华渊, 吕宝华. 某地铁区间隧道冻结施工冻胀效应随机预测分析[J]. 冰川冻土, 2009, 31(1): 119-123.ZHOU Taiquan, HUA Yuan, LÜ Baohua. Stochastic prediction for frost heave effect of a subway tunnel[J]. Journal of Glaciology and Geocryology, 2009, 31(1): 119-123.

[10] 蒋斌松, 王金鸽, 周国庆. 单管冻结温度场解析计算[J]. 中国矿业大学学报, 2009, 38(4): 463-466.JIANG Binsong, WANG Jinge, ZHOU Guoqing. Analytical calculation of temperature field around a single freezing pipe[J].Journal of China University of Mining & Technology, 2009,38(4): 463-466.

[11] Lunardini V J, Varotta R. Approximate solution to Neumann problem for soil systems[J]. Journal of Energy Resources Technology, 1981, 103(1): 76-82.

[12] 刘鸿绪. 对土冻结过程中若干冻胀力学问题的商榷[J]. 冰川冻土, 1990, 12(3): 269-280.LIU Hongxu. Discussion of frost heave mechanics problems in soil freezing process[J]. Journal of Glaciology and Geocryology,1990, 12(3): 269-280.

[13] 蔡海兵, 彭立敏, 郑腾龙. 隧道水平冻结施工引起地表冻胀的历时预测模型[J]. 岩土力学, 2012, 33(6): 1761-1768.CAI Haibing, PENG Limin, ZHENG Tenglong. A duration prediction model of surface frost heave induced by tunnelling with horizontal freezing method[J]. Rock and Soil Mechanics,2012, 33(6): 1761-1768.

[14] 姚直书. 蔡海兵, 程桦, 等. 采用长距离水平冻结暗挖法的浅埋大断面地铁隧道施工技术[J]. 中国铁道科学, 2011, 32(1):75-80.YAO Zhishu, CAI Haibing, CHENG Hua, et al. Multiparameter monitoring of frozen soil structure with super- long freezing hole drilling in Guangzhou metro[J]. China Railway Science, 2011, 32(1): 75-80.

[15] 姜耀东, 赵毅鑫, 周罡, 等. 广州地铁超长水平冻结多参量监测分析[J]. 岩土力学, 2010, 31(1): 158-164, 173.JIANG Yaodong, ZHAO Yixin, ZHOU Gang, et al.Multi-parameter monitoring of frozen soil structure with super-long freezing hole drilling in Guangzhou metro[J]. Rock and Soil Mechanics, 2010, 31(1): 158-164, 173.