光伏冷却系统微结构流动损失特性的熵产分析方法

张昊春，李 垚，韩 俊，王洪杰，严利明，秦 江

(1.哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001; 2.哈尔滨工业大学 复合材料研究所，黑龙江 哈尔滨 150001)

0 引言

光伏发电PV(Photovoltaic)是利用光生伏特效应将太阳能转化为电能的可再生能源技术，其关键部件为太阳能电池(Solar Cell)，PV具有可靠性强、地域限制少、低温室气体排放、可分布式发电、建设周期短的优点［1］，在多个领域内得到了广泛的应用［2－3］。

影响太阳能电池效率的主要因素为热损失，主要包括被吸收的光生载流子通过向能带释放声子的形式将大于禁带宽度的那部分能量损失掉和能量小于禁带宽度的光子不能被吸收所造成的损失。如果不对PV模块进行有效的冷却，电池板会因为大量吸收太阳辐射能处于红外波段的能量，产生热效应从而造成电池板温度升高，继而降低电池的转化效率［1］。热设计是影响光伏电池转换效率和发电系统稳定运行的重要影响因素［4－5］。此外，如果光伏电池高温工况持续的时间较长，则会出现不可逆的损坏。研究表明，电池每温度升高1℃，效率下降0.35%［6］。特别是对于聚光型光伏电池而言，其技术发展中面临高太阳能聚集面积、高热流密度和非均匀温度分布的挑战。近年来，国际国内已发展出多种太阳能电池板的冷却技术［7］。其中，微通道冷却技术［8］具有适应面广、冷却效率高和低功耗的优点，有着广阔的应用前景，得到了迅速发展。因此，为提高光伏电池的光电转换效率，需要对其冷却系统进行深入的性能评估［9－10］。

在光伏发电系统的微通道冷却结构中，工质处于微流动状态，对能量损失影响最大的是流动系统中各种不同形状的局部微结构，包括突扩、突缩、渐缩、渐扩、三通等。对于这些微流动器件来说，如何定量研究其功率损失是提高微流动系统性能的关键问题［11－13］。

本文基于热力学第二定律的熵产分析方法(EPA，Entropy Production Analysis)，以光伏电池冷却系统内渐缩圆管微结构为研究对象，提出了确定功率损失系数的算法流程。基于CFD数值模拟结果和EPA模型，得到了功率损失系数与雷诺数的关联方程式。

1 微通道内流动损失的EPA模型

1.1 EPA基本方程

微通道内，流体的流动通常处于层流区域。根据文献［14］，直角坐标系中，流场的局部熵产率可通过求解式(1)得到

通过式(1)，可求得流场每个子区域的熵产率。在此基础上，沿流场的体积V进行积分，可以得到流场的总体熵产率，即式(2)

继而可以得到流场体积V内的流动的功率损失(能量损失)［11］，如式(3)

总体来说，功率损失的求解通过如下步骤完成: (a)通过数值模拟对流场进行N－S方程的求解，得到管路速度场的分布;(b)运用式(1)，求解流道内的局部熵产率，继而求得整个流动管道的功率损失。

1.2 微流动结构的几何形状

本文主要讨论圆管渐缩流动的微结构，如图1所示。其中，微流动系统的几何尺寸为:D1=1 cm，L1=10 cm，L2=0.5 cm，L3=10 cm，D1/D2=2。

图1 微流动结构的几何形状Fig.1 Configuration of themicro－scale fluid structure

1.3 功率损失系数

对于图1所示的微流动系统，总的功率损失可以表示为如下形式

考虑图1所示的微结构，对于层流发展段，直管段L1和L3的功率损失可通过分析解得到，详细的推导过程参考文献［15］，同时有

其中

局部结构L2的功率损失无法通过解析的方式给出，但可以通过先数值求解φ，然后减去φL1和φL3得到。

为了能够有效的表征微局部结构流动损失特性，本文采用功率损失系数 ζ，具体表达式如下［11－13］:

根据式(7)可以得到

考虑雷诺数Re的定义式

可以得到

根据质量流率的计算公式m·=ρumA，可推得如下表达式:

将式(10)和式(11)代入式(8)，可以得到关于局部微结构的功率损失系数的表达式:

通过式(12)可以看出，功率损失系数与Re密切相关，下面将讨论如何将ζ与Re相关联起来。

1.4 功率损失系数与雷诺数的关联式

根据文献［11］，对于渐扩结构的微流动结构，存在雷诺数范围Re∈{1，500}内的ζ～Re关联式。在本文中，虽然微结构不同，但是物理流动机理与文献［11－12］相似。因此，假设ζ～Re存在如下关系:

选取如下目标函数:

根据式(14)，结合计算数据，通过曲线拟合的方法确定C1和C2，从而得到功率损失系数的函数关系式。

2 计算结果及讨论

以空气作为工质，T=20℃，密度ρ=1.188 kg/ m3，动力粘度ν=1.535×10－5m2/s。为了得到ζ～Re的关联式，需要得到不同Re数的功率损失情况。

假设流动处于充分发展的层流，在此条件下，保持动力粘度不变，改变入口处截面的平均速度可以获得Re数的不同量值，本文中选取的Re数及其对应的入口处平均速度参见表1。

表1 雷诺数及其对应的入口速度条件Table.1 Reynolds numbers and its corresponding inlet velocity condition

计算的总体流程为:首先利用CFD软件Open-FOAM中的SIMPLE算法进行流场计算，然后根据式(1)进行熵产率计算，进而求解功率损失。

为了验证结果的网格独立性，本文选取Gd1，Gd2，Gd3和Gd4作为不同计算网格数的标识，相应的网格质量参数如表2所示。

表2 网格质量参数Table.2 Quality parameter of the grids

计算时处理器为Inter®Xeon®CPU E5430@ 2.66 GHz，通常一个对每个Re数算例需耗时4天，计算平台为 openSUSE12.1，采用多组Re数并行计算。

图2给出了不同雷诺数，不同网格数下，系统总体的功率损失的分布曲线。

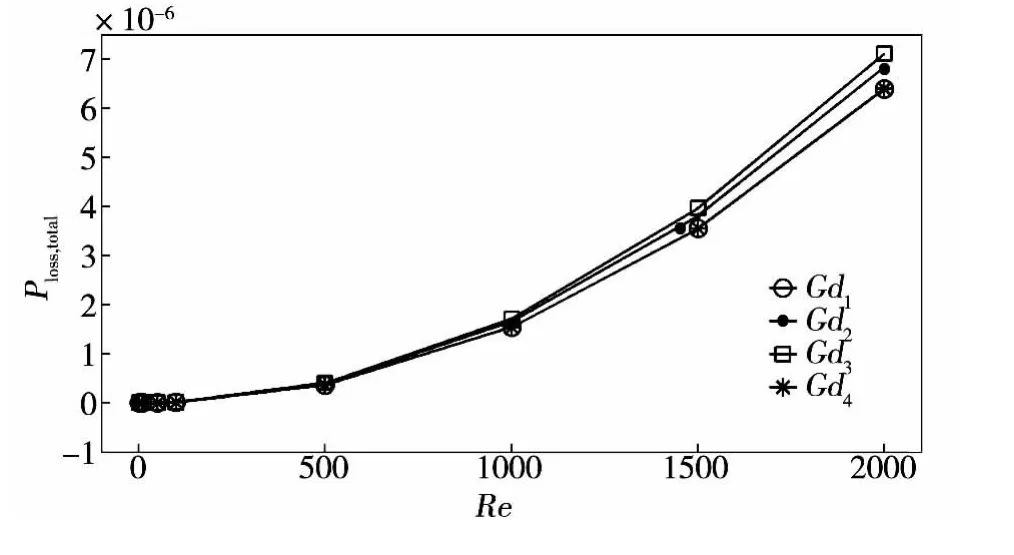
图2 总体功率损失Ploss，total与雷诺数Re的关系Fig.2 Relationship between total power loss PLoss，total and Reynolds numbers Re

从图2可以看出，当雷诺数Re小于100的时候，系统总体功率损失变化很小，当雷诺数Re处于100～2 000范围内时，系统功率损失随Re的增大而增大。

图3给出了不同雷诺数Re在不同网格数下，局部结构L2的功率损失分布曲线。

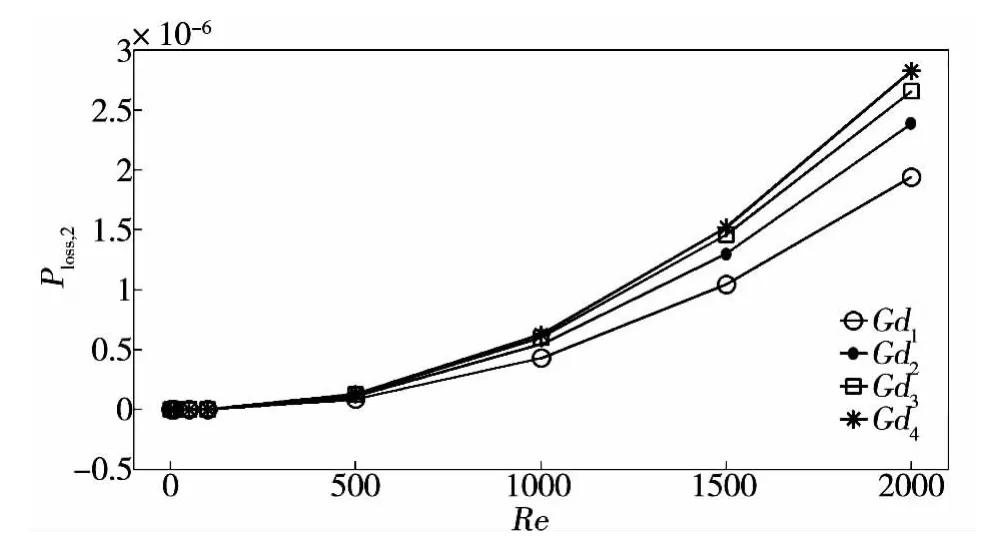
图3 局部微结构功率损失Ploss，2与雷诺数Re的关系Fig.3 Relationship between local power loss Ploss，2 and Reynolds numbers Re

从图3可以看出，当雷诺数Re小于100的时候，局部功率损失变化很小，当雷诺数Re处于100～2 000范围内时，局部功率损失随Re的增大而增大。图3和图2的功率损失随雷诺数区间分布趋势一致，表明对系统熵产影响最大的因素是局部结构所引起的机械能耗散，继而引起功率损失。

图4 不同雷诺数Re与ζ的关系曲线Fig.4 The correlation curve between various Reynolds numbers Re andζ

图4给出了ζ～Re的关系，可以看出，当Re小于1 000时，ζ随Re的增加而减小，而当1 000＜Re＜2 000时，ζ随Re的变化幅度较小，总体趋势符合ζ=的假设关系。

通过进行曲线拟合，得到C1=0.43，C2=19.5，因此，ζ的表达式为

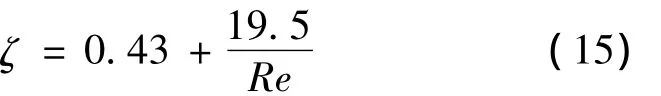
图6给出了拟合曲线的精度，可以看出，拟合曲线的精度较高。

3 结论

图5 ζ与Re的拟合关系曲线Fig.5 The curve fitting betweenζand Reynolds numbers Re

图6 曲线拟合的精度分析Fig.6 Accuracy estimation of curve fitting

对于光伏发电PV来说，温度是影响光伏电池转换效率和发电系统稳定运行的重要影响因素，为提高光伏电池的光电转换效率，需要对其冷却系统进行深入的性能评估。对于微流动器件的局部结构来说，如何定量研究其功率损失是提高微流动系统性能的关键问题。

本文基于热力学第二定律的熵产分析方法EPA，以光伏电池冷却系统内渐缩圆管微结构为研究对象，提出了确定功率损失系数的算法。同时，基于CFD数值模拟结果和EPA模型，发展了Re∈{1，2000}范围内功率损失系数与雷诺数的关联方程式。

当雷诺数Re小于100的时候，系统总体功率损失变化很小，当雷诺数Re处于100～2 000范围内时，系统功率损失随Re的增大而增大。当雷诺数Re小于100的时候，局部功率损失变化很小，当雷诺数Re处于100～2 000范围内时，局部功率损失随Re的增大而增大，对微通道系统熵产贡献最大的是局部结构所引起的机械能耗散。

由计算数据和数值方法，可以得到ζ～Re的关系。当Re小于1 000时，ζ随Re的增加而减小，而当1000＜Re＜2 000时，ζ随Re的变化幅度较小。本文得到的表达式为ζ=0.43+，符合ζ=C+1的趋势，其在Re∈{1，2000}范围内有较高的精度。

符号表

［1］Markvart T..Solar electricity，2nded.［M］.Wiley，New York，2000.

［2］张雪莉，刘其辉，马会萌，等.光伏电站输出功率影响因素分析［J］.电网与清洁能源，2012，28(5):75－81.

［3］党克，杨淮湘，严干贵，等.光伏发电系统MPPT改进方法研究［J］.电网与清洁能源，2013，29(4):91－95.

［4］毕二朋，胡明辅，袁江，等.光伏系统设计中太阳辐射强度影响的分析［J］.节能技术，2012，30(1):45－47，51.

［5］于炳霞，谭志萍，萑方，等.光伏发电功率预测自适应建模方法研究［J］.电网与清洁能源，2013，29(1):70－73.

［6］Coventry J.S..Performance of a concentrating photovoltaic/thermal solar collector［J］.J.Solar Energy，2005，78: 221－222.

［7］Ho T.，Mao S.S.，Greif R..The impact of cooling on cell temperature and the practical solar concentration limits for photovoltaics［J］.International Journal of Energy Research，2011，35(14):1250－1257.

［8］Tuckerman D.B.，Pease R.F.W..High performance heat sink for VLSI［J］.IEEE Electron Device Letters，1982，2 (5):126－129.

［9］Joshi A.S.，Dincer I.，Reddy B.V.，Performance analysis of photovoltaic systems:A review［J］.Renewable and Sustainable Energy Reviews，2009，13，1884－1897.

［10］艾英枝，王样强，李霸军，等.光伏电站不同统计时段计算的发电量对比分析［J］.电网与清洁能源，2012，28 (11):85－89.

［11］Zhang H.C.，Schmandt B.，Herwig H..Determination of loss coefficients formicro－flow devices:amethod based on the second law analysis(SLA)［C］.ASME MNHMT2009，2010，2:545－552.

［12］Schmandt B.，Herwig H.，Internal flow losses:a fresh look at old concepts［J］.Journal of Fluids Engineering－Transactions of the ASME，2011，133(5):051201－1－10.

［13］Herwig H.，Wenterodt T.，Second law analysis ofmomentum and heat transfer in unit operations［J］.International Journal of Heat and Mass Transfer，2011，54(7－8):1323－1330.

［14］Herwig H.，Kautz C..Technische Thermodynamik［M］.Pearson Studium，Muenchen，2007.

［15］Herwig H.，Gloss D.，Wenterodt T..A new approach to understand and model the influence ofwall roughness on friction factors for pipe and channel flows［J］.Journal of Fluid Mechanics，2008，613:35－53.