适于电磁场逆问题鲁棒和全局优化的蚁群算法研究

聂 曼， 杨仕友

(浙江大学电气工程学院， 浙江 杭州 310027)

1 引言

实际工程设计问题存在不可避免的不精确或不确定性。例如，由于加工误差，通常很难保证实际制造产品的尺寸与设计结果的一致性。因此，如果优化设计方案对于优化参数的微小变化非常敏感，则优化变量的轻微扰动可导致系统性能的严重退化，或违反约束函数导致无效解。因此，此时“最优”方案不再仅仅以目标函数作为评价标准，而需兼顾设计方案抗微小扰动(鲁棒性)的能力。从这个意义上讲，不确定性条件下电磁场逆问题鲁棒优化设计理论和技术成为计算电磁学的热点研究方向之一[1,2]。

所谓鲁棒性即指优化方案对决策变量或环境变量小扰动的不敏感性。现有文献通常采用均值和标准差作为目标函数和软约束函数的鲁棒性能参数，而简单地将“最坏解”作为强约束函数的鲁棒性能参数[3- 5]。因此，为计算某一具体可行解的鲁棒性，需要在其某一邻域内取大量采样点并计算这些采样点上的目标/约束函数值。这主要是因为实际逆问题中目标函数和约束函数没有解析解。换句话说，鲁棒优化算法的计算量远高于全局优化算法。至于目前鲁棒优化设计中所用的采样机制，一般为蒙特- 卡洛(Monte- Carlo)模拟法和其改进型[3,4]。尽管实现简便，但Monte- Carlo型的采样方法需要大量的采样点，因此这类方法计算效率较低。而电磁场逆问题的分析计算通常需要应用高精度的数值方法计算电磁场正问题，因此对计算资源来说无疑是雪上加霜。为降低计算成本，在不影响最优解质量的条件下，本文提出了电磁场逆问题鲁棒优化设计的快速蚁群优化算法(ACO)。

2 鲁棒优化蚁群算法 (ACO)

2.1 不确定条件下的鲁棒优化设计

一般工程设计问题中的不确定性可分为四类[5]。本文主要专注于电磁场逆问题中的第二类和第四类的不确定性，即产品的容差和加工精度的不确定性，以及可行性不确定性。对于涉及这些不确定性的逆问题，其数学模型可为：

(1)

式中，x是设计(决策)参数(变量)；δ是不确定性变量。

对于目标函数，本文采用平均或期望的适值函数衡量可行解x的鲁棒性能：

(2)

式中，p(δ)是不确定性或干扰的概率密度函数。

对于约束函数，采用两种不同的模型处理其鲁棒性，即采用最坏解策略搜索强约束条件的鲁棒解，定义为：

(3)

采用概率模型搜索软约束条件的鲁棒解，即第i个约束函数gi的概率模型为：

(4)

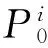
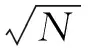
2.2 鲁棒优化蚁群算法

蚁群算法(ACO)是人们通过模拟没有任何智能的蚁群能够建立蚁穴至食物源最短路径过程而提出的一种启发式的搜索算法[7，8]。然而，这种算法搜索过程比较复杂，需要设计复杂的信息素更新机制。有鉴于此，人们通过研究墨西哥热带森林中的Pachycondyla Apicalis蚂蚁行为，提出了一种与Pachycondyla Apicalis 蚂蚁觅食策略相应的新蚁群算法，API算法(以Pachycondyla APIcalis命名)以解决优化问题[9]。

API算法将搜索过程划分为两个不同的搜索过程：全局搜索模拟蚁穴移动，局部搜索模拟觅食区域的搜索。因此，API算法的特有结构为开发快速鲁棒性能参数计算策略提供了可能。据此，本文提出了一种鲁棒优化API算法，其迭代过程如下：

(1) 初始化：设置算法参数；

(2) 生成新的蚁穴(全局搜索)：生成新的蚁穴N；

(3) 细化局部探索：

1) 强化搜索：对于每一个蚂蚁ai

如果ai在其记忆中有少于p个觅食区域，则在N的邻域创建一个新区域，并搜索这个新区域；

否则如果之前的区域搜索未成功，继续搜索同一区域；

否则搜索一个概率选择的区域(从记忆的p个区域中选择)；

2) 信息共享：用本搜索周期搜索到的最优区域概率地替换该蚂蚁记忆中的一个区域；

3) 蚁穴移动：如果满足蚁穴移动条件，则转向步骤4)；否则，转向步骤1);

4) 计算本搜索周期搜索到的最优解的鲁棒性能参数；

(4) 终止条件判断：如果条件成立，则停止搜索；否则，清空所有蚂蚁的记忆，然后转向步骤(2)。

2.3 鲁棒性能计算

约束优化问题的鲁棒最优解只能是局部/全局最优解，或者是位于约束条件边界上的解[10]。因此，优化过程中没有必要计算所有中间解的鲁棒性能参数。换句话说，对于一个理想的鲁棒优化算法应具有判断中间解性质，并只计算前述潜在鲁棒解的鲁棒性能参数的能力，以在保证解质量条件下最大程度地减少不必要的计算负担。而由本文前述的API算法的迭代过程可以看出，只有在搜索过程搜索到的最优解才有成为全局/局部最优解的可能。这个突出特点使得本文算法成为开发高效和简单鲁棒优化算法的理想选择，因为本文算法只需要计算上述潜在解的鲁棒性能即可以较小的计算代价搜索到优化问题的鲁棒最优解。据此，本文提出了API鲁棒优化算法鲁棒性能计算的简单策略，即在每次细化搜索后，只计算本次搜索阶段搜索到的最优解的鲁棒性能参数。很明显，只计算潜在解的鲁棒性能，而不是全部中间解的鲁棒性能，将大大减少优化算法的计算成本。而且，在同一细化搜索过程中大多数探索解都集中在当前蚁穴的附近，借助于本文设计的觅食区域生成机制，本文算法可以利用这些探索过的解，而不是像现有鲁棒优化算法那样再重新采样新点，计算潜在解的鲁棒性能参数。

为了在较少采样点条件下尽可能提高鲁棒性能指标的计算精度，本文又提出了利用多项式混沌近似构造目标函数响应面进而有效计算鲁棒性能参数的方法。

对于目标函数f(x,δ)，如果不确定变量δ遵循某一随机过程，它的有限阶P次多项式混沌近似为[11]：

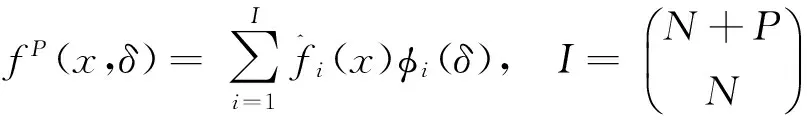
(5)

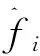
多项式混沌近似的突出优点是这些多项式基在某一内积规范下正交，即：

φi(δ)φj(δ)p(δ)dδ=δij

(6)

式中，δij是Kronecker 函数。

展开式系数为：

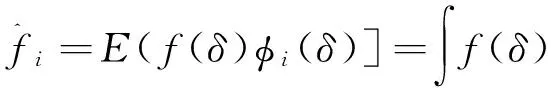
(7)

由多项式混沌近似式(5)，可以很容易地计算鲁棒性能指标：目标函数f(x,δ)的平均值和标准差。需要说明的是，如果采样点的个数为N，则多项式混沌近似的误差与eN成反比。因此，同样计算精度要求下，与现有的Monte- Carlo法相比，采用多项式混沌近似计算上述的鲁棒性能参数可明显降低采样点的数量。

2.4 兼具全局最优解和鲁棒最优解的搜索策略

现有鲁棒优化算法一般应用鲁棒性能参数评价解的好坏以指导搜索过程。由前述分析可见，只有局部最优解和边界解才有可能成为鲁棒最优解。因此，原始目标函数应该选为评价解的优良特性的驱动力。然而，如果单独使用目标函数为评价解的优良性的唯一依据就有可能搜索不到全局鲁棒最优解，这是因为中间解的鲁棒参数的信息没能用来指导搜索过程。为此，根据本文算法的结构特征，设计了一次搜索同时搜索鲁棒最优解和全局最优解的搜索机制。这种机制使用两种不同的标准评估解的质量。在搜索的内循环中，使用目标函数评价中间解；而在搜索的外循环中，则使用鲁棒性能参数评价、判断中间解。

3 计算实例

为验证本文提出的蚁群(ACO)算法的性能，将其应用于一个标准电磁场逆问题，Team Workshop Problem 22，即文献[12]所述的三个自由参数的超导磁储能(Superconducting Magnetic Energy Storage, SMES)系统优化设计问题。如图1所示，该储能系统包含两个同心线圈，内部主线圈和用于减少杂散磁场的外部屏蔽线圈。两个线圈中的电流方向彼此相反。SMES的设计需要满足：①系统中储存的能量为180MJ;②线圈内的磁场分布必须保证超导体不失超的特定物理条件;③沿着距离坐标轴10m的直线A和直线B上22个观测点的平均杂散磁场应尽可能的小。

为保证超导体的超导电性，两个线圈内的电流密度和磁通密度必须满足：

Ji≤(-6.4|(Bmax)i|+54)(A/mm2)i=1,2

(8)

式中,Ji和|Bmax|i分别是第i个线圈中的电流密度和最大磁通密度。

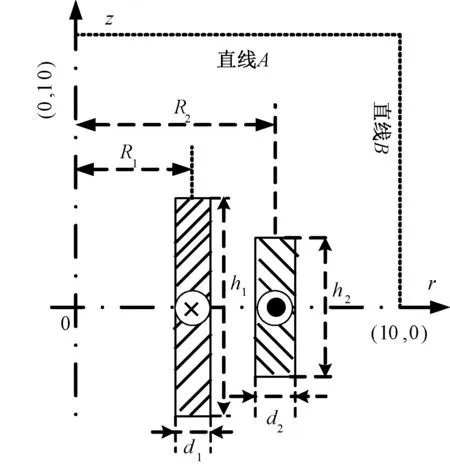
图1 SMES的结构示意图Fig.1 Schematic diagram of SMES

在三参数问题中，内部线圈固定，外部线圈的尺寸为优化变量。表1给出了这些参量的大小和变化范围。此外,线圈的电流密度都设定为22.5A/mm2。为方便数值计算，式(8)进一步简化为|Bmax|≤4.92T。在上述简化条件下，该优化问题可表示为

s.t. |Bmax|i≤4.92T

(9)

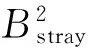
(10)

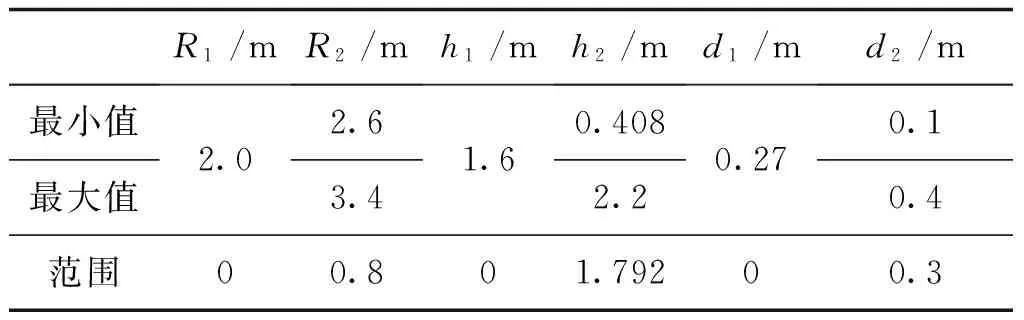
表1 问题22 参数值及其变化范围Tab.1 Details about parameters of team workshop problem 22

在优化过程中，式(9)和式(10)所需的性能参数通过二维有限元分析(FEA)确定。为进行性能比较，分别用本文蚁群(ACO)算法和一种鲁棒交叉熵(CE)法[10]求解该问题。在优化计算时，设优化变量存在某一不确定性的扰动，该扰动为1%的高斯随机扰动。经过2675次迭代搜索，本文算法在一次运行中搜索到了鲁棒解和全局最优解；搜索到的全局最优解非常接近国外参考文献给出的目前最优解[12]。与此相比，CE法需要3256次迭代才能找到相同的解。表2给出了这两种方法的最终优化解，以及国内外文献给出的目前最好解(IGTE)。需要指出的是表2中给出的IGTE的优化设计结果和原文献给出的设计结果略有不同，最主要是这里使用的剖分网格与原文略有不同。

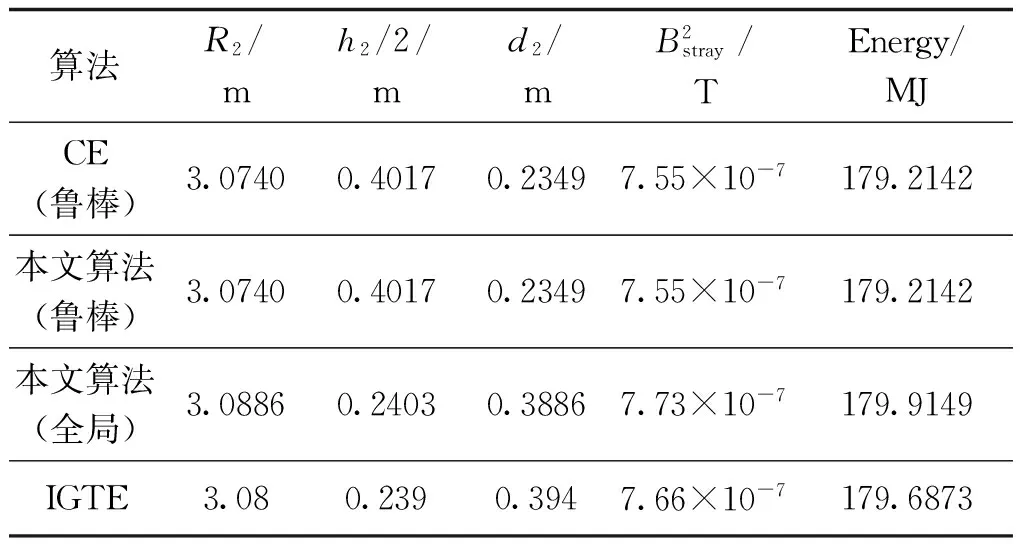
表2 不同优化算法的性能比较Tab.2 Performance comparisons of different algorithms on team workshop problem 22

由这些计算结果可见：

(1) 用目标函数值来衡量，全局最优解优于鲁棒最优解。具体结果是，鲁棒最优解对应的性能参数为：漏磁为7.55×10-7，储能为179.2142 MJ；而全局最优解对应的性能参数分别为：漏磁为7.73×10-7，储能为179.91 MJ；

(2) 然而，在优化参数上叠加1%的扰动后，鲁棒最优解对应的性能参数为：1.10605×10-6, 178.97250 MJ；全局最优解对应的性能参数为：1.40626×10-6, 183.28494 MJ。换句话说，本文算法获得到的鲁棒优化解的鲁棒性能比传统优化技术得的全局最优解的鲁棒性强壮得多；

(3) 本文算法的迭代次数大约是现有鲁棒CE方法迭代次数的82%；

(4) 本文提出算法的突出优点是它可以同时搜索到电磁场逆问题的鲁棒最优解和全局最优解。而且，本文算法搜索到的最优解的性能参数并不比目前国内外搜索到的最优解的性能参数差。

4 结论

典型算例的数值结果表明，本文提出的基于蚁群算法(ACO)的鲁棒优化算法主要特点是：① 在保证最终优化解准确性的前提下，可快速地搜索到鲁棒最优解；②可通过一次运行同时搜索到全局最优解和鲁棒最优解。因此，本文提出的鲁棒蚁群算法在逆问题的全局和鲁棒优化研究方面具有较强的竞争力。

[1] G L Soares, R L S Adriano, C A Maia,et al. Robust multi- objective TEAM 22 problem: a case study for uncertainties in design optimization[J]. IEEE Trans. Magn., 2009, 45(3): 1028- 1031.

[2] Nam- Kyung Kim, Dong- Hun Kim, Dong- Wook Kim,et al. Robust optimization utilizing the second- order design sensitivity information[J]. IEEE Trans. Magn., 2010, 46(8): 3117- 3120.

[3] J Branke. Evolutionary optimization in dynamic environments [M]. Norwell, MA: Kluwer, 2001.

[4] C K Goh, K C Tan, C Y Cheong,et al. An investigation on noise- induced features in robust evolutionary multi- objective optimization[J]. Expert System with Applications, 2010, 37(8): 5960- 5980.

[5] H G Beyer, B Sendhoff. Robust optimization- a comprehensive survey [J]. Comput. Methods Appl. Mech. Engrg., 2007, 196(33- 34): 3190- 3218.

[6] Marco Dorigo, Vittorio Maniezzo, Alberto Colorni. Ant system: optimization by a colony of cooperative agents [J]. IEEE Trans. System, Man, and Cybernetics- Part B: Cybernetics, 1996, 26(1): 29- 41.

[7] G Bilchev, I C Parmee. The ant colony metaphor for searching continuous design spaces [J]. Lecture Notes in Computer Science, 1995, 993: 25- 39.

[8] C Gagne, W L Price, M Gravel. Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence- dependent setup times [J]. Journal of the Operational Research Society, 2002, 53(8): 895- 906.

[9] N Monmarche, G Venturini, M Slimane. On how pachycondyla apicalis ants suggest a new search algorithm [J]. Future Generation Computer System, 2000, 16(8): 937- 946.

[10] S L Ho, Shiyou Yang, Yingying Yao，et al. Robust optimization using a methodology based on cross entropy methods [J]. IEEE Trans. Magn., 2011, 47(5): 1286- 1289.

[11] D Xiu, G Karniadakis. The Wiener- Askey polynomial chaos for stochastic differential equations [J]. SIAM J. Sci. Comput., 2002, 24(2): 619- 644.

(，cont.onp.70)(，cont.fromp.47)

[12] TEAM optimization benchmark problem 22 [OL].http://www.igte.tugraz.at/team22/.