优化的混合核函数相关向量机在发酵过程建模中的应用
2014-03-27余荣荣周家旺
余荣荣,周家旺
(1.安徽师范大学 数学计算机科学学院,安徽 芜湖 241000;2.武汉理工大学 机电工程学院,湖北 武汉 430070)
微生物发酵过程复杂,一些重要的参数如产物浓度、菌体浓度不能实时测量得到.近年来,通过软测量技术,发酵过程模型的预测精度越来越高.刘毅等[1]利用最小二乘支持向量机(LSSVM)与Pensim仿真平台建立了青霉素产物浓度等重要过程变量的在线预测模型.相关向量机(RVM)是基于支持向量机的概率模型,采用概率式的预测结果,在贝叶斯框架下用于数据分类与预测[2].支持向量机在解决高维、非线性和小样本问题时具有良好性能[3],而相关向量机与支持向量机相比,具有更稀疏的结构和更少的相关向量,且核函数选择不局限于Mercer条件等优点[4].
本文将高斯核函数与Sigmoid函数采用加权的方式形成混合核函数应用于RVM,并采用差分进化算法对混合核函数相关向量机的参数进行优化.对青霉素发酵过程产物浓度进行预测,并与2种单一核函数的相关向量机建模结果进行比较,仿真表明该混合核函数模型具有较高的预测精度.
1 相关向量机
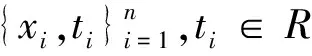
ti=y(xi,ω)+εi.
(1)
与SVM类似,RVM将回归函数表示成核函数K(x,xi)的线性组合形式,即
(2)
其中ω=[ω0,ω1,…,ωN]T是模型的权值向量,ω0为回归函数的偏置.

(3)
基于训练数据的独立性,引入超参数β=1/σ2,整个训练数据集的似然函数为
(4)
其中t=[t1,t2,…,tN]T,φ是核函数对输入xi的响应:
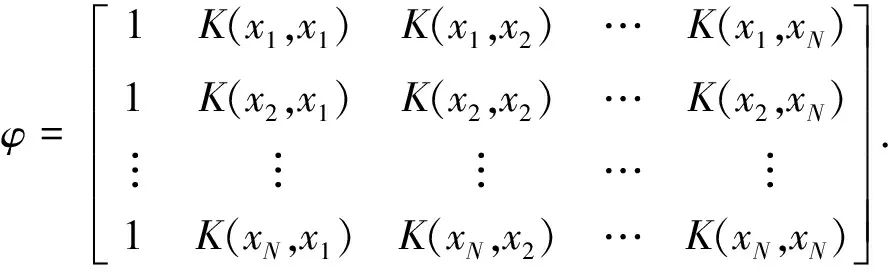
(5)
式(3)中α=[α0,α1,…,αN]T,每个独立的超参数αi只与其对应的权值ωi相关,根据先验分布和似然函数,利用贝叶斯公式计算权值的后验分布,即
(6)
式(6)中,p(ω|α)和p(t|ω,β)均满足高斯分布,因此其乘积p(ω|α)p(t|ω,β)也满足高斯分布,而p(t|α,β)不含参数ω,可看作归一化参数,所以权值的ω后验分布可表示为:
p(ω|t,α,β)=N(μ,Σ) .
(7)
上式中,协方差Σ=(βφTφ+A)-1,均值μ=βΣφTt,其中A为对角阵,A=diag{α0,α1,…,αN}.
为获取ω的最大后验分布,最大化边缘似然函数p(ω|t,α,β)取负对数得到目标函数,最后令目标函数分别对超参数αi和β求偏导得到优化的超参数:
(8)
(9)
式中,μi为权值后验均值向量μ的第i个元素,Σi,i为协方差阵Σ的第i个对角元素,γi=1-αiΣi,i.在RVM训练中,式(8)和(9)需要依次迭代,直到参数αi和β收敛.将迭代后的最终参数代入式(2)中得到训练数据的回归模型.
2 多核相关向量机及参数优化
对于相关向量机,其核函数的构造和选择对于模型预测精度影响很大.相关向量机只使用单核函数会造成性能单一且局限性较强.Gauss核函数是典型的局部核函数,Sigmoid核函数是具有全局特性的全局核函数,结合二者可以同时提升学习能力和泛化能力.
采取下面的混合方式组成新的混合和函数:
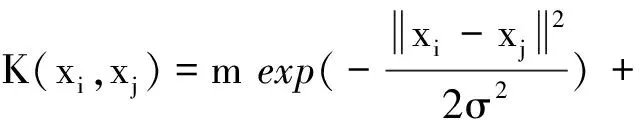
(10)
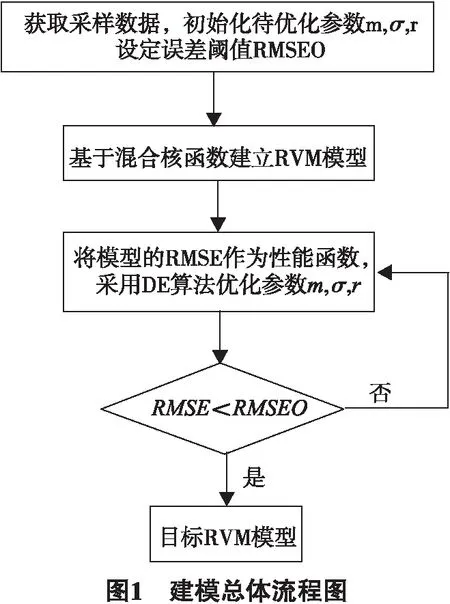
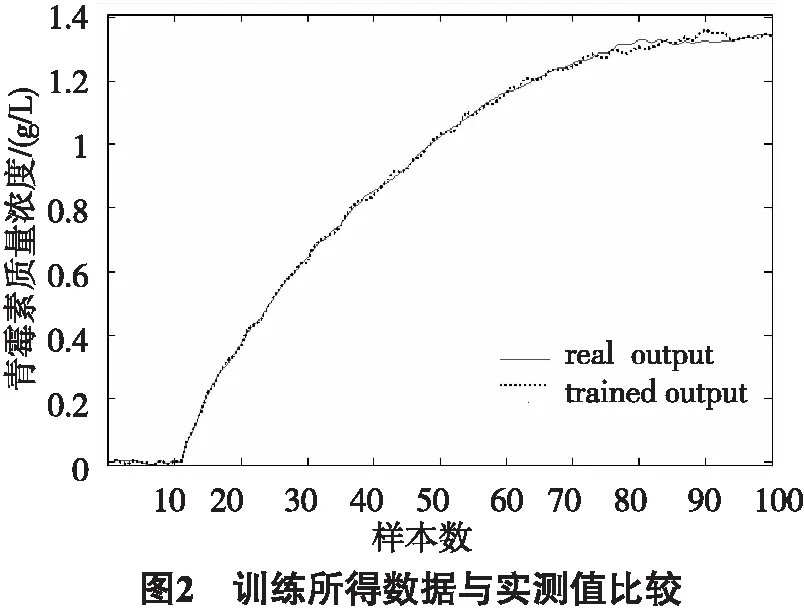
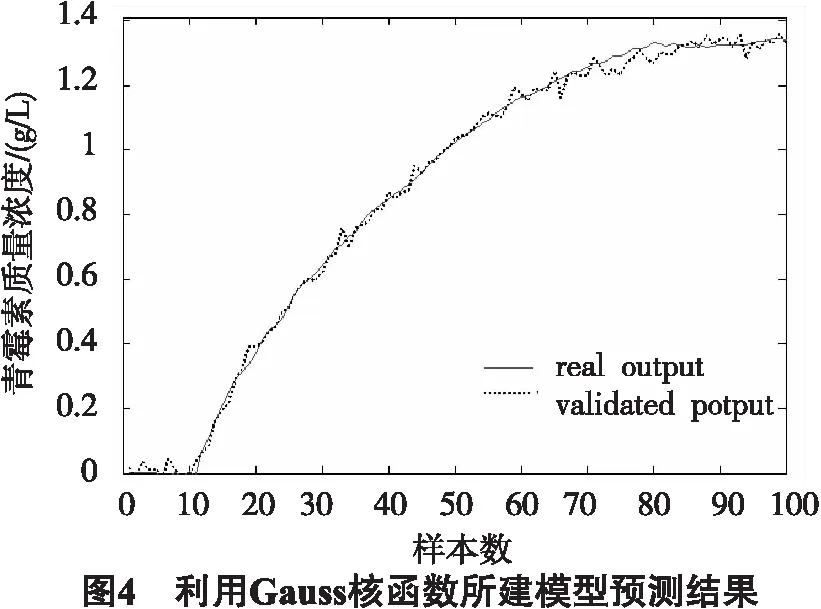
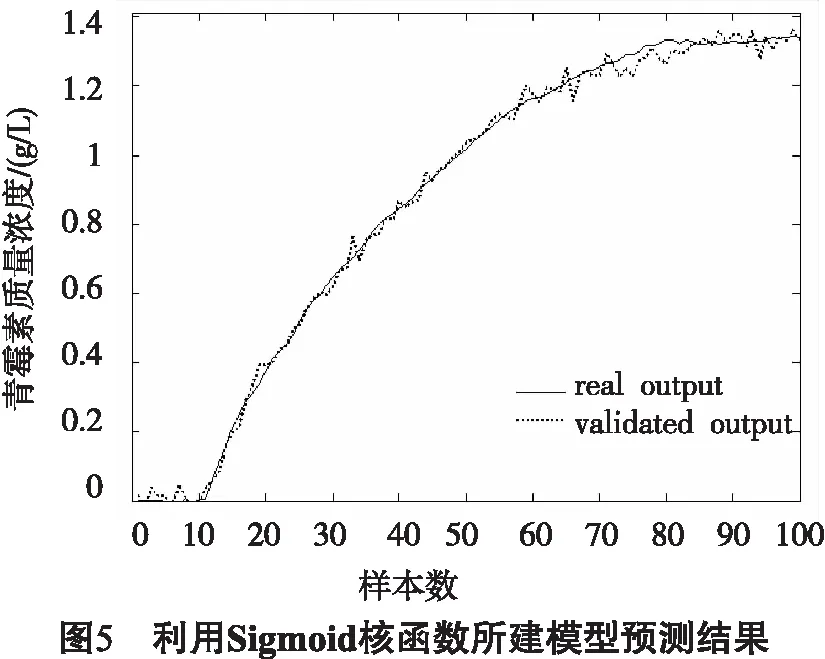
其中,m是调节系数,且0 差分进化(DE)算法[7-8]是一种生物启发式全局搜索算法,和遗传算法类似,每代迭代过程中保留最优解.采用DE算法进行参数寻优,其具体步骤包括:首先根据待优化参数的维数种群大小NP,随机生成参数向量作为初始种群: (11) (12) 青霉素发酵中具有时变性、高度非线性等特征,系统采集的数据有噪声干扰,有损建模精度,需要选取合适的建模方法,才能有效提高模型的预测精度[9].Pensim仿真平台基于发酵的机理模型,考虑了关键变量对发酵过程产生的影响,能模拟包括青霉素产量、温度、溶解氧量等关键变量[10]. 基于Pensim仿真平台进行某些初始条件的设定,并在正常情况下产生数据.在这些数据中选取100组作为RVM的训练样本,同时也选定用于预测的数据.将混合核函数用于RVM建模过程,提高模型拟合精度,同时采用差分进化优化算法对建模过程参数进行优化,找到全局最优解.具体建模过程如图1所示. 图2显示了利用所得数据建立的发酵过程模型,图3为模型的预测结果,其表明混合核函数相关向量机能较高精度地预测青霉素浓度,可用于发酵过程实时控制.为比较混合核函数的优越性,分别给出了Gauss核函数和Sigmoid核函数分别用于RVM的建模结果,如图4、5所示.对比图3~5和性能指标(表1),可以看出,混合核函数模型比单一核函数模型具有更高的预测性能与泛化能力. 表1 青霉素浓度预测误差比较 本文采用Gauss核函数和sigmoid核函数结合形成的混合核函数应用于相关向量机的建模,并基于差分进化算法对其参数进行优化,建立青霉素发酵过程模型,仿真实验表明了该算法用于青霉素发酵过程建模的有效性.本文进一步比较了混合核函数模型与单一核函数模型的预测误差结果,表明混合核函数相关向量机有强抗扰能力和令人满意的预测精度.在线优化建模参数并将混合核函数相关向量机应用于具体样机是下一步需要研究的内容. 参考文献: [1] 刘毅,王海清.采用最小二乘支持向量机的青霉素发酵过程建模研究[J].生物工程学报, 2006,22 (1):144-149. [2] TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].The Journal of Machine Learning Research, 2001(1):211-244. [3] 谷雨.基于支持向量机与移动 Agent 的入侵检测系统模型[J].云南民族大学学报:自然科学版, 2008, 17(1): 68-71. [4] 李刚,邢书宝,薛惠锋.基于RBF核的SVM及RVM模式分析性能比较[J].计算机应用研究,2009,26(5): 1782-1784. [5] 朱世增,党选举.基于相关向量机的非线性动态系统辨识[J].计算机仿真, 2008, 25(6):103-107. [6] 朱永利, 尹金良.组合核相关向量机在电力变压器故障诊断中的应用研究[J].中国电机工程学报, 2013, 33(22): 68-74. [7] 熊伟丽, 许文强, 赵兢兢, 等.运用ADE算法进行Wiener模型辨识[J].系统仿真学报, 2013, 25(005): 969-974. [8] 姜立强, 刘光斌, 郭铮.基于差分进化算法的 PID 参数整定[J].计算机仿真, 2009 (6): 204-206. [9] HONG Jeong-jin,ZHANG Jie.Quality prediction for a fed-batch fermentation process using multi-block PLS[J].Springer Proceeding in Physics, 2010, 135:155-162. [10] 熊伟丽, 王肖, 陈敏芳, 等.基于加权 LS-SVM 的青霉素发酵过程建模[J].化工学报, 2012, 63(9): 2913-2919.
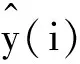
3 发酵过程建模


4 结语
