价格波动网络传播模型：研究价格波动关联效应的新方法*

刘向荣，杨建梅，孙红英，谢伟聪，蓝文妍

(1.华南理工大学工商管理学院 ，广东 广州 510640；2.仲恺农业工程学院计算科学学院, 广东 广州 510225；3.中山大学管理学院, 广东 广州 510275)

价格波动关联效应一般是指商品价格之间存在的互相作用、相互推动的影响，可简述为当一种或数种商品价格出现变化，因因果互动关系，其将影响到多少种商品价格发生波动，影响幅度有多大[1-2]。近年来，学者们纷纷利用经济计量、一般均衡、投入产出价格影响等模型或者它们相结合的方法研究商品价格波动对其它商品的关联影响[3-9]。张红霞[7]把传统价格影响模型的初始假设约束进一步放松，引入市场供求关系及政府调控等因素，解决了以往运用价格影响模型研究无法充分反映市场供求和政府价格管制等因素对价格波动影响的不足。韩一杰等[8]引入了政府价格管制、价格滞后影响、需求度等三个影响价格运行的变量，对投入产出价格影响模型进行了新改进，建立了新的反映市场供求和政府管制条件下的价格影响模型，分析了中国猪肉价格波动可能对CPI中8大类价格指数的影响程度，进而对总体CPI 的影响。廖明球等[9]将投入产出模型与计量经济模型结合起来，建立了综合模型研究一部分产品价格变动对另一部分产品价格变化的影响，分析产品价格变动可能对综合价格指数的影响。

由于上述运用投入产出价格影响模型研究价格波动关联效应存在拆并投入产出表困难，导致研究推广非常困难。如要拆分出某种商品，就要了解该商品在农业部门中的产值和比重，才能拆并出符合研究要求的投入产出表。一方面这方面数据难以搜集；另一方面由于统计的分类、分目的原因，很难细分到具体商品(每个品种)。需要探索更为简单有效的方法来研究价格波动关联效应，为价格宏观管理部门提供简易可行的测算工具和方法。自1998年Watts和Strogatz引入小世界(Small-World)网络模型[10]，1999年Barabasi和Albert引入无标度(Scale-Free)网络以来[11]，关于复杂网络的研究方兴未艾，学者们分别基于规则网络、随机网络、小世界网络和无标度网络，建立了相应的网络传播模型，运用网络传播开展了动力学机制、社会舆情传播、病毒传播、价格波动等研究[12-16]，但运用网络传播方法来研究价格波动关联效应还比较少见。

在文献[8]研究的基础上，从经济学中常用于研究价格波动关联效应的模型——基于投入产出理论的价格影响模型出发，以2007年广东省价值型投入产出表为基础[17]，对照CPI总指数包含的8大类指数，建立了30个部门(或商品)投入产出表，构建了广东价格波动影响模型，测算了30个部门价格波动关联效应。并将该关联效应投射到网络上，运用网络表达了价格影响模型下价格波动关联效应。在此基础上，引入网络传播视角，将价格波动关联效应视为网络节点之间的传播行为，构建网络价格传播模型模拟了上述关联效应，并运用该模型研究了240种消费品价格波动关联效应。模型可为测算消费品价格波动之间的相互影响，研究消费品价格波动与CPI(居民消费价格总指数)之间的相关关系，进而推测CPI运行走势提供新的途径。

1 构建广东价格影响模型

1.1 数据来源

以广东省统计局公布的2007年广东省135个部门投入产出表[17]，对照纳入CPI统计的8大类商品和服务价格，通过拆并的方式，拆分出来包含30个部门(或商品)的投入产出表[1]。

1.2 建立改进的广东价格影响模型

新建立的价格影响模型的假设和部分参数φj、φj、f(x)的设定(这里φj为供求关系与政府调控联合影响函数，φj表示投入产出表中第j部门税率与利润率之和，f(x)表示滞后影响函数)，遵从文献[8]模型的假设和参数设置方法。并引入金融财务管理中的贝塔系数(β)、传导率(γ)以及对外敏感度(θ)3个参数来表示市场供求、价格传导、经济外向度等因素，对参考文献[8]模型直接和间接影响推动公式进行了新的改进，建立了市场供求关系变化和开放条件下广东价格影响模型。

此处价格波动贝塔系数(β)定义为某种商品价格上涨相对于整体价格总水平(即基准水平)的弹性，如β>1，则表示该种商品可能供求不平衡，拉动价格总水平上涨。为简化研究，这里用2010年上述30个部门(或商品)对应的价格指数除以广东CPI指数，对于部分部门(或商品)无对应指数则采用相近指数替代(下同)；传导率定义(γ)定义为上游商品价格上涨引发下游商品价格上升的传导效应，如γ>1,表示市场商品供不应求，上下游产品价格传导顺畅，反之亦然。同样用2010年上述30个部门(或商品)广东CPI指数除以对应PPI价格指数；对外敏感度(θ)表示某种商品价格受国际市场价格影响的程度，如θ>1，则表示商品价格对国际市场敏感，反之亦然。为简化，这里根据对外依存度与广东市场相应30个部门(或商品)价格指数相关系数取值情况，将对外敏感度(θ)值分别设定为1.1和0.9[1]。

当第i部门涨价Δpi时，其涨价t个单位时间后对第j部门产品价格的直接推动[8]，

(1)

修改为

(2)

当第i部门产品涨价t个单位时间后通过第r部门产品对第j部门涨价的一次间接推动[8]

(3)

相应修改为

(4)

同理第i部门涨价t个时间后，经过直接推动和n-1 次间接推动后，第j部门产品价格受到的总推动[8]，

f(Tr+Ts+Tj)+…,1≤k≤n-1

(5)

相应修改为：

f(Tr+Ts+Tj)+…,1≤k≤n-1

(6)

1.3 测算价格波动关联效应

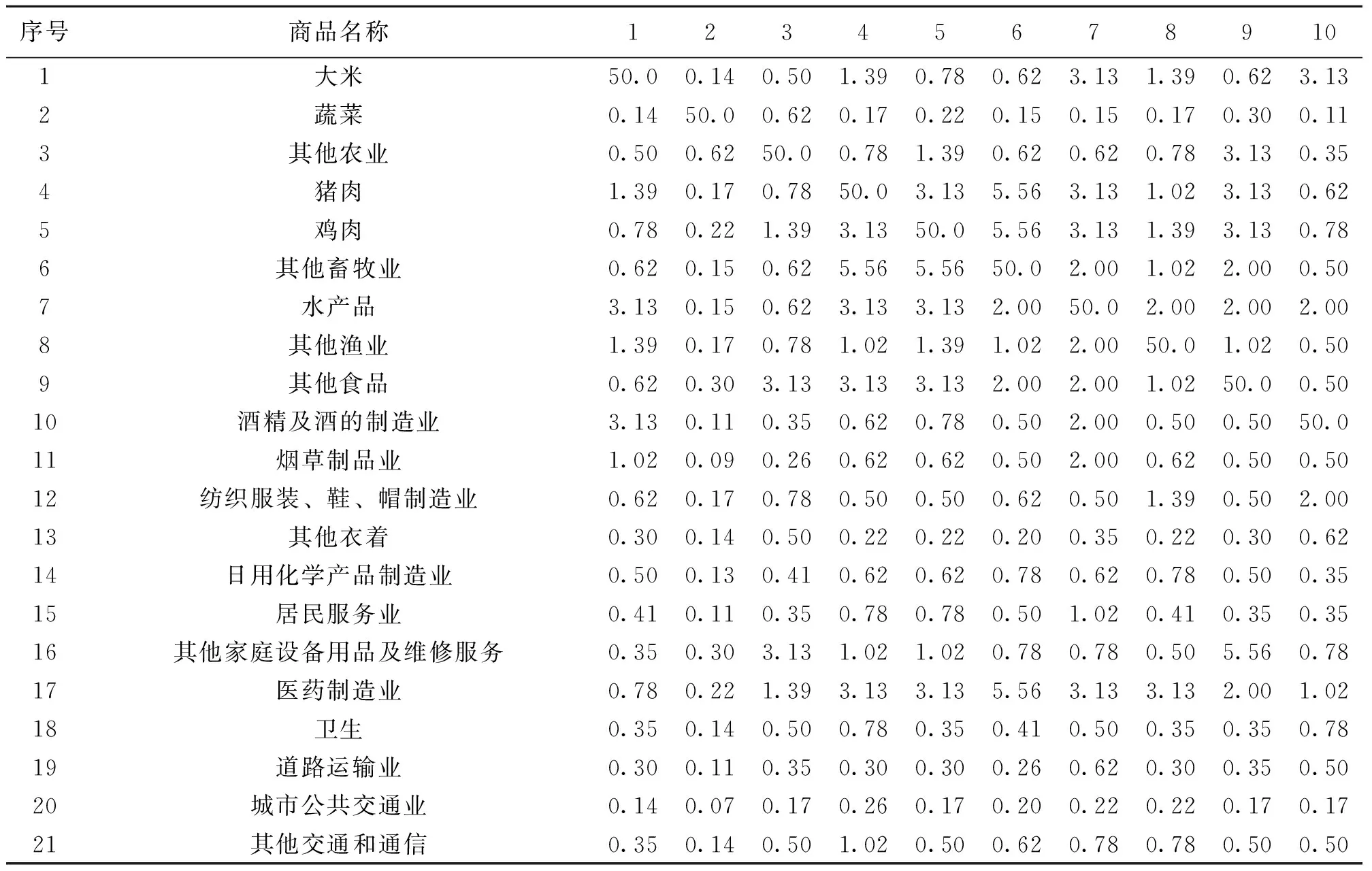
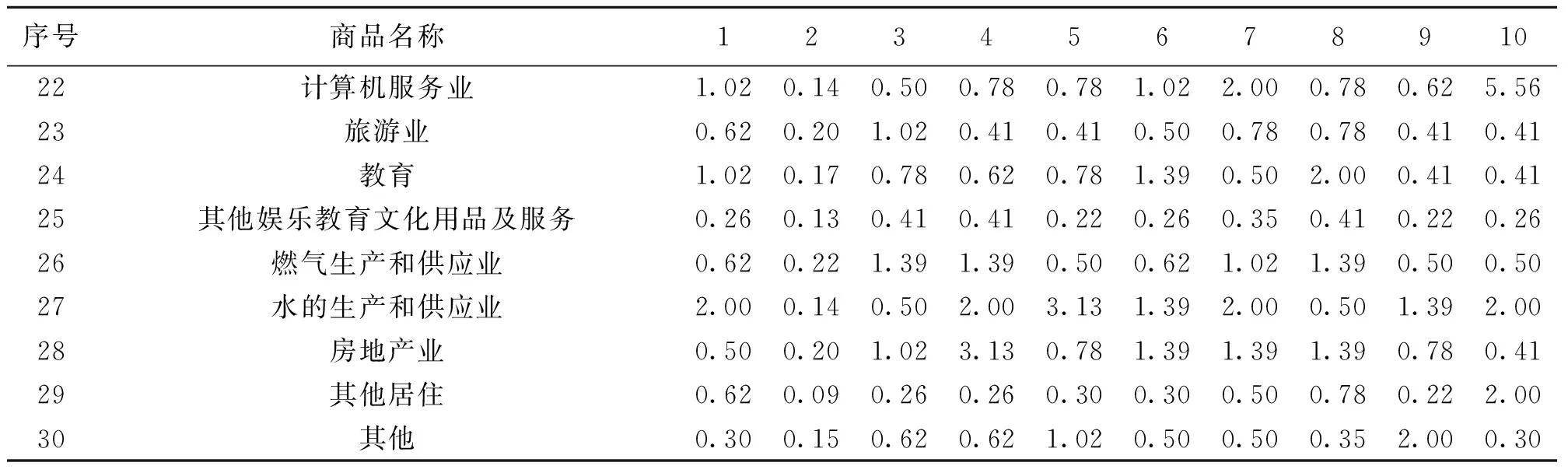
为研究方便，假设上述30个部门(或商品)价格依次上涨50%(即Δpi=50%，i=1,2,…,30)，计算其波及其余部门数目和幅度，阈值(ρ)设定为1%(见表1)。测算表明，其它部门、其它农业、蔬菜、其他娱乐教育文化用品及服务、其他交通和通信、其他食品、其它居住对其余部门价格波动的影响面比较广，分别波及了22、11、10、9、8、8、8个部门。如蔬菜，其价格变化波及了10个部门，说明其对其余部门价格上涨的影响力比较大，需要在CPI调控时作为重点商品加以监控，综合做好蔬菜调储工作。

从各部门(或商品)价格上涨分别影响其他部门价格上升幅度来看，当大米价格上涨50%，其拉动蔬菜价格上涨0.55%，鸡肉和其他畜牧业价格上涨0.66%，其他农业、猪肉价格上涨0.55%、0.53%；蔬菜价格上涨50%，则拉动大米、其他农业、猪肉和其他畜牧业价格上涨1.4～2.1%，带动其他食品、酒精及酒的制造业价格上涨3.95%和3.37%；鸡肉价格上升50%，影响猪肉、其他畜牧业价格分别上涨0.51%和0.63%；水产品价格上涨50%，将影响其他食品上涨1.16%；房地产业价格上涨50%，则拉动道路运输业、其他家庭设备用品维修服务价格分别上涨0.41%，城市公共交通业价格上涨0.5%，说明房地产业价格上涨波及面比较广，影响面大。

2 运用网络表达价格波动关联效应

将上述30个部门(或商品)作为网络的节点，分别按照序号进行编号(i=1,2,…, 30)，以上述测算的价格波动关联效应为边权(见表1)，建立完全网络M0。由于前述30个部门(或商品)之间价格波动关联关系是双向互动关系，故该网络为有向加权网络，即网络有出度和入度之分，并且出度和入度权值不对等。

为掌握在不同阈值条件下，网络拓扑性质的差异，设定两个阈值ρ=1%或0.5%(这里ρ为前述测算的30个部门或商品之间的价格波动关联效应，见表1)，当a(i,j)<1% 或a(i,j)<0.5%，节点i和节点j之间不连边，反之则连边，建立两个有向网络M1(见图1)和M2(见图2)(以下简称投射网络M1和M2)，为简述，下面只介绍网络M2价格波动关联情况。

图1 投射网络M1拓扑图[1]Fig.1 The topology figure of projection networkM1

序号商品名称123456789101大米50.01.401.780.130.070.170.010.010.350.002蔬菜0.5550.02.230.170.080.210.010.010.440.003其他农业0.551.7550.00.170.080.210.010.010.440.004猪肉0.531.682.1450.00.511.300.020.031.160.015鸡肉0.662.102.671.2750.01.620.030.041.460.016其他畜牧业0.662.102.671.270.6350.00.030.041.460.017水产品0.321.021.300.110.050.1450.00.062.210.028其他渔业0.321.021.300.110.050.140.0550.02.210.029其他食品1.243.955.032.501.243.181.161.4050.00.4410酒精及酒的制造业1.053.374.300.290.140.370.130.168.0350.011烟草制品业1.193.814.850.030.020.040.000.010.270.0012纺织服装、鞋、帽制造业0.000.010.010.010.000.010.000.000.210.0013其他衣着0.090.290.381.070.531.360.010.010.500.0014日用化学产品制造业0.000.000.000.000.000.000.000.001.540.0115居民服务业0.461.501.930.000.000.000.000.001.560.0016其他家庭设备用品及维修服务0.000.000.000.000.000.000.000.000.500.0117医药制造业0.220.700.890.060.030.070.020.020.900.1518卫生0.000.000.000.000.000.000.000.000.030.0019道路运输业0.000.010.010.010.000.010.000.000.190.0020城市公共交通业0.000.000.010.000.000.000.000.000.100.0021其他交通和通信0.000.010.010.000.000.010.000.000.130.0122计算机服务业0.000.000.000.000.000.000.000.000.000.0023旅游业0.000.000.000.000.000.000.000.000.000.0024教育0.000.000.000.000.000.000.000.000.000.0025其他娱乐教育文化用品及服务0.000.000.000.000.000.000.000.000.000.0026燃气生产和供应业0.000.000.000.000.000.000.000.000.000.0027水的生产和供应业0.000.000.000.000.000.000.000.000.000.0028房地产业0.000.000.000.000.000.000.000.000.000.0029其他居住0.000.000.000.000.000.000.000.000.000.0030其他0.030.110.140.000.000.010.020.020.340.00

1)因页面所限，表格进行删节

图2 投射网络M2拓扑图[1]Fig.2 The topology figure of projection network M2

投射网络M2节点的出度值，是指该网络节点(部门或商品)价格上涨将会引起其余多少个节点(部门或商品)价格上涨超过0.5%。由图2可知，投射网络M2中节点最小的出度值为0，这些节点共有10个，其编号分别为7、10、11、12、15、18、20、23、24、26，表示当这些节点的价格上涨50%时，基本不波及到其他部门(或商品)，对应到30个具体部门(或商品)来看，当水产品、酒精及酒的制造业、烟草制品业、纺织服装鞋帽制造业、居民服务业、卫生、城市公共交通业、旅游业、教育、燃气生产和供应业依次上涨50%，推动其余29种商品价格上涨不超过0.5%，可称为惰性部门(或商品)。与投射网络M1对比，惰性部门(或商品)增加了水产品、烟草制品业、燃气生产和供应业3个部门。节点的最大出度值为29，这类节点共有4个，其编号分别为21、25、29、30，具体到部门(或商品)分别是其他交通和通信、其他娱乐教育文化用品及服务、其他居住、其他部门等4个部门(或商品)，说明当这些节点的价格上涨50%时，其它29种商品全部会受到其波及，且上涨幅度在0.5%以上，这些部门是活跃部门(或商品)。与投射网络M1对比，发现活跃部门(或商品)没有变化。从具体部门(或商品)来看，猪肉价格上涨会波及4个部门，房地产业波及14个部门，蔬菜和其他农业分别波及12和13个部门，这些商品价格变化对其余商品价格上涨将产生波及效应，这一结论与前几年因上述商品价格大幅度上涨导致CPI随之快速上升现象基本吻合，说明将价格影响模型下价格波动关联效应投射到网络上，并没有出现失真现象，与现实价格波动影响结果基本一致，也可说明运用网络来反映价格波动关联效应是可行的。

投射网络M2节点入度，是指该节点所代表的部门(或商品)将会受到其余多少个部门(或商品)价格波及的影响而随之上涨。网络中节点最小的入度值为4，有3个节点，这些节点编号为20、26、28，具体到部门(或商品)就是城市公共交通业、燃气生产和供应业、房地产业，较投射网络M1增加了2个部门(或商品)，说明这3个部门受别的部门价格波动的影响很小，在30个部门(或商品)中具有较强的独立性，不容易受到其他部门(或商品)的影响而上涨。网络中节点最大入度值为12，只有1个节点，该节点编号为9，也是其他食品，较投射网络M1没有变化，表明其余商品价格上涨50%，都对其他食品部门影响幅度均超过0.5%，从病毒传播概念来说其他食品部门属于易感染人群。节点入度值在5～8的有22个，占据节点总入度数的73.3%。其中入度值为6、7、8的节点有5个，分别占30个节点总入度数的50%；入度值为5和4的节点，分别有7、3个节点，分别占节点总数的23%和10%。

3 构建网络传播机制模拟价格波动关联效应

前面，将价格影响模型下的价格波动关联效应投射到网络上，通过网络节点之间的连边关系和边权可清楚地反映商品之间价格波动关联效应。构建网络传播机制模拟上述用网络表达的价格波动关联效应，一方面要构建一个新的网络反映投射网络M2节点之间的连边关系(模拟网络)，另一方面要探索出反映网络M2边权的(为简化，这里只研究出度边权)传播方程。也就是说运用网络传播模拟价格波动关联效应，既与用来模拟的网络本身结构有关，同时与用来模拟的传播方程有关。具体涉及到两个变量：第一，网络拓扑结构变量。在上述网络投射研究中，发现在建立网络时，可通过设立阈值来控制网络拓扑结构，即网络的拓扑结构与选择的阈值密切相关，是阈值的函数，阈值是自变量，网络拓扑结构是因变量。为简化研究，这里通过控制阈值来控制网络拓扑结构。第二，传播动力学方程。探索出适合的传播方程对模拟有效非常关键。

3.1 构建价格波动模拟网络

1)模拟数据来源。对应上述30种产品和部门，从纳入广东省CPI统计的商品或部门价格指数中，分别找出上述30种商品(或部门)相对应的价格指数，部分商品没有对应的价格指数，采取相近或者相类似的价格指数替代。给上述每种商品(或部门)分别从1-30编号，取2001年1月至2012年4月上述30种商品或部门每月同比价格指数作为时间序列，分别用A1,A2,…,A30表示，

A1=(a11,a12,…,a1,12),A2=(a21,a22,…，a2,12),…,A30=(a30,1,a30,2,…，a30,12)，其中，aij(i=1,2,…,30，j=1, 2,…,12)代表当月的同比价格指数[1]。

2)计算相关系数矩阵。以上述30种商品(或部门)作为网络的节点，将上述商品同比价格指数时间序列两两求相关系数(见公式4)，以相关系数ρ作为边权表示两种商品之间价格波动相关性大小(即此种商品上涨拉动彼种商品上涨的能力),得到相关系数矩阵。

-1≤ρij≤1

(7)

(ai表示第i种商品每月价格指数序列，aj表示第j商品每月价格指数序列，且i≠j，表示每月价格指数序列的平均值。)这里，利用maltlab里自带的函数corrcoef即可方便计算出这30种商品的相关系数矩阵R，这是一个对称矩阵，其中自相关系数为1，上述相关系数有正负数[1]。

3)计算上述相关系数矩阵平均值。对上述30种商品相关系数矩阵R的元素取绝对值，并计算出相关系数矩阵的平均值r_mean。

4)建立价格波动关联网络Mj。相关系数矩阵R中元素r(i,j)，如r(i,j)≥r_mean，则令:network(i,j)=round(10*r_mean / r(i,j))，round目的是取四舍五入的数值，这里乘以10是指把边权的最大值设为10，由于r_mean约为0.2，理论边权最小值为2。如r(i,j)

3.2 探寻网络传播方程

要使得通过网络传播来模拟前述运用网络M2表达价格影响模型下的价格波动关联效应，需要同时控制上述两个变量。为解决这一难题，采取先固定一个变量不变(传播方程)，不断调整修正另一个变量(网络阈值)，使得通过网络价格传播来模拟前述价格波动关联效应规律尽可能一致[1]。

1)构建网络价格传播动力学方程。根据以往网络传播规律的研究，网络的传播一般是通过网络的最短路径按照某种规律来传播，并且随着传播路径的延长，传播影响或者能力将依据某种规则快速衰减，也就是网络传播的影响力与距离应呈某种反比关系。这里，首先分析网络M3的最短路矩阵，在假设商品i上涨Δpi，如商品j的价格上涨幅度简单地与距离成反比关系，即：Δpj=Δpi/distance(i,j)，(这里Δpi与前述同样取50%,i=1,2,…,30)，则商品j的价格受波及情况与网络M2差异较大。如采用Δpj=50%/distance(i,j)2传播机制，初步测算发现商品j的价格上涨幅度数量级和幅度与网络M2权值(出度值)吻合度较高。为此，采用该传播方程作为网络模拟的传播机制。

2)调整和修正价格波动关联网络阈值。为了使得通过网络传播模拟的价格波动效应更加符合在价格影响模型下价格波动的实际状况，达到在网络上商品价格上涨波及的商品数目与价格影响模型下商品波及的商品数目(M2)基本接近，并且影响幅度也大致符合。按照上述传播方程：Δpj=50%/distance(i,j)2，在0≤P≤0.01区间内反复试验，不断调整和修正前面所建网络M3的阈值(相应改变网络的拓扑结构)，表明当阀值设为P=0.007时，通过网络价格传播模拟的价格波动关联效应与实际状况(M2)比较接近，在网络价格传播模拟下受到波及的部门或商品总数为286个，与M2表达的价格影响模型下价格受到波及的部门或商品总数285个大致相近，波动幅度也比较接近。

3.3 运用网络价格传播模型测算价格波动关联效应

下面，在阀值P=0.007时建立的网络，按照商品价格波动沿网络最短路并按照传播方程：Δpj=50%/distance(i,j)2快速传播方式，计算每种产品依次上涨50%，对其余部门或商品的影响幅度(见表2)。

表2 网络传播模型下价格波动关联效应1)Table 2 The associated effects on price volatility based on network spread %

续上表

序号商品名称1234567891022计算机服务业1.020.140.500.780.781.022.000.780.625.5623旅游业0.620.201.020.410.410.500.780.780.410.4124教育1.020.170.780.620.781.390.502.000.410.4125其他娱乐教育文化用品及服务0.260.130.410.410.220.260.350.410.220.2626燃气生产和供应业0.620.221.391.390.500.621.021.390.500.5027水的生产和供应业2.000.140.502.003.131.392.000.501.392.0028房地产业0.500.201.023.130.781.391.391.390.780.4129其他居住0.620.090.260.260.300.300.500.780.222.0030其他0.300.150.620.621.020.500.500.352.000.30

1)因页面所限制，其余部门删节

从表2可见，在大米价格上涨50%情况下，也同样会拉动酒精及酒的制造业和猪肉价格分别上涨3.13%、1.39%，这个结果与价格影响模型下结果大致一致，这可能与酿酒行业和猪肉生产行业直接以大米为原料较多，受大米价格波动影响较大的缘故。同样如阈值ρ设定为1%，发现食品行业、医药制造、燃气生产和供应业、计算机服务业、房地产业波及范围较广，均波及10个以上部门，这点与以前研究和居民消费日常感受比较一致，也与在价格影响模型下的结论大致相同，由此说明运用网络传播来模拟价格波动关联效应是比较可行的途径。其中水产品、猪肉、鸡肉、其他渔业、其他畜牧业、其他食品等食品行业分别波及14、12、11、10、10个部门，特别是猪肉价格上涨50%情况下，相应带动鸡肉、其他畜牧业、水产品、其他渔业、其他食品3.13、5.56、3.13、1.02、3.13个百分点，更加说明这些食品是容易引起其它部门价格上涨的源头商品，需要特别予以供应保障和价格监测预警。

3.4 网络价格传播模型与价格影响模型下的价格波动关联效应差异分析

通过网络价格传播模拟价格波动关联效应与价格影响模型下价格波动关联效应对比，从价格波动关联关系差异看，发现价格波动网络传播模拟的价格波动关联关系与价格影响模型下价格波动关联关系整体绝对误差率为48%，误差率不超过50%的商品部门为17个，说明运用价格波动网络传播模型模拟价格影响模型下的价格波动关联关系，模拟的准确率高于50%，具有一定的应用价值。从具体部门(或商品)来看，6、10、12、24号部门(或商品)分别对应其他畜牧业、酒精及酒的制造业、纺织服装鞋帽制造业、教育，模拟绝对误差率低于10%，占总部门(或商品)的13.3%，这些部门(或商品)在上述两个模型中对其余部门(或商品)影响的数目差异不大，比较接近。从价格波动关联效应模拟幅度差异看，发现平均误差处于0.22～8.38，总平均误差为1.06个百分点。其中介于1.03～1.46有9个部门(或商品)；0.22～0.97有20个部门(或商品)，说明在两个模型下，绝大多数部门(或商品)价格波动关联影响幅度差异低于1个百分点，模拟吻合度相对比较高。

4 价格波动网络传播模型初步推广运用

下面，运用价格波动关联效应网络传播机制(即在阈值P=0.007时建立的价格波动关联网络，按照商品价格波动沿网络最短路及传播方程：Δpj=50%/distance(i,j)2快速传播)，测算240种消费品价格波动关联效应情况，为研究大样本价格波动关联效应提供新的工具。

4.1 数据来源

按照现行CPI统计要求，目前广东省纳入CPI统计范围的代表商品品种大约有260种，在2006年对代表规格品进行过调整，增加和删除了部分代表品。为保持数据的连续性和一致性，按照最大公约数的方式，整理出纳入广东CPI统计的240种消费品从2007年1至2012年4月每月同比价格指数时间序列。

为方便研究，对上述240种商品分别从1-240编号，取2007年1至2012年4月上述240种商品每月同比价格指数作为时间序列，分别用A1,A2,…,A240表示，其中

A1=(a1,1,a1,2,…,a1,12),

A2=(a2,1,a2,2,…,a2,12),…,

A240=(a240,1,a240,2,…,a240,12)

4.2 构建消费品价格相关系数关联网络

以上述240种消费品作为网络的节点，分别取2001年1月至2012年4月上述240种商品(或部门)每月同比价格指数作为时间序列，两两求相关系数ρ(见公式4)，以相关系数ρ为边权，表示两种商品之间价格波动相关性大小(即此种商品上涨拉动彼种商品上涨的能力),某一商品自身边权为0(即network(i,i)=0)，得到相应相关系数矩阵R。取阈值P=0.007，当a(i,j)<0.7% ,节点i和节点j之间不连边，即边值net(i,j)=0；反之则连边，即边值为net(i,j)=1,建立0-1网络M4(见图3)。

图3 240种消费品价格相关系数关联网络M4拓扑图Fig.3 The topology diagram of correlation coefficient network M4 of 240 goods

4.3 运用网络传播模型测算价格波动关联效应

在阀值P=0.007时建立的网络，商品价格波动沿网络最短路并按照传播方程：Δpj=50%/distance(i,j)2传播，测算上述240种商品中每种产品依次上涨50%，对其余部门或商品的影响幅度。由于篇幅所限，这里只列举几种商品价格波动波及效应。以大米为例，当大米价格上涨50%，将波及其余149种商品，影响面粉、粮食制品价格上涨5.6%，影响猪肉、畜肉副产品、其它食品、鸡豆制品、植物油脂、植物油制品价格上涨1.4%，白酒价格上涨3.1%；当猪肉价格上涨50%，将波及其余164种商品，影响畜肉副产品价格上涨12.5%，带动植物油脂和植物油制品价格上涨12.5%，植物油脂和植物油制品价格受到比较大的影响与猪肉形成替代关系有关，测算数据与实际价格影响波及数据比较吻合。鸡只价格上涨50%，将波及其余163种商品，影响猪肉价格上5.6%，拉动畜肉制品价格上涨12.5%。其余鲜蛋、鲜菜、鲜果、白酒、衬衫、电冰箱(柜)、汽车、汽油、飞机票、宾馆住宿、水、电、液化石油气、管道燃气分别影响116、9、81、146、56、92、120、88、64、33、121、105、116、75个部门，相关影响幅度这里不在赘述。

5 结 论

本文建立了新的广东价格影响模型，测算了30个部门(或商品)相互间价格波动关联效应。运用网络表达了上述价格波动之间的相互关联关系，比较清楚地反映上述30个部门(或商品)之间波动的关联关系。构建了消费品价格波动关联效应网络传播模型，(即在阈值P=0.007时建立价格波动关联网络，按照商品价格波动沿网络最短路并依据传播方程：Δpj=50%/distance(i,j)2快速传播)，测算了240种消费品价格波动关联效应。研究可为解决以往研究大样本消费品价格之间的波动关联效应，需要大量拆并投入产出表难题，为开展价格波动关联效应研究提供简易测算方法。

同时文章在构建价格波动模拟网络时存在网络对称的问题，模拟精度需进一步提高，此外将30个部门模拟得到的价格波动网络传播规律能否直接推广到研究240种消费品价格波动关联效应，这些问题仍需要进一步研究，也是今后改进的重要方向。

[1] 刘向荣. 基于网络传播视角的广东消费品价格波动关联效应研究[D]. 广州：华南理工大学, 2013.

[2] 杨建梅，刘永清. 区域产业结构系统工程：理论与实践[M]. 广州：华南理工大学出版社, 1993.

[3] 顾海滨. 对投入产出价格变动模型的推导分析及评价[J]. 数量经济技术经济研究, 1994, 14:92- 95.

[4] 刘向荣，孙红英. 基于改进的BP神经网络中国CPI运行定量分析[J]. 数学的实践与认识, 2013, 43(6): 1-8.

[5] 孙红英. 两次金融危机影响下中国CPI运行对比分析[J]. 统计与决策, 2010, 1: 74-79.

[6] 孙红英，刘向荣，解玲丽. 基于传导模型的2010年价格指数预测[J]. 辽宁工程技术大学学报：自然科学版, 2010, 29(5): 941-944.

[7] 张红霞. 对投入产出价格影响模型的发展和改进[J]. 系统工程理论与实践, 2008, 1: 90-94.

[8] 韩一杰, 刘秀丽. 中国猪肉价格波动对其他部门产品价格及CPI 的影响测算[J]. 中国农村经济, 2011, 5: 12-20.

[9] 廖明球，王明哲. 多产品价格影响模型及其应用研究[J]. 统计研究, 2013, 30(2): 102-106.

[10] WATTS D J, STROGATZ S H. Collective dynamics of ‘small world’ networks [J]. Nature, 1998, 393(6684): 440-442.

[11] BARABáSI A L, ALBERT R, HAWOONG J. Mean-field theory for scale-free random networks [J]. Physica A, 1999, 272(1): 173-187.

[12] YANG J M, LU L P, WANG D X, et al. On competitive relationship networks: a new method for industrial competition analysis [J]. Physica A, 2007, 382(2): 704-714.

[13] 万阳松，陈忠. 上海A股市场股价波动相互影响能力实证研究[J]. 上海管理科学, 2006, 4: 29-30.

[14] LIU X R, SUN H Y. The leading nodes analysis of the consumer price volatility based on complex network[C]∥2012 IEEE fifth International conference on Advanced Computational Intelligence, nanjing, jiangsu China, 2012: 28-31.

[15] 孙红英，刘向荣. 消费品价格波动的关联效应分析—基于价格波动网络主导节点的实证研究[J]. 价格理论与实践, 2012, 2:41-48.

[16] 刘向荣，杨建梅，孙红英，等. 基于符号动力学的中国工业产品价格传导复杂网络分析[J].工业工程,2013,16(4): 49-55.

[17] 广东省统计局. 2007年广东省135部门价值型投入产出表[EB/OL]. (2010-03-08) [2013-10-15] http:∥www.gdstats.gov.cn/tjzl/tjfx/201003/t20100308_77821.html.