一种基于改进蚁群算法的山地三维路径规划算法

2014-03-26黄劲潮

荆楚理工学院学报 2014年2期

黄劲潮

(龙岩学院继续教育学院，福建龙岩 364012)

0 引言

当前社会，出现了很多自助游爱好者，他们需要在复杂的山地地形，寻找一条没有前人走过的路径来到达目的地。如何快速、准确的规划山地三维路径，成为一个值得研究的新课题。所谓三维路径规划，是在三维地图中规划出一条避开了无法通过的障碍，同时满足某些指标最优的三维路径。目前常用的路径规划算法，大多数只能规划二维平面路径;而一般的三维规划算法，大多运算算法复杂、需要很大的存储空间，同时无法在宏观全局角度来进行路径规划。目前常用的三维规划算法有粒子群算法、遗传算法、A*算法等，但粒子群算法与遗传算法只是准三维算法，而A*算法当维数增加时计算量会急剧增加［1－3］。本文在已有三维山地地图的基础上，采用一种改进的蚁群算法来解决上述问题。

1 改进的蚁群算法

Dorigo M等人在90年代初提出了蚁群算法，它是基于仿生蚂蚁搜索行为的一种进化算法。观察者发现，蚂蚁在搜索找寻食物时，会在爬过的路上留下分泌物，这种分泌物包含了蚂蚁的信息素。这种信息素会慢慢挥发，但是后续的蚂蚁能够检测到这种信息素的存在;并且后续蚂蚁会优先选择信息素浓度较高的路径点，同时它们在进过的时候还会再次留下信息素。这样该路径点的信息素浓度会不断增大，同时也会更加吸引后续的蚂蚁［4－5］。蚁群算法根据蚂蚁的觅食行为设计，它具有群体智能并有分布式计算的优点，因此它在路径选择上具有很大的潜力。

1.1 三维空间抽象建模

三维路径规划算法首先需要从三维地图中抽象出三维空间模型，模型抽象方法如下:首先三维地图左下角的顶点作为三维空间的坐标原点A，在点A中建立三维坐标系，其中，x轴为沿经度增加的方向，y轴为沿纬度增加的方向，z轴为垂直于海平面方向。在该坐标系中以点A为顶点，沿x轴方向取三维地图的最大长度AB，沿y轴方向取三维地图的最大长度AA’，沿z轴方向取三维地图的最大长度AB，这样就构造了包含三维地图的立方体区域ABCD–A’B’C’D’，该区域即为三维路径的规划空间。三维路径规划空间如图1所示。

三维路径空间建立起来之后，采用等分空间的方法从三维空间中抽取出三维路径规划所的网格点。首先沿边AB把规划空间ABCD–A’B’C’D’进行等分，得到n+l个平面∏i(i=1，2，…，n)，然后对这n+l个平面沿边AD进行m等分，沿边AA’进行l等分，并且并且求解出里面的交点。

通过以上步骤，整个规划空间ABCD–A’B’C’D’就离散化为一个三维点集合，集合中的任意一点对应着两个坐标，即序号坐标a1(i，j，k)(i=0，1，2，…，n，j=0，l，2，…，m，k=0，1，2，…，l)和位置坐标a2(xi，yi，zi)，其中，i，j，k分别为当前点a沿边AA、边AD、边AA’的划分序号。蚁群算法即在这些三维路径点上进行规划，最终得到连接出发点和目标点满足某项指标最优的三维路径。

图1 三维路径规划空间

1.2 信息素更新

蚁群算法使用信息素吸引蚂蚁搜索，信息素位置设定及更新方法对于蚁群算法的成功搜具有非常重要的意义。在1.1节中已经把整个搜索空间离散为一系列的三维离散点，这离散点为蚁群算法需要搜索的节点。因此，把信息素存储在模型的离散点中，每个离散点都有一个信息素的浓度值，该浓度值表征了对后续蚂蚁的吸引力，值越大，吸引力也越大，该值在蚂蚁经过改点后更新。

信息素在更新时可以采用全局更新或者局部更新两种方式。蚂蚁经过一个路径点时，信息素浓度降低，这就是局部更新。信息素浓度的降低是为了让蚂蚁们可以去探索未经探索过得路径点，在宏观全局角度来更好地规划线路。局部信息素更新随着蚂蚁的搜索进行，信息素更新公式为

其中，τijk是点(i，j，k)上所带的信息素浓度值;ζ是衰减系数。

蚂蚁搜索完一条完整的路径，以该路径的长度作为评价值，从路径集合中选择出最短路径，增加最短路径各节点的信息素值，这就叫全局更新。信息素更新公式如下:

其中，length(m)为第m只蚂蚁经过的路径长度;ρ为信息素更新系数;K是系数。

1.3 可视搜索空间

取z轴方向作为三维路径规划的主方向，探险者沿x轴方向前进，为了降低规划复杂程度，将探险者的运动简化为前向运动、横向运动和纵向运动三种运动方式。在前向运动一定单位长度距离Lx，max情况下，设定机器人最大横向移动允许距离为Ly，max，最大纵向移动距离为Lz，max。这样，当蚂蚁沿着x轴方向前进时，当位于点H(i，j，k)时，对下一个点的搜索就存在一个可视区域，可视区域如图2所示。

这样，当蚂蚁由当前点向下一个点移动时，可搜索的区域限制在蚂蚁搜索可视区域之内，简化了搜索空间，提了蚁群算法的搜索效率。

1.4 蚁群搜索策略

蚂蚁从当前点移动到下一个点时，根据启发函数来计算可视区域内各点的选择概率，启发数为

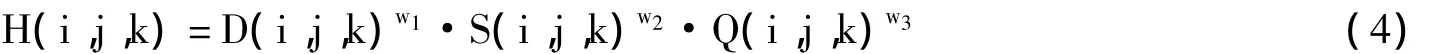
图2 蚂蚁搜索可视区域

其中，D(i，j，k)为两点间路径长度，促使蚂蚁选择距离较近的点;S(i，j，k)为安全性因素，选择点不可达到时，该值为0，促使蚂蚁选择安全点;Q(i，j，k)为下一点到目标点的路径长度，促使蚂蚁选择距离目标更近的点;wl，w2，w3为系数，代表上述各因素的重要程度。

D(i，j，k)的计算公式如下:

其中，a为当前点;b为下一个点。

S(i，j，k)的计算公式如下:

其中，Num表示在点(i，j，k)中可视点的数量;UNum表示可视点中不可达区域的点的数量。

Q(i，j，k)的计算公式如下:

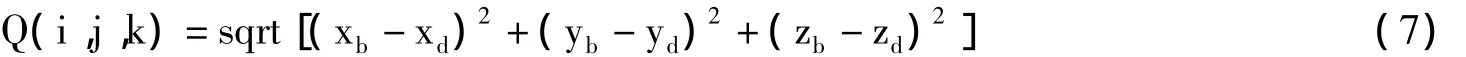
其中，b表示下一点;d表示目标点。

蚂蚁在平面∏i上的当前点pi选择平面∏i+1上下一个点pi+1的步骤如下:

1)根据抽象环境确定平面∏i+1内的可行点集合;

2)根据启发函数公式(4)依次计算点pi到平面∏i+1内的可行点集合的启发信息值Ha+1，u，v;

3)计算在平面∏i+1内任一点(i+1，u，v)的选择概率p(i+1，u，v):

其中τa+1，u，v为平面∏i+1点P(a+1，u，v)的信息素值。

4)根据各点的选择概率采用轮盘赌法选择平面∏i+1内的点。

1.5 算法流程

基于蚁群算法的三维路径搜索算法的算法流程如图3所示。

图3 三维路径规划算法

其中，三维环境建模模块根据1.1节抽取出三维环境数学模型;搜索节点模块根据启发函数搜索下个节点;信息素更新模块更新环境中节点的信息素值。

1.6 本设计对基本蚁群算法的改进

采用局部信息素与全局信息素相结合的更新策略，缩短了基本蚁群算法的计算时间，也避免了易陷于停滞的缺陷;基本蚁群算法信息素释放在节点边上，本设计把信息素释放在节点上，大大降低了运算量的同时也节约了存储空间。

2 山地三维路径规划设计

2.1 问题描述

采用蚁群算法在跨度为24 km×24 km的一片山地中搜索从起点到终点，并且避开所有障碍物的路径，为了方便问题的求解，取该区域内最低点的高度为0，其他点高度根据和最低点高度差依次取得。路径规划起点坐标为(1，10，800)，终点坐标为(21，4，1 000)，规划环境和起点、终点如图4所示。整个搜索空间为24 km×24 km的山地，其中，起点坐标为(1，10，800)，终点坐标为(21，4，1 000)。

图4 规划环境、起点、终点图

2.2 主要函数MATLAB编程实现

1)启发值计算函数

2)适应度计算函数

2.3 仿真结果

蚁群算法进行三维路径规划，规划空间范围为20 km×20 km的山地，把规划空间抽象为24 km× 24 km×2 km的规划空间，其中，x轴、y轴方向每个节点的间距为1 km，z轴方向每个节点间距为200 m。路径起点在规划空间的序号为［1 10 4］，终点在规划空间的序号为［21 4 5］。算法的基本设置为种群规模为20，算法迭代为400次，路径规划结果如图5所示。