伪渗滤孔隙门限理论在鄂尔多斯长8段低孔渗储层饱和度计算中的应用

陈凤陵

(中国石化华北分公司，河南 郑州 450006)

1 问题的提出

目前，测井含油气饱和度评价中广泛应用的主要方法仍然是20世纪40～50年代建立起来的储层孔隙度、饱和度和地层电阻率的实验关系，而且，这些实验关系的物理机制仍没有为人们完全理解。对于纯净碎屑岩和某些灰岩地层, 目前最常用的含水饱和度计算方法仍是Archie公式[1]和Archie-Winsauer[2-3]的实验关系(也称为Humble公式)。对于Archie公式(F=φ-m，m≈2)，目前还没有可信服的物理原理支持这种形式的幂率关系[4]。特别是广泛使用的Humble公式(F=0.62φ-2.15)，当φ=1时，F=0.625，这与φ=1,F=1的物理约束条件矛盾, 因此其适用性也受到一定限制[5]。另外，岩石中存在一定比例的不连通孤立孔隙时，孤立孔隙中地层水不导电，因此，电导率等于0时，孔隙度仍将大于零[5]。相反，在含泥质储层和骨架有导电矿物的储层中，即使孔隙度为零，仍然存在一定的导电性[6-7]。对于实际工作常常遇到的这两类储层，Archie公式[1]和Archie-Winsauer[2]的实验关系都无法描述，只有通过类似变胶结指数等变通措施加以应用。

几十年来，学者们对电导率-孔隙度-饱和度关系进行了深入研究[8-11]。针对饱和流体的泥质砂岩储层，Maxwell-Wagner利用实验数据，建立了等效介质电导率模型[12]。1968年，Hanai建立了电解液中存在导电颗粒的双相介质导电模型，即Hanai-Bruggeman模型[13-14](简称H-B电导率模型)。Lima等[15-16]建立了适用于粘土、泥质及泥质砂岩的导电模型。近来，国内也有多位学者开展了储层导电模型的研究[17-18]。然而，对于复杂孔隙结构低孔低渗储层，至今仍没有通用的电导率模型[19]。

本文通过不同类型岩石的岩电分析数据,基于效率理论及伪渗滤门限孔隙理论的分析，以鄂尔多斯盆地镇泾油田长8储层段为例，建立了由伪渗滤孔隙门限、含水饱和度、电导率三参数构成的低孔渗储层电导率模型。对镇泾油田多口井的长8低孔渗储层的实际资料应用表明，伪渗滤孔隙门限理论可以同时适用于存在孤立孔隙和泥质等具有导电骨架性的储层，为低孔低渗泥质砂岩储层的精细评价提供了一种新的方法。

2 经典岩电数据分析与伪渗滤门限理论

图1和图2分别给出了电阻率因素F和电导率因素f=1/F与孔隙度φ的双对数交会图和线性刻度图。图1看到，对小于20%的低孔隙度数据点，大多交会于拟合直线的上方，预示着对于低孔隙度岩性段，Archie公式[1]不能正确描述地层电阻率-孔隙度之间的关系。由图2的数据分布明显看到，地层电导率与地层水电导率比值(下称标准化电导率)，即地层电导率因素随孔隙度增大,表现更大的增加速率。在孔隙度小于20%的数据域f函数的斜率较小，孔隙度大于20%的数据域f函数的斜率明显变大。这种数据分布关系也预示着孔隙度大于0时电导率为0。

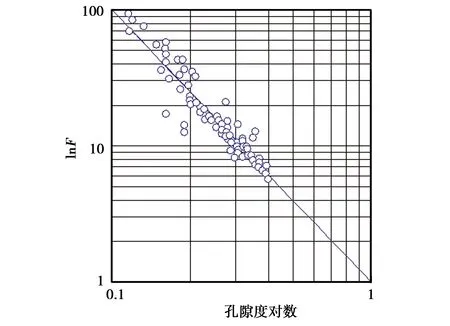
图1 Archie的Nacatoch砂岩数据计算的地层因素与孔隙度关系

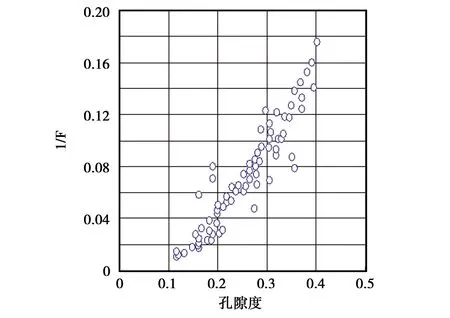
图2 Archie的Nacatoch砂岩数据计算的地层因素导数与孔隙度关系

那么什么机制造成上边的孔隙度-电导率响应特征呢？事实上，假设连通流体孔隙度的比例βc=φ-φϑ,φϑ是不导电部分孔隙度，那么，图2表示了标准化电导率对连通地层水体积分数的变化率与连通地层水体积分数近似成正比关系：

(1)

式中，φϑ是电流不导通的渗滤门限孔隙度，φ-φϑ是电流导通的连通地层孔隙度，α0是比例常数。

考虑到物理边界条件φ=1,σ0/σw=1及φ=φϑ时σ0/σw=0，对(1)式积分：

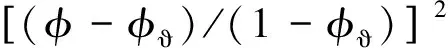
(2)

对于含油储层，(2)式对应的关系为：

(3)

式(2)中变量φ的范围为0≤φ≤1。事实上，φϑ不是真正的渗滤门限——即传导电流等于零的孔隙度值,而是孔隙度和标准化电导率交会图上从右端使电导率逼近于0的孔隙度值。因此，将(2)式定义的φϑ称为伪渗滤门限,(2)和(3)式称为伪渗滤门限理论(PPTT)[11]。

3 经典Archie公式的缺陷与修正

对于Archie公式，实际上没有考虑孔隙不连通或岩石中骨架中含有导电介质的情况，为了适应泥质砂岩的评价，考虑泥质的附加导电性，Winsauer[2]对Archie公式进行了修正，增加了2个可调参数α和m，即工业界常用的Humble公式[2]：

σ0/σw=α-1φm

(4)

其中，可调参数α和m使Humble公式更好地拟合观测数据。

然而，(4)式的Humble公式仍无法满足(φ，σ0/σw)=(1，1)的物理约束条件，而方程(2)的伪渗滤门限理论却包含了(φϑ，0)和(1，1)两个物理边界条件。图3中虚线表示了Humble公式和实线表示(3)式拟合Archie的Nacatoch砂岩数据得到的关系，图中看到，应用伪渗滤门限理论，使m和φϑ之间建立了良好的匹配关系。若在式(2)引入一个额外的参数, 使函数的抛物线顶点可以位于σ0/σw=0轴上方或下方，则式(2)可以适用包含不连通孔隙的储层。将方程(2)中φϑ项由顶点的孔隙度和电导率坐标代替,分别记为φmin和σmin，则式(2)改写为[13]：

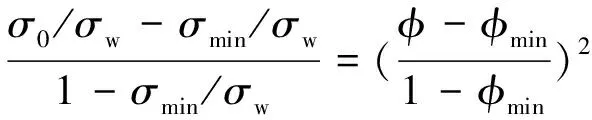
(5)

其中，σmin/σw是测量得到的最小标准化电导率，σmin是对应的孔隙度。当σ0/σw→1时，方程(5)的左边为1，当σmin→0时，左端退化为σ0/σw，(5)退化为Archie公式。而且，当数据点拟合趋势为负截距(φϑ<0)，或者甚至与孔隙度轴不相交，(5)式对应于储层骨架中存在导电矿物的情况。

4 伪渗滤门限理论在低孔渗储层含水饱和度评价中的应用

下边以镇泾油田和渭北油田的长8储层为例，说明伪渗滤门限理论在低孔渗储层含水饱和度评价中的应用。

4.1 储层孔隙度计算的骨架体积模型

根据研究区的薄片分析资料，长8储层岩石主要由以下几部分组成：石英、钾长石、斜长石、碎屑岩屑、云母以及孔隙中所含的流体，体积模型如图4所示。

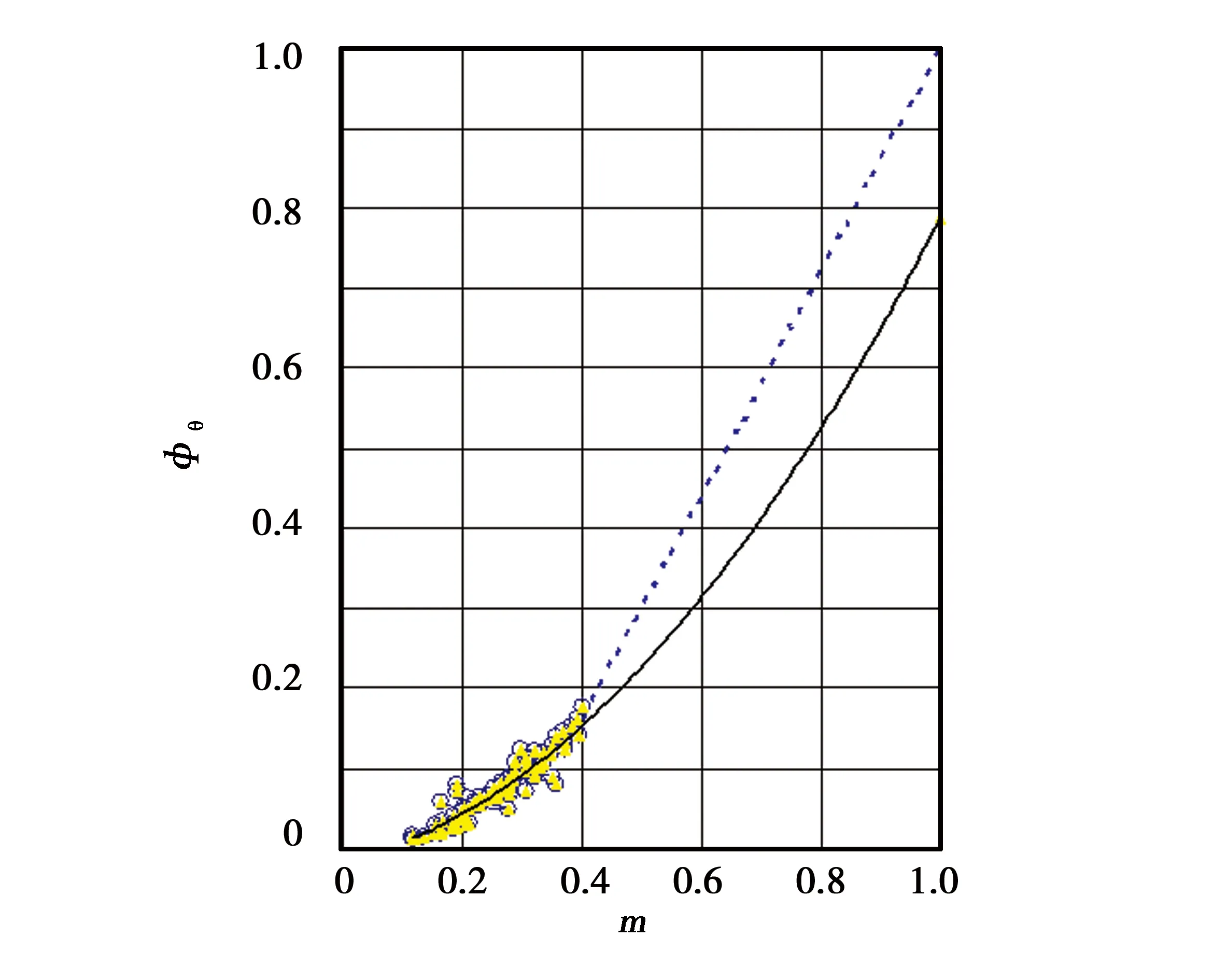
图3 Archie的Nacatoch砂岩数据得到的φθ/m关系

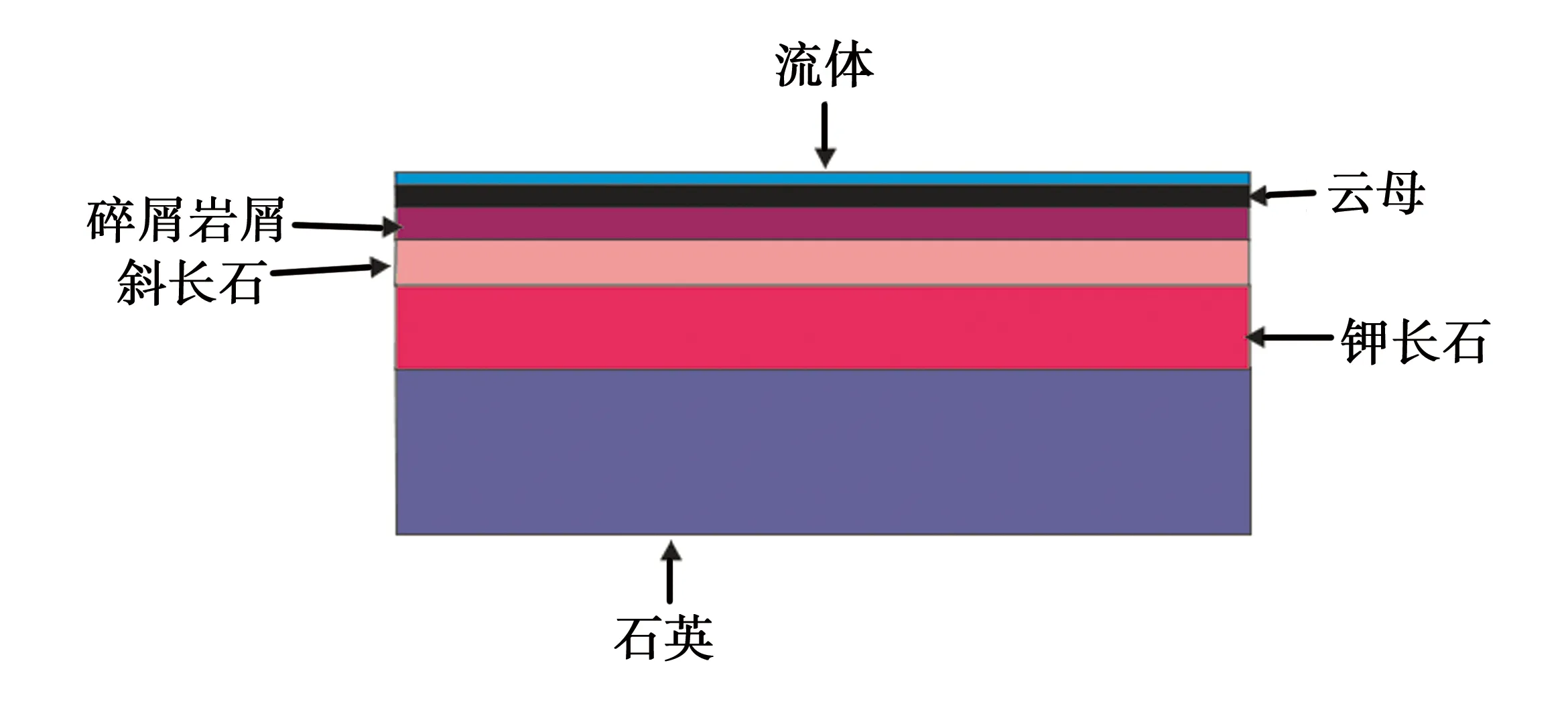
图4 岩石多元矿物模型

根据薄片分析数据与实验声波时差测量数据，建立声波时差与组分百分含量的关系(6)，找出岩石碎屑岩屑的测井物理参数。

ΔtT=ΔtQ×V1+Δtk-f×V2+ΔtP×V3+Δtm×V4+Δty×V5+Δtf×V6

(6)

式中，ΔtT——实测声波时差，μs/m；ΔtQ——石英声波时差, μs/m；Δtk-f——钾长石声波时差, μs/m；ΔtP——斜长石声波时差, μs/m；Δty——云母的声波时差, μs/m；Δtf——流体的声波时差, μs/m； Δtm——岩石碎屑岩屑的声波时差, μs/m；V1——石英体积,%；V2——钾长石体积,%；V3——斜长石体积,%；V4——岩屑体积,%；V5——云母体积,%；V6——流体体积,%。

利用薄片分析资料拟合公式(6)，得到岩屑的声波时差为：Δtm=191.0 μs/m，图5给出了(6)预测的结果和测井数据的对比。由于薄片分析数据和测井数据在深度上有一定的误差，在误差内Δtm=191.0 μs/m可以认为是可靠的。

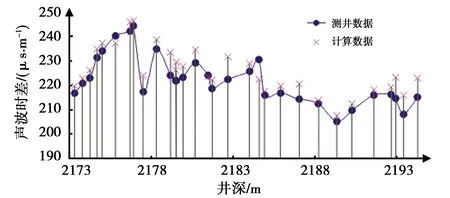
图5 公式(6)预测数据和测井声波时差的对比

骨架密度参数求取也是采用与声波类似的方法，根据地区的薄片分析资料，建立与(6)类似的公式(7)进行多元线性回归，找出岩屑的测井密度参数。

ρT=ρQ×V1+ρk-f×V2+ρP×V3+

ρm×V4+ρy×V5+ρf×V6

(7)

式中，ρT——总密度，g/cm3；ρQ——石英密度，g/cm3；ρk-f——钾长石密度，g/cm3；ρP——斜长石密度，g/cm3；ρm——岩石碎屑岩屑密度，g/cm3；ρy——云母密度，g/cm3；ρf——流体密度，g/cm3。

由薄片分析数据得到岩屑的密度ρm=2.625 g/cm3，图6是根据(7)式计算的参数与测井数值对比，两者吻合较好。用同样的方法计算中子响应参数，得到了表1所示的复杂岩性不同组分的岩石骨架参数。

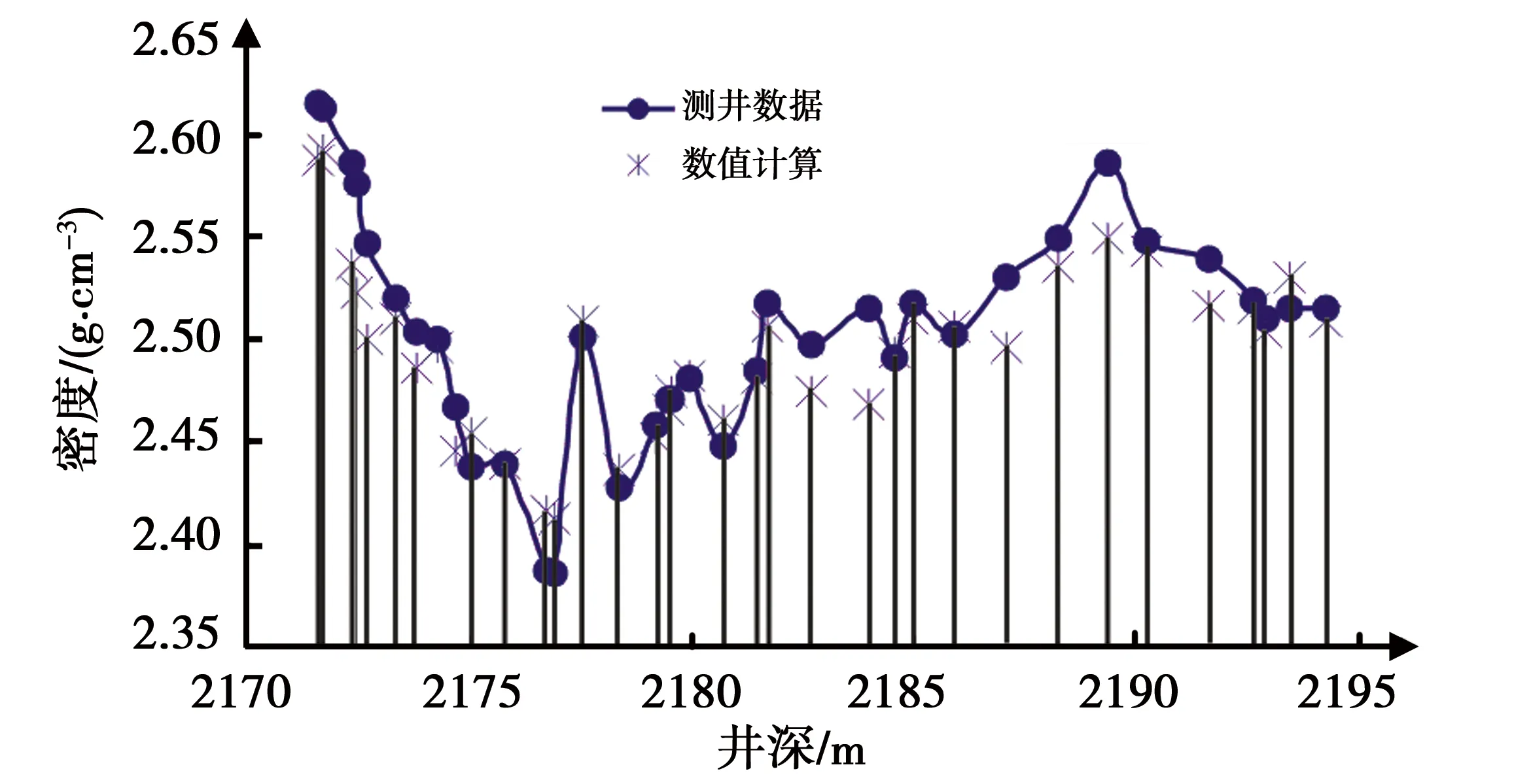
图6 计算数值与测井数值对比

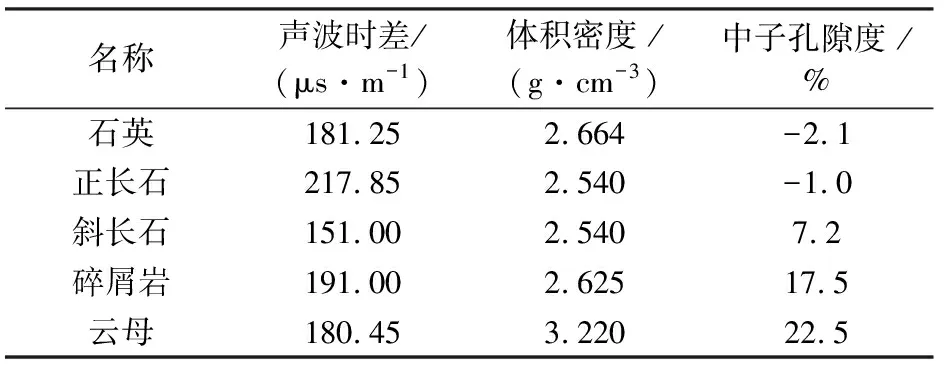
表1 岩石组分骨架参数

4.2 饱和度计算及应用

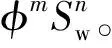
(8)

表示成地层评价中的含水饱和度的形式：

(9)

为了验证伪渗滤孔隙门限理论导出的饱和度关系的适用性，图7给出了镇泾5井长8含油层段的处理结果，第六道给出了Archie计算含油饱和度(蓝线)、伪渗滤孔隙门限理论计算的含油饱和度(红线)与密闭取心含油饱和度的对比(红色离散线)，从图中可以看到伪渗滤孔隙门限理论计算的含油饱和度更为可靠。

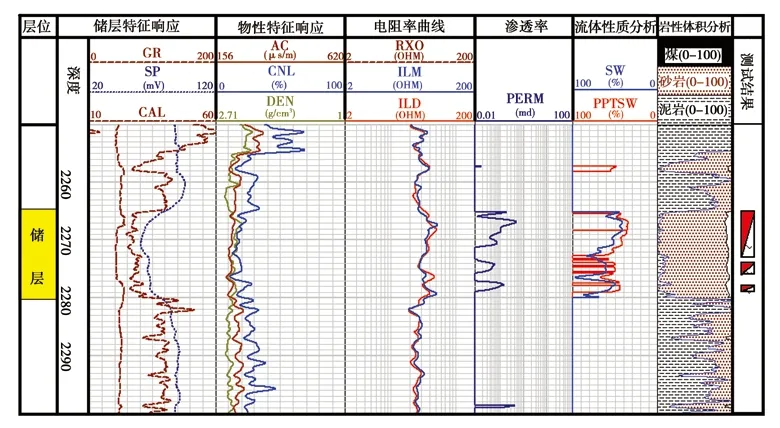
图7 镇泾5井长8段Archie饱和度、伪孔隙门限理论饱和度与岩心实验含油饱和对比

5 结束语

以伪渗滤孔隙门限理论为基础，将标准化电导率的变化与连通孔隙导电流体的体积变化比值与连通导电流体的体积建立正比关系，用于描述低孔隙度储层的导电性响应特征。为适应低孔隙度泥质砂岩储层含油气饱和度计算的要求，在伪渗滤孔隙门限理论中考虑了不连通孔隙和岩石导电骨架两个因素，并附加了两个自由变量表达复杂孔隙岩石的导电机制。文中讨论的伪渗滤孔隙门限理论PPTT将导电流体体积作为导电相的整体单元，避免了Archie-Winsauer公式把孔隙与流体饱和度当作不等权对待的缺陷。从鄂尔多斯镇泾油区的长8段低孔低渗储层的应用结果看到，文中伪渗滤孔隙门限理论导出的饱和度关系，不仅更好地拟合了经典Archie关系的实验数据，对镇泾的低孔低渗长8储层也取得了更好的应用效果。

[1] Archie G E.The electrical resistivity log as aid in determining some reservoir characteristics[J].Trans.AIME,1942,146：54-62.

[2] Archie G E.Introduction to petrophysics of reservoir rocks[J].Bullietin of AAPG, 1950,39(5):943-961.

[3] Winsauer W O,Shearin H M J, Masson P H,et al. Resistivity of brine saturated sands in relation to pore geometry[J].Bullietin of AAPG, 1952, 36(2):253-277.

[4] Herrick D C.Conductivity models, pore geometry, and conduction mechanisms[C].Paper D, in 29th Annual Logging Symposium Transactions: SPWLA, Houston,1998.

[5] Herrick D C, Kennedy W D. Electrical efficiency: a pore geometry theory for interpreting the electrical properties of reservoir rocks[J].Geophysics, 1994, 59(6):918-927.

[6] Hill H J, Milburn J D. Effect of clay and water salinity on electrochemical behavior of reservoir rocks[J].Trans. AIME, 1956,207: 65-72.

[7] Jin G,Torres-Verdin C,Devarajan S,et al. Pore-scale analysis of the Waxman-Smiths shaly-sand conductivity model[J].Petrophysics, 2007, 48(2):104-120.

[8] Waxman M L,Smits L J M, Electrical conductivity in oil bearing shaly sands[J].SPE Journal, 1968,(8):107-122.

[9] Clavier C,Coates G, Dumanoir J.Theoretical and experimental bases for the dual-Water model for Interpretation of shaly sands[C].SPE 6859, SPE-AIME conference, Denver, Colorado, Oct. 1977:9-12.

[10] Clavier C, Coates G,Dumanoir J.The theoretical and experimental bases for the electric dual-water model for Interimental of shaly Sands[J]. SPEJ, 1984, 24:153-167.

[11] Ioannidis M A,Kwiecien M J,chatzis I. Electrical conductivity and percolation aspects of statistically homogeneous porous media[J].Transport in Porous Media, 1997, 29(1):61-83.

[12] Dalla E, Cassiani G, Brovelli A,et al.Electrical conductivity of unsaturated porous media:pore-scale model and comparison with laboratory data[J].Geophysical Research Letters, 2004, 31(5):56-69.

[13] David K.The porosity-resisitivity-saturation relationship-An alternative to Archie's model[J].Petrophysics,2007,48(5):335-361.

[14] Diederix K M.Anomalous relationships between resistivity index and water saturations in the rotliegend sandstone[C].The 23rd Annual Logging symposium Transactions,SPWLA, London, 1982, Oct. 17-20,Paper X.

[15] Lima O A L. Water saturation and permeability from resistivity, dielectric and porosity logs[J].Geophysics, 1995, 60(11):1756-1764.

[16] Lima O A L, Michael B C, Geraldo G N, et al.A volumetric approach for the resistivity response of freshwater shaly sandstones[J].Geophysics, 2005, 70(1):1-10.

[17] 范业活,关继腾,房文静.含水泥砂岩导电特性的机理研究[J].青岛大学学报(自然科学版)，2005,18(2)：57-64.

[18] 朱家俊,耿斌,耿生臣,等.宏观导电机理下的泥质砂岩含水饱和度解释模型[J].石油勘探与开发，2003,30(4)：75-77.

[19] 宋延杰,王秀明,卢双舫.骨架导电的混合泥质砂岩通用孔隙结合电阻率模型研究[J].地球物理学进展，2005，20(3)：747-756.

[20] Myers M T.Pore combination modeling: extending the hanai-bruggeman equation[C].SPWLA 30th Annual Logging Symposium,1989, June 11-14, Paper D.