具有借贷限制的多阶段M-SAD投资组合决策研究
2014-03-26张鹏,田边
张 鹏,田 边
( 武汉科技大学管理学院,湖北 武汉,430081)
投资组合是分散投资风险的有效途径。20世纪50年代,Markowitz[1]使用方差来度量投资风险,提出了均值-方差单阶段投资组合理论,奠定了现代金融学的基础。但在实际的金融市场中,投资是一个持续不断、贯穿多阶段的过程。相对单阶段投资组合而言,多阶段投资组合是一个随机非线性的动态复杂系统,其优化求解要复杂得多。
目前,研究者运用了多种方法求解收益-风险型多阶段投资组合模型。Li等[2]提出终期财富最大化的多阶段安全首要模型,将该模型转化为目标函数可分离的动态规划问题,并运用动态规划的递推关系式求解;在文献[2]的基础上,Li等[3]又提出了多阶段均值-方差投资组合模型;Zhu等[4]提出具有破产风险控制的多阶段均值-方差投资组合模型;Wei等[5]提出假设资产收益率为Markov链且具有破产风险控制的多阶段均值-方差投资组合模型;Çelikyurt等[6]提出假设资产收益率为Markov链的多阶段均值-方差二次效用函数和安全首要模型,将该模型转化为目标函数可分离的动态规划问题,并运用动态规划方法求解。上述研究主要考虑终期财富最大化的模型,并且采用动态规划方法求解,但该方法存在“维数灾”和高阶非线性问题,对于解决大规模问题非常困难。Brandt等[7]运用扩大状态空间方法和模拟回归方法求解投资组合模型,并认为这种近似方法极大地减少了工作量,但随着时期数目的增加,该方法的误差也在增大;Yan[8]运用混合遗传算法求解多阶段均值-半方差投资组合模型;张鹏[9-10]采用自创算法——离散近似迭代法求解多阶段均值-方差和均值-半方差投资组合问题,并分析了该算法的收敛性和复杂性。
在上述研究的基础上,本文分别给出含有无风险资产且借贷利率相同和不同两种条件下的多阶段均值-半绝对偏差(M-SAD)投资组合模型,并运用离散近似迭代法进行求解。
1 多阶段M-SAD投资组合模型
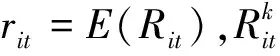
f(xt)表示第t期投资组合的方差,其表达式为:
(1)
U(rpt,f(xt))表示第t期投资者的效用函数,其表达式为:
U(rpt,f(xt))=βt[(1-ω)rpt-ωf(xt)]
(2)
式中:βt(0<βt≤1)为效用折扣因子;ω(0≤ω≤1)为风险偏好系数。βt=1表示一个效用单位在各个时期相同,ω=0表示投资者偏爱收益率最大而不管风险的大小,ω=1表示投资者极度厌恶风险。
一般情况下,可假设效用函数满足下式:
(3)
(4)
式(3)表示投资者的效用函数随着投资组合期望收益率的增加而增加;式(4)表示投资者是风险厌恶者,即随着投资组合期望收益率的增加,效用函数的增幅在减少。
借贷利率相同的多阶段M-SAD投资组合模型如下:
maxU(rpt,f(xt))
(5)
式中:r(w)=rbt=rlt;lt≤0;S0=1。
状态转移方程可以改写为:
(6)
在模型(5)中,第一个约束条件表示第t期投资组合期望收益率;第二个约束条件表示第t-1期和第t期末财富变化的状态转移方程;第三个约束条件表示无风险资产的借款比例不能超过预先给定的某个值;第四个约束条件表示第i种资产不允许卖空。模型(5)的经济含义是指,在满足上述四个约束条件的前提下,投资者应如何分配各种资产,使投资组合的总期望效用最大。
借贷利率不同的多阶段M-SAD投资组合模型如下:
maxU(rpt,f(xt))
(7)

模型(7)的第一个约束条件是非光滑的,可转化为如下两个光滑的线性规划问题。
maxU(rpt,f(xt))
(8)
和
maxU(rpt,f(xt))
(9)
2 多阶段 M-SAD投资组合优化
本文运用自创算法——离散近似迭代法求解多阶段M-SAD投资组合模型,并研究该算法的收敛性和复杂性。算法的具体步骤如下。
(1)将状态变量按照从小到大离散成4等份,即形成5个值[9-10]。
每阶段状态变量的最小值Stmin和最大值Stmax分别按照下面方法确定。
当投资者只考虑风险最小时,投资组合期望收益率也最小,此时第t阶段财富(状态变量)也最小。
minf(xt)
(10)
运用线性规划的旋转算法[11-12]可以计算出模型(10)的最优解,也可以计算出期望收益率的最小值,同时也得到了第t阶段状态变量的最小值。
当投资者只考虑投资组合期望收益率最大时,则第t阶段财富(状态变量)也最大。
maxrpt
(11)
运用线性规划的旋转算法可以计算出模型(11)的最优解,也可以计算出期望收益率的最大值,同时也得到了第t阶段状态变量的最大值。
(2)运用线性规划的旋转算法求出各状态值所对应的目标函数值,并构造多阶段有向赋权图。

(4)在上述最长路的基础上继续迭代。将第k+1次最长路的每阶段状态值与该阶段状态值的最小值和最大值分别等分成二等份并转(2)。
定理1离散近似迭代法是线性收敛的。
定理2设各阶段状态变量值离散成5个值,经过L次迭代可以逼近模型的最优解,则模型的复杂性为:需要L×(T-1)×52(3n+3)2(3n+2)+2(T-1)×52次加法,需要1/3L×(T-1)×52(3n+3)3次乘法,需要2×(T-1)×5(5-1)次比较。
证明:运用旋转算法求解线性规划问题(5)、(8)和(9),需要(3n+3)2(3n+2)次加法,需要1/3 (3n+3)3次乘法[15]。每次将各阶段状态变量离散成5个值,则T个阶段有向赋权图需要计算(T-1)×52个线性规划问题,如果经过L次迭代可以逼近模型的最优解,那么模型需要计算L×(T-1)×52个线性规划问题。T个矩阵βU1⊗β2U2⊗βTUT相乘需要2×52次加法;需要2×5(5-1)次比较。如果经过L次迭代,则需要2×(T-1)×52次加法,需要2×(T-1)×5(5-1)次比较。
因此,模型的复杂性为:需要L×(T-1)×52(3n+3)2(3n+2)+2(T-1)×52次加法,需要1/3L×(T-1)×52(3n+3)3次乘法,需要2×(T-1)×5(5-1)次比较。证毕。
3 算例
从上证50中选择6只权重股票,分别为股票1(武钢股份,600005)、股票2(浦发银行,600000)、股票3(中信证券,600030)、股票4(振华重工,600320)、股票5(中国平安,601318)、股票6(驰宏锌锗,600497),以2006年1月至2009年6 月(共14个季度)每一季度末收益率为样本数据,如表1所示(数据来源于广发证券至强版基本资料数据库)。
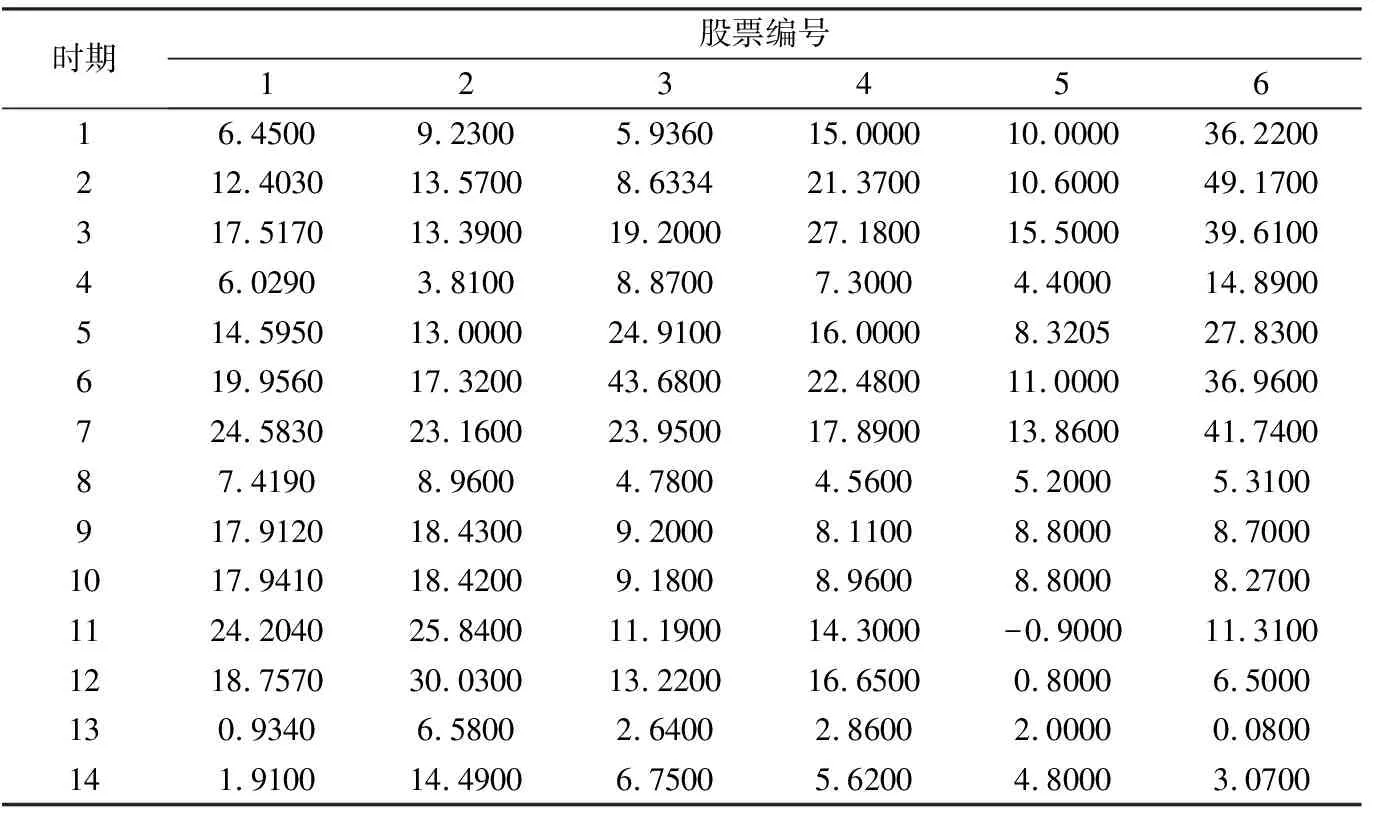
表1 6只股票的季度收益率(单位:%)Table 1 Quarter return rate of six stocks
采用移动平均法估计出6只股票未来四阶段的收益率。假设lt=-1,rlt=0.015,rbt=0.02,β=1,ω=0.8。
当ω=0.8、投资组合中含有无风险资产且借贷利率相同时,运用离散近似迭代法可以计算出五阶段投资组合最优投资策略和总效用函数如表2所示。
根据表2可知,当ω=0.8时,五阶段投资组合中第一阶段最优投资策略为:投资者借款无风险资产100%,分别购买第1只、第5只和第6只股票161.28%、0.10%和38.62%,不购买其它股票。同样可知其它阶段的最优投资策略。

表2 含有无风险资产且借贷利率相同的五阶段投资组合最优投资策略Table 2 Optimal investment strategy of multiperiod portfolio selection with risk-free asset and the same borrowing and lending rates
当ω=0.8、投资组合中含有无风险资产且借贷利率不同时,运用离散近似迭代法可以计算出五阶段投资组合最优投资策略和总效用函数如表3所示。

表3 含有无风险资产且借贷利率不同的五阶段投资组合最优投资策略Table 3 Optimal investment strategy of multiperiod portfolio selection with risk-free asset and different borrowing and lending rates
根据表3可知,当w=0.8时,五阶段投资组合中第一阶段最优投资策略为:投资者借款无风险资产100%,分别购买第1只、第5只和第6只股票161.17%、0.22%和38.61%,不购买其它股票。同样可知其它阶段的最优投资策略。
对比表2和表3可见,当投资组合含有无风险资产且借贷利率不同时,投资组合的最优投资策略、期望收益率和效用函数会发生变化。在实际市场中,借款利率大于贷款利率,因此,研究借贷利率不相同的情况是非常必要的。从表2和表3还可以看出,多阶段投资组合最优策略对于每种资产的期望收益率非常敏感,即当资产的期望收益率发生微小变化时,投资组合的最优投资策略发生了很大变化。因此,如何较正确地预测资产的期望收益率是非常重要的,也是今后需要重点研究的内容。
4 结语
本文综合考虑金融市场的实际情况,提出借款具有限制且借贷利率相同和不同两种情况下的多阶段M-SAD投资组合模型,并运用自创算法——离散近似迭代法求解,文中还证明了该算法的线性收敛性和复杂性,为求解多阶段投资组合模型提出了一种新的思路。最后,以一个具体的实例验证了算法的有效性,并得出以下结论:①当投资组合含有无风险资产且借贷利率相同和不同时,投资组合的最优投资策略、期望收益率和效用函数会发生变化;②多阶段投资组合最优策略对于每种资产的期望收益率非常敏感,即当资产的期望收益率发生微小变化时,投资组合的最优投资策略发生了很大变化。
笔者认为,以下三点值得进一步研究:①根据市场的实际情况,研究其它风险度量方法的多阶段投资组合决策;②研究交易成本和交易量限制等情况下的多阶段投资组合决策:③多阶段投资组合中每种资产期望收益率的预测方法。
[1] Markowitz H. Portfolio selection[J]. The Journal of Finance,1952, 7(1): 77-91.
[2] Li Duan,Chan Tsz-Fung, Ng Wan-Lung. Safety-first dynamic portfolio selection[J]. Dynamics of Continuous, Discrete and Impulsive Systems, 1998, 4:585-600.
[3] Li Duan, Ng Wan-Lung.Optimal dynamic portfolio selection: multiperiod mean-variance formulation[J]. Mathematical Finance,2000,10(3):387-406.
[4] Zhu Shu-Shang, Li Duan, Wang Shou-Yang. Risk control over bankruptcy in dynamic portfolio selection: a generalized mean-variance formulation[J]. IEEE Transactions on Automatic Control, 2004, 49(3):447-457.
[5] Wei Shuzhi, Ye Zhongxing. Multi-period optimization portfolio with bankruptcy control in stochastic market[J]. Applied Mathematics and Computation,2007,186(1):414-425.
[6] Çelikyurt U, Özekici S. Multiperiod portfolio optimization models in stochastic markets using the mean-variance approach[J]. European Journal of Operational Research , 2007,179(1):186-202.
[7] Brandt M W. Portfolio choice problems[EB/OL].[2014-01-12].http://citeseerx.ist.psu.edu/ view doc/download;jsessionid=611EB67E2632C0482CC04F2243AEADCB?doi=10.1.1.119.8765&rep=rep1&type=pdf.
[8] Yan Wei, Miao Rong, Li Shurong. Multi-period semi-variance portfolio selection: model and numerical solution[J]. Applied Mathematics and Computation,2007,194:128-134.
[9] 张鹏.多阶段M-SV投资组合优化的离散近似迭代法研究[J].经济数学,2008, 25(3):124-129.
[10]张鹏.基于离散近似迭代法的多阶段M-V投资组合优化[J].数学的实践与认识,2009,39(8):44-52.
[11]张鹏,张忠桢,岳超源. 限制性卖空的均值-半绝对偏差投资组合模型及其旋转算法研究[J]. 中国管理科学,2006,14(2):7-11.
[12]张鹏.不允许卖空情况下均值-方差和均值-VaR投资组合比较研究[J].中国管理科学,2008, 16(4):30-35.
[13]Heidergott B, Olsder G J, van der Woude J. Max plus at work: modeling and analysis of synchronized systems: a course on max-plus algebra and its applications[M]. Princeton: Princeton University Press,2006.
[14]Qin Yuyuan. Optimum path problems in networks[M]. Wuhan: Hubei Education Press,1992.
[15]张忠桢.凸规划-投资组合与网络优化的旋转算法[M].武汉:武汉大学出版社,2004.
