基于RBF神经网络软测量模型在超声氧浓度计的应用

郁永斌，和卫星，张 翔，汤方剑

(江苏大学电气信息工程学院，江苏镇江 212013)

0 引言

如何准确测量氧气浓度是人们一直研究的问题。近年来随着科技发展和实验规模的逐步扩大，氧气浓度检测技术逐渐成熟，基于氧气化学性质所研制的电化学氧气浓度分析仪，如氧化锆氧浓度传感器，由于传感器容易老化，故存在着寿命较短的问题，而基于氧气在磁场中具有极高顺磁性的性质研发的顺磁氧气分析仪器则存在着结构复杂、体积大、价格昂贵的问题，基于超声原理而研发的氧浓度传感器，其结构简单，寿命长、体积小，在很多应用场合具有其自身优势。

RBF神经网络结构简单[1]，有较快的收敛速度，具有全局逼近的性质和最佳逼近性能，非常适合于非线性系统的建模，它克服BP神经网络存在网络学习速度慢、容易陷入局部最小和隐含层节点个数不易确定等而导致建立的软测量模型测量误差大等问题。文中提出的RBF神经网络拟合算法在超声氧气浓度计的应用很好地解决了这个问题。

1 超声氧气浓度计的检测原理

1．1 检测的理论依据

文献[2]提出的气体浓度超声检测法适用于二元混合气体，甚至多元混合气体中单种气体组分的微量检测，通过测量超声波在气体中的传播速度来得到氧气浓度。文中超声传播速度是通过测量超声波在定长管子中的传播时间来确定的，由于超声波传播速度会受气体温度的影响，通过对其分析，得知氧气浓度与温度、时间之间存在着某种非线性映射关系，记为：

f=(S，T)

(1)

式中：f为气体浓度；S为超声波在气体中传播的时间；T为检测到的温度。

根据大量实测超声时程和气路温度及其标准浓度计所得氧气实际浓度，通过网络的学习功能而获得模型参数。一旦确定了模型和参数，即可用超声定长时程和温度来获得被测气体的浓度。

1．2 氧气浓度的检测过程

氧气浓度的检测过程如图1所示，系统主要由超声波发送、接收电路，计时电路，滤波电路，放大电路、比较电路、微机处理电路和上位机组成。

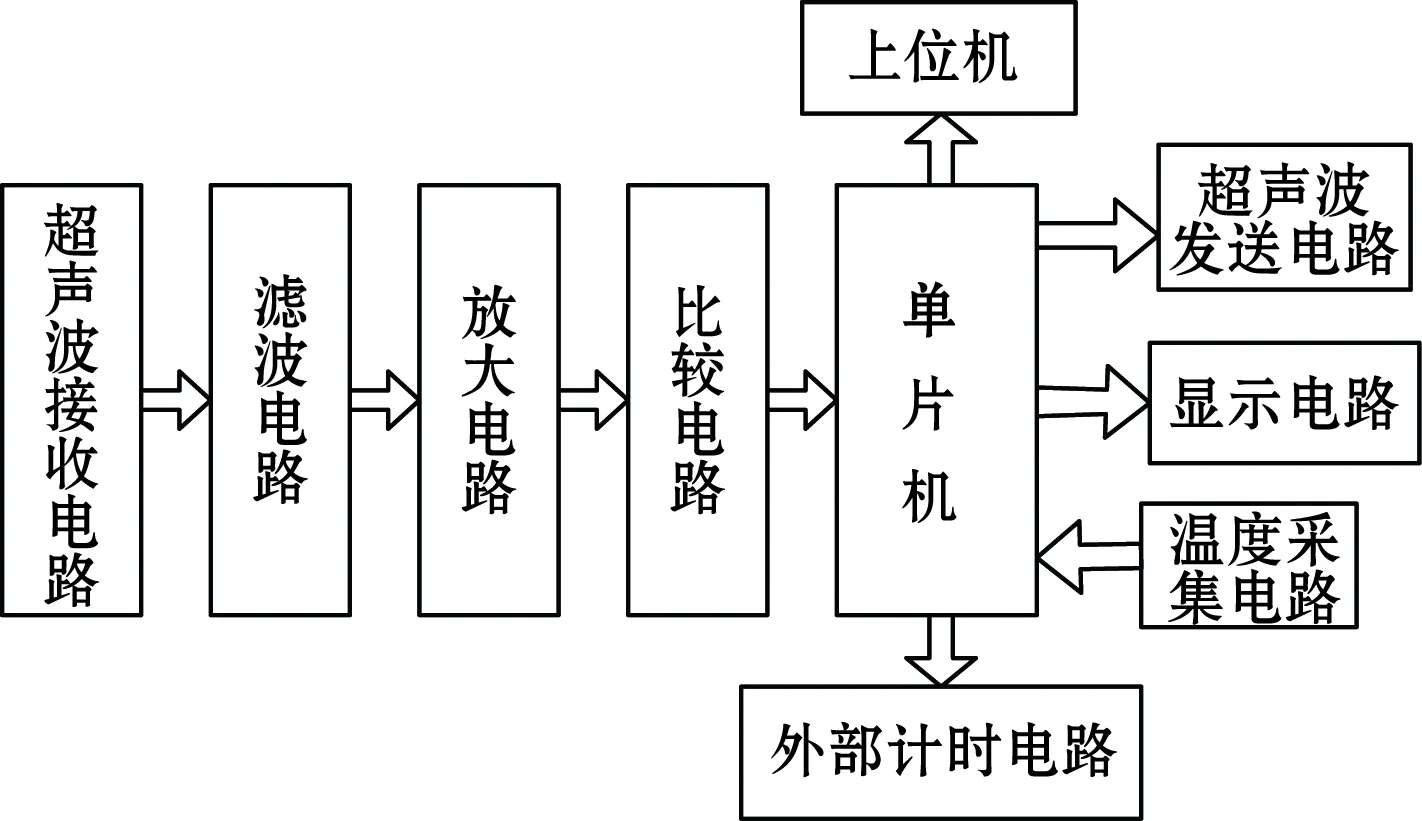
图1 超声波氧气浓度计检测流程图

整个系统上电时，单片机首先检查整个系统是否正常运行，如某个部位出错就报错并显示。如果电路运行正常，下位机给上位机发送一个正常运行命令，上位机接受命令后返回1个执行命令，这时整个系统开始运行。系统接收到运行指令后，先给超声换能器发送1个激励脉冲，同时给外部计时电路1个触发信号开始计时。此后单片机开始采集外界的温度并接收超声波信号，进而把接收的超声波信号经滤波、放大和比较后，由单片机计算出超声时程，所测时程与温度再经过串口发送给上位机进行数据处理，最后经式(1)计算出氧气的浓度。

2 基于RBF的氧浓度的软测量

2．1 RBF神经网络的结构及其算法

RBF神经网络属于前向神经网络类型，网络的结构与多层前向网络类似，是一种三层的前向网络[3]，它们分别为输入层、隐含层和输出层，其网络拓扑结构如图2所示。

图2 RBF神经网络结构

第一层是信号输入层，它由信号源节点组成；第二层是隐含层，隐含层节点数据视所描述问题的需要而定，隐含层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负非线性函数，该函数是局部响应函数；第三层为输出层，它对输入模式作出响应，是从隐含层到输出层，是线性变换。

RBF神经网络学习算法需要求解的参数有3个：基函数的中心、方差以及隐含层到输出层的权值。径向基函数中心选取的方法有多种，文中的自组织选取中心RBF神经网络学习法由2个阶段组成：自组织学习阶段，此阶段为无导师学习过程，求解隐含层基函数的中心与方差；有导师学习阶段，此阶段求解隐含层到输出层之间的权值。

径向基神经网络常用的径向基函数是高斯函数，高斯函数符合测量学中测量误差的正态分布特性，当输入信号靠近基函数的中心时，隐含层节点产生较大输出，当输入信号远离基函数的中心时，隐含层节点输出减小。由此可以看出，高斯函数对输入激励产生1个局部化的响应，即仅当输入落在输入空间中1个很小的制定区域时，隐单元才做出有意义的非零响应，故高斯函数在局部有具有很好的逼近能力。因此，径向基神经网络的激活函数可表示为：

(2)

式中：R(xp-ci)为高斯函数的宽度；‖xp-ci‖为欧式范数；ci为高斯函数的中心；σ为高斯函数的方差。

图2所示的RBF神经网络中有P个输入节点，M个隐含层节点，一个输出层节点，以高斯函数RBF传递函数，则整个网络的输出可表示为：

(3)

式中：X表示输入样本；‖·‖表示欧式距离；ci为网络隐含层节点的中心；ωij为隐含层到输出层的链接权值；yi为输入样本对应的网络的期望输出。

RBF神经网络的关键问题是径向基函数数据中心的选取以及权值的确定[4]。文中采用监督训练方法来确定RBF的中心以及网络的其他自由参数，具体算法如下。

首先定义一个目标函数ξ，使得：

(4)

式中：yi为网络输出的期望值；y(X)为当前的网络实际输出；N为训练样本数。

对网络学习的要求是寻求网络的自由参数，使得目标函数ξ达到极小，应用梯度下降法，可得网络各参数的算法如下：

(1)RBF网络数的各中心值的学习算法为：

(5)

(2)隐含-输出层的链接权值的学习算法为：

(6)

(3)径向基函数的宽度的学习算法为：

(7)

式中：η1、η2和η3为学习率；α1、α2和α3为动量因子，也称为遗忘因子。

2．2 氧气浓度的软测量模型

通过对氧气浓度检测机理及性质的研究分析可知[5]，影响氧气浓度的因素有很多，但主要的因素有超声波的传播时间、温度。文中选择这2个参量作为软测量的输入，用顺磁式高精度氧浓度分析仪所测氧浓度作为软测量模型的训练数据输出，则可以得到氧气浓度软测量模型如下：

N(t)=f(S(t)，T(t))

(8)

式中：N(t)为氧气浓度；S(t)为超声波在定长管道中传播的时程；T(t)为外界环境的温度；t为时间。

则由式(3)和式(8)可得氧气浓度的软测量模型：

N(t)=f(S(t)，T(t))

(9)

2．3 软测量模型的训练和校正

建立如图1所示的氧气浓度检测系统，对制氧机进行数据采集并建立软测量模型所需的辅助变量数据[6]，对采样数据中存在粗大误差的数据进行剔除、滤波以及归一化处理。试验中共采集了270组数据，其中135组数据作为训练样本，135组用于模型的检验与校正。

为检验氧气浓度软测量的精度，定义性能指标为：

ei=|yi-fi(X)|

(10)

ri=[yi-fi(X)]/fi(X)

(11)

式中：yi为第i个样本的实际输出；fi(X)为第i个软测量模型的输出；ei为第i个样本实际输出与模型输出的相对误差；ri为第i个样本实际输出与模型输出的绝对误差。

借助MATLAB的RBF神经网络工具箱[7]，完成对氧气浓度软测量模型的建立和离线训练，试验结果表明，RBF神经网络的训练速度很快，训练时间均小于2 s，软测量模型预测结果与校验数据对比结果如图3所示，软测量模型预测结果与校验数据相对误差如图4所示，绝对误差如表1所示。

图3 RBF软测量模型预测结果与校验数据对比

图4 RBF软测量模型预测输出与校验数据的相对误差

表1 RBF软测量模型预测输出与校验数据误差的对比统计

从图3看出，软测量模型预测的氧气浓度能够很好地匹配校验数据，且能够准确地实时跟踪氧气浓度的变化。由图4可知模型预测输出数据与试验数据的相对误差以及由表1可知模型预测的绝对误差绝大部分都小于1%。由此可证明，基于RBF神经网络的超声波氧气浓度软测量模型是有效的，且能达到很高的精度，能够满足实际的应用要求。

3 试验证明

为进一步验证基于RBF神经网络的超声波氧气浓度软测量技术的有效性和实用性，建立了可应用于工业现场的氧气浓度检测系统。现场采集140组数据，这些数据经过预处理后输入所建立的软测量模型，得到的输出与现场应用(M&C)的PMA 10型O2-Analyser所得的结果进行比较，如图5、图6以及表2所示。

图5 软测量结果与氧气浓度测试仪测量数据实际对比

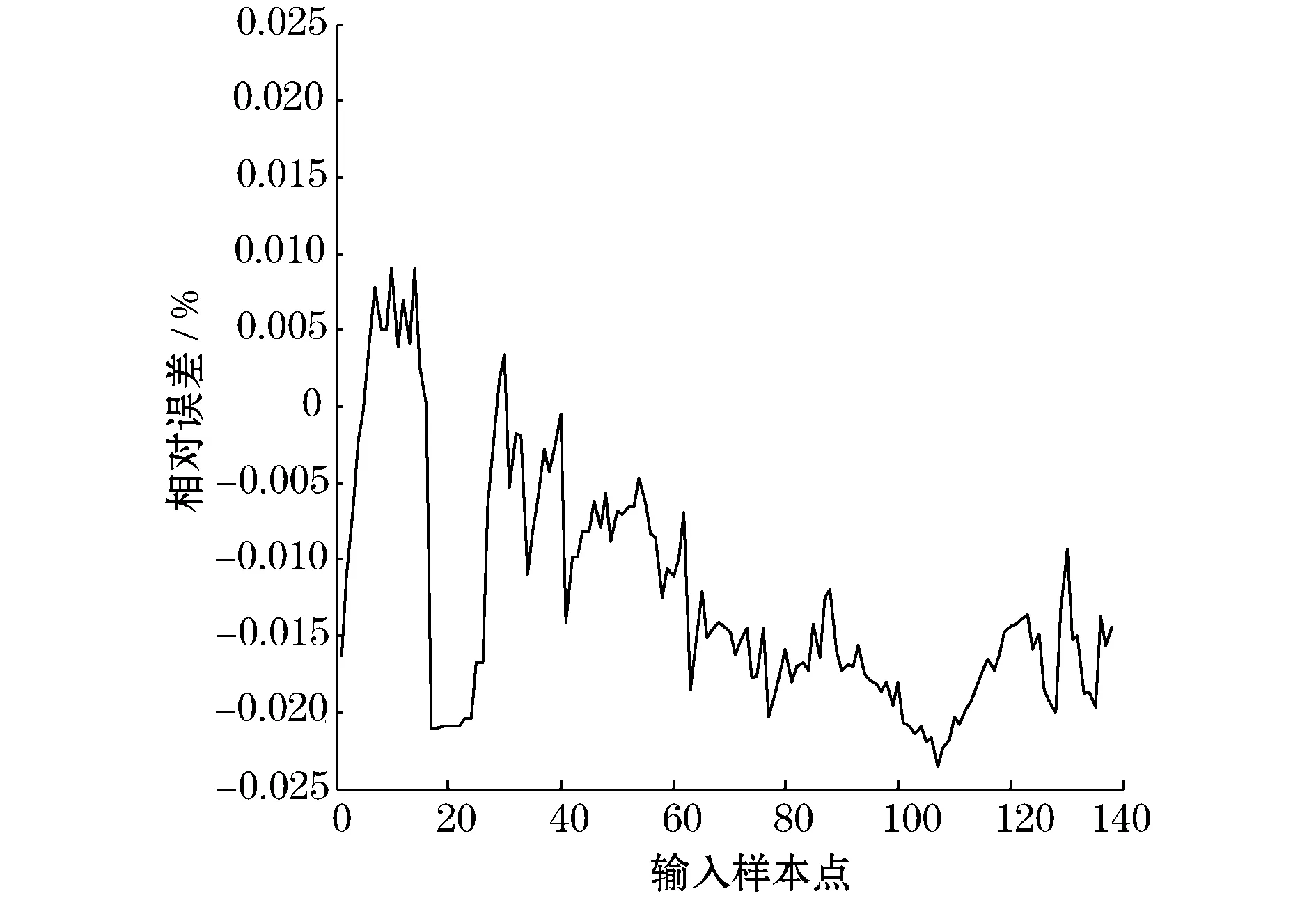
图6 软测量结果与氧气浓度测试仪测量数据的相对误差

表2RBF软测量模型预测输出与氧气浓度测试仪测量数据误差的对比统计

由图5可知，基于RBF神经网络的超声软测量技术检测氧气浓度的方法是可行的，并且长时间运行的零点稳定性好。由图6及表2所知，该方法测量精度较好，最大测量绝对误差与相对误差都小于等于1.5%，完全能够满足生产需要。

4 结束语

文中介绍的基于径向基函数神经网络的氧气浓度测量模型，采用带有遗传因子的梯度下降算法确定RBF网络模型的数据中心和连接权值，通过合理地选择数据中心的初值和隐含层，最终可以建立一个精确的拟合模型。

仿真和试验结果证明：所建立的氧气浓度软测量模型能够很好地匹配校验数据，可实时在线监测，维护方便，为氧气产生及应用过程实施闭环控制提供技术支持，提高了工业生产的自动化水平。

参考文献：

[1] 仝卫国，杨耀权，金秀章．基于RBF神经网络的气体流量软测量模型研究．中国电机工程学报，2006，26(1)：66-69．

[2] 江泽涛，胡景春，张少钦．超声波检测二元气体成份技术研究．南昌航空工业学院学报，2000，14(3)：223-226．

[3] CHEN S，BILLINGS S A．Neuarl networks for nonlinear dynamic system modeling and iddentificationg．Int J．Control，1992，56(2)：319-346．

[4] NIYOGI P F．On the relationship between generalization error，hypothesis complexity，and sample complexity for radial basis function．Neuarl Computation，1996(8):819-821．

[5] 张海传，刘钟阳，许东卫，等．基于RBF神经网络模型的臭氧浓度软测量研究．大连理工大学学报，2010，50(6)：1021-1023．

[6] POGGIO T，GIROST F．Networks for approximation and learnint．Proceedings of the IEEE，1990，78(9):1481-1497．

[7] 张小俊，张明路，李小慧．基于RBF神经网络的电化学CO气体传感器的温度补偿．传感技术学报，2009，22(1)：254-258．