基于数学形态滤波的电压闪变检测研究
2014-03-25黄耀东韩子骞
黄耀东,张 颖,韩子骞
(长沙理工大学 电气与信息工程学院,湖南 长沙410014)
0 引言
随着科技进步与社会的不断发展,电力系统中的冲击负荷日益增多,使得电网中电压波动与闪变更加频繁,严重影响电能质量,因此,需要对其进行检测与分析并提出具体的方案[1]。
目前,常用的闪变调制波检波方法有平方解调法、半波有效值法、全波整流法、小波变换法以及FFT 等[2],但它们应用于实际电网时都存在各自的缺陷与不足。
IEC 给出的闪变仪评价指标是基于统计型的(如短时闪变严重度和长时闪变严重度),这些指标无法体现闪变的具体参数,因此对研制闪变的装置以及治理闪变的策略并无实际的指导意义[3]。
Prony 算法实时性较高且需要原始数据较少,是一种基于最小二乘法的线性拟合方法,它能够提取并分析信号中的特征分量,因此在电能质量分析当中经常采用该方法。
针对Prony 算法在电压波动与闪变过程中对噪声敏感的缺陷,本文提出利用数学形态滤波法对采样信号进行处理,同时结合Hilbert 变换对闪变包络进行提取并利用Prony 算法分析提取去噪信号各频率分量的特征参量,仿真实验表明该方法的有效性与精确性。
1 电压闪变信号的数学模型
一般而言,电压闪变实际上可看作是正弦电压的低频调制,其数学模型表达如下:
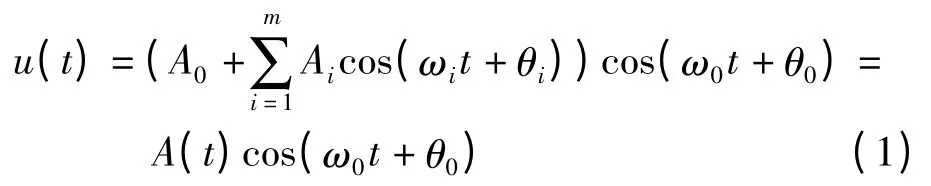
式中:A0,ω0分别是基波电压幅值和角频率;Ai,ωi分别为调幅波电压的幅值与角频率。调幅波幅值最大约为基波的10%,角频率一般为1~10 Hz。根据上述可知,闪变信号可看作是低频幅值调制窄带信号,因此满足Hilbert 变换条件[4]。但是当信号中有噪声时必须对其进行有效滤波才能保证Hilbert 变换的准确性以及Prony 分析的精确性。
2 数学模型数学形态学滤波
2.1 数学形态学理论基础
数 学 形 态 学[5](Mathematical Morphology,MM)是由数学集合理论与函数理论的基础上发展而来的一种新型数学方法。形态学滤波算法能有效消除信号的背景噪声且计算速度快,同时能够保持图形与图像信号主要的特征。数学形态学的原理是利用结构元素(“探针”)收集信号特征,通过探针不断移动搜索信号之间的关系,提取信号信息并描述信号特征。因此被广泛的应用到实际的各个领域当中[6,7]。
MM 的运算包含4 种基本操作处理方式,其运算方式包括膨胀运算、腐蚀运算、开运算以及闭运算,运算处理过程方式不同则产生的效果也不同。根据n 维欧氏空间与高等数学理论及性质,设子集合A 和B 在欧氏空间Rn范围中,则形态学膨胀运算和腐蚀运算可以用表达式A 和B 来演示:
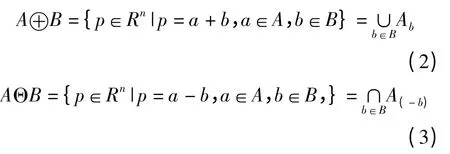
式中:⊕,Θ 代表膨胀和腐蚀运算。腐蚀对信号内部作滤波处理,具有收缩信号作用,膨胀对信号外部作滤波处理,具有扩张信号作用。形态学开运算与闭运算分别定义为:

式中:符号○与·分别代表开运算和闭运算。
2.2 形态学滤波器的构造
定义原始信号f(x)为Df上的离散函数,结构元素g(x)为Dg上的离散函数,且有Df,Dg分别为f(x)与g(x)的定义域。根据不同顺序级联开、闭运算,定义了形态开-闭与形态闭-开滤波器。

滤波器通过构造开-闭运算与闭-开运算滤除正负脉冲噪声。由于开运算的收缩性导致开-闭滤波器的输出偏小,闭运算的扩张性导致闭-开滤波器的输出偏大,因此直接影响滤波器的去噪性能。所以采用开-闭与闭-开组合形态滤波器对信号进行非线性滤波[8]。

式中:f(x)为含噪声的原始输入信号;y(x)为形态滤波器的输出信号。
2.3 结构元素的选取
结构元素包括形状和尺寸两方面,形状和尺寸的选取直接影响滤波器的滤波效果[9]。结构元素有直线、斜线、曲线(如正弦、余弦等)、圆形、三角形以及其他多边形(如矩形、六角形、菱形等)等。在腐蚀和膨胀过程中结构元素需要左右翻转和平移,因此结构元素应具有良好的对称性以满足其作为“滤波窗”的作用。
经验表明,与其他形状相比,圆形结构对毛刺及边界点具有较好的抑制作用,因此选用圆形结构作为结构元素的形状。同时,为了验证其具有较好的平滑效果,利用三角形结构元素与直线形结构元素与其进行滤波比较,并以信噪比作为参考标准,结果如表1 所示。
从表1 可以看出:圆形结构的滤波效果优于三角形与直线型结构的滤波效果。

表1 不同形状结构元素滤波器去噪结果
图1 为圆形结构元素滤波器的滤波仿真结果。由图1 可以看出:圆形结构元素滤波器具有良好的滤波效果,对噪声起到有效的抑制作用。

图1 圆形结构元素滤波器滤波仿真图
3 Prony 算法
3.1 Prony 算法基本原理
扩展Prony 算法[10~12]的数学模型采用的是一组具有任意幅值、频率、相位和衰减因子的指数函数,其离散时间函数形式如下:

式中:bi=Aiexp(jθi);zi=exp[(αi+j2πfi)Δt];Ai代表幅值;θi代表相位;αi代表衰减因子;fi代表震荡频率;Δt 代表采样间隔。定义一代价函数,令误差平方和ε=0,即可求得四元组参数(Ai,θi,αi,fi)。定义一常系数线性差分方程式如下:

算法的重点为常系数线性差分方程式(10)的齐次解为式(9)的拟合。定义:式(10)中参数a1,a2,…,ap的最小二乘估计准则是使得误差平方和最小。定义:i),n=p,…,N-1,那么求解方程Xa=ε 的线性最小二乘法称作扩展的Prony 算法。定义样本函数为),i,j=0,1,…,p,通过输入信号构造r(i,j)与扩展阶矩阵Re(pe≫p):

利用SVD-TLS 算法求取Re的有效秩与系数a1,a2,…,ap的总体最小二乘估计,然后求特征多项式1 +a1z-1+a2z-2+…+apz-p=0 的根,同时通过递推差分方程(10)求出,n =1,2,…,N-1,且有,再求取的最小二乘解,得到参数b1,b2,…,bp最终计算各个频率分量的四元组参数:AI= |bi|,θi=arctan[Im(bi)/Re(bi)]/(2πΔt),αi=In|zi|/Δt,fi=arctan[Im(zi)/Re(zi)]/(2πΔt)。
3.2 Hilbert 变换原理-闪变包络线的形成

4 算例仿真分析
在MATLAB7.0 平台上进行编程仿真,对原始信号与含噪信号进行仿真分析来验证算法的可行性与有效性。采样信号的频率为1 000 Hz,信号采样时间为200 s,基波的频率为50 Hz。
4.1 对原始信号进行Prony 算法仿真分析
电压闪变信号选取单一低频幅值调制的电压信号,如下所示:

由表2 可以看出,闪变信号经Prony 分析得到一个幅值为1(p.u.),频率为50 Hz 的基频载波分量,以及频率分别为40 Hz 和60 Hz,幅值为0.1 的两个低频间谐波调幅波分量,且两间谐波的相位和衰减系数均接近为零。仿真分析显示,在不受噪声干扰情况下Prony 算法可以准确估计出闪变信号各频率分量的特征参数。

表2 原始信号的Prony 分析结果
原始信号的Prony 拟合图如图2 所示。Prony拟合精度高,且信号几乎与原始信号重合,同时Hilbert 变换提取出的闪变信号包络线能够精确地体现闪变信号的变化。

图2 原始信号的Prony 拟合
4.2 基于数学形态滤波和Prony 分析的仿真分析
在原始信号基础上添加均方差为0.3,均值为0 的随机噪声,并对含噪信号以及3 种形态学滤波后的信号进行仿真分析比较,结果如表2所示。
从表3 可以看出,对含噪信号得Prony 分析误差较大,存在波动现象,且在估计40 Hz 频率分量时,幅值的相对误差达到427.60%。采用数学形态滤波处理后的Prony 分析均较为准确,与去噪前相比较,频率与幅值估计的相对误差明显下降。仿真分析表明Prony 算法易受噪声影响,采用数学形态滤波进行去噪预处理可以有效提高Prony 分析特征参数的精确度。圆形结构滤波器与Prony 分析结合较三角形、直线形与之结合分析的效果好,更加稳定,且频率估计的相对误差均在1.6%以内,幅值估计的相对误差均低于其他两种滤波后的估计误差,因此,该方法具有更精确的分析效果。

表3 含噪声信号的Prony 分析结果
图3 为含噪信号通过Prony 拟合得到的仿真图,由图3 可以看出Prony 分析算法易受噪声影响,其拟合信号的效果不佳,与原始信号误差较大。

图3 去噪前信号的Prony 拟合

图4 去噪后信号的Prony 拟合
图4 为圆形结构滤波去噪后信号的Prony 拟合仿真图,由图4 可以看出,经过形态滤波预处理后,Prony 拟合信号比较平滑且与原始信号较为接近。仿真表明,将数学形态滤波法与Prony 算法结合可以改善Prony 算法对噪声敏感的问题,从而提高电压闪变检测的精确性。
5 结论
利用数学形态滤波方法对含噪声的电压闪变信号进行去噪预处理,并结合扩展Prony 算法与Hilbert 变换进行检测与分析,弥补了Prony 算法对易受噪声影响的缺陷,实现了对闪变信号检测与分析。仿真结果表明,该方法可以提高Prony算法的有效性与精确性,同时能够分析信号特征参数并提取闪变包络,是一种有效的电压闪变检测分析方法。
[1]肖湘宁,韩民晓,徐永福.电能质量分析与控制[M].北京:中国电力出版社,2004.
[2]舒泓,王毅.基于数学形态滤波与Hilbert 变换的电压闪变测量[J].中国电机工程学报,2008,28(1):111-114.
[3]沈杨,戴本祁,张惠东.基于小波和扩展Prony 算法的电压闪变检测新方法[J].电力系统保护与控制,2010,38(10):43-47.
[4]王秉均.通信原理及其应用[M].天津:天津大学出版社,2000.
[5]崔屹.图像处理与分析:数学形态学方法及应用[M].北京:科学出版社,2002.
[6]于湘涛,褚福磊,郝如江.基于柔性形态滤波和支持矢量机的滚动轴承故障诊断方法[J].机械工程学报,2009,45(7):75-80.
[7]陈平,李庆民.基于数学形态学的数字滤波器设计与分析[J].中国电机工程学报,2005,25(11):60-65.
[8]黄艳菊,孙强.数学形态学滤波在电压闪变检测中的应用[J].机电产品开发与创新,2011,24(4):143-145.
[9]吴国洋.基于粒子群优化的形态学滤波器消噪方法[J].机械传动,2012,36(8):101-104.
[10]张贤达.现代信号处理[M].北京:清华大学出版社,2002.
[11]Tayjasanant T,Wang W C,Li C,et,al.Interharmonic-flicker curves[J].IEEE Transactions on Power Delivery,2005,20(2):1017-1014.
[12]刘建雄,张有兵,翁国庆,等.基于Prony 算法的电压闪变检测方法研究[J].机电工程,2008,25(6):54-57.
[13]Feilat E A.Detection of voltage envolope using prony analysis-hilbert transform method[J].IEEE Transactions on Power Delivery,2006,21(4):2091-2093.
