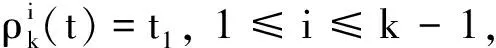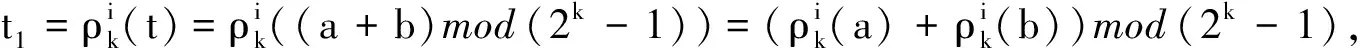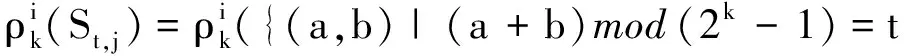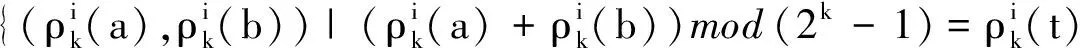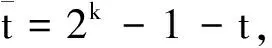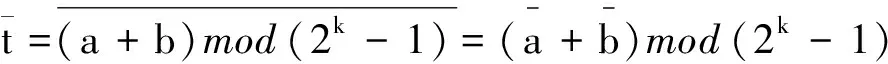源于密码学的组合数猜想问题中的数据特征
2014-03-25邓宇龙张晓朋郑玉军
邓宇龙, 张晓朋, 郑玉军
( 湖南科技学院数学与计算科学系 计算数学研究所, 湖南 永州 425199 )
0 引言
Tu和Deng[1]提出了源于密码学的组合数猜想:
猜想1设St,k={(a,b)|a,b∈Z2k-1,a+b≡t(mod 2k-1),w(a)+w(b)≤k-1}, 其中1≤t≤2k-2,k≥2,w(t)是t的Hamming权,则集合St,k的基数#St,k≤2k-1.
根据文献[1]的猜想,Tu和Deng获得了两类具有最优代数免疫的Boolean函数类:一类仍然是Bent函数类,另一类是具有最优代数次数和目前所知最好的非线性度(这个结果优于文献[2]给出的函数类非线性度)的平衡Boolean函数类.但是,对于猜想1的证明,文献[1]仅仅只是给出了transfer-matrix算法,然后利用计算机辅助,机械地验证了k≤29的情况,这与猜想1的结论还有很大的差距.
观察猜想1中集合St,k的构造发现,b由a唯一确定,因此设想猜想1的结论可以通过对整数a的个数的计算来获得.源于这种想法,文献[3]把a划分成两类:第一类为a=0,1,…,t,b=t-a; 第二类为a=t+v,b=2k-1-v,v=1,2,…,2k-t-2.根据这两类划分,文献[3]证明了当t的权w(t)较小时(w(t)≤3)猜想1的结论成立,并且还指出a的个数的统计很大程度依赖于
1 背景知识
引理1[3]w(2k-1-x)=k-w(x), 0≤x≤2k-1; 当xi=1时,w(x+2i)≤w(x); 当且仅当对任意的i,xi+yi≤1时,有w(x+y)≤w(x)+w(y); 以及
w(x)=w(x-1)-i+1,x≡2i(mod 2i+1),i=0,1,2,….
根据引理1有:
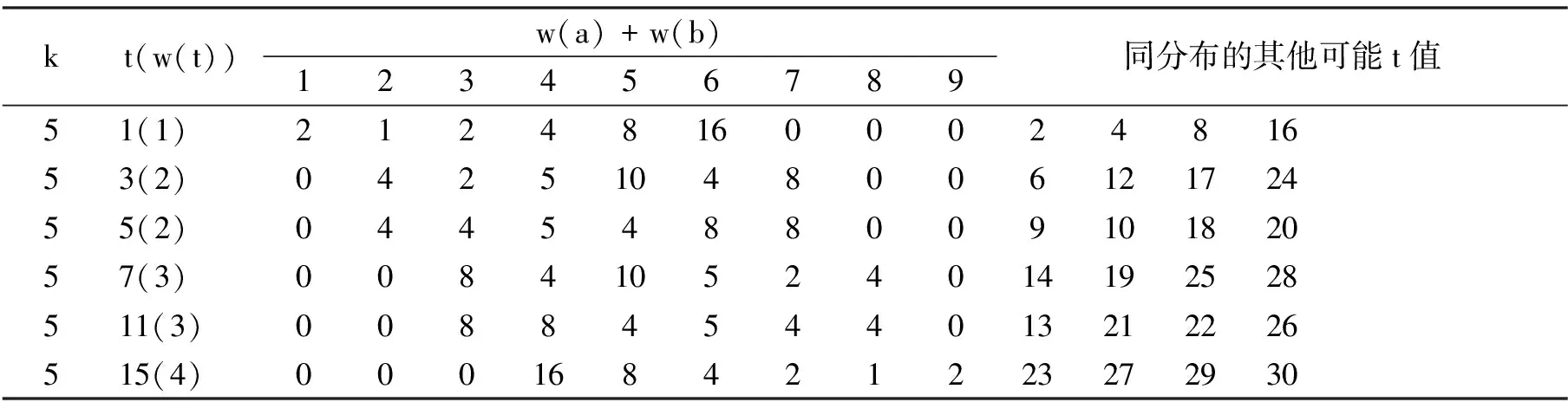
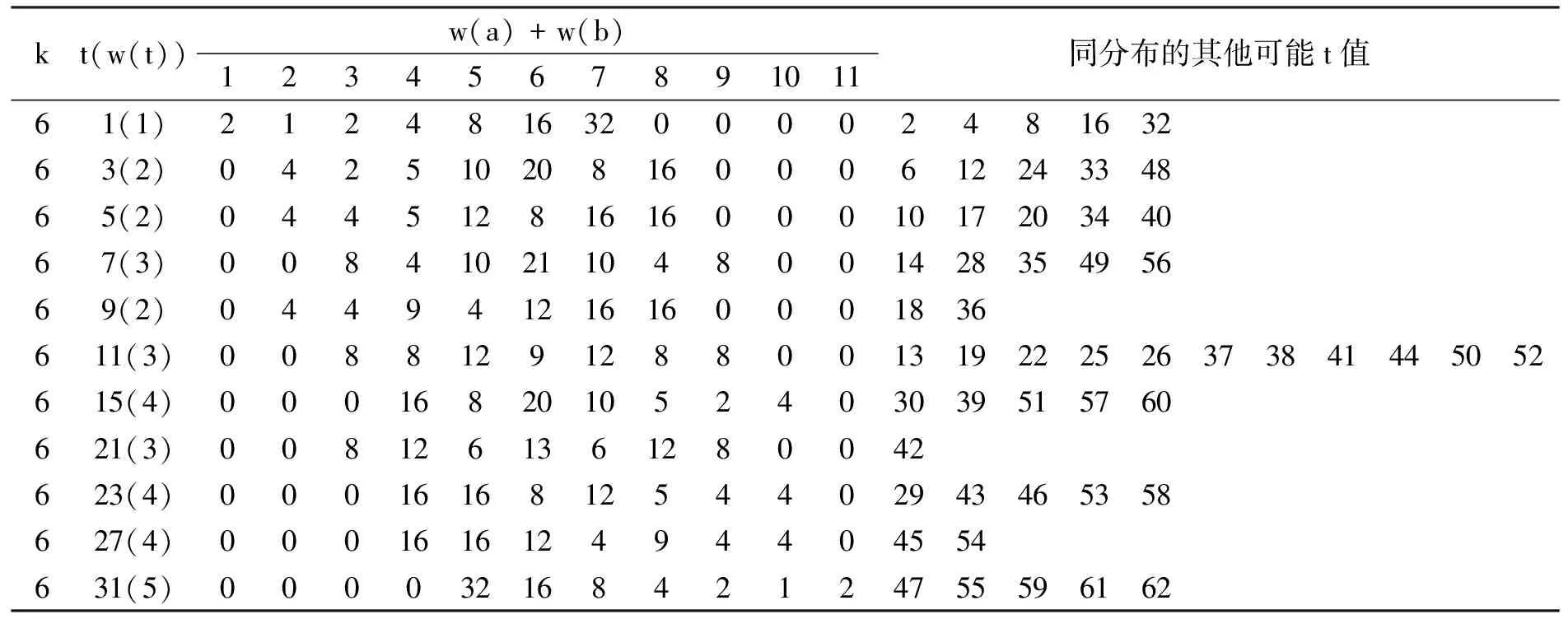
定义1(权值表构造函数) 设二进长度为k的非负整数x,y对应的和x+y的取值范围为0~2k-1,x=0或2i,i=0,1,…,k-1, 0≤y 其中1≤i≤k.由k二进表示为(x0x1…xk-1)的x旋转形成的集合为 定义3(反射)k二进表示为(x0x1…xk-1)的x的反射γ(x)定义为γ(x)=γ(x0x1…xk-1)=(xk-1xk-2…x0).显然,w(γ(x))=w(x). 本文采用C++语言,通过计算机算法实现符合条件的元素个数的计算.由于要搜寻的元素数据量呈2i(1≤i≤k)增加,算法中内存空间的分配需求较大,而计算机配置较低,因此本文只统计了二进长度较小的元素个数.算法的实现由以下两个步骤完成: 步骤1 权值表的构造.首先,根据权值表构造函数,由于非负整数x的取值设定为2i(0≤i≤k-1), 因此在循环控制变量i小于二进长度k时,总有w(x)=1.其次,初始化二进长度为k的变量x,y=1,y由二进长度为k非负整数x控制;如果y 步骤2 元素个数的分类统计.根据文献[3],把二进长度为k的非负整数x划分成两类:第一类为x=0,1,…,t,y=t-x; 第二类为x=t+v,y=2k-1-v,v=1,2,…,2k-t-2.首先,初始化循环控制变量x=0,y=t.如果x≤t, 则计算w(x)+w(y)的值.假设w(x)+w(y)的值为i, 则有St,i的元素个数#St,i=#St,i+1; 否则x=x+1,y=y-1, 循环执行得到元素个数的统计分布表. 本文选取k二进长度为5和6的数据进行分析,实验数据统计如表1和表2所示.注意到1≤t≤2k-2,w(t)是t的Hamming权,w(a)+w(b)是可能的权值,t与w(a)+w(b)所对应的数字是相应的取值个数统计. 表1 k=5的组合分布情况 表2 k=6的组合分布情况 通过对表1和表2数据的分析,可得到Tu-Deng猜想问题中的如下一些数据分布特征: 定理2(反射的数据特征) 设γ(t)=t2, 则St2,j=γ(St,j). 证明因为t2=γ(t)=γ((a+b)mod (2k-1))=(γ(a)+γ(b))mod (2k-1), 所以 γ(St,j)=γ({(a,b)|(a+b)mod (2k-1)=t且w(a)+w(b)=j})= {(γ(a),γ(b))|(γ(a)+γ(b))mod (2k-1)=γ(t)且w(γ(a))+w(γ(b))=j}. 注意到γ(t)=t2及w(γ(a))=w(a), 于是有γ(St,j)=St1,j. 参考文献: [1] Tu Ziren, Deng Yingpu. A conjecture on binary string and its application on constructing Boolean functions of optimal algebraic immunity[J/OL]. [2013-11-17]. http://eprint.iacr.org/2009/272.pdf. [2] Carlet Claude, Feng Keqin. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attacks and good nonlinearity[C]//Advances in Cryptology-ASIACRYPT 2008. Springer-Verlag, 2008:425-440. [3] Thomas W Cusick, Li Yuan, Pantelimon. On a combinatorial conjecture[J/OL]. [2013-11-17]. http://eprint.iacr.org/2009/554.pdf. [4] Zhang Xiaopeng, Deng Yulong. On a combinatorial conjecture[J]. Journal of Hunan University of Science and Engineering, 2013,34(12):58-61. [5] Flori Jean Pierre, Randriam Hugues, Cohen Gerard, et al. On a conjecture about binary strings distribution[J/OL]. [2013-11-17]. http://eprint.iacr.org/2010/170.pdf. [6] Flori Jean Pierre, Randriam Hugues. On the number of carries occurring in an addition mod 2k-1[J]. Citation Information, 2012,12(4):601-647.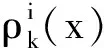
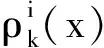
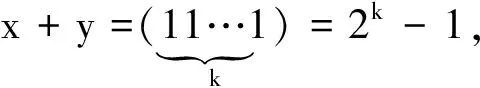
2 算法设计
3 实验数据分析