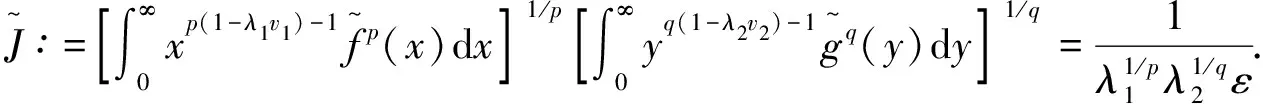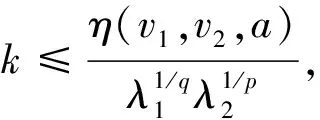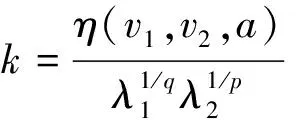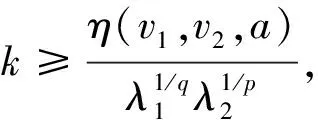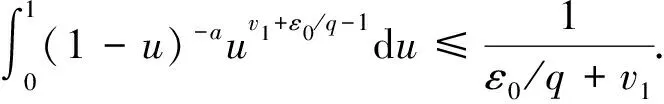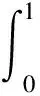一个最佳常数为Beta函数的Hilbert型积分不等式

巫伟亮

( 嘉应学院 数学学院, 广东 梅州 514011 )

1925年Hilbert[1]建立了著名的积分不等式

(1)

(2)

1 引理

(3)

证明对(3)式中的积分做变换u=xλ1/yλ2, 则有

注1由(3)式的计算过程，可得

(4)

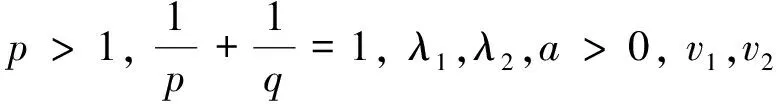
(5)

(6)

由引理1及Fubini定理[10]有

因此(5)式成立.证毕.

2 主要结果及其证明

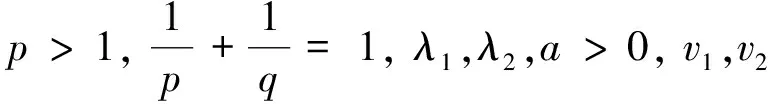
(2)为避免家族利益的纠缠，“带头人”必须从来自邻村或其他村庄的候选人中选举.本村村民不得选举本村“带头人”，本村有治村能力者，可以参加其他村“带头人”选举.

(7)

(8)

(9)

(10)

(11)

将(11)式两边p次方，可知(8)式成立，且它与(7)式等价，证毕.

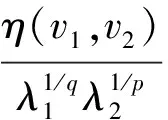
证明任意给定0<ε

(12)

由Fatou引理[10]及(12)式有

定理3在定理1所设的条件下，若把p>1改为0

(13)

注2取p=q=2,λ1=λ2=1,v1=v2=λ/2,a=λ时，由(6)式可推导出(2)式，故可知(6)式是(2)式的最佳推广式.

参考文献：

[1] Hardy G H. Note on a theorem of Hilbert concerning series of positive terms[J]. Proc London Math Soc, 1925,23(2)：XLV-XLVL.

[2] Hardy G H, Littewood J E, Polya G. Inequalities[M]. Cambridge： Cambridge University Press, 1952:226-236.

[3] Mitrinovic D S, Pecaric J, Fink A M. Inequalities Involving Functions and Their Integrals and Derivatives[M ]. Boston: Kluwer Academic Publishers, 1991:108-132.

[4] 杨必成.参量化的Hilbert不等式[J].数学学报,2006,49(5):1121-1126.

[5] Xu Jingshi. Hardy-Hilbert’s inequalities with two parameters[J]. Advancesin Mathematics, 2007,36(2):63-76.

[6] Yang Bicheng. On the norm of an integral operator and applications[J]. J Math Anal Appl, 2006,321:182-192.

[7] 巫伟亮.一个含多独立参数的新Hilbert型积分不等式及其应用[J].西北师范大学学报:自然科学版,2012,48(6):26-30.

[8] 杨必成.一个新的Hilbert 型不等式及其推广[J].吉林大学学报：理学版，2005,43(5)：580-584.

[9] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2004:12-19.

[10] 周民强.实变函数论[M].北京:北京大学出版社,2008:156-185.