伪仿射投影算法优化迭代步长的研究

郑曦, 智永锋, 张骏

(西北工业大学 自动化学院, 陕西 西安 710072)

自适应滤波技术在噪声和回波消除、均衡、波束形成中得到了广泛应用。归一化最小均方(normalized least mean square, NLMS)算法计算简单，因此获得了广泛应用[1]。但是对于高度自相关的输入信号，信号特征值相差比较大，NLMS算法表现出了收敛速度慢的特性。为了改善这一问题，提出了一些高效、快速收敛的自适应滤波算法。比如，从几何理论研究的角度，文献[2]首次提出了仿射投影(affine projection, AP)算法。通过引入输入信号方向向量的概念，建立了基于自回归模型的AP算法和滑动平均模型的正交迭代(orthogonal direction, OD)算法[3]。基于连续的输入信号相互正交将促进自适应滤波器收敛的思想，建立了一种基于正交因子的NLMS算法[4]。文献[5]建立了一种简化的AP算法，称为伪仿射投影(pseudo affine projection algorithm, PAP)算法。接着文献[6]分析了PAP算法的统计特性，研究了PAP算法的权值均方误差收敛性。

基于变步长可以促进自适应滤波的性能，文献[7]建立了一种带有指数平滑因子的AP算法。通过分析估计输出的误差信号，文献[8]获得了迭代步长的一个实时估计值，建立了一种自适应增益AP算法，接着分析了AP算法权值稳定状态的解[9]。文献[10]分析了基于回归估计误差的AP算法统计特性，接着分析了其优化迭代步长[11]。

在本论文中，通过分析PAP算法的迭代步长，利用OD算法定义的输入信号方向向量，使得在其方向的权值误差等于0，获得了PAP算法的优化迭代步长，促进了自适应滤波器的收敛性和失调量。

1 PAP算法

在自适应滤波器的系统辨识模型中，系统的输入是均值等于0的稳定信号xn。利用抽头延迟线可以把输入信号转换为输入向量xn，定义为

xn=[xnxn-1 …xn-N+1]T

(1)

由m个输入向量构成的输入矩阵Xn-1，定义为

Xn-1=[xn-1xn-2…xn-m]

(2)

系统辨识的目标是在离散的时间点n，利用最近的(m+1)个输入向量，估计一个N维的权值向量wn。文献[3]给出了用自适应滤波器实现PAP算法更新权值向量的结构，其迭代过程如下所示：

(3)

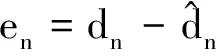
(4)

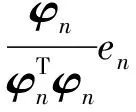
(5)

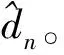
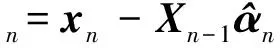
(6)

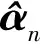
(7)

从(3)式到(7)式构成了PAP算法，下面将分析PAP算法的优化迭代步长，以促进其收敛性和失调量的性能。

2 优化迭代步长

假设存在着一个真实的N维权值向量w0。因此，相应的误差信号可以写为

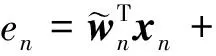
(8)

式中

(9)

εn为系统的测量噪声。为了获得PAP算法的优化迭代步长，把(5)式中的定步长μ替换成μn。基于(5)式和(9)式，可得变步长PAP算法权值误差的迭代方程

(10)

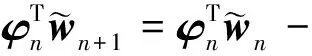
(11)

从(5)式可以看出，PAP算法的迭代方向是输入信号的方向向量φn，在(n+1)时刻,最优的迭代步长使得权值误差在输入信号方向向量的方向等于0。因此，基于(11)式，可得在n步的优化迭代步长等于

(12)

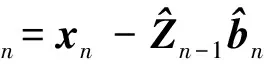
(13)

式中

(14)

定义过去k个输入信号方向向量组成的输入向量矩阵为

φn-1φn-2…φn-k]

(15)

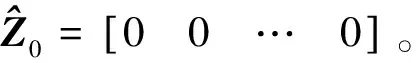
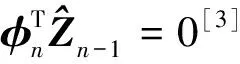
(16)

基于(15)式和(16)式,可得

; 1≤δ≤k

⋮

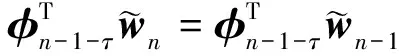
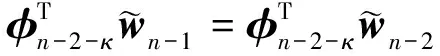
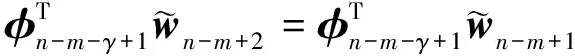
(17)

由(17)式递推可得

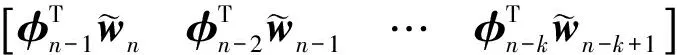
(18)

基于(11)式和(18)式,可得

(19)

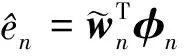
(20)

经整理,(19)式、(20)式可以重新写为

(21)

在实际系统中,系统不可避免地受到系统测量噪声的影响。基于(8)式

(22)

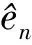
(23)

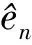
因此,可得基于优化迭代步长PAP算法的权值更新方程

(24)

(3)式、(4)式、(6)式、(7)式、(23)式和(24)式以一定的顺序构成了基于优化迭代步长的PAP算法,确保了在自适应滤波器迭代的(n+1)步,权值误差在输入信号方向向量的方向等于0。因此,所建立的算法促进了自适应滤波器的收敛速度和稳态性能。

3 仿真示例

假定自适应滤波器的初始估计权值向量w0=0,其为32维的向量。信噪比设置为60 dB,算法仿真结果的均方误差学习曲线是通过对100个相互独立的学习曲线求平均值而得,优化迭代步长μ0,opt的初始值等于1。假设自适应滤波器的真实权值向量w0具有最大熵,也就是说在各个方向具有相同大小的值。在本文中假定各个方向的幅值等于1,因此可得

w0=I

(25)

式中：I是一个所有元素等于1的32维向量。

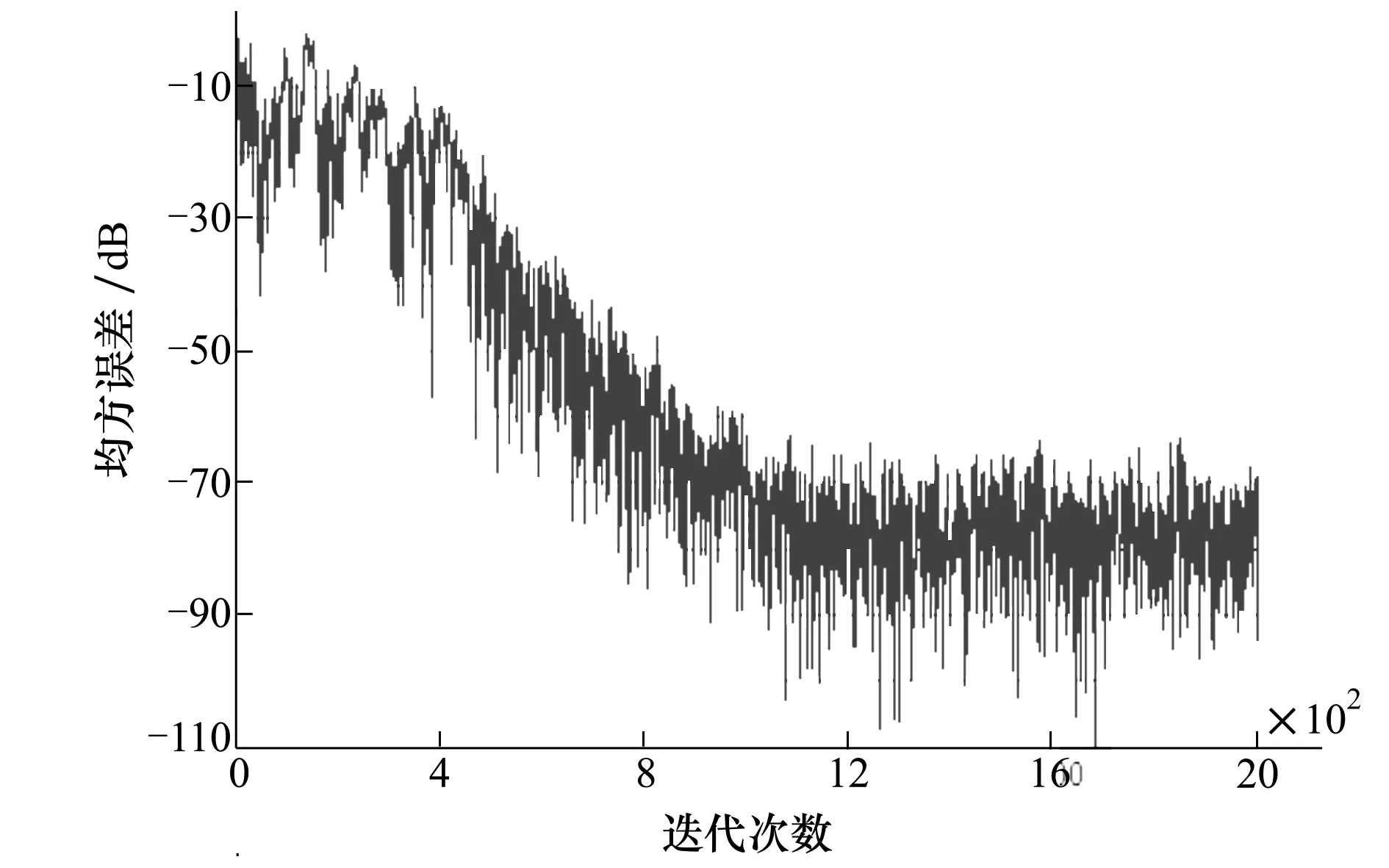
图1 输入信号是AR(1)模型时所建立算法的学习曲线

示例一输入信号是yn=-0.95yn-1+zn,其中zn为均值等于0的高斯白噪声,选择参数m和k等于2。图1给出了优化迭代步长的自适应PAP算法均方误差的学习曲线,从图中可以看出所建立算法的收敛速度比较快,稳态误差比较小。

示例二输入的信号是yn=zn+0.95zn-1-0.4zn-3-0.95yn-1,选择参数m=3和k=3。图2给出了优化迭代步长的自适应PAP算法均方误差的学习曲线,从图中可以看出所建立的算法促进了自适应滤波器的收敛速度,同时获得了比较好的稳态性能。

图2 输入信号是ARMA(1, 3)模型时所建立算法的学习曲线

4 结 论

通过分析PAP算法在输入信号方向向量上权值误差引起的估计输出误差信号，使得权值误差在输入信号方向向量的误差等于0，结合OD算法定义的输入信号方向向量，利用自回归模型和滑动平均模型可以相互近似表示的原理，获得了PAP算法的优化迭代步长。仿真结果表明：相比较于PAP算法，本文提出的算法促进了自适应滤波器的收敛性和失调量。

参考文献：

[1] Haykin S. Adaptive Filter Theory[M]. 4nd Ed. Englewood Cliffs, NJ: Prentice-Hall, 2002

[2] Ozeki K, Umeda T. An Adaptive Filtering Algorithm Using an Orthogonal Projection to an Affine Subspace and Its Properties[J]. Electronics and Communication in Japan, 1984, 67-A(5): 19-27

[3] Rupp M. A Family of Adaptive Filter Algorithms with Decorrelating Properties[J]. IEEE Trans on Signal Processing, 1998, 46(3): 771-775

[4] Sankaran S G, Louis Beex A A. Fast Generalized Affine Projection Algorithm[J]. International Journal of Adaptive Control and Signal Processing, 2000, 14(6): 623-641

[5] Bouteille F, Scalart P, Corazza M. Pseudo Affine Projection Algorithm New Solution for Adaptive Identification[C]∥Proceeding of Eurospeech, 1999, 427-430

[6] Almeida S J M D, Bermudez J C M, Bershad N J. A Stochastic Model for a Pseudo Affine Projection Algorithm[J]. IEEE Trans on Signal Processing, 2009, 57(1): 107-118

[7] Fan Y, Zhang J. Variable Step-Size Affine Projection Algorithm with Exponential Smoothing Factors[J]. Electronics Letters, 2009, 45(17): 911-912

[8] 智永锋，范蟠果，张骏，邓正宏，张怡．自适应增益APA-AG算法的研究[J]．西北工业大学学报，2011，29(3): 449-453

Zhi Yongfeng, Fan Panguo, Zhang Jun, Deng Zhenghong, Zhang Yi. A Better Affine Projection Algorithm Using Adaptive Gain[J]. Journal of Northwestern Polytechnical University, 2011, 29(3): 449-453 (in Chinese)

[9] Zhi Yongfeng, Zhang Jun, Li Yinxue．Steady-State Weights Solution to Affine Projection Algorithm[J]. Journal of Control Theory and Applications, 2012, 10(2): 259-263

[10] 智永锋，李虎雄，李茹. 一种基于回归估计误差仿射投影算法的统计特性分析[J]. 自动化学报，2013, 39(3): 244-250

Zhi Yongfeng, Li Huxiong, Li Ru. Statistical Analysis of Affine Projection Using Regressive Estimated Error Algorithm[J]. Acta Automatica Sinica, 2013, 39(3): 244-250 (in Chinese)

[11] 智永锋，郑曦，邓正宏，李茹，张骏．一种变步长AP-REE算法的研究[J]. 西北工业大学学报，2013, 31(2): 183-188

Zhi Yongfeng, Zheng Xi, Deng Zhenghong, Li Ru, Zhang Jun. A Better Variable Step-Size Affine Projection Algorithm Using Regressive Estimated Error[J]. Journal of Northwestern Polytechnical University, 2013, 31(2): 183-188 (in Chinese)