基于TMD的海上浮动风力机结构振动控制研究

贺尔铭, 胡亚琪, 张扬

(西北工业大学 航空学院, 陕西 西安 710072)

海上浮动风力机必须能够承受极端风、浪联合载荷的恶劣海洋环境而不发生结构破坏。风浪联合载荷会导致结构产生过大的振动，并且会在叶根、塔根等关键部位引起较大的疲劳载荷，这势必会增加结构的维护成本，甚至使结构产生失效破坏[1]。近年来，大多研究者基于现有风机控制系统，研究以叶片桨距角和电机扭矩的作动方式来减小浮动风力机的运动及载荷[2-3]，虽然这些方法有一定的控制效果，但仍存在叶片根部疲劳载荷过大的致命缺陷。因此基于结构主、被动控制技术来控制海上浮动风力机的过大运动和载荷是十分必要的。

将结构控制技术应用于大型风电结构控制还是一个全新的课题，目前学者大多针对陆上或固定基座的离岸风力机的TMD、TLD被动控制研究[4-5]，并未考虑浮动基座的风机结构，而且采用的都是极其简单的有限自由度的风机和支撑结构模型。Lackner等提出将TMD应用于大型海上浮动风力机的思路，初步研究了TMD在海上浮动风力机的应用[6]，但其并未进行TMD的参数优化分析，因而导致TMD对振动位移及载荷等指标的抑制率仅约为10%；另外其仅在一种环境工况下进行了仿真，得到的仿真结果具有较大局限性，因此需要在更多的典型环境工况下考察TMD的控制效果。

本文在浮动风力机动力学分析程序FAST上添加了TMD控制模块，以传统的NREL 5 MW Barge[7]式海上浮动风力机为基础，建立气动-水动-控制-TMD-结构完全耦合的浮动风力机动力学模型，进行了TMD的参数优化研究。仿真分析了有/无配置TMD的风力机结构的动态响应，并研究TMD的减振效果，为我国未来海上浮动风力机的开发提供动力学控制的技术储备。

1 海上浮动风力机模型及FAST简介

本文采用美国国家可再生能源实验室(NREL)设计的5MW Barge型浮动式风力机(如图1所示)，其机组及浮动平台的主要参数如表1、表2所示。

FAST程序是一款基于多体动力学KANE方程推导的、运用FORTRAN编程技术开发的风力机全耦合气弹-水动-伺服-弹性动力学程序，可模拟风力机的载荷及性能。本文在FAST原有自由度的基础上添加了TMD的自由度，利用此改进的FAST程序进行配置TMD风力机的结构动力学仿真。

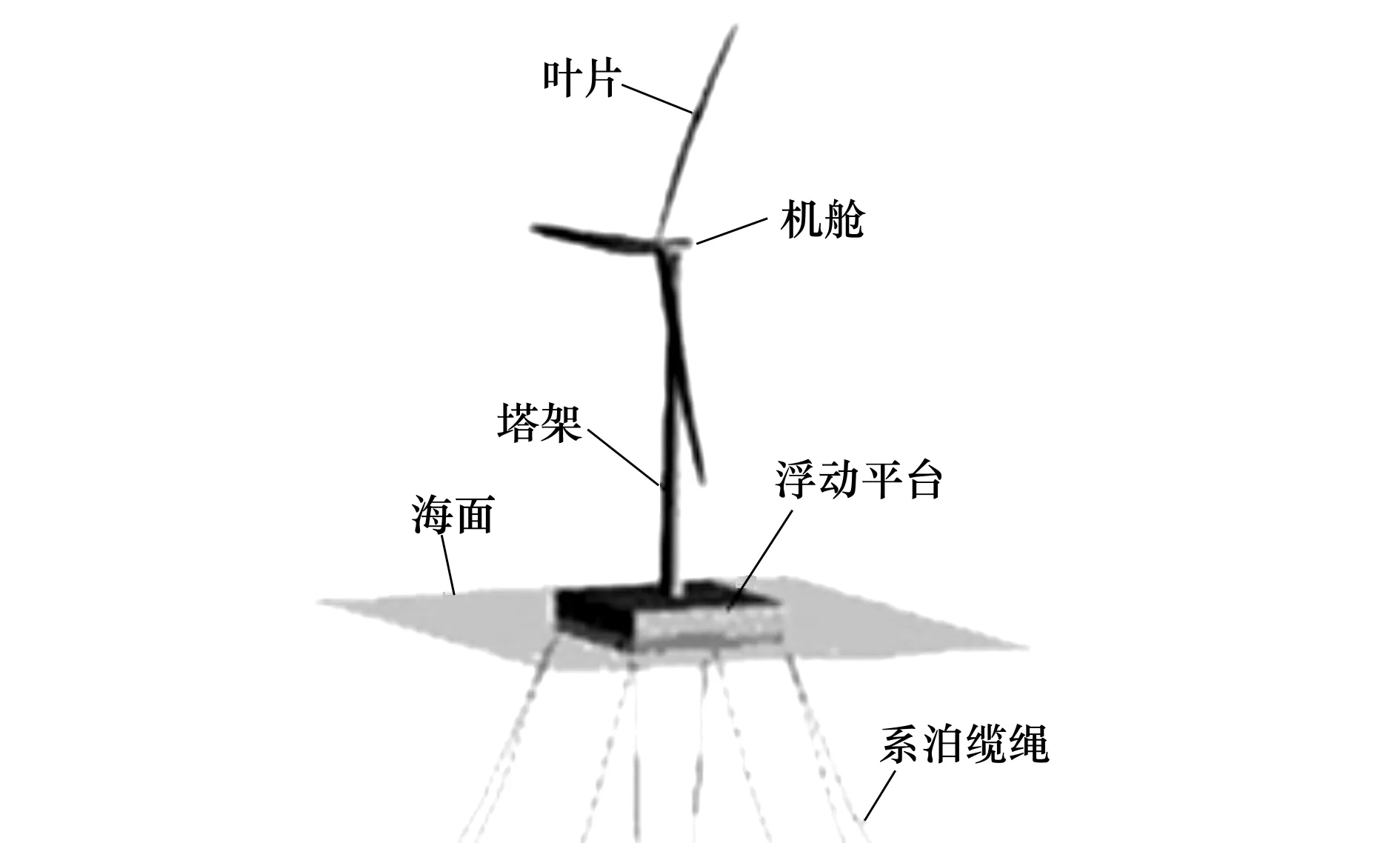
图1 Barge式浮动风力机

表1 NREL 5MW风力机主要参数

表2 Barge式浮动平台的主要参数

2 浮动风力机完全耦合动力学模型

本文建立的气动-水动-控制-TMD-结构完全耦合的浮动风力机动力学模型，包括了平台的6个平移和旋转自由度、塔架的二阶挥舞和摆振自由度、叶片的二阶挥舞方向和一阶摆振方向的自由度及被动控制TMD的2个平移自由度等共26个自由度。

2.1 风力机空气动力学模型

风力机叶轮气动载荷使用AeroDyn[8]程序进行计算，其计算方法采用动量-叶素理论(BEM)，即令2种理论(动量定理和叶素理论)推导出来的推力和转矩相等，以此得到风轮平面的轴向诱导系数a和切向诱导系数a′，其表达式为

(1)

(2)

式中：σr为半径r处圆的弦长实度，σr=Bc/2πr,B为叶片数，c为叶片弦长；φ为入流角；Cn、Ct分别为法向力系数和切向力系数。

2.2 风力机支撑结构的水动力学模型

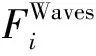
(3)

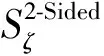
水静力学问题即为平台在静水中所受的浮力：

(4)

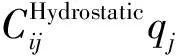
辐射问题是指在没有入射波浪的情况下，浮动平台在水中振动而产生的辐射波对平台的作用力：

(5)

式中:τ为叶片压力系数；Kij为波浪辐射延迟矩阵的(i,j)分量。

系泊缆绳拉力由式(6)计算：

(6)

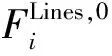
最后，综合(3)式～(6)式以及水动力附加质量的影响，可以得到支撑结构上总的水动力为：

(7)

式中:Aij为水动力附加质量矩阵的(i,j)分量。

2.3 风机控制

风机控制方法有转矩控制和联合变桨距控制。

低风速时通过调节电机的转矩使风轮按照最佳叶尖速比运行，追踪最佳风能利用系数，风能利用率较高；高风速时通过调节电机的转矩使输出功率稳定在额定功率附近。考虑转矩控制的电机转矩：

(8)

式中:Qgen为电机转矩；Pr为电机额定功率；ωgen为电机转速；ηgen为电机效率；kgen为比例常数；ωr为电机额定转速。

联合变桨距控制仅在高风速下发挥作用，通过叶片变桨限制气动力矩同样是为了稳定风机的功率输出。选择电机转速作为控制桨距角的变量，电机转速反馈信号和电机转速给定值之间的误差作为控制器的输入，PID控制器则给出桨距角参考值。

2.4 配置TMD的风力机结构动力学模型

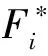
(i=1,2,…,P)

(9)

对于一个包含W个刚体，参考坐标系为Nr，质量为Mr，质量中心位置为Xr的系统，其广义驱动力和广义惯性力可由(10)式表示：

(10)

风机配置TMD系统后，在原有风机模型上耦合了2个新自由度：纵向(X向)和横向(Y向)自由度，图2为配置了纵向TMD的浮动风力机受控动力学模型，横向TMD的配置方式相同。耦合了新的自由度的风机结构动力学方程式中仅多了和TMD自由度相关的驱动力和惯性力项，其形式和(9)式、(10)式相同。

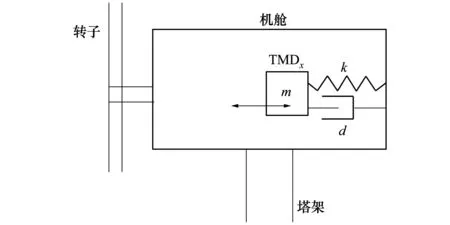
图2 配置TMDX的浮动风力机受控动力学模型

3 TMD被动控制参数优化研究

TMD是一个由质量块、弹簧和阻尼器组成的减振系统。通过调整TMD系统与风机结构的质量比μ、频率比λ及阻尼比ζd等参数，使TMD系统能吸收更多的振动能量，从而减轻风机结构的振动响应。

由于Barge型风机的载荷响应是以平台刚体俯仰和塔架一阶弯曲的联合振型为主，该振型为风机的纵向(X向)振型，故仅考虑在机舱内部沿纵向(X向)安装TMD系统，只需考虑TMDX的参数化研究。

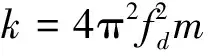
确定参数优化工况为：①整个风机系统仅保留塔架一阶弯曲自由度和平台俯仰自由度，其余自由度均关闭；②不考虑气动及水动载荷，引入初始平台俯仰角为5°的初始扰动，动态仿真模拟时长为100 s。

塔顶纵向位移TTDFA的标准差σ(TTDFA)和塔架疲劳载荷相关性很大，因此定义控制目标函数为塔顶纵向挠度标准差σ(TTDFA)的抑制率：

(11)

式中:σs、σt分别为无控结构和受控结构的塔顶纵向位移标准差。

图3为TMD不同质量比、阻尼比的组合对塔顶位移抑制率的影响。由图可知，η随μ的增大而增大，当μ<0.012 5时，η的增大幅度明显；当μ>0.012 5后，随着μ的继续增大，η的增大幅度迅速减小，故在实际应用中μ不必取得过大。ζd对η的影响规律随μ的不同而略有不同，但大体规律为先增大后减小，存在最优ζd值。当μ<0.012 5时，最优ζd值随μ的增大由0.5逐渐减小至0.35；当μ>0.012 5后，最优ζd值变化到0.55，且随μ的增大而逐渐增大。当μ=0.012 5、ζd=0.35时，η=45.7%，抑制效果已非常明显。

表3为根据上述参数研究结果确定的TMD最优技术参数；图4为按照表3最优参数配置的TMD对塔顶纵向挠度的抑制效果，可知TMD对平台俯仰运动的抑制作用明显，且在100 s内振动幅度即衰减至零。由此可知，本节TMD参数的选取合理有效；图5为TMD的行程，可知TMD的行程在-8.3～+7.5m之间，振动频率和主结构是一致的，表明TMD工作状况正常。

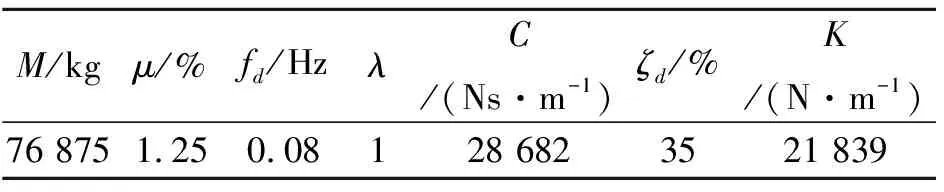
表3 Barge型风机TMD最优参数设置

图3 塔顶位移抑制率随质 图4 TMD对塔顶纵向挠度的抑制效果 图5 TMD位移时程量比和阻尼比的变化

4 设计工况

前史蒂文森气象站(位于东经0°0′，北纬61°20′)处的海洋环境条件极其恶劣，一般公认为风机如果能够胜任此处的海洋环境，则可以胜任世界上其他任何地点的海洋环境[7]。根据IEC 61400-3设计准则，本文选取此处作为风机载荷分析的环境参考点，该参考点处的海况与风速关系见文献[7]。

为了研究TMD在不同风浪环境下的控制效果，选取五种典型的风浪联合工况如表4所示，由于风机关键模态的自振频率为0.08 Hz，因此所有工况的海浪谱峰频率统一取为0.08 Hz。工况1至5分别表示风机在切入风速附近、低于额定风速附近、额定风速附近、高于额定风速附近及切出风速附近运行。

表4 设计工况

选取B级湍流强度的Kaimal风速谱，使用TurbSim[10]程序生成以表4轮毂风速为平均风速的湍流风速时程；选取Jonswap波浪谱，使用HydroDyn子程序生成以表4有效波高为平均波高的湍流波高时程。根据IEC 61400-3设计准则，本次分析针对每组工况分别选取3组随机种子，分析时间均为600 s，每一工况的统计结果以3组的平均值为准。

5 仿真结果及分析

选取以纵向载荷(叶根纵向弯矩、剪力；塔根纵向弯矩、剪力；)、纵向位移(平台纵摇角；塔顶纵向挠度)等为主要评估指标，以横向载荷(塔根横向弯矩、剪力)、横向位移(平台横摇角；塔顶横向挠度)等为次要评估指标，用以全面考察上述优化TMD在实际环境工况下的抑制效果。图6为工况4下TMD对部分主要位移评估指标的时程响应的抑制效果，图7为工况4下TMD对部分主要载荷评估指标的功率谱密度(PSD)的抑制效果；统计各评估指标在有/无TMD时的时程响应标准差并计算标准差抑制率，得到TMD对各评估指标的抑制效果，见表5。

图6a)和图6b)分别为叶尖纵向挠度、塔顶纵向挠度的时程曲线。由图可知，结构无控时，各指标的振动幅度均较大，且随着外荷载激励的不同而呈现出不同水平的振动幅度；TMD控制不但减小了各指标的振动幅度，而且使其维持在一定的振动水平。

图7a)和图7b)分别为塔根纵向弯矩、叶根纵向弯矩的PSD曲线。由图可知，塔根及叶根纵向弯矩的PSD曲线的峰值均集中在0.05～0.1 Hz之间，且无控时的最大峰值频率分别为0.078和0.073，和风机的一阶平台俯仰-塔架弯曲联合振型的自振频率及波浪载荷的谱峰频率相近；受控时塔根及叶根PSD曲线的峰值均明显减小。比较无控及受控2种情况下PSD曲线的面积，可知风机受控后塔根及叶根纵向弯矩的能量分别减小了48.3%和43.3%。

由表5可知，各载荷及位移响应的标准差抑制率在较低和较高风速下比在额定风速附近更大，说明在较低风速下TMD的附加质量更有利于结构的稳定性；而在较高风速下TMD的振动吸能性能得到了更大程度的发挥。

塔根纵向弯矩、剪力与塔顶纵向挠度三者的标准差抑制率均约为20%～50%，且根据值的分布规律可以看出它们具有正相关性；叶根纵向弯矩、剪力与叶尖纵向挠度的标准差抑制率均约为10%～40%，同样可以看出它们之间的正相关性。平台纵摇角的标准差抑制率约为35%～65%，抑制效果比塔根、叶根等指标更明显。

工况3及工况4下各横向指标的标准差抑制率较小，甚至个别指标出现了负号，相比于上述主要指标的抑制效果，这些微小的影响是可以忽略的。另外可以看出，塔根横向弯矩、剪力与塔顶横向挠度同样具有正相关性。

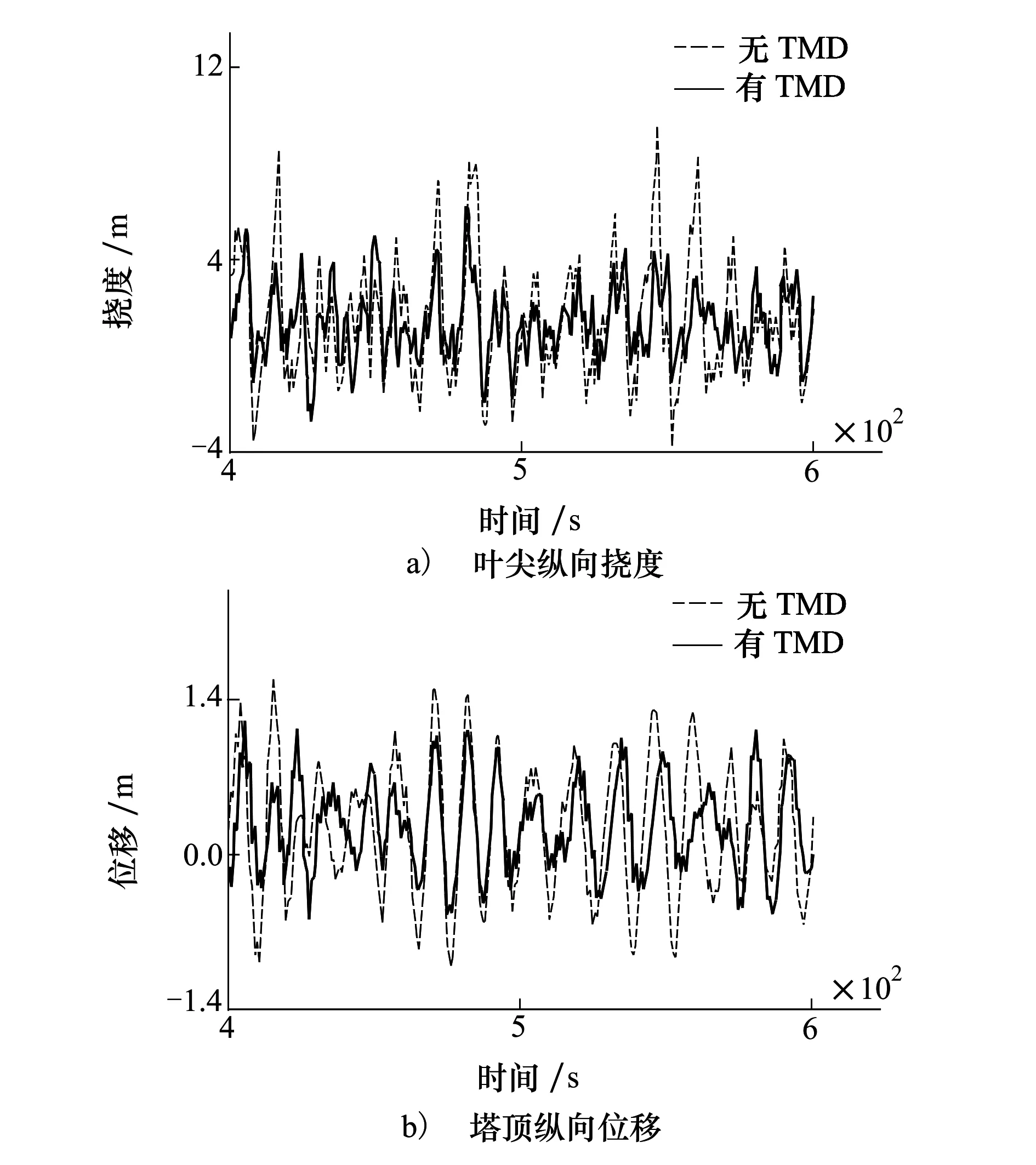
图6 工况4下TMD对主要位移指标时程的抑制效果

图7 工况4下TMD对主要载荷指标PSD的抑制效果

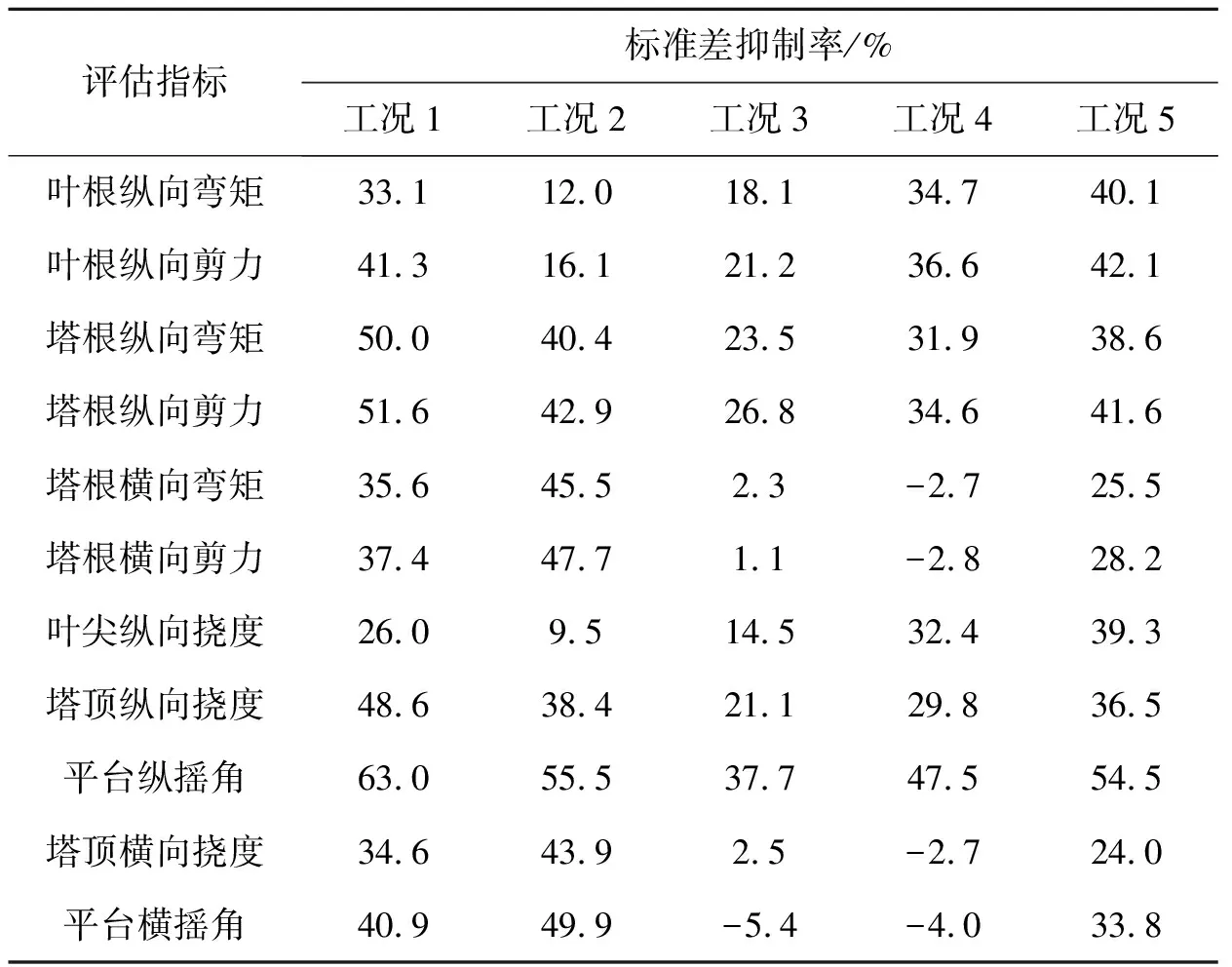
表5 TMD对各评估指标时程响应的抑制效果

6 结 论

1) 通过TMD参数优化研究，得到了Barge型海上浮动风力机沿机舱纵向布置的TMD的最优化参数配置，可使以关键模态自由振动的风机塔顶纵向挠度的标准差降低45.7%。

2) TMD对塔根纵向弯矩、剪力及塔顶纵向位移的标准差抑制率约为20%～50%；叶根纵向弯矩、剪力及叶尖纵向位移的标准差抑制率约为10%～40%。

3) 风力机各关键部位的振动载荷及位移响应的振动幅度在无TMD控制时差异较大；有TMD控制时差异较小，基本维持在一定的幅度水平上。

4) TMD在较低和较高风速下对风力机各关键部位振动响应的抑制率比在额定风速附近更大，说明在较低风速下TMD的附加质量更有利于结构的稳定性，而在较高风速下更有利于TMD振动吸能性能的发挥。

参考文献：

[1] Bossanyi E A. Individual Blade Pitch Control for Load Reduction[J]. Wind Energy, 2003,6(2): 119-128

[2] Lackner M. Controlling Platform Motions and Reducing Blade Loads for Floating Wind Turbines[J]. Wind Engineering, 2009, 33(6): 541-554

[3] Namik H, Stol K. Individual Blade Pitch Control of Floating Wind Turbines[J]. Wind Energy, 2010, 13(1):74-85

[4] Colwell S, Basu B. Tuned Liquid Column Dampers in Offshore Wind Turbines for Structural Control[J]. Engineering Structures, 2009,31(2):358-368

[5] Murtagh P J, Ghosh A, Basu B, et al. Passive Control of Wind Turbine Vibrations Including Blade/Tower Interaction and Rotationally Sampled Turbulence[J]. Wind Energy, 2008,11(4):305-317

[6] Lackner M A, Rotea M. Passive Structural Control of Offshore Wind Turbines[J]. Wind Energy, 2011,14(3):373-388

[7] Jonkman M J, Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine[R]. Golden, CO, USA: National Renewable Energy Laboratory, 2007: NREL/TP-500-41958

[8] Moriarty P J, Hansen A C. AeroDyn Theory Manual[R]. Golden, CO, USA: National Renewable Energy Laboratory, 2005: NREL/TP-500-36881

[9] Jonkman J M, and Sclavounos P D. Development of Fully Coupled Aeroelastic and Hydrodynamic Models for Offshore Wind Turbines[C]∥44th AIAA Aerospace Sciences Meeting and Exhibit, 2006

[10] Jonkman B J, Kilcher L. TurbSim User′s Guide: Version 1.06.00[R]. Golden, CO, USA: National Renewable Energy Laboratory, 2012