ANFIS 在供热管网泄漏故障诊断中的应用

段鹏飞，段兰兰，田 琦

(太原理工大学 环境科学与工程学院，山西 太原030024)

0 引言

供热管网作为城市生命线的一部分，是保证城市功能正常发挥的一个重要方面． 由于管道材质、环境、运行年代等众多因素的影响，供热管网会不可避免地发生一些故障，给城市居民生活和生产带来损失，及时发现问题并锁定故障位置可以提高供热管网运行的经济性和安全性．

供热管网中最常见的是泄漏故障，目前供热管网泄漏故障诊断的研究主要集中在基于数学模型、传感器检测和人工智能的故障诊断．基于数学模型的泄漏故障诊断［1-2］需要建立管网的精确数学模型，当受到外界因素的影响时，故障诊断的准确性会有所下降;基于传感器检测的诊断方法［3］，直接对检测信号处理，但是由于一般的城市供热管网供水温度都在90 ℃以上，所以普通的传感器很难满足要求;随着人工智能的飞速发展，自动化和智能化的泄漏故障诊断研究也不断增多．其中基于模糊理论和BP 网络的供热管网泄漏故障诊断［4-6］已经实现，但是基于模糊理论的泄漏故障诊断需要依靠专家或操作人员的经验和知识来获得模糊隶属度函数及模糊规则，难度较大;基于BP 网络的泄漏故障诊断又存在收敛速度慢、易陷入局部极值等缺陷． 为了解决这一难题，结合具有自学习功能的神经网络和可以表达模糊语言的模糊推理，笔者利用了一种自适应神经模糊推理系统(ANFIS)［7-8］对供热管网进行泄漏故障诊断．

1 供热管网ANFIS 泄漏故障诊断系统的提出

模糊理论是用数学方法处理复杂不确定问题的一门学科．若对论域U 中的任一元素x，都有一个数A(x)∈［0，1］与之对应，则称A 为U 上的模糊集，A(x)称为x 对A 的隶属度． 当x 在U 中变动时，A(x)就是一个函数，称为A 的隶属函数．隶属度A(x)越接近于1，表示x 属于A 的程度越高，A(x)越接近于0，表示x 属于A 的程度越低．用取值于区间［0，1］的隶属函数A(x)表征x 属于A 的程度高低，这样描述模糊性问题比起经典集合论更为合理．

供热管网中把节点的压力变化情况作为泄漏故障征兆，但是没有精确的压力变化度量标准来衡量管网是否发生泄漏，存在一定的模糊性．根据模糊集合论中的隶属度函数和模糊关系矩阵来描述泄漏故障与征兆之间的关系，用精确的数字来描述泄漏故障发生的中间过渡阶段的不分明性，通过建立相应的隶属度函数即可将这种模糊性转化为精确的数值描述．

传统的模糊推理系统只能依靠专家的知识经验选定模糊隶属度函数和模糊规则，而且供热管网系统一般都比较复杂，环境影响因素多［9］，仅依靠专家经验建立的模糊推理系统很难得到满意的诊断结果．因此我们把神经网络应用到模糊推理系统中，构成了自适应神经模糊推理系统(ANFIS)，发挥神经网络的自适应自学习能力，能够进行复杂的逻辑操作和非线性映射． 通过对供热管网泄漏样本数据的训练学习，自动产生并不断地修正得到最佳的模糊隶属度函数及模糊规则，避免了传统模糊推理系统易受到人的主观意识影响的缺陷，从而提高供热管网泄漏诊断系统的准确性．

2 ANFIS 简介

2．1 ANFIS 系统的结构

ANFIS 是基于Takagi-Sugeno 模型而建立的自适应神经模糊推理系统，下面用一个简单的ANFIS 系统来解释自适应神经模糊推理系统的原理．假设该系统有两个输入量x，y 和一个输出量f，且采用下列两条规则:

if x is A1and y is B1then f1=a1x+b1y+z1;

if x is A2and y is B2then f2=a2x+b2y+z2．

则对应的ANFIS 结构如图1 所示［10］．

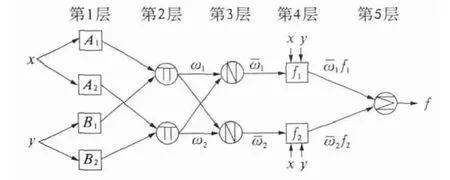
图1 ANFIS 结构图Fig．1 Architecture of ANFIS

第1 层用隶属函数将输入变量模糊化，Ai，Bi为模糊语言(如:“大”、“小”)，输出对应模糊集的隶属度，其值取决于所选择的隶属度函数μ 的类型和参数．

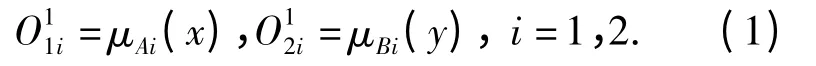
第2 层进行模糊推理，每个节点代表一个规则，将各输入变量的隶属度相乘即可得到各规则的适应度

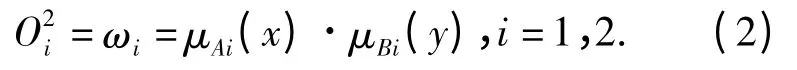
第3 层对各规则的适应度进行归一化处理，将各规则的ωi除以全部规则ω 总和即可得到各规则适应度的归一化值

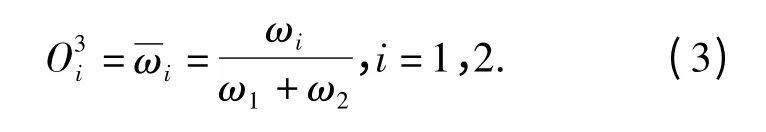
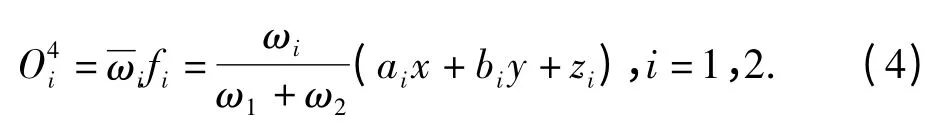
第5 层得出ANFIS 系统最后的输出值

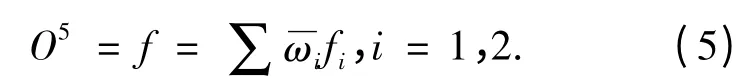
2．2 ANFIS 系统的学习算法

一般采用Jang 提出的混合算法［11-12］来对第1 层隶属函数的参数(条件参数)和第4 层线性函数的系数(结论参数)进行训练和调节，条件参数采用反向传播算法，结论参数采用线性最小二乘估计算法，这就是ANFIS 的训练学习过程． 混合算法的步骤:固定条件参数，将输入值沿图1 的网络顺序从第1 层传递到第4 层，用线性最小二乘估计算法调节结论参数，然后传递到第5 层获得输出值，与期望输出值进行比较，得到误差值后沿反向传播，调节条件参数，如此循环下去，直到误差精度达到要求得出最优的条件参数和结论参数．

3 供热管网ANFIS 泄漏故障诊断模型设计

城市供热管网的管段一般都很长，仅仅诊断出发生泄漏的管段不能满足实际要求，还需要定位具体的泄漏位置和预测泄漏量，因此供热管网ANFIS 故障模型分为两级，一级模型诊断发生泄漏的管段，二级模型进行具体的泄漏位置定位和预测泄漏量．

3．1 ANFIS 样本数据的采集

供热管网ANFIS 泄漏故障诊断的样本数据可以通过实测或者水力工况模拟来获取，但是因为实际情况的限制，通过实测采集到分布好、范围大的样本数据不太现实，一般通过水力计算数学模型模拟供热管网泄漏工况来获取样本数据．

根据基尔霍夫流量定律、基尔霍夫压降定律以及管段压力损失计算公式［13］得到供热管网水力计算模型方程组如下［14-15］．

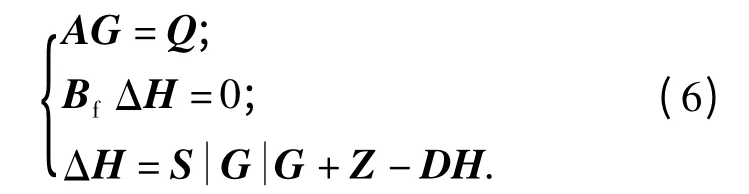
式中:A 为代表管网拓扑结构的关联矩阵;Bf为热网的基本回路矩阵;G 为管段流量列向量;Q 为各节点(参考点除外)的净流出流量的列向量;ΔH为各条管段压降的列向量;S 为对角矩阵，其对角元素为各管段的阻力特性系数Si;为管段绝对流量矩阵，其对角元素是向量G 中各元素的绝对值;Z 为各管段中两节点的位能差列向量;DH为管段水泵扬程列向量，当管段不含水泵时，该管段DH=0． 通常采用基本回路分析法(MPK 法)来求解上述方程组［15］，就可得出供热管网正常工况下管段流量和节点压力．

模拟供热管网各种泄漏工况，根据相关定义改变管网［16］的关联矩阵A、基本回路矩阵Bf和节点流量列向量Q 构成新的水力计算模型，从而求解出各种泄漏工况下管段流量和节点压力． 把各种泄漏工况的节点压力值与正常工况的节点压力进行对比就可得到各种泄漏工况的节点压力变化值，得到ANFIS 系统的学习样本数据．

3．2 一级供热管网ANFIS 泄漏故障诊断模型

假设供热管网有N 个节点(供热管网节点较多时可选取部分节点作为压力监测节点)和B 条管段．一级泄漏诊断系统针对每条管段都分别建立一个ANFIS 模型，B 个一级ANFIS 模型的结构相同:取全部节点的压力变化值作为系统输入，共N 个输入节点;取对应管段发生泄漏的概率为系统输出，共一个输出节点;将各节点的压力变化值在其取值范围内模糊分割为2 个区域，分别对应模糊语言“变化大”、“变化小”的2 个隶属度函数，一般选择高斯函数作为隶属度函数．

3．3 二级供热管网ANFIS 泄漏预测模型

针对每条管段分别建立一个二级供热管网ANFIS 泄漏预测模型． B 个二级ANFIS 模型结构相同:取对应管段2 个节点的压力变化值作为系统输入，共2 个输入节点;取对应管段发生泄漏的具体位置(泄漏点距起点的距离与此管段总长度的比值)和泄漏量作为系统输出，共2 个输出节点;将节点的压力变化值在其取值范围内模糊分割为5 个区域，分别对应模糊语言“很大”、“大”、“中”、“小”、“很小”的5 个隶属度函数，一般选择高斯函数作为隶属度函数．

4 供热管网泄漏故障诊断实例

供热管网的示意图如图2 所示，管网有10 个节点，13 条管段分别长150 m，4 个用户的设计流量均为15 m3/h，假设热源和各用户的设计阻力损失均为105Pa，正常工况下，热网循环水量为60 m3/h，水泵扬程为3 ×105Pa．

首先模拟供热管网正常工况，进行水力计算得到正常工况下各节点的压力值． 然后模拟泄漏工况，分别假定每条管段发生泄漏位置为0，0．1，0．2，0．3，0．4，0．5，0．6，0．7，0．8，0．9，泄漏量分别为总循环水量的1%，2%，3%，4%(事故补水泵一般取总循环水量的4%)．可以求得每条管段40个泄漏工况，13 条管段共520 组泄漏工况样本数据，由于篇幅限制这里不列出具体数据．

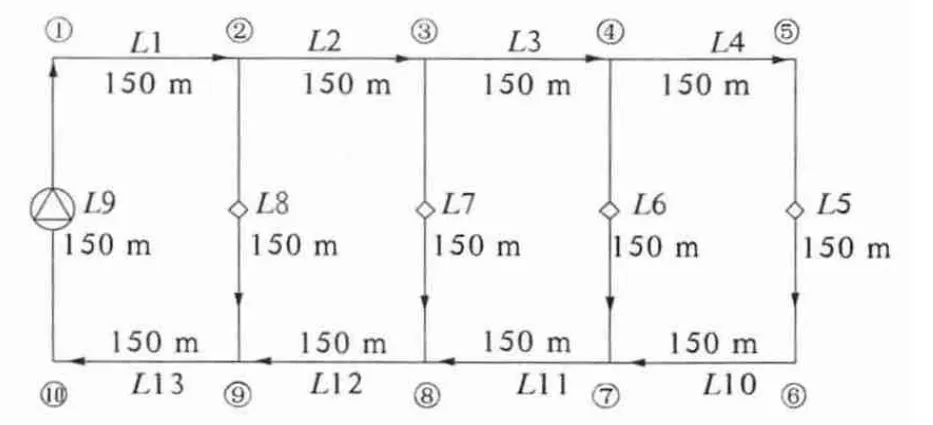
图2 供热管网系统图Fig．2 Heating network system diagram

4．1 一级ANFIS 系统泄漏故障诊断结果

以L1 管段为例，建立一级ANFIS 诊断系统，结构如图2 所示．9 个节点(节点⑩为参考节点，压力不变)压力变化值作为输入节点，L1 管段发生泄漏的概率作为输出节点，每个输入变量取2个隶属度函数，选择高斯函数作为隶属度函数，共产生521 条模糊规则．针对供热管网的特点，可以设定输出值大于等于0．5 时认为此管段发生泄漏，输出值小于0．5 时认为此管段正常．

随机选取上述520 组样本中的500 组作为训练样本，另20 组作为测试样本． 采用混合算法［11-12］对训练样本进行学习，经多次训练后得到条件参数和结论参数的全局最优解，然后将测试样本分别代入训练好的ANFIS 模型，得到测试样本的输出值见表1 的第一列．重复上述过程，得到L2 ～L13 管段一级ANFIS 模型的测试样本输出值．由表中的数据可以看出一级ANFIS 模型得到的泄漏管段发生泄漏的概率均大于0．5，因此可以准确地诊断出发生泄漏的管段．

4．2 二级ANFIS 系统泄漏故障诊断结果

以L1 管段为例，建立二级ANFIS 诊断系统．L1 管段端点节点①、②压力变化值为2 个输入节点，管段泄漏位置和泄漏量为2 个输出节点，每个输入变量取5 个隶属度函数，选择高斯函数作为隶属度函数，共产生25 条模糊规则．随机选取L1管段的40 组泄漏工况样本中的36 组作为训练样本，另4 组作为测试样本．采用混合算法对训练样本进行学习，经多次训练后得到条件参数和结论参数的全局最优解，然后将测试样本分别代入训练好的ANFIS 模型，得到测试样本的输出值． 重复上述过程，得到L2 ～L13 管段二级诊断模型的测试样本输出值．

表1 一级ANFIS 模型测试样本诊断结果Tab．1 Diagnosis results of testing sample of one－stage ANFIS model

对于同样的训练样本和测试样本，针对每条管段建立一个结构为2 -8 -1 的3 层BP 神经网络二级泄漏诊断模型． ANFIS 模型和BP 网络模型的诊断能力和精度均采用测试样本的均方根误差S 来进行评价．

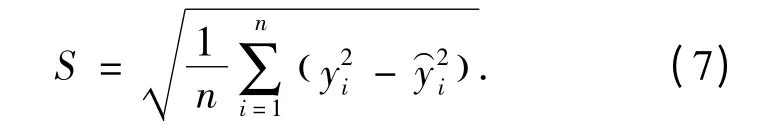
式中:n(样本数)为4;yi(诊断输出值)为ANFIS和BP 网络的测试样本输出值;y⌒i(实际值)为测试样本的实际输出值．根据上式计算出13 个ANFIS 模型和13 个BP 网络模型测试样本的均方根误差S 见表2． ANFIS 模型泄漏位置诊断结果的平均S 值为0．002 3，泄漏量诊断结果的平均S 值为0．000 2． BP 神经网络模型泄漏位置诊断结果的平均S 值为0．012 9，泄漏量诊断结果的平均S值为0．003 4，由表2 中的误差数据可以得出:传统BP 网络对于供热管网泄漏位置和泄漏量的诊断精度远低于ANFIS 系统．

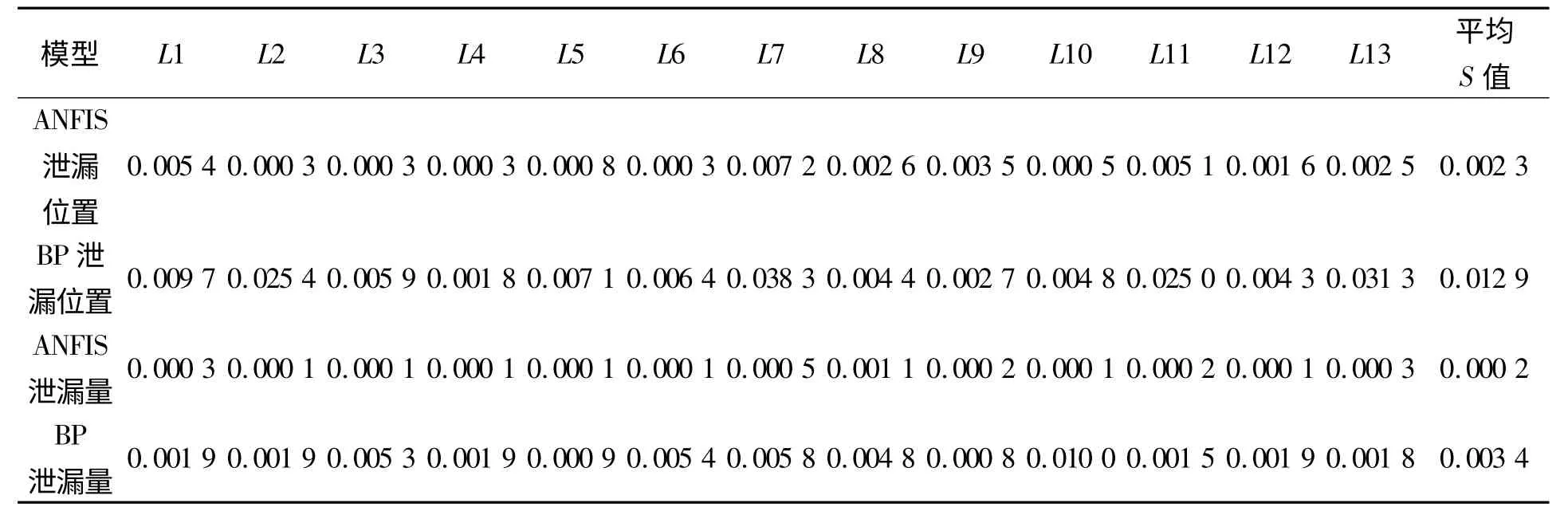
表2 ANFIS 和BP 诊断模型泄漏位置和泄漏量的均方根误差STab．2 RMSE of the leakage point and rate in the diagnosis model of ANFIS and BP

5 结论

ANFIS 集成了模糊理论和神经网络算法两者的优点，又弥补了两者应用中的不足． 本研究把ANFIS 模型应用到供热管网的泄漏故障诊断中，得到以下结论．

一级ANFIS 泄漏故障诊断模型的准确率达到了100%，预测效果良好．

在二级ANFIS 诊断模型中大部分泄漏位置和泄漏量的均方根误差S 数量级为10-4，平均均方根误差分别为0．002 3，0．000 2，而大部分BP神经网络模型中泄漏位置和泄漏量的均方跟误差数量级为10-3，平均均方根误差分别为0．012 9，0．003 4，说明ANFIS 模型诊断精度要高于传统BP 网络模型．

BP 网络泄漏位置和泄漏量诊断模型的误差起伏较大，诊断结果不稳定，可靠性差;ANFIS 诊断模型改变训练次数，多次试验发现，尽管训练次数变化，模型输出数据几乎不变，诊断结果稳定．

综上所述，ANFIS 供热管网二级泄漏故障诊断模型可以有效应用到供热管网故障智能诊断系统中．

［1］ 石兆玉，陈弘． 故障空间(FDS)法在供热管网故障诊断中的应用［J］．区域供热，1994(3):17 -19．

［2］ 杨开林，郭宗周．热力管网泄漏检测数学模型［J］．水利学报，1996，5(5):50 -56．

［3］ 姜春雷，郭远博，付兴涛，等．基于多传感器数据融合的供热管网泄漏检测技术［J］． 大庆石油学院学报，2011，35(3):91 -95．

［4］ 郑德忠，何乐，周浔，等．基于Fuzzy 理论的供热管网故障诊断系统的研究［J］． 传感技术学报，2003，12(3):367 -373．

［5］ LEI Cui-hong，ZOU Ping-hua． Application of neural network in heating network leakage fault diagnosis［J］．Journal of Southeast University (English Edition)，2010，26(2):173 -176．

［6］ 雷翠红． 供热管网泄漏故障诊断的研究［D］． 黑龙江:哈尔滨工业大学市政环境工程学院，2010．

［7］ TSAI M F，PENG Y Y，TSENG C S，et al． Modeling and estimation of state of charge for lithium-Ion batteries using ANFIS architecture［C］∥Proc．of the IEEE International Symposium on Industrial Electronics．IEEE，2012:863 -868．

［8］ YU Zhi，LIU Jian，LIU Dan，et al． Adaptive ANFISbased filter for active control of sinusoidal primary noise in nonlinear path［J］． Journal of Harbin Institute of Technology (New Series)，2011，18 (5):137-142．

［9］ 江亿．我国供热节能中的问题和解决途径［J］．暖通空调，2006，36(3):37 -41．

［10］权太范．信息融合神经网络-模糊推理理论与应用［M］．北京:国防工业出版社，2002:211 -217．

［11］周守军，赵有恩，陈明九，等． 集中供热系统水力调方法［J］．山东大学学报:工学版，2009，39(3):151-153．

［12］ LIU Min，DONG Ming-yu，WU Cheng． A new ANFIS for parameter prediction with numeric and categorical inputs［J］． IEEE Transactions on Automation Science and Engineering，2010，7(3):645 -653．

［13］孙巍． 供热管网的建模分析以及水力平衡调节［D］．北京:北京化工大学系统工程学院，2008．

［14］蒋静芝．减法聚类-ANFIS 在网络故障诊断的应用研究［J］． 计算机工程与应用，2011，47(8):76-78．

［15］王思莹，邹平华，周志刚，等． 基于图论的直接连接热水供热系统热力工况计算模型［J］． 暖通空调，2011，41(8):106 -109．

［16］周游，李嘉．多热源环状热网水力计算研究［J］． 煤气与热力，2011，31(7):A19 -A22．