考虑分区最小骨干网架的抗灾型输电网规划

马建勃,聂宏展,赵 莹,赵 丹

(东北电力大学,吉林 吉林 132012)

重大自然灾害是危害输电网安全运行的重要因素之一。按照国办发[2008]20号“国务院批转发展改革委电监会‘关于加强电力系统抗灾能力建设若干意见的通知’”文件,针对降低自然灾害对输电网的影响,提出了“普遍提高,重点加强”的差异化设计思路。电网输电线路差异化设计的目的就是要建立一个能够在自然灾害下保证刚性负荷持续可靠供电的骨干网架。差异化的设计标准使得工程投资大幅增加,但是提高线路的抗自然灾害标准,能够使电网在受到灾害的情况下,巩固电网网架,提高电网的稳定性,降低灾害对输电网造成的损害,并降低了抢修和重建的二次投资费用。

文献 [1]、文献 [2]对冰灾进行分析调研,提出了从电网规划、设计、运行等角度加强电网抗灾能力建设,但未进行定量分析。文献[3]从冰雪灾害下我国电网安全运行所面临的问题出发,指出了在冰雪灾害条件下我国电网安全运行需要加强研究的几个关键问题。文献[4]提出了考虑典型自然灾害场景约束的抗灾型电网规划方法,从满足抗灾要求角度给出了完善相关电网规划技术规程的建议。本文建立了分区最小骨干网架的抗灾型输电网二层规划模型[5],采用人工鱼群算法[6-8]对该模型求解,通过方案比较验证了模型的有效性和合理性。

1 抗灾型输电网规划模型

1．1 模型建立

抗灾型输电网规划与传统输电网规划[9-10]在建模上有 2点不同：

a．抗灾型输电网规划要求重要线路的差异化投资与正常规划线路投资整体最优,对于已建线路是否需要进行差异化改造也需要考虑,因此决策变量和总投资将会比传统的输电网规划大大增加;

b．抗灾型输电网既能满足正常情况下的所有负荷供电,又能满足自然灾害下,刚性负荷的持续可靠供电。

基于以上所述,本文建立了基于二层规划的抗灾型输电网规划模型。

1．2 上层模型

上层为分区最小骨干网模型。骨干网分区的目的是在保证刚性负荷可靠供电的前提下尽可能减少差异化设计线路数量,最大限度节约投资费用。这就可能使系统成为几个相互独立的区域。目标函数如下：

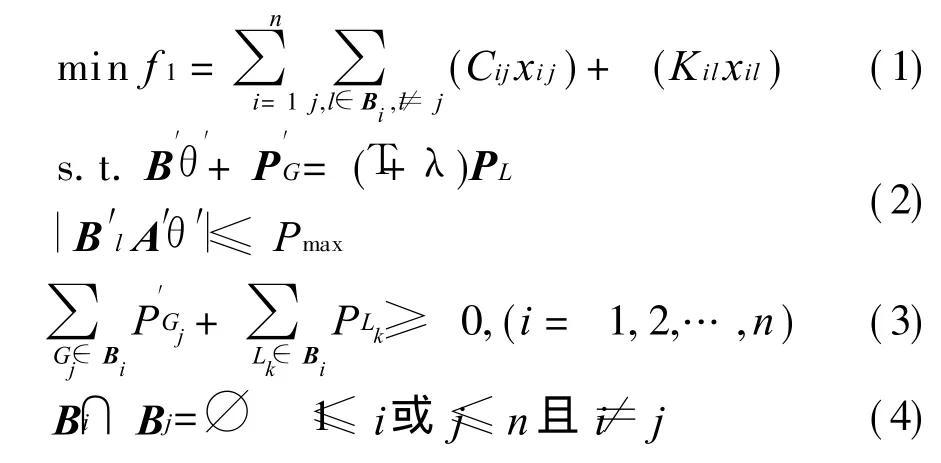
式中：Bi是分区后的第 i个连通区;分区n个;Cij、Kil分别是第i分区支路 j中扩建一回新建差异化线路的投资费用和支路l改造成一回差异化线路的投资费用;xj为支路 j的扩建回路数;xl为改造回路数;B′为系统的节点导纳阵;θ′为系统的节点电压相角;PL为系统负荷;B′L为各支路组成的对角阵;A′为系统关联矩阵;T为比重因子,即负荷节点中刚性负荷占此节点总负荷的比重,根据相关文献一般T取 0．3;λ为分区因子,若没有,则所求方案满足分别为电源节点数和刚性负荷节点数),对最优方案断线分区后,某些区将不再满足区内功率约束条件 ,即引入分区因子λ后,各电源节点出力将比未引入分区因子的值大,可以确保分区后所有区域都满足功率约束条件。P′Gj是Bi区中的电源节点,为一个正实数,表示通过节点i向电网输出的功率;PLk是和 P′Gj属于同一个区的负荷节点,是个负实数,表示通过节点k从电网吸收功率。

1．3 下层模型

为既能在自然灾害下能够保证刚性负荷供电,又满足正常情况下的所有负荷供电的要求,建立下层数学模型如下：l

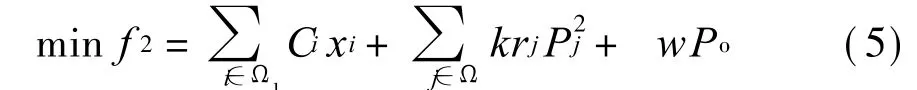
约束条件：

式中：Ci支路i扩建一回新建线路的投资费用;xi是对应支路的回路数;rj是支路j的电阻值;Pj是支路j上的传输功率;Po是总的过负荷量;k是常数;w是过负荷的惩罚系数;Ω1是新建线路集,Ω包括新建线路,新建差异化线路,已建线路和改造成差异化线路的集合。

2 基于最短电气距离的最小骨干网分区

2．1 有权电力网路的建立

电力系统是非常典型的复杂网络,它是由节点以及节点之间的边构成,其中节点为系统中的元素,边表示各元素之间的相互联系。如果所有的边都有相应的权值,那么就是有权网络。有权网络建可以完整地描述各节点间的联系。根据电力网路的实际特征,用线路的阻抗参数Xl表示相应边l的权值,做一下假设：

a．将发电机节点、变电站节点以及负荷节点作为网络的节点,输电线路和变压器作为边;

b．如果系统中含有同杆双回线或者多回线,那么将它们进行合并,看成一条边,此边的权值为等值后的线路阻抗。

那么对于一个节点数是n,m条边的电力网路,其有权网路的数学模型可以用图g以及边权连接矩阵Wg进行如下描述：

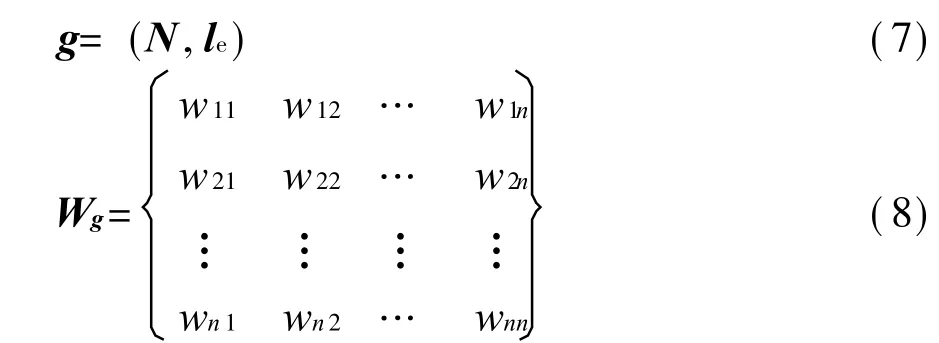
式中：N是电力网路中的所有发电机节点、变电站节点以及负荷节点的集合,N={n1,n2,… ,nn};le是电力网路中有权边的集合,le={le1,le2,… ,lem}。

边权邻接矩阵Wg的矩阵元素wij为：

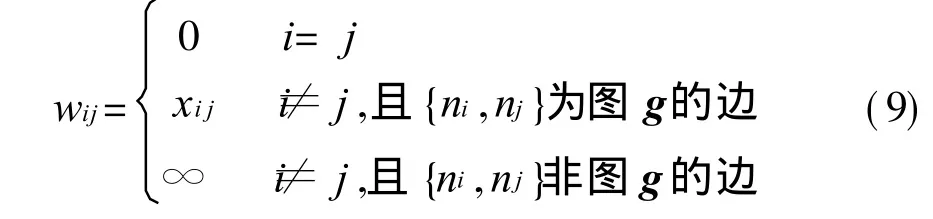
式中：xi j为节点i、j之间的边的阻抗值。

2．2 节点间最短电气距离

对于带权图g,如果p是从节点u到节点v之间的全部路径中距离最短的一条路径,那么p称作从u到v的最短路径,此路径所经过的所有边的权值和le称为从u到v的最短距离[11]。

电气距离的大小在一定程度上反映了电力网路中不同节点之间的电气强弱联系。其值越大,说明这两个节点在网路中的联系越弱;反之则越强。因此,搜寻节点间的最短电气距离,其本质上就是搜寻此节点间电气联系最强的那条路径。针对矩阵Wg,采用 Floyd算法[12]求出所有节点对之间的最短电气距离矩阵。

D= [di j](i或 j=1,2,… ,n)。

2．3 求解最小骨干网分区

通过对输电网进行合理的数学建模,将求解分区最小骨干网转化为数学优化问题。具体求解流程如下。

步骤1：通过人工鱼群算法求取在只含刚性负荷时的最优规划方案。

步骤2：根据步骤1)获得的规划方案形成相应的边权邻接矩阵Wg,对Wg矩阵使用Floyd算法求出最短电气距离矩阵 D=[dij](i、j=1,2,… ,n)。

步骤 3：对每个电源节点,若存在线路lk(lk为步骤 1规划方案中的第k条线路),使电源节点和刚性负荷节点直接相连,并且满足P′Gi+TjPLj≥0,则修改电源节点数值 ,即P′Gi=P′Gi+TjPLj,,将线路 lk记录在分区矩阵B中,然后搜索与 j相连的刚性负荷节点的线路,如果满足P′Gl+TkPLk≥0,则修改电源节点数值 ,即 P′Gi=P′Gi+TkPLk,将此线路记录在分区矩阵 B中,然后搜索与k相连的刚性负荷节点的线路,直到存在线路ll使得P′Gi+TlPLl＜0,此时不进行电源节点数值的修改但将-ll记录在分区矩阵中(记录-ll是为了区间互联合并,在步骤 4中将予以说明)。B为n×(m+1)阶阵(n,m分别为电源节点的最大编号和刚性负荷节点的最大编号),其元素为：

步骤 4：查看分区矩阵中每一列的元素,如果相同列(假设为第i列)中有s(s＞ 1)个大于零元素,则说明第i个刚性负荷节点与s个电源节点直接相连,各电源节点的编号为第i列中非零的行数,查询最短电气距离矩阵D,保留分区矩阵B第i列中电气距离最短的线路所在的行,对第i列中其他大于零的元素全部变为零,且相对应的行的第m+1列进行P′Gi=P′Gi-TjPLj修改。如果相同列 (假设为第 k列 )中有s(s＞ 1)个小于零元素,则说明第k个刚性负荷节点与s个电源节点直接相连,查询最短电气距离矩阵D,如果存在q(q≤s)个最短电气距离之和最小且使得 (∑i∈qP′Gi-TkPLk)≥ 0,将 Bij(i∈ q,j=k)中负值改为正值,其他变为零,并计入联络矩阵R中,R为n×n阶阵(n为电源节点最大编号),然后跳入步骤5。

步骤 5：查找有无孤立的刚性负荷节点,如果没有,则结束,如果有转入步骤 6。

步骤 6：修改分区因子λ,带入步骤 1重新执行。

3 IEEE 18节点系统算例

采用典型的 IEEE 18节点系统进行算例分析,分别取T=0．3,λ=0,T=0．3,λ=0．05和T=0．3,λ=0．08进行分区计算,分区结果如表1至表3所示。

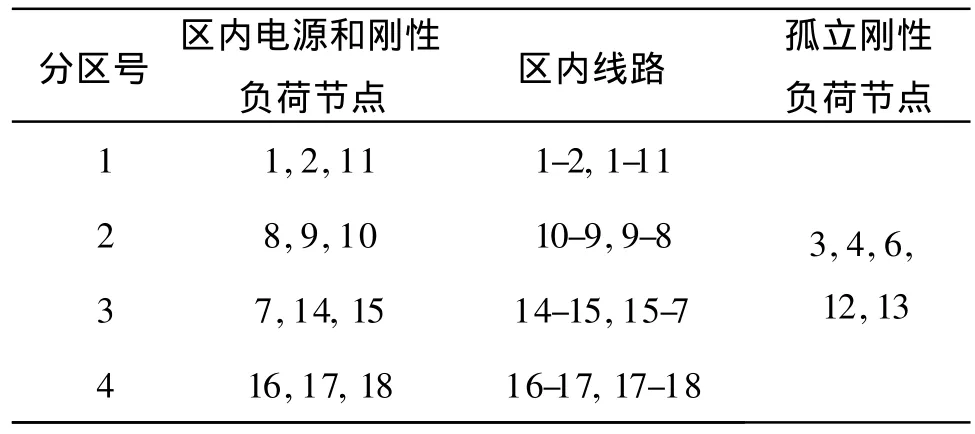
表1 α=0．3,λ=0时的分区最小骨干网架

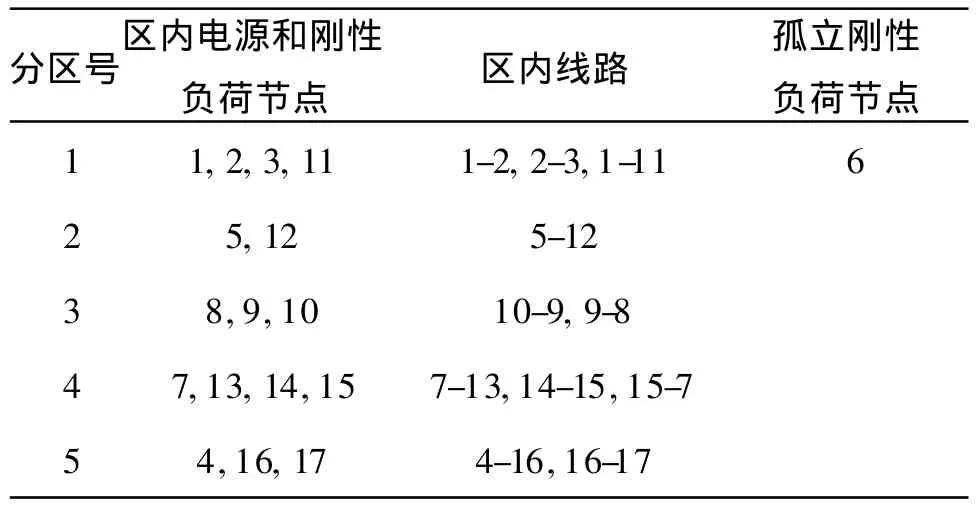
表2 α=0．3,λ=0．05时的分区最小骨干网架

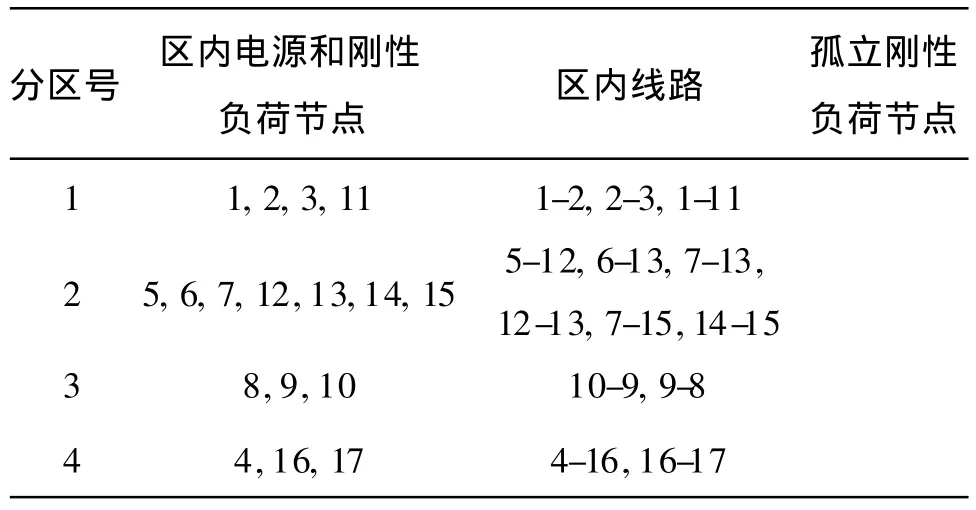
表3 α=0．3,λ=0．08时的分区最小骨干网架

以满足所有刚性负荷供电时求取的分区最小骨干网架的差异化线路和改造线路作为下层规划模型的参数得到IEEE 18节点的基于分区最小骨干网架的抗灾型规划方案如图 1所示。

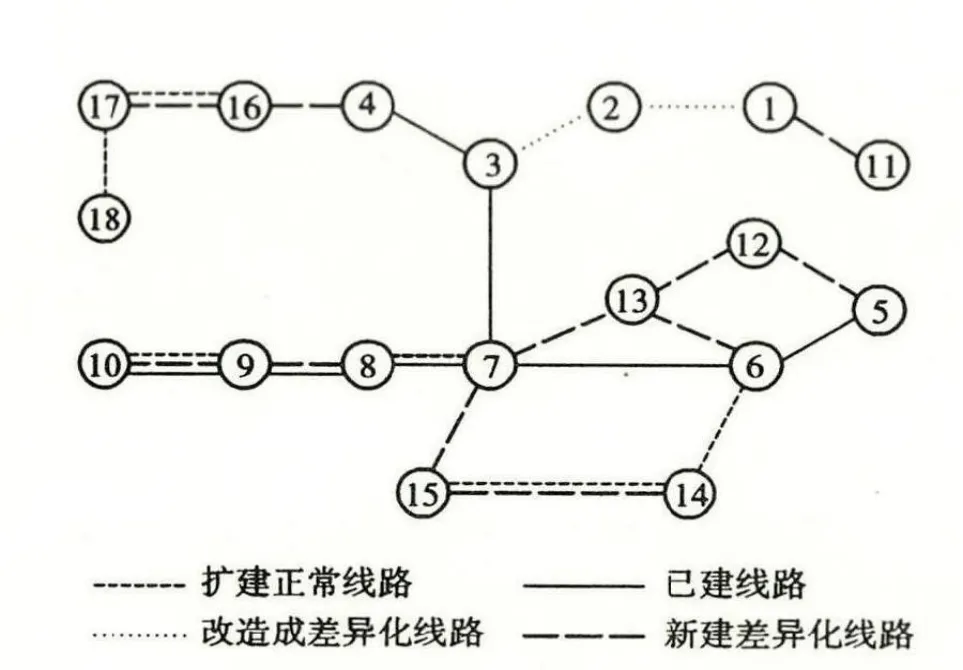
图1 考虑分区最小骨干网架的抗灾型规划方案

灾害场景下,由于分区最小骨干网架的作用,全网解列成4个区域,节点 2和 11通过差异化线路供应节点3和节点1的刚性负荷;节点5和14通过差异化线路供应节点 6、7、12、13和 15的刚性负荷;节点10通过差异化线路供应节点 9和节点 8的刚性负荷;节点16通过差异化线路供应节点4和节点17的刚性负荷。

4 方案比较

表4为本文差异化规划方案与未考虑差异化时的正常规划方案的比较,其中差异化线路的投资是正常线路的 1．8倍[13],改造成差异化线路的投资假设也为正常线路的 1．8倍,灾害下所有非差异化线路全部损害,需重新架线。

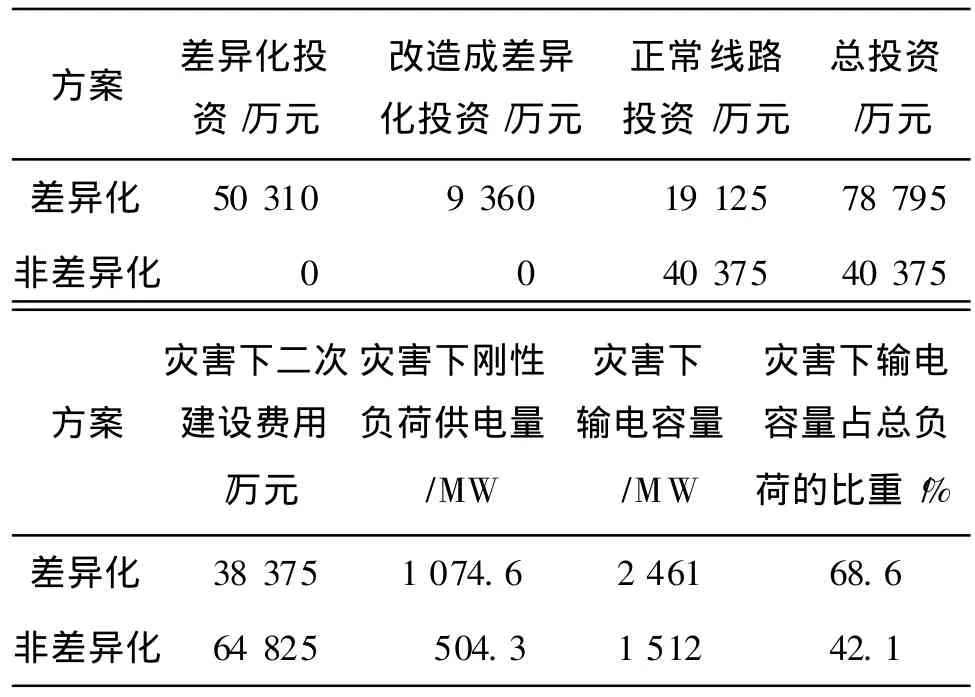
表4 差异化规划方案与未考虑差异化时的正常规划方案的比较

差异化抗灾方案虽然比非差异化方案的投资费用(总投资费用加上灾害下二次建设费用)增加11．38%,但差异化规划方案满足所有刚性负荷(1074．6 MW)供电,非差异化方案只能供给504．3 MW,并且在输电容量上比非差异化方案多950 MW。当考虑到刚性负荷造成的社会价值,差异化规划方案将优于非差异化方案。以上分析表明,差异化规划方案可以满足正常情况下电网对经济性、可靠性的要求以及在发生重大自然灾害情况下刚性负荷的供电保障要求,表明了该模型可适用于抗灾型规划中。

5 结论

自然灾害对输电网造成了严重影响,传统规划模型已不能满足输电网在抗灾方面的要求,本文通过深入研究抗灾型电网规划问题建模特殊性的基础上,与传统电网规划模型相结合,建立了最小分区骨干网架的二层抗灾规划模型。在上层模型中通过改变分区因子,结合图论求取的最短电气距离获得分区最小骨干网,使得在自然灾害下满足输电网对刚性负荷的持续可靠供电。上层模型将分区最小骨干网传递给下层模型,通过下层模型求解出正常情况下满足所有负荷供电的方案,从而得到满足抗灾的输电网规划方案。针对 IEEE18节点系统从投资费用、灾害下二次建设费用、灾害下刚性负荷供电量以及灾害下输电容量等方面对比分析差异化抗灾方案和非差异化方案,结果表明本文建立的模型可用于抗灾规划,能为规划人员带来一定能的参考价值。

[1]胡毅．电网大面积冰灾分析及对策探讨[J]．高电压技术 ,2008,34(2)：215-219．

[2]黄强,王家红,欧名勇．2005年湖南电网冰灾事故分析及其应对措施 [J]．电网技术,2005,29(24)：16-19．

[3]李成榕,吕玉珍,崔翔,等．冰雪灾害条件下我国电网安全运行面临的问题 [J]．电网技术,2008,32(4)：14-22．

[4]徐国新,夏清,康重庆．抗灾型电网规划模式与模型[J]．电力系统自动化 ,2010,34(3)：17-21．

[5]范宏,程浩忠,金华征,等．考虑经济性可靠性的输电网二层规划模型及混合算法 [J]．中国电机工程学报,2008,28(16)：1-7．

[6]聂宏展,吕盼,乔怡,等．基于人工鱼群算法的输电网络规划 [J]．电工电能新技术,2008,27(2)：11-15．

[7]聂宏展,乔怡,吕盼,等．基于混合人工鱼群算法在输电网规划 [J]．电网技术,2009,33(2)：78-83．

[8]吴杰,刘健,卢志刚,等．适用于输电网网架规划的人工鱼群算法 [J]．电网技术,2007,31(18)：63-67．

[9]程浩忠,高赐威,马则良,等．多目标电网规划的一般最优化模型 [J]．上海交通大学学报,2004,38(8)：1229-1232．

[10]Edson L S,Hugo A G,Jorge M A．Transmission network expansion planning under an improved genetic algorithm[J]．IEEE Transactions on Power Systems,2000,15(3)：1168-1175．

[11]曹一家,陈晓刚,孙可．基于复杂网络理论的大型电力系统脆弱线路辨识 [J]．电力自动化设备,2006,26(12)：1-5．

[12]李运坤,吕飞鹏,蒋科,等．基于最短电气距离的运行方式组合方法 [J]．电力系统保护与控制,2010,38(15)：24-27．

[13]徐国新,夏清,康重庆．电网抗灾投资决策方法研究[J]．电力自动化设备 ,2010,30(2)：22-27．