隐Makrov机制转移与随机时间水平下的多期资产配置*

张 玲，曾 燕

(1.广东金融学院经济贸易系，广东 广州 510521；2. 中山大学岭南学院，广东 广州 510275)

自Markowitz[1]开创性地提出均值-方差模型以来，应用定量分析方法研究金融问题已成为了现代金融经济学的研究热点。囿于Markowitz均值-方差模型的单阶段静态特点，为更符合金融市场实际，后来很多学者致力于动态投资组合选择问题的研究。Merton[2]假定股票收益服从几何布朗运动，研究了CRRA效用下的连续时间动态投资组合选择问题。Li等[3]，Zhou等[4]分别将Markowitz的静态均值-方差模型拓展到了多阶段和连续时间情形。随后，Lim等[5]，Zhu等[6]和Leippold等[7]分别就具有随机参数、破产风险控制和负债等现实约束时的动态均值-方差投资组合选择问题进行了研究。Basak等[8]，Björk等[9]进一步研究了均值-方差投资组合选择问题的时间一致性策略。

现实金融市场中，各种市场信息和状态都会对资产收益产生显著影响。考虑存在市场状态风险下的投资组合选择问题成为了近年研究的热点之一，其中Markov 机制转移模型常用来刻画金融市场状态的演化过程。Markov机制转移模型最先由Hamilton[10]提出，其典型的特点是用离散或连续时间有限状态Markov链刻画金融市场状态的演化过程。过去十多年中，各类研究表明Markov链不仅能非常好地拟合金融时间序列数据，还能很好地描述金融市场的动态变化。因此，Markov机制转移模型也被大量应用到了投资组合选择问题的研究中。在市场状态完全可观测的金融市场中，Zhou等[11]最先研究了Markov机制转移下的连续时间均值-方差最优投资组合选择问题。Çakmak等[12]提出了Markov机制转移市场中的多阶段均值-方差模型，并利用动态规划方法以及文[3]提出的嵌入法，求得了最优策略和有效边界。Costa等[13]将文[12]的模型推广到了更一般的情况。Wu等[14]考虑了随机收入和机制转移对最优策略的影响。

上述文献中，Markov链的状态均假定为完全可观测的，且状态转移矩阵是定常的。事实上，金融市场也存在一些不能直接观测的状态，但其释放出一些信息融合在可观测的状态中。也就是说，投资者在进入市场的时候并不能观测到所有的市场状态，但随着时间推移，投资者观测到的信息不断累积，投资者可依据其决策时刻掌握的所有信息做出最优的决策。隐Markov机制转移模型通常用来刻画这种不可观测市场状态的变化过程。Honda[15]研究了隐Markov机制转移市场下的最优投资消费问题，并发现长期投资者和短期投资者的投资策略存在显著差异。在隐Markov机制转移市场中，Bäuerle等[16]采用随机滤波和动态规划方法得到了对数效用和幂效用下最优投资策略的解析解。Haussmann等[17]研究了投资者只能观测到风险资产价格的终端财富效用最大化问题。Bensoussan等[18]考虑了通货膨胀对于最优投资消费策略的影响。Elliott等[19]利用随机滤波方法和随机最大值原理，得到了隐Markov机制转移市场中的最优均值-方差投资组合策略。Çanakolu等[20]研究了HARA效用下的多阶段投资组合选择问题。Bae等[21]利用情景生成法构建了均值-方差随机资产配置模型。

稍微遗憾的是，上述Markov机制转移市场下最优投资组合选择问题的研究中，投资者结束投资活动退出市场的时间均假设为固定的。但现实中，投资活动会受到许多随机因素的影响。如果市场环境的变化导致投资信心不足，投资者可能会在中途结束投资活动退出市场。不确定退出时间下的最优资产组合问题最早可以追溯到Yaari[22]，其首先研究了死亡时间不确定时整个生命周期内的投资消费问题。近年来，有关不确定退出时间问题的研究越来越多。Karatzas等[23]解决了退出时间为资产价格滤子停时下的动态投资问题。Liu等[24]研究了退出时间服从指数分布时的投资组合选择问题。郭文旌等[25]构建了不确定退出时间下的动态均值-方差模型。Blanchet-Scalliet等[26]研究了退出时间独立于市场状态和资产价格的连续时间投资组合选择问题。Yi 等[27]考虑了不确定退出时间对最优资产负债管理策略的影响。在资产收益序列相关的金融市场中，Zhang 等[28]得到了退出时间不确定时最优资产组合策略的解析表达式。Zeng等[29]考虑了效用函数依赖于市场状态时不确定退出时间对最优投资-消费策略的影响。Wu[30]假定退出时间是依赖于市场状态，且市场状态完全可观测。Wu等[31]和Yao等[32]综合考虑了Markov机制转移市场中不确定退出时间和内生负债对于动态资产组合策略的影响，但其仅考虑了市场状态完全可观测的情况。上面所提及的研究中，并没有同时考虑市场状态部分可观测且不确定的退出时间依赖于市场状态的情况。

综上，我们发现在信息部分可观测的金融市场中分析依赖于市场状态的不确定退出时间对最优投资策略的影响具有重要的现实意义，也可拓展已有的研究成果。为此，本文拟在状态部分可观测的金融市场中，探讨不确定退出时间下的多期均值-方差投资组合选择问题。不同于已有研究的是：① 本文假定同时存在可观测和不可观测的市场状态，并利用隐Markov链刻画不可观测市场状态的变化过程；② 无风险资产的收益依赖于可观测的市场状态，风险资产的收益同时依赖于可观测和不可观测市场状态；③ 状态转移矩阵随着时间变化而变化。

1 模 型

假定金融市场中存在一个风险资产和一个无风险资产，投资者在时刻0以初始财富x进入市场，计划进行为期T个阶段的投资活动，则计划投资结束时间为T，其中第k个阶段指时间区间[k-1,k)，k=1,2,…,T。假设金融市场中存在投资者可观测的市场状态，也存在不可观测的市场状态。在每个阶段初，投资者依据观测到的市场状态信息做出投资决策。

1.1 市场状态

1.2 金融市场与财富过程

(1)

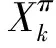
Pr{T∧τ=k|Ok=s}=

Pr{τ=k|Ok=s}=pk(s)，k=1,…,T

这里，假定p0(s)=0。

在期望投资收益目标d下，投资者在时刻0以初始财富x进入市场。此时市场上所有可观测和不可观测状态为(O0,U0)，但投资者只能得到O0的信息。投资者希望根据此时掌握的信息O0寻找到最优的投资策略，使得投资结束时投资风险最小， 即求解以下均值-方差优化问题

2 充分统计量

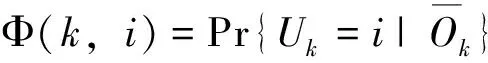
(2)

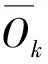
(3)

确定。现实投资实践中，投资者通常利用时刻0掌握的市场信息分析推断得到Φs(0)。

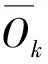
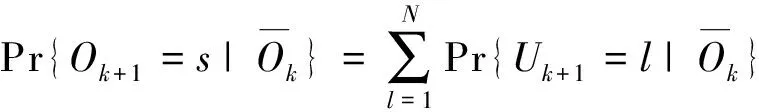
Pr{Ok+1=s|Uk+1=l}=

Pr{Uk+1=l|Uk=i}Pr{Ok+1=s|Uk+1=l}=

根据式(2)，Φ(k)是按照时间递推产生的。Monahan[34]指出Φ={Φ(k),k≥0}是一个Markov过程，因此Φ(k)综合了到时刻k为止的所有信息。令表示一个σ-域， 则代表到时刻k为止的信息集合。如果πk是可测的，那么策略π={πk,k=0,1,…,T-1}称为可行的投资策略，用Ξ表示所有可行策略集合。时刻k，观测到市场状态Ok后，投资者将依据其对不可观测状态Uk分布的判断Φ(k)来预测风险资产的超额收益找到允许策略π∈Ξ，使得投资结束时风险最小。因此，信息部分可观测下的优化问题P(mv)等价地转化为以下信息完全可观测的优化问题

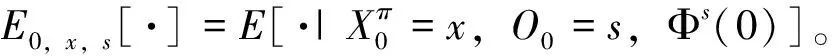
3 模型求解

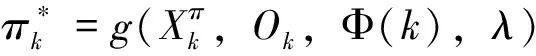
(4)

其中γ=λ-d。由于λ和d都是常数，所以优化问题LP(mv)等价于

因为

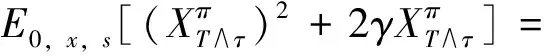
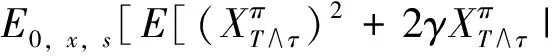
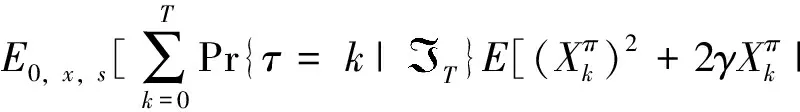
(5)

所以问题LP(mv)等价于

令

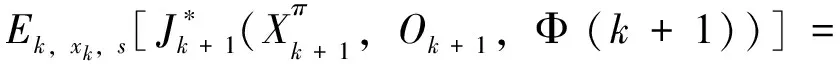
(6)

2γβk(s)xk-γ2Ck(s)

(7)

相应最优策略为

(8)

(9)

(10)

(11)

αT(s)=1

(12)

βT(s)=1

(13)

(14)

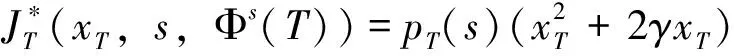
其中

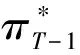
2γβT-1(s)xT-1-γ2CT-1(s)

其中

假定对于k+1，式(7)也是成立的，即

2γβk+1(s)xk+1-γ2Ck+1(s)

根据 Bellman 方程(6)有

其中

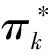
其中

4 最优策略和有效前沿

β0(s)x-(λ-d)2C0(s)-

d2-2d(λ-d)

(15)

(16)

根据C0(s)的表达式，不难发现C0(s)>0，故优化问题(16)的最大值存在。根据一阶最优性条件，使问题(16)达到最优的λ为

(17)

(18)

(19)

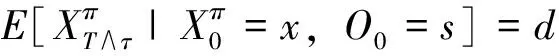
k=0,1,…,T-1

(20)

进一步，可得到相应的有效边界为

(21)

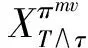
5 特 例

1)当投资者退出市场的时间是确定的，也就是说投资者在时刻T退出市场，即p0(O0)=p1(O1)=…=pT-1(OT-1)=0，pT(OT)=1。此时，问题P(mv)的最优策略和有效边界仍由式(20)-(21)给出，但相应的参数退化为

αT(s)=1;

βT(s)=1;

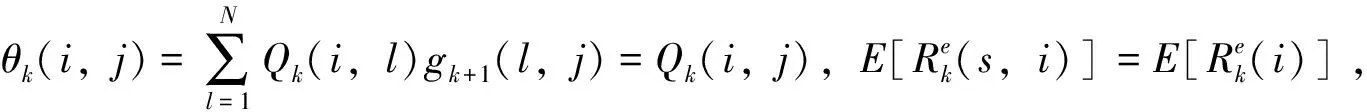
那么，从时刻0初始状态i出发到时刻k状态为j时，信息部分可观测市场中退出时间不确定下投资组合选择问题的最优投资策略为

k=0,1,…,T-1

(22)

相应的有效边界为

(23)

特别的，当投资者退出市场的概率分布与状态无关时，即pk(i)=pk时，式(22)和式(23)同文[14]中只有一个风险资产情况下的结论一致。

6 结 论

本文研究了同时具有可观测状态和不可观测状态的金融市场中，不确定退出时间下的多阶段均值-方差最优投资组合选择问题。我们利用有限状态离散时间隐Markov链刻画不可观测市场状态的演变过程，且状态转移概率是时间的确定性函数。假定风险资产的收益同时依赖于可观测市场状态和不可观测市场状态，无风险资产收益依赖于可观测的市场状态。在投资过程中，随着获得信息的增加，当投资者根据当时观测信息判断发现投资活动不宜继续进行时，会结束投资活动退出市场。因此我们假定投资者退出市场的时间依赖于可观测的市场状态。我们通过应用充分统计量方法，信息部分可观测的投资组合优化问题等价地转化为信息完全可观测的优化问题，再结合动态规划方法和拉格朗日对偶原理，得到了信息部分可观测市场中均值-方差投资组合问题的最优策略和有效边界的解析表达式。我们还发现可观测和不可观测的市场状态以及随机退出时间都对都对最优策略均有显著的影响，且不可观测的市场状态是通过投资者对其概率分布的推断影响最优资产组合策略。

参考文献：

[1]MARKOWITZ H. Portfolio selection [J]. Journal of Finance, 1952, 7: 7-91.

[2]MERTON R C. Lifetime portfolio selection under uncertainty: The continuous-time case [J].The Review of Economics and Statistics, 1969, 51(3): 247-257.

[3]LI D, NG W L. Optimal dynamic portfolio selection: multi-period mean-variance formulation [J]. Mathematical Finance, 2000, 10: 387-406.

[4]ZHOU X Y, LI D. Continuous-time mean-variance portfolio selection: A stochastic LQ framework [J]. Applied Mathematics and Optimization, 2000, 42: 19-33.

[5]LIM A E B, ZHOU X Y. Mean-variance portfolio with random parameters in a complete market [J]. Mathematics of Operational Research, 2002, 27: 101-120.

[6]ZHU S S, LI D, WANG S Y. Risk control over bankruptcy in dynamic portfolio selection: a generalize mean-variance formulation [J]. IEEE Transactions on Automatic Control, 2004, 49:447-457.

[7]LEIPPOLD M, TROJANI F, VANINI P. A geometric approach to multiperiod mean variance optimization of assets and liabilities [J]. Journal of Economic Dynamics and Control, 2004, 8:1079-1113.

[8]BASAK S, CHABAKAURI G. Dynamic mean-variance asset allocation [J]. Review of Financial Studies, 2010, 23: 2970-3016.

[9]BJÖRK T, MURGOCI A, ZHOU X Y. Mean-variance portfolios optimization with state-dependent risk aversion [J]. Mathematical Finance, 2014, 24(1): 1-24.

[10]HAMILTON J D. A new approach to the economic analysis of nonstationary time series and the business cycle [J]. Econometrica, 1989, 57: 357-384.

[11]ZHOU X Y, YIN G. Markowitz’s mean-variance portfolio selection with regime switching: A continuous-time model [J]. SIAM Journal on Control and Optimization, 2003, 42: 1466-1482.

[12]ÇAKMAK U, ÖZEKICI S. Portfolio optimization in a stochastic market [J]. Mathematical Methods of Operations Research, 2006, 63(1): 151-168.

[13]COSTA O L V, ARAUJO M V. A generalized multi-period mean-variance portfolio optimization with Makov switching parameters [J]. Automatica, 2008, 44: 2487-2497.

[14]WU H L, LI Z F. Multi-period mean-variance portfolio selection with Markov regime switching and uncertain time horizon [J]. Journal of Systems Science and Complexity, 2011, 24: 140-155.

[15]HONDA T. Optimal portfolio choice for unobservable and regime-switching mean returns [J].Journal of Economic Dynamics and Control, 2003, 28(1): 45-78.

[17]HAUSSMANN U G, SASS J. Optimizing the terminal wealth under partial information:the drift process as a continuous time Markov chain[J].Finance and Stochastics,2004,8:553-577.

[18]BENSOUSSAN A, KEPPO J, SETHI S P. Optimal consumption and portfolio decisions with partially observed true prices [J]. Mathematical Finance, 2009, 19(2):215-236.

[19]ELLIOTT R J, SIU T K, BADESCU A. On mean-variance portfolio selection under a hidden Markovian regime-switching model [J]. Economic Modelling, 2010, 27: 678-686.

[21]BAE G I, KIM W C, MULVEY J M. Dynamic asset allocation for varied financial markets under regime switching framework [J]. European Journal of Operational Research, 2014, 234: 450-458.

[22]YARRI M E. Uncertain lifetime, life insurance, and the theory of the consumer [J]. The Review of Economic Studies, 1965, 32(2): 137-150.

[23]KARATZAS I, WANG H. Utility maximization with discretionary stopping [J]. SIAM Journal on Control and Optimization, 2001, 39(1): 306-329.

[24]LIU H, LOEWENSTEIN M. Optimal portfolio selection with transaction costs and finite horizons [J]. Reviews of Financial Studies, 2002, 15: 805-835.

[25]郭文旌, 胡奇英. 不确定终止时间的多阶段最优投资组合 [J]. 管理科学学报, 2005, 8(2): 13-19.

[26]BLANCHET-SCALLIET C, EI KAROUI N, JEANBLANC M, et al. Optimal investment decisions when time-horizon is uncertain [J]. Journal of Mathematical Economics, 2008, 44(11): 1100-1113.

[27]YI L, LI Z F, LI D. Multi-period portfolio selection for asset liability management with uncertain investment horizon [J]. Journal of Industrial and Management Optimization, 2008, 4(3): 535-552.

[28]ZHANG L, LI Z F. Multi-period mean-variance portfolio selection with uncertain time horizon when returns are serially correlated [J]. Mathematical Problems in Engineering, 2012, Article ID: 216891.

[29]ZENG Y, WU H L, LAI Y Z. Optimal investment and consumption strategies with state-dependent utility functions and uncertain time horizon [J]. Economic Modelling, 2013, 33: 462-470.

[30]WU H L, ZENG Y, YAO H X. Multi-period mean-variance portfolio selection with state-dependent exit probability [J]. Economic Modelling, 2014, 36: 69-78.

[31]WU H L, LI Z F. Multi-period mean-variance portfolio selection with Markov regime switching and uncertain time-horizon [J]. Journal of Systems Science and Complexity, 2011, 24:140-155.

[32]YAO H X, LAI Y Z, HAO Z F. Uncertain exit time multi-period mean-variance portfolio selection with endogenous liabilities and Markov jumps [J]. Automatica, 2013, 49(11): 3258-3269.

[33]BERTSEKAS D P. Dynamic programming: Deterministic and Stochastic models [M]. Prentice-Hall, 1987.

[34]MONAHAN G E. A survey of partially observable Markov decision processes: theory, models, and algorithms [J]. Management Science, 1982, 28(1): 1-16.