基于主成分分析和遗传算法的模糊神经网络在矿井突水判断中的应用*

2014-03-22王江荣任泰明

计量技术 2014年9期

王江荣　文　晖　任泰明

(兰州石化职业技术学院信息处理与控制工程系，兰州 730060)

0　引言

矿井突水严重危害着煤炭的开采、矿工的生命和财产安全，因此,对矿井突水的预测预报工作显得十分必要，对煤矿安全生产有着重要意义[1-2]。影响煤矿突水的主要因素(指标或特征)有：含水性、水压、隔水层厚度、突水系数、导水性、构造发育、岩性组合、推进步距、工作面斜长等9个因素[3]。这些判别指标之间界限很不明显，存在一定的模糊性、信息的不精确性以及信息叠加性等，特别是信息的叠加会导致突水状况误判的问题。另外，这些判断指标与矿井突水之间存在着很强的非线性关系[4]。为此，该文采用主成分分析(PCA，Principal Components Analysis)法对影响突水状态的指标数据进行信息提炼，把多个彼此相关联的指标变量通过线性组合转化为彼此独立的样本指标，有效地提取原突水状态的指标变异信息，消除指标间信息叠加造成的影响。模糊神经网络具有自学习功能又具有模糊语言表达能力，同时具有高度非线性拟合能力，是集学习、联想、识别、自适应及模糊信息处理于一体的智能信息处理方法。本文拟用模糊神经网络对矿井突水样本数据进行判别(突水，不突水)，较好地解决了信息的不足、环境的模糊性以及判断指标的非线性等问题，并以主成分分析生成的样本数据(或特征向量)作为模糊神经网络的输入，用遗传算法对模型系数及参数进行优化。从淄博矿井突水案例中选取20个典型底板突水资料作为原始的建模样本数据，另选6个原始样本数据作为模型的检测样本数据。实例仿真结果表明本文建立的基于主成分分析和遗传算法的模糊神经网络矿井突水判断模型效果优于常用的神经网络和支持向量机回归等方法，具有一定的借鉴意义。

1　研究方法

1.1　主成分分析

影响矿井突水的因素是多方面的，且各因素的重要性有所不同。在很多情况下，变量之间有一定的相关性，从而使得这些变量所提供的信息在一定程度上有所重叠。主成分分析法[5-6]是一种数据压缩和特征信息提取技术，利用该方法对数据进行处理，可有效地消除高维数据组之间的相关性，使数据降维，数据结构简化，同时保留了所需要的主要信息。

主成分分析法的计算步骤如下：

设X是一个含有n个数据样本和p个变量的二维数据表，X=(xij)n×p。其中列向量(x1j,x2j,…,xnj)Τ对应第j个变量。

1.1.1数据标准化

利用MATLAB提供的函数zscore()或利用式(1)消除数量级和量纲不同造成的影响。

(1)

1.1.2计算样本各维间相关系数矩阵

1.1.3计算特征值与特征向量

利用MATLAB提供的eig()函数求出相关系数矩阵R=(rij)p×p的p个特征值l1,l2,…,lp(l1≥l2≥…≥lp≥0)与相对应的特征向量e1,e2,…,ep，从而有Rei=liei。

1.1.4计算贡献率

1.1.5计算主成分载荷矩阵

设e1,e2,…,em是根据1.1.4节选定的m个主成分特征值对应的特征向量，计算标准化后的各变量x1,x2,…,xp在各主成分上的载荷矩阵，其计算公式：

式中：eij为向量ei的第j个分量。经过计算后，可以得到的主成分载荷矩阵。主成分yi的表达式为：

yi=li1x1+li2x2+…+lipxpi=1,2,…,m

(2)

这样可将p维样本向量(x1,x2,…,xp)转化为新的m维样本向量(y1,y2,…,ym)，达到降维和消除信息重叠(使样本的各个属性之间是相互独立)的目的，并将新的m维向量(y1,y2,…,ym)作为下文模糊神经网络算法的输入向量。

1.2　基于T-S的模糊神经网络

T-S(Takagi-Sugeno：T-S)神经网络具有较强的自学习和联想功能，人工干预少，精度较高，对专家知识的利用也较好。但缺点是它不能处理和描述模糊信息，不能很好利用已有的经验知识，对样本的要求较高；模糊系统相对于神经网络而言，具有推理过程容易理解、专家知识利用较好、对样本的要求较低等优点，但它同时又存在人工干预多、推理速度慢、精度较低等缺点，很难实现自适应学习的功能。将二者有机地结合起来，可起到优势互补，取长补短[8-9]。

1.2.1T-S模糊神经网络计算步骤[10-12]

1)对于k维输入向量y=[y1,y2,…,yk]，根据模糊规则计算各输入变量yj的隶属度，隶属度函数采用高斯型：

(3)

2)将各隶属度进行模糊计算，模糊算子采用连乘算子：

(4)

3)T-S模糊神经网络输出数学表达式为：

(5)

4)计算误差

(6)

式中，yd是网络期望输出；yc是网络实际输出。

5)修正系数和参数

T-S模糊神经网络根据网络输出和期望输出的误差平方和e来修正系数和参数。

系数修正表达式：

(7)

式中，m为对应层的结点个数；a 为网络学习率；yj为网络输入参数；ωi为输入参数隶属度连乘积。

参数修正：

(8)

1.2.2基于T-S模糊神经网络的矿井突水样本识别模型

采用T-S模糊神经网络对矿井突水样本分类，分为T-S模糊神经网络构建、训练和预测3个部分。模糊神经网络的构建确定了网络的输入和输出数量、隶属度函数和参数的个数；模糊神经网络训练采用选定的样本数据，测试数据选用其它样本数据。

1.2.3实验数据

影响矿井突水的因素有：含水性x1、水压x2、隔水层厚度x3、突水系数x4、导水性x5、构造发育x6、岩性组合x7、推进步距x8、工作面斜长x9等9个因素。选取淄博矿井突水案例中20个典型底板突水资料作为原始标准样本数据[3]，以这20个样本数据作为建模数据，具体数据见表1。表1中的实际突水性一列里的数值“1”表示不突水，数值“2”表示突水。

表1　淄博煤矿突水各影响因素与实际突水量(训练样本)

注:突水量单位：m3/h；含水性、突水系数、导水性、构造发育、岩性组合均为量化值，无量纲。

1.2.4数据的PCA处理

首先对表1中的样本数据进行标准化处理，然后对标准化处理后的样本数据进行PCA处理。其中，相关系数矩阵的特征值及贡献率见表2。

通过表2中的数据可知，取前4个特征值累计贡献率达84.5308%，根据累计贡献率大于80%也可以接受的原则，提取前4个特征值(其中3个大于1)为主成分。根据PCA主成分表达式的系数矩阵(主成分的载荷矩阵)得到新因子Y1，Y2，Y3和Y4与原始变量(标准化后)之间的关系表达式为：

Y1=0x1+0.6315x2+0.5301x3+0.2313x4+

0.0154x5-0.0438x6+0x7+0.4824x8+

0.1784x9

(9)

Y2=0x1+0.0249x2+0.3662x3-0.4707x4-

0.3761x5+0.3625x6+0x7-0.3490x8+

0.4991x9

(10)

Y3=0x1+0.0470x2-0.1587x3+0.4244x4+

0.4746x5+0.6874x6-0x7-0.1440x8+

0.2721x9

(11)

Y4=0x1-0.0632x2+0.2235x3-0.4933x4+

0.7914x5-0.2423x6+0x7-0.0221x8+

0.1309x9

(12)

将4个主成因子Y1，Y2,Y3和Y4作为模糊神经网络的4个输入指标。结合表1，由4个主成分生成新的矿井突水指标，新指标见表3。

表2各项指标相关系数矩阵的特征值及贡献率

主成分序号特征值差值贡献率%累计贡献率%12　30660　645032　951432　951421　66160　645023　736756　688131　14620　343416　374473　062540　80280　120811　468384　530850　68200　29849　742994　273660　38360　36635　479799　753470　01730　01730　2466100　000082　6653e-0332　6653e-0333　8076e-032100　0000900100　0000

表3　4个主成分生成的矿井突水状态的新判别指标

1.3　基于遗传算法的参数修正方法

本文利用遗传算法工具箱的GUI进行参数优化计算[13]。适应度函数为：

(13)

打开遗传算法的GUI，在Fitnessfunction窗口输入@fitess(函数的计算过程由MATLAB编写，在此略去)，在Number of variables窗口输入变量数目104，边界约束：Lower输入0.01*ones(1,104)；Upper输入3.5*ones(1,104)，种群规模选50，迭代次为1000，其它参数选默认值。

训练结束后，输出训练样本是否突水判断的拟合值，并近似处理，结果见表3(正确：表3第7列)。和实际突水状态值比较，本文方法的预报值精确率为100%。可见经训练样本创建的突水判断模型具有很高的精确性和稳定性。下面我们对本文所创建的模型作进一步测试，测试样本见表4。

表4　测试样本[3]

将表4待判样本数据标准化后代入文中1.2.4节由PCA提取的4个主成分表达式(9)～(12)得到待测样本的主成分指标见表5。

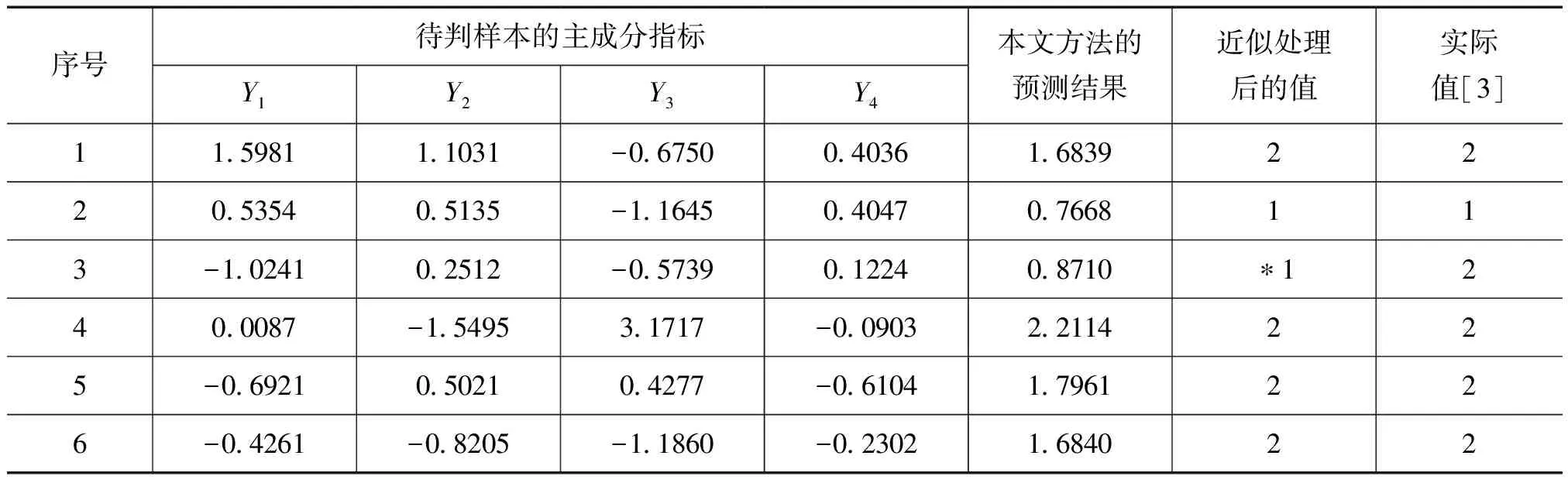
表5　待判样本的判别结果及有关数据

在MATLAB命令窗口输出104个优化参数(此处省略)，将适应度函数中训练集自变量输入矩阵换成测试集自变量输入矩阵(数据见表5中主成分所在列)，代入优化参数(训练样本所得)求出6个测试样本突水性的预报值，具体结果见表5。表5数据显示本文方法的预测正确率为83.33%(错了一个)。作为比较下面给出另三种方法的预测结果(训练样本和测试样本不变)，具体数据见表6。

通过对比表5和表6的预报值，本文方法的预报结果显然优于表6中的方法。究其原因，本文方法充分利用PCA法能消除变量之间相互信息叠加而产生的影响，用少量指标表征突水特性；利用模糊神经网很好地解决了突水环境的模糊性和非线性性。同时发挥了遗传算法所具有的全局搜索能力，优化了模型的系数和参数，增强了模型的精确性和稳定性。而表6中的方法有着明显的缺陷，所以误差较大。

2　结束语

结合矿井突水的信息特征，本文提出了基于PCA和模糊神经网络的突水判别预测方法。在突水判别预测过程中，利用PCA法处理原始数据后，不仅可以用少量的指标变量有效地表征矿井突水特性，而且能消除由于变量之间相互信息叠加而产生的影响。研究结果表明，对数据信息进行PCA法处理后，矿井突水类型(突水或不突水)的判别精度比单纯使用模糊神经网络判别法有较大提高，也比其它一些方法效果要好。

T-S模糊神经网络的权系数和高斯隶属度函数参数较多，采用遗传算法优化后，提高了T-S模糊神经网络模型计算结果的稳定性，摒弃了模型对权值选取的主观性和敏感性，充分发挥了模糊系统和神经网络的各自优势，使模型的泛化能力得到了加强，而且多次运行识别结果保持一致。优化后的T-S模糊神经网络模型的准确性和稳定性远好于单一的神经网络和支持向量机回归等模型，值得矿业技术人员借鉴。

[1]张立新,李长洪,赵宇.矿井突水预测研究现状及发展趋势[J].中国矿业,2009,18(1):88-90

[2]张自政,杨勇,等.模糊评价分类模型在矿井底板突水判别中的应用[J].矿业安全与环保,2010,37(6):41-43

[3]张文泉.矿井底板突水灾害的动态机理及综合判测和预报软件开发研究[D].青岛:山东科技大学,2004:164-166

[4]邱秀梅,王连国.煤层底板突水人工神经网络预测[J].山东农业大学学报,2002,33(1):62-65

[5]杜红兵，王雪莉.基于主成分分析法的空管多指标安全综合评估研究[J].中国安全科学学报，2009，19(7):124-128

[6]张文，陈剑平，秦胜武，等.基于主成分分析的FCM法在泥石流分类中的应用[J].吉林大学学报，2010，40(2):368-372

[7]王英，黄容，段继红.基于主成分分析的重庆市房地产供求协调关系的研究[J].工程管理学报,2012,26(5):089-093

[8]谭涛,任开春,等.模糊神经网络技术[J].重庆文理学院学报(自然科学版),2011,30(1):71-74

[9]钱光耀,夏二勇,王沪阳,等.基于遗传算法和小波神经网络的传感器输出拟合方法研究[J].计量技术，2011(9)：3-6

[10]王小川,史峰,等.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:288-289

[11]周润景,张丽娜.基于MATLAB与fuzzyTECH的模糊与神经网络设计[M].北京：电子工业出版社，2010：196-201

[12]周燕，王里奥.模糊神经网络在重庆市饮用水原水水质评价中的应用[J].三峡环境与生态，2010，3(1):33-35