挤出机机筒内径测量仪的数据后处理技术
2014-03-22谢惠琴杨铁牛苏景贤侯曙光
谢惠琴 杨铁牛 苏景贤 侯曙光
(1.新美亚科技(深圳)有限公司,深圳 518045;2.广东五邑大学 机电工程学院,江门 529020;3.广东永坚精机(江门)有限公司,江门 529000)
0 引言
测量误差的大小是衡量测量仪器的重要指标,而测量仪的数据后处理是提高仪器测量准确度、降低测量偏差的一个重要方法。本文对用内径测量仪测量挤出机机筒内径的测量数据进行分析后,给出了对数据后处理的方法,从而达到提高测量精度的目的。根据江门某企业所提出的要求,针对双螺杆挤出机机筒的内径测量设计了一款测量头。其测量系统由测量头、NI USB6210数据采集卡、24V直流稳压电源、电涡流传感器及其相应的处理器、激光传感器、电路板、若干电缆线和导线等组成。
通过实验验证测量头所采集的数据存在较大的误差。因此,对所开发的测量仪进行数据后处理的研究有着必要性和现实性。
1 测量数据采样与误差分析
如图1所示为∞型双螺杆挤出机机筒磨损前后的示意图。针对其内径测量设计了一款测量头,如图2所示。

图1 被测机筒形状

图2 测量头三维造型图
经分析知:测量误差主要来源于传感器的原理误差和被测对象尺寸范围及其材料的标定误差[1-2]。
由传感器原理知,其所测得的位移量是指:以探头中心所对应被测机筒截面为圆心,1.5倍[3]探头直径的圆区域内,传感器对被测表面所测值的平均值。经实验表明:据此原理[4]所研制的挤出机机筒内径测量仪所测得的直径量与真实值存在较大的偏差,实验情况如图3与表1所示。

图3 针对φ68机筒孔径实验所测直径曲线图

表1 理论直径与实测直径对比 (单位:mm)
从图3知:当测量仪对机筒严重磨损截面进行测量时,其结果比实际值偏小,即测量结果发生“钝化”;当测量仪对两严重磨损截面之间进行测量时,其结果比实际值偏大,即测量结果发生“腐化”。而因保护电压极限,当测量仪对机筒开槽处或排气口进行测量时,被测位移量将大于传感器线性量程的最大测量值,该区域内的值保持线性量程的最大值不变。
当被测机筒直径尺寸为标定直径尺寸时,测量仪所测得的数据误差较小;当被测机筒直径尺寸非标定直径尺寸时,测量仪所测得的数据误差较大。
2 测量数据后处理的原理
本文研究的测量仪,其测量方式为动态测量。测量过程中,测量仪器任一时刻所测得的值减去被测量该时刻的理论值,所得代数差为动态测量误差e(t)。
e(t)=x(t)-x0(t)
(1)
式中,x(t)为被测量的测量值;x0(t)为被测量的真值;t为一个过程参变量。
对动态测量误差大小的评定可采用先验分析法或数据处理法[5]。从文献[6]得到启发,本文首先将测量仪对机筒所测得的数据与其真值进行比较,结合传感器测量原理分析出误差的系统特性。然后,结合其测量数据构建误差补偿函数,进行测量结果的修正。
对动态测量误差的处理一般包括数据预处理、误差分离和误差修正三方面内容[7]。
预处理:首先去除测量仪所测得的起始段和末尾段的无效数据,截取中间段的有效数据;其次剔除中间段中的缺口、开槽及排气孔的异常数据。
误差分离:对预处理后获得的数据进行测量误差分析与分离,得出误差来源,找出符合一定条件的极值,并确定其位置。
误差修正:根据所构建的数据补偿函数得到对应修正值,然后将其补偿到对应测量值中,实现测量值的修正。
3 测量数据后处理函数的构建
通过实验数据分析,得到误差分布规律为:当测量值为峰值时,测量结果比真实值偏小,即测量误差为负;当测量值为谷值时,测量结果比真实值偏大,即测量误差为正;测得数据分布曲线与机筒磨损情况一致,呈波浪形分布;以测量峰值或谷值所在位置为圆心,1.5倍探头直径圆区域面积内的数据关于峰值或谷值所在位置对称分布。
根据电涡流形成原理:当在被测表面上形成的涡流距离涡流中心点越近,其所形成的电涡流强度越强。因此,越靠近极值所在位置处,测量点邻域对极值的影响程度越大,反之影响程度越小。故本文选用以极值所在截面位置为中心,探头半径区域内所测得的直径为构建误差补偿函数的数据依据。
假设所测得直径中,直径dn为所测得直径的极值,直径dn-i与dn+i为以极值所在截面位置为中心,探头半径为半径的区域内所测得的直径,则极值与各直径之差为:
Δi0=dn-dn-i,Δi1=dn-dn+i
(2)
式中,Δij为极值与其所在直径截面为中心,探头半径为半径的区域内所测得的直径对应各直径之差,mm(其中i、j∈n,j=0,1)。
当dn-i与dn+i的对应截面位置分别关于极值所在截面位置对称时,则有
(3)
式中,Δi是指极值与各对称截面直径差值的平均值,mm(i∈n)。
若所选定区域内无对称截面的直径量时,则无需进行式(3)运算。(所选直径其截面位置需在极值截面位置为中心、探头半径为半径的区域内,其直径个数不定。)
根据上文所提线性补偿思想,并通过大量数据的实验,得到了本文的数据补偿(误差修正值)的函数为
ei=∑KiΔi
(4)
式中,ei为对应极值的误差修正值,mm;Ki为影响系数;(其中i∈n,且Ki≤1)。
从式(4)可知,影响系数大小决定了修正值的大小,同时该系数的确定决定了补偿函数的可靠程度,故需从其相关因素和特性进行确定。
从上文知,离极值所处位置越近的直径,对极值影响程度越大, 则K值越大;机筒直径越大,被测面的曲率越小,测量误差也越小,则修正值也越小,此时K值可取偏小。
综上所述,并通过实验验证表明,Ki的取值为
(5)
式中,d为电涡流传感器探头直径,mm;D为被测机筒受损前的理论直径,mm;δi为影响系数因子(i∈n,δ1>δ2>δ3…>δi,且δi≤1)。
通过实验,得到了较理想的δi值。本测试实验中,取i=1,2,3。当机筒直径非标定直径时,取δ1=0.65,δ2=0.25,δ3=0.1;当机筒直径为标定直径时,取δ1=0.45,δ2=0.25,δ3=0.2。
当机筒无磨损时,同样可以使用该测量仪对机筒内径进行测量,用于实现检验机筒的合格性。但此时,测量仪所测得数据对整机而言,具有相同的测量误差,且误差均为负值。据此,并结合电涡流传感器原理,通过实验不断验证与优化,得到了对机筒的测量误差补偿函数
(6)
式中,e为无磨损机筒的测量误差补偿值,mm。
得到了补偿函数后,根据式(7)对测量值进行误差补偿,得到最终的测量结果,提高了测量仪的测量可靠性。
[Di]=Di+ei(或e)
(7)
式中,[Di]为补偿后的直径测量值,mm;Di为补偿前的直径测量值,mm(i∈n)。
由上可知,本文所构建的修正函数,是以实时所得数据为依据,在线修正补偿函数的权值大小,可以适应不同零件的测量,灵活性较强。
4 测量数据后处理的程序设计
4.1 测量数据后处理程序设计思想
针对各种测量情况——不同长度、不同直径、不同材料、不同误差情况和不同测量数据,均需有相应数据修正,才能充分提高测量仪的测量可靠度,降低测量误差。
根据上文,确定了如图4所示的数据后处理流程图。图中,Vi为电涡流传感器所测得的电压值,V;Si为Vi转化为其对应的被测位移量,mm;Xi为被测机筒截面位置,mm;变量l、m、n、i、r、t∈n。
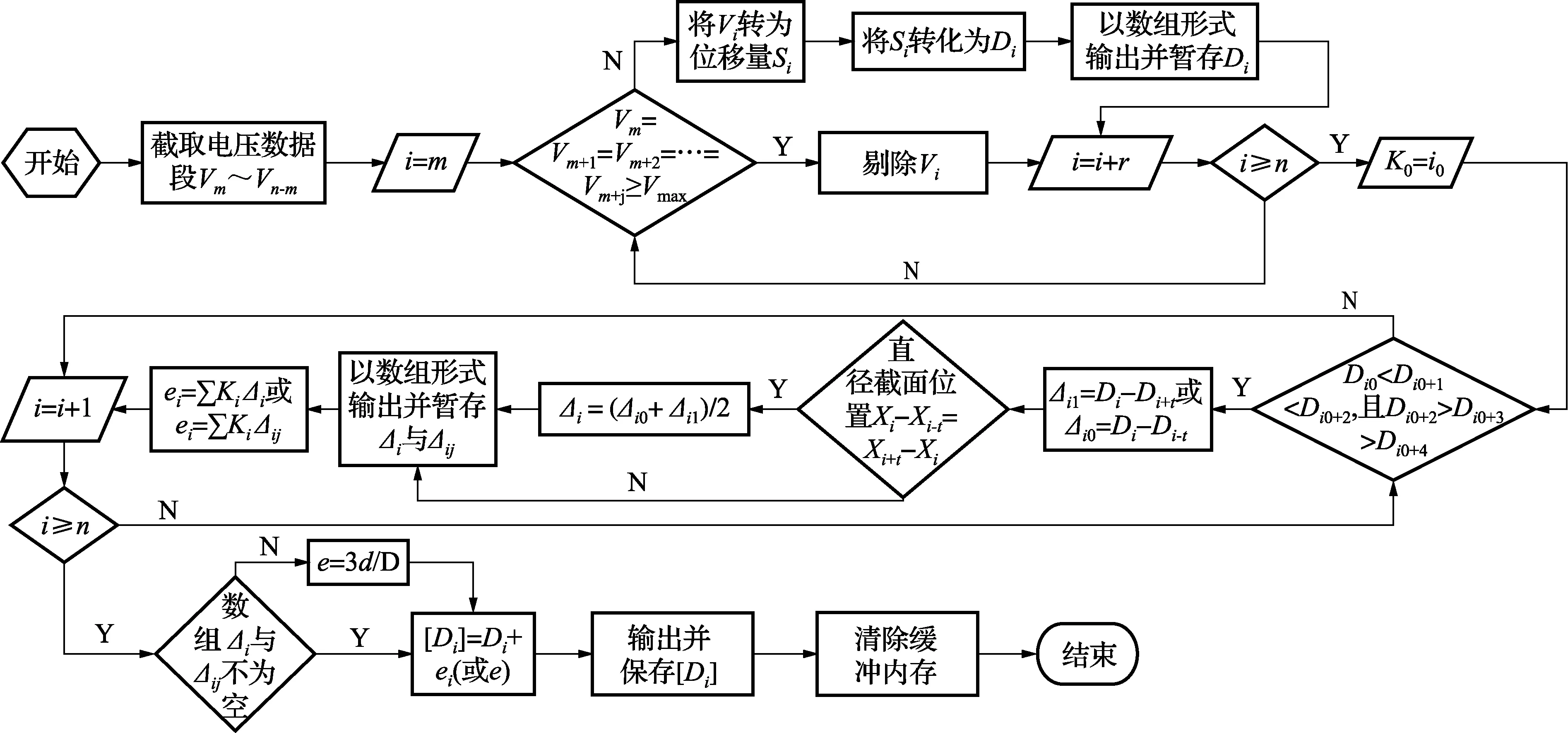
图4 测量数据后处理程序设计流程图
4.2 测量数据后处理程序的编写
为了实现4.1中的程序设计思想和要求,本文采用LabVIEW软件和C语言,利用条件循环顺序结构完成了程序编写。运用LabVIEW软件中的函数有:采用条件和for循环结构函数实现了测量数据的截取、剔除与分离;采用比较和布尔函数判断了符合一定条件的极值;使用数值函数完成了修正函数的建立;采用数组函数与波形显示控件实现了测量结果的实时显示;使用移位寄存器函数实现了数据的暂存功能;采用局部变量、文件路径、文件I/O、字符串、数组等函数实现了数据的保存;采用顺序结构实现了各功能模块之间的衔接。最后,在数据处理完毕后,采用C语言实现了暂缓内存冗余数据的清除,为重复测量准备条件。
5 测量数据处理前后的对比
根据文中的数据后处理方法与原理,结合本文构建的补偿函数,本文对实验数据进行修正,其前后对比如表2所示。

表2 数据处理前后比较 单位:mm
由表2可知,最大值处即磨损最严重处的直径量修正了0.50458mm,即偏差由0.77345mm降低为0.26887mm。
6 结论
数据后处理技术是提高测量仪测量准确度的必然措施,用于保证测量仪的实用性。通过本文所构建的数据补偿函数与数据后处理技术,并结合相关实验验证表明,本系统实现了数据后处理的功能要求,对所测得的数据进行了相关的误差补偿,提高了测量仪的测量准确度,降低了测量偏差,给企业带来了一定的经济效益。
[1]叶子郁,朱目成.应用脉冲涡流检测金属表面裂纹的研究[J].计量技术,2005(10):16-18
[2]杨宾峰,罗飞路.脉冲涡流无损检测技术对不同截面形状裂纹的定量检测研究[J].计量技术,2006(6):5-7
[3]上海冉普电子科技有限公司.RP6600/6600XL系列电涡流传感器,http://www.ranpucn.com/zl-cgq-01.asp
[4]谢惠琴,杨铁牛,侯曙光.注塑机机筒内径磨损量的检测方法研究[J].制造业自动化,2011,33(12):17-19
[5]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2002
[6]戴祯建.能源计量数据处理方法——适时修正法[J].计量技术,2003(4):47-49
[7]费业泰,卢荣胜.动态测量误差修正原理与技术[M].北京:中国计量出版社,2001
