基于随机前沿生产函数的我国工业用水效率影响因素研究

卞锦宇,刘 恒,耿雷华,姜蓓蕾,方 瑞

(1.南京水利科学研究院,江苏 南京 210029； 2.水文水资源与水利工程科学国家重点实验室,江苏 南京 210029; 3.江苏省水文水资源勘测局,江苏 南京 210029)

长期以来,水资源利用方式粗放、利用效率不高、水资源供需矛盾突出是制约我国可持续发展的主要瓶颈之一。目前,全国新增取用水量集中在城市、工业,所以水资源保障和经济发展的关系突出体现在城市、工业对水资源的需求和水环境的变化对工业经济的影响。2011年中央明确提出了确立用水效率控制红线,包括提出了以万元工业增加值用水量为考核指标的用水效率红线,坚决遏制工业用水浪费。随着水资源供需矛盾的凸显,如何将有限的水资源实现高效利用,促进工业生产的高效发展,是实施最严格水资源管理的一项重要内容。

用随机前沿法度量技术效率已经在许多领域得到应用,但在水资源管理方面应用还较少,我国近年才开始出现相关研究,同样在工业用水效率方面的应用很少。Karagiannis等[1]用随机前沿技术分析灌溉用水的技术效率;孙爱军[2]提出用随机前沿生产函数对工业水资源利用效率进行分析,陈关聚等[3]运用随机前沿技术测度了我国2003—2010年31个省份工业全要素水资源使用效率及影响因素。总体上,现有的研究主要集中于工业用水技术效率的评估与测算,对影响因素的分析还不深入,而从用水效率红线出发,结合工业用水效率红线考核指标进行分析的研究比较少见。

本文以全国31个省(市、区)万元工业增加值用水量为研究对象,围绕可能影响用水效率的诸多因素,建立我国基于随机前沿生产函数的工业用水效率分析模型,辨识影响工业用水效率的核心因子,为我国未来工业用水效率预测及用水效率红线调控提供科学依据。

1 指标选择与数据来源

现有文献中建立的随机前沿生产函数多数将资金、劳动力、用水量等作为投入变量,笔者在这些变量的基础上,进一步分析自然资源、社会经济、科学技术、生态环境和管理制度等对工业用水效率的影响因素,具体表述各因素，如水资源条件、城市化进程、高用水行业分布、科学技术投入、生态治理及水价杠杆等,选择表征这些因素的定量化指标来反映其对工业用水效率的制约或促进作用。最终确定反映工业用水效率影响因素的指标变量，见表1中的x1～x10。

x1表征了水资源条件对用水效率的影响,从经济学意义上讲,资源的稀缺性决定了资源的价值及其利用方式。一个地区的水资源丰缺程度可以影响人们对水资源的态度,进而影响用水和管水行为。根据相关的统计数据,若排除其他因素,总体上水资源丰沛区用水效率要低于缺水区。

x2,x3,…,x6为反映人口、经济对工业用水效率的影响因素。随着城市化进程、经济的发展,工业产业结构不断优化,用水效率逐步提高。

x7,x8为反映科技对工业用水效率的影响因素。科技投入比例越高,高新技术产业越发达,工业用水效率越高。

x9,x10为反映管理对工业用水效率的影响因素。考虑指标的可量化性,采用废水达标排放率及水价反映水资源管理的政策、法规和制度对工业用水效率的综合影响。

本文研究范围覆盖全国31个省(市、自治区),以省级行政区为研究单元,收集1997年—2010年全国31个省区工业用水效率及相关影响因素指标数据,数据主要来源于同时期的各省、自治区、直辖市统计年鉴，以及《中国水资源公报》《中国统计年鉴》《中国水利统计年鉴》《中国环境统计年鉴》《城市供水统计年鉴》《中国高新技术产业年鉴》《中国科技统计年鉴》《中国人口统计年鉴》和中国气象局资料等。

表1 工业用水效率指标变量

2 模型分区

工业用水效率受气候、地理等自然条件影响较小,而工业产业结构、经济技术条件等对其的影响较大,因此从资源条件、产业结构、经济技术投入等方面考虑人均水资源量、高耗水行业产值占工业总产值比重、工业产值占GDP比重、人均工业产值、高新技术产业产值占工业产值比重、大中型工业企业R&D经费支出占主营业务收入比重、科学技术支出占财政支出比重等指标作为工业用水效率分区指标,反映不同程度的资源压力、经济技术投入及不同的高耗水产业分布对我国工业用水效率的影响,根据地区工业用水效率的提升潜力特征进行分区。

采用主成分分析法将全国31个省(市、自治区)进行分区,主成分分析的基本思想是将原来众多具有一定相关性的变量重新组合成新的少数几个互相无关的综合变量来代替原来变量,这些新的综合变量称之为主成分。

根据主成分累计贡献率超过85%的原则,提取了分析年份的主成分因子,并计算指标x1～x7在各主成分因子荷载值。以2010年为例(表2),第一主成分描述了工业发展规模(x3)、技术进步(x5，x6，x7)以及工业结构(x4),具有较强的综合性；第二主成分因子主要受水资源条件(x1)和产业结构(x2)的影响；第三主成分是受工业结构(x4)为主；第四主成分主要受资源环境(x1)因素影响； 第五主成分受工业结构(x4)和技术进步(x6)因素影响。

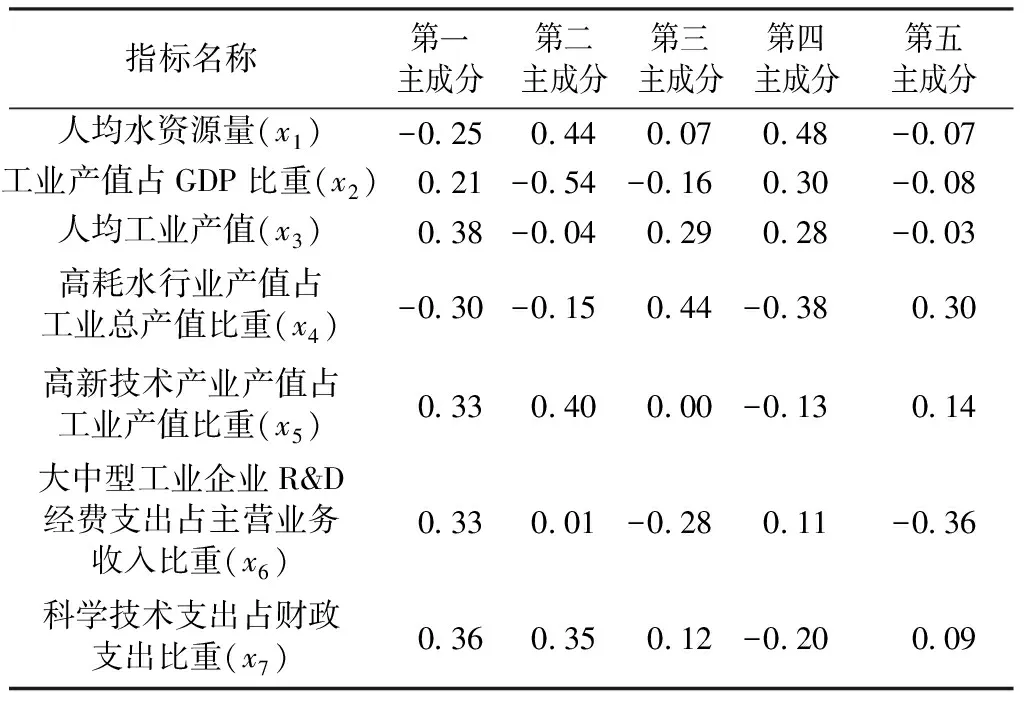
表2 2010年工业用水效率主成分因子荷载值

以2010年全国31个省区的x1～x7的指标数值,计算各主成分综合得分,需要说明的是:各主成分综合得分的高低和正负取值,并不代表用水效率及驱动因素的绝对大小,而是说明各地区的相对位置。综合得分越大,说明各主成分的驱动/约束力越大,根据全国及31个省区的各主成分综合得分,采用聚类分析法进行分类,在此基础上,根据地理位置及综合得分结果,将全国划分为4类地区,见表3。

表3 工业用水效率分析模型分区

3 模型构建方法

3.1 随机前沿生产函数简介

随机前沿生产函数(SFAP)从生产函数角度测量技术效率[4]。SFA是一种随机参数模型,主要用来测量决策单元的生产前沿和成本前沿[5]。SFA的突出特点是在过去应用回归建立决策单元前沿面的基础上做出进一步的改造,将传统的模型误差项分成了两部分:随机误差(v)和管理误差(u)。前者包括了观察误差、不可预期的消耗、可供水量的变化和国际市场构成的改变等不可控因素;后者包括了决策单元的管理、水资源配置、利用和计划制定等方面的内容。

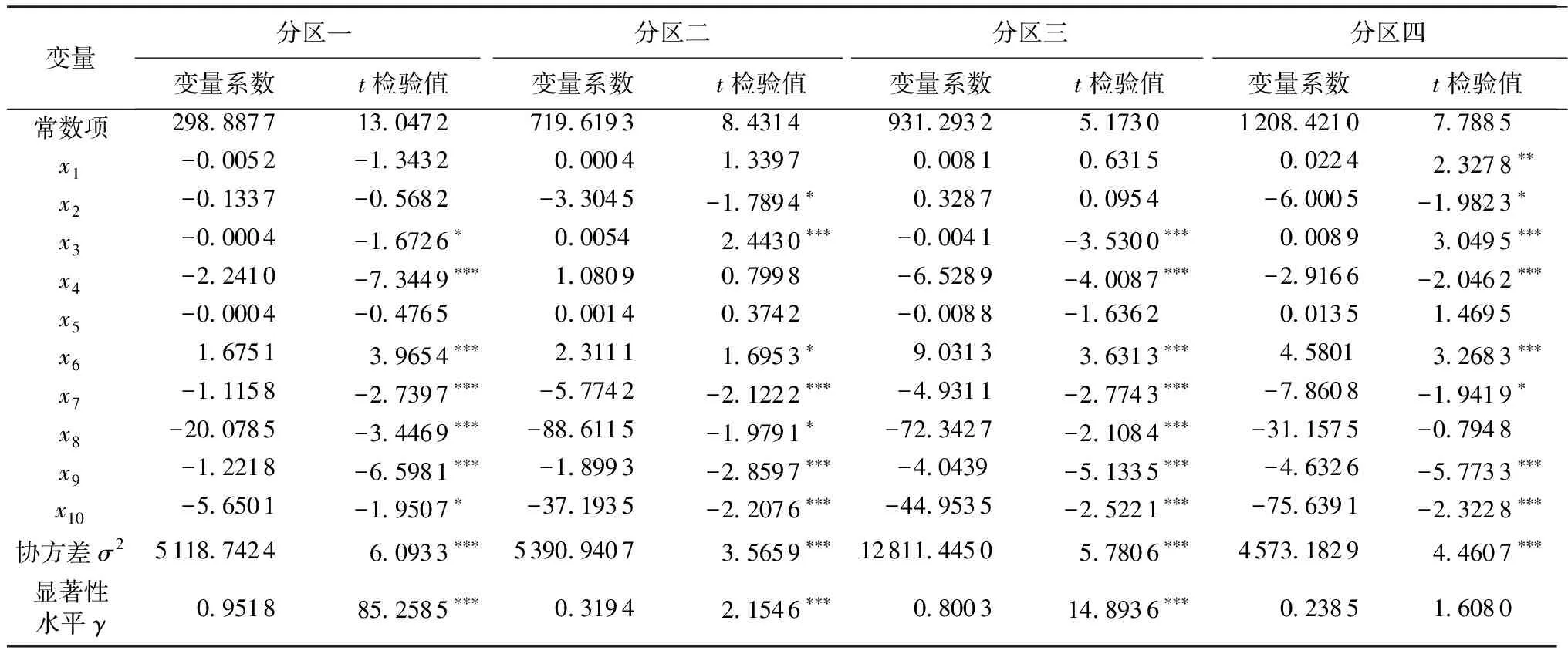
表4 变量系数拟合结果

注:*,**,***分别表示通过了显著性水平为10%,5%,1%的检验。

模型形式为

(1)

式中：yt为产出;xjt为投入的各种要素；βj为变量的系数；vt为随机误差；ut为管理误差；j=1，2，…，n。

在投入变量数目不多的情况下,可以采用超越对数函数构建随机前沿生产模型,但当投入变量较多时,或是变量间存在较大的多重共线性,一般采用常规的C-D函数形式:

(2)

3.2 修正的随机前沿生产函数

目前随机前沿生产函数在工业用水技术效率测算的应用方面,生产指标多为工业产值,投入变量一般为资金、劳动力、用水量等[2-3,6]。在农业用水效率测算方面,有一些研究将单位面积产值或产量作为生产指标[7-8]。

借鉴农业用水效率测算分析中产值指标单位量化的方法,对产出、投入指标做必要的修正,在工业用水效率随机前沿模型中,生产指标用人均产值替代一般的总产值,各投入变量也采用单位量化值或相对值,如用水量采用万元工业增加值用水量,固定资产净值采用人均值,工业从业人员采用占总人口比例等,这个调整的主要目的是为了将研究中工业用水效率指标即万元工业增加值用水量能直接体现在模型中,便于指标的拟合及预测。

采用frontier4.1软件对式(2)进行拟合计算后得到β0～β10参数值,对式(2)进行变换后可得到工业用水效率万元工业增加值用水量:

(3)

再将式(3)适当整理,可形成调整后的工业用水效率随机前沿生产模型:

(4)

式中：yt为万元工业增加值用水量；x1～x10为各影响因子,具体见表1。

4 模型拟合结果

采用frontirer4.1软件对各分区建立的工业用水效率随机前沿生产模型进行计算,得到各变量拟合参数及相关参数,拟合结果见表4。

根据4个分区工业用水效率随机前沿生产模型变量拟合结果,变量x1～x5对工业用水效率的正负影响不确定,在四个分区中有的呈正效应,有的呈负效应,如人均工业产值、工业从业人员比重、人均固定资产净值3个变量在分区一、三中呈正效应,在分区二中呈负效应,在分区四中呈不同效应。这3个变量主要反映工业经济发展状况,在工业经济状况相对较好的分区一和分区三中反映了工业经济发展较好对区域用水效率的正面影响,在工业经济发展较弱的分区二、四中这种作用则无法体现。分区一是人均水资源量较少的地区,相对而言人均水资源量成为约束指标,形成提高区域用水效率的压力,因此在该区成为影响用水效率的负效应。变量x6～x10对工业用水效率的正负效应在4个分区中是统一的,除高耗水行业产值占工业总产值比重对工业用水效率呈负效应外,其他四个变量都呈正效应,并且这5个变量对用水效率的影响显著性也要明显大于前5个变量。

4个分区1997—2010年模型拟合误差分析结果(如表5所示),误差最小的为分区四,最大的为分区三,误差都不大于17%,相关系数也均在0.7以上。较低的误差说明本次建立的全国4个分区工业用水效率分析模型是合理可行的,可用于未来工业用水效率的定量预测及相关影响因素分析。

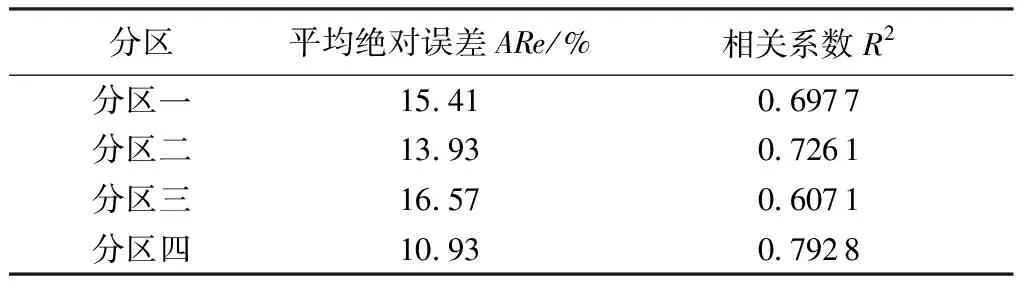
表5 工业用水效率随机前沿生产模型误差分析

5 变量排序

在确定各变量系数的基础上,计算各变量对应变量万元工业增加值用水量的影响系数,以此进行变量排序。影响系数按式(5)计算:

Ei=(ximax-ximin)Ci

(5)

式中：Ei为第i个变量的影响系数；ximax,ximin分别为第i个变量数值的最大值和最小值；Ci为第i个变量的系数值。

表6为4个分区各变量的影响系数及排序结果,4个分区各变量排序略有差异,分区一排序第一的是x6,分区二和分区四排序第一的是x9,分区三排序第一的是x3。统计各变量排序位次及出现频率,4个分区中排序前5 的变量主要有x3,x9,x6,x10,x8,说明这几个变量是影响万元工业增加值用水量的核心影响因子。

表6 各分区变量影响系数及排序结果

6 结 论

a. 采用修正的随机前沿生产函数法进行多元变量与应变量的拟合,以万元工业增加值为应变量、10个影响因子为自变量,建立了全国31省(市、区)4个分区的工业用水效率分析模型,通过模型拟合误差分析,4个区的模型平均绝对误差都小于17%,说明所建模型精度较高,可为未来我国工业用水效率预测及用水效率红线调控提供参考。

b. 根据拟合出的各变量系数的正负可以判断,变量x6～x10对工业用水效率的正负效应在四个分区中是统一的,除高耗水行业产值占工业总产值比重对工业用水效率呈负效应外,其他4个变量都呈正效应,说明建立的模型符合工业用水效率影响因素的作用机理。

c. 通过变量排序4个分区中排序前5 的变量主要有x3,x9,x6,x10,x8,说明这几个变量是影响万元工业增加值用水量的核心影响因子。

d. 常规的随机前沿生产函数应用于工业用水效率,其投入变量多为劳动力、资产、水资源量等绝对指标,本次对其进行修正,采用相对指标作为投入产出变量,不仅扩展了投入变量的范围,同时将万元工业增加值用水量直接引入至模型中,便于用水效率红线调控与考核,是随机前沿生产函数在水资源领域应用的拓展尝试。

参考文献：

[1] KARAGIANNIS G,TZOUVELEKAS V,XEPAPADEAS A.Measuring irrigation water efficiency with a stochastic production frontier[J].Environmental and Resource Economics,2003,26:57-72.

[2] 孙爱军.基于随机前沿函数的工业用水技术效率研究[D].南京:河海大学,2007.

[3] 陈关聚,白永秀.基于随机前沿的区域工业全要素水资源效率研究[J].资源科学,2013,35(8):1593-1600.

[4] COELLI T J, PRASADA RAO D S, BATTASE G E.An introduction to efficiency and productivity analysis[M].Boston:Kluwer Academic Publishers,1998.

[5] KUMBHAKAR S C, LOVELL C A K.Stochastic frontier analysis[M].New York:Cambridge University Press,2000.

[6] 戴卓,代红梅.中国工业行业的技术创新效率研究.经济经纬[J].20124:90-94.

[7] 刘军.农业用水效率模型研究[J].农村经济与科技,2013,24(1):25-26.

[8] 王学渊,赵连阁.中国农业用水效率及影响因素[J].农业经济问题,2008(3):10-18.