抛物线形断面渠道收缩水深简化计算通式

滕 凯

(齐齐哈尔市水务局,黑龙江 齐齐哈尔 161006)

收缩水深是关系过水建筑物下游水跃类型及消能工形式的重要水力参数,因此,研究收缩水深的简化计算对提高设计工作效率具有重要意义。抛物线形断面具有受力性能好、水流条件优越、便于机械化施工等优点,被越来越广泛地应用于灌溉及排水渠系工程中[1-2]。有关抛物线形断面收缩水深简化计算方面的研究成果已有较多,文辉等[3]给出了半立方抛物线断面收缩水深的简化计算公式,赵延风等[4-9]分别给出了二次抛物线形及三次抛物线形断面收缩水深的简化计算公式。为了解决目前简化计算公式存在的不具通用性、不便实际工作的问题,赵延风等[10]采用基线函数增量法给出了该类断面收缩水深的简化计算通式,具有一定的实际意义,但因该通式求解需要分别计算3个中间变量方可获得最终结果,求解过程过于烦琐,实际应用仍不方便。本文通过对该类断面渠道收缩水深计算公式的变形整理,引入已知综合参数及无量纲水深参数,在保证工程设计精度要求的前提下,采用优化拟合方法[11-15],经多备选函数、多参数逐次搜索逼近,最终择优确定了表达形式简单、计算过程简捷的近似计算通式,可在实际工程设计中推广应用。

1 收缩水深基本计算公式

根据水力学原理,由能量守恒方程获得收缩水深的基本计算公式[16]为

(1)

式中:E0为以过闸(坝)后下游收缩断面底部为基准点的过水建筑物上游总水头,m;hc为收缩断面处的水深,m;Q为过闸(坝)的设计流量,m3/s;g为重力加速度,通常取9.81 m/s2;φ为与过水建筑物类型有关的流速系数;Ac为与收缩水深hc相对应的过水断面面积,m2。

对于抛物线形断面,当方程指数为n时,其断面曲线方程形式为

y=axn(a>0,n>1)

(2)

则其过水断面面积为

(3)

式中:a为抛物线形断面形状参数;n为抛物线指数。

设

(4)

式中:xc为无量纲收缩水深;k为已知综合参数。将式(3)和式(4)代入式(1),进一步整理可得

k=xc(1-xc)n[2(n+1)]-1

(5)

通过式(5)求解出xc后,由式(4)即可求得

hc=E0xc

(6)

2 收缩水深简化通式及其精度分析

2.1 简化通式的建立

(7)

式中:A和β分别为待定系数及指数。

图1 不同n时的xc-k关系曲线

采用数值拟合分析方法[17-18],将目标函数设定为标准剩余差最小,即

(8)

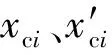
图2 xc-k及关系曲线(n=2)

(9)

式中:B、γ分别为与抛物线方程指数n有关的系数,可由表1查得,当n介于表1中相邻两值之间时,可采用内插法获得。

表1 不同 n时的B、γ值

利用式(9)即可根据已知的k及n求解无量纲收缩水深xc,进而完成收缩水深hc的计算。

2.2 简化通式的精度分析

(10)

式中:zi为数值拟合计算的相对误差,%。

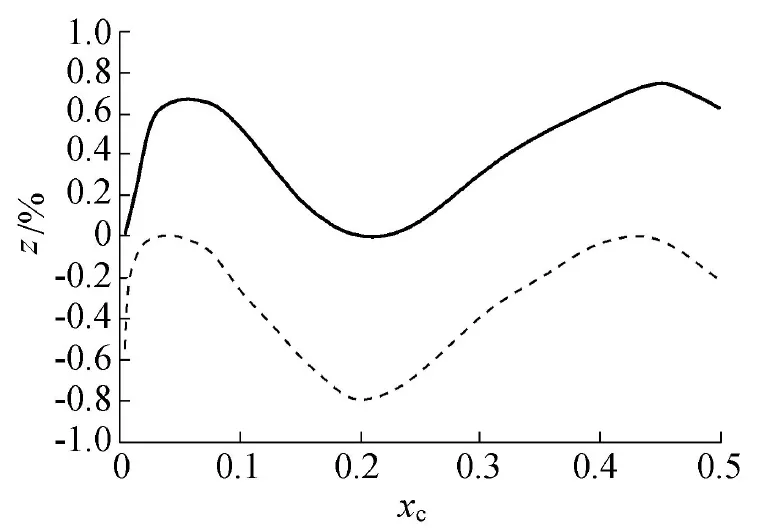
图3 式(9)拟合误差包络曲线

由图3可见,在工程实用参数范围内,用式(9)求解任意抛物线形断面渠道收缩水深的最大相对误差不超过0.755%。由相对误差的分布情况可见,当0.005≤xc≤0.1时,相对误差以正误差为主,最大误差值为0.552%;当0.1

3 简化公式的应用举例

选取文献[4]中的计算实例:已知水库溢流坝坝前断面总水头E0=10.31 m,坝上设计通过流量Q=140 m3/s,流速系数φ=0.95,坝后选用方程为y=0.25x2的抛物线形断面渠道,求坝下断面收缩水深hc的值。

根据已知参数由式(4)求得k=0.239 72,当n=2时,由表1查得B=0.588 6、γ=1.774 5,将k、B及γ代入式(9)可求得xc=0.164 6,再由式(6)求得hc=2.728 m。而由计算机编程求得收缩水深的精确解为2.741 m,相比该精确解,式(9)计算结果的相对误差仅为-0.474%,表明本文提出的简化计算通式(9)具有很高的计算精度。

4 结 语

目前,求解抛物线形断面渠道收缩水深的简化计算公式因方程指数的不同而不同,既不通用又不便应用。本文通过对整理后的高次方程的优化拟合,建立了求解该类断面收缩水深的近似通式,其特点是用一个通式即可完成工程实用范围内各类抛物线形断面渠道收缩水深的计算,解决了现有简化公式仅适用于某种特定抛物线指数方程求解的不足。该简化通式仅用一个正切指数函数表示,形式简单易记,便于工程技术人员实际应用。公式的计算精度较高,经比较,最大相对误差仅为0.755%,可较好地满足工程计算精度要求,可为该类断面渠道正常及共轭水深简化计算通式的建立提供借鉴。

参考文献：

[1] 魏文礼,杨国丽.立方抛物线渠道水力最优断面的计算[J].武汉大学学报:工学版,2006(3):49-51.(WEI Wenli,YANG Guoli.Hydraulic calculation of optimal cross-section of cubic parabola channel[J].Engineering Journal of Wuhan University,2006(3):49-51.(in Chinese)

[2] 张志昌,刘亚菲,刘松舰.抛物线形渠道水力最优断面的计算[J].西安理工大学学报,2002,18(3):235-237.(ZHANG Zhichang,LIU Yafei,LIU Songjian.Paralbola-shaped channel hydraulic calculation of optimal cross-section[J].Xi’an University of Technology,2002,18(3):235-237.(in Chinese)

[3] 文辉,李风玲.立方抛物线断面渠道收缩水深的直接计算方法[J].人民长江,2009,40(13):38.(WEN Hui,LI Fengling.Direct calculation method of contracted depth in semi-cubic parabola-shannel[J].Yangtze River,2009,40(13):38.(in Chinese)

[4] 赵延风,宋松柏,孟秦倩.抛物线形断面渠道收缩水深的直接计算方法[J].水利水电技术,2008,39(3):36-37.(ZHAO Yanfeng,SONG Songbai,MENG Qinqian.Direct calculation method for water depth in parabolic-shaped channel with contracted section[J].Water Resources and Hydropower Engineering,2008,39(3):36-37.(in Chinese)

[5] 芦琴,王正中,任武刚.抛物线形渠道收缩水深简捷计算公式[J].干旱地区农业研究,2007,25(2):134-136.(LU Qin,WANG Zhengzhong,REN Wugang.Formula for quickly calculating water depth at vena contraction in parabola form channel[J].Agricultural Research in the Arid Areas,2007,25(2):134-136.(in Chinese)

[6] 王正中,王羿,赵延风,等.抛物线形断面河渠收缩水深的直接计算公式[J].武汉大学学报:工学版,2011,44(2):175-177.(WANG Zhengzhong,WANG Yi,ZHAO Yanfeng.Formula for direct calculation of contracted depth of parabolic-shaped canal[J].Engineering Journal of Wuhan University,2011,44(2):175-177.(in Chinese)

[7] 文辉,李风玲.抛物线形断面渠道收缩水深的解析解[J].长江科学院院报,2009,26(9):32-33.(WEN Hui,LI Fengling.Analytical solution of water depth in parabolic-shaped channel with contarcted section[J].Journal of Yangtze River Scientific Research Institute,2009,26(9):32-33.(in Chinese)

[8] 冷畅俭,王正中.三次抛物线形渠道断面收缩水深的计算公式[J].长江科学院院报,2011,28(4):29-31.(LENG Changjian,WANG Zhengzhong.Formula for calculation contracted water depth of cubic paraboa cross section [J].Journal of Yangtze River Scientific Research Institute,2011,28(4):29-31.(in Chinese)

[9] 谢成玉,滕凯.三次抛物线形渠道断面收缩水深的简化计算公式[J].南水北调与水利科技,2012,10(1):136-138.(XIE Chengyu,TENG Kai.Simplified equation of contracted water depth in a channel having a cubical parzbola section[J].South-to-North Water Transfers and Water Science & Technology,2012,10(1):136-138.(in Chinese)

[10] 赵延风,王正中,刘计良.抛物线类渠道断面收缩水深的计算通式[J].水力发电学报,2013,32(1):126-131.(ZHAO Yanfeng,WANG Zhengzhong,LIU Jiliang.Explicit epuation for calculation of contracted flow depths in channels of parabolic cross-section[J].Journal of Hydroelectric Engineering,2013,32(1):126-131.(in Chinese)

[11] 刘刚,滕凯.梯形断面均匀流水深的近似计算公式[J].水利与建筑工程学报,2012,10(1):41-44.(LIU Gang,TENG Kai.Approximate calculation formula uniform flow depth of trapezoidal cross-section[J].Journal of Water Resources and Architectural Engineering,2012,10(1):41-44.(in Chinese)

[12] 谢成玉,滕凯.抛物线形断面渠道均匀流水深的近似计算公式[J].水电能源科学,2012,30(7):94-95.(XIE Chengyu,TENG Kai.Approximate formula of uniform flow depth for parabolic cross-section channel[J].Water Resources and Power,2012,30(7):94-95.(in Chinese)

[13] 滕凯.消力池深的简化计算法[J].人民长江,2012,43(15):77-79.(TENG Kai.Simplified calculation method of depth of stilling basin[J].Yangtze River,2012,43(15):77-79.(in Chinese)

[14] 滕凯,周辉.弧底梯形明渠正常水深的简化计算法[J].黑龙江八一农垦大学学报,2012,24(5):85-88.(TENG Kai,ZHOU Hui.A method of simplifying calculations for the normal water depth of open trapezoidal channel with arc bottom[J].Journal of Heilongjiang Bayi Agricultural University,2012,24(5):85-88.(in Chinese)

[15] 滕凯.标准门洞形过水断面临界水深的简化算法[J].华北水利水电学院学报,2012,33(5):1-3.(TENG Kai.Simple computation of critical water depth of standard door-shaped waterway tunnel[J].Journal of North China Institute of Water Conservancy and hydroelectric Power,2012,33(5):1-3.(in Chinese)

[16] 张志昌.水力学[M].北京:中国水利水电出版社,2011.

[17] 王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.

[18] 阎凤文.测量数据处理方法[M].北京:原子能出版社,1988.