三点波源干涉三维图像仿真设计
2014-03-22邝雄
邝雄
(海南师范大学物理与电子工程学院,海南海口571158)
大多数普通物理学教科书中只讨论两点波源的干涉现象,两频率相同、振动方向平行、相位相同或相位差恒定的两点波源的相干涉现象[1],其相干图像的仿真也有相关文章论述[2-5],甚至也有相干图像的立体仿真[6].对于频率不相同、振动方向平行、相位相同或相位差恒定的两点或三点波源(即多点波源)的干涉图象又会如何?在现实生活中,我们是很难观察到这种干涉现象的,在教科书中也很少讨论.利用计算机进行程序设计,可仿真这一干涉图象.本文就讨论如何设计频率不相同、振动方向平行、相位相同或相位差恒定的多点波源的干涉波的仿真图象问题.
1 设计目标
为使设计的程序具有交互性、可控性和可观察性,对设计目标提出几点具体要求:
1)设计的多点波源干涉仿真图中采用三点波干涉方式,即仿真三点波源的干涉图象;
2)设计的三点波源干涉仿真图象必须是立体图像显示方式,以仿真真实的干涉效果;
3)仿真的干涉图像范围要足够大,且仿真范围是可以调整的,以便于观察不同的较大范围内的整体干涉效果;
4)干涉的点波源源点位置是可以改变的,可实现观察波源位置改变时,干涉波形图的变化;
5)点波源的频率(或波长)设置是可以改变的,可实现观察频率(或波长)变化时干涉图的变化;
6)干涉波的时间(或初相)设置是可以改变的,也可实现观察不同时间点(或初相)干涉图情况.
总的要求就是,设计的干涉仿真图,交互性强,基本上可实现人工在线调整.
2 设计思路
要实现三点波源干涉仿真图象设计目标,点波源的振动方式方程是基础.点波源的振动方程可以选用最典型的正弦函数波方式,同时选取非衰减式振动传播方式形成的波动方程.这样,可以容易实现在较大范围内获得稳定的相干波形.
选定点波源的振动为正弦函数方式后,点波源波动方程中至少有四个量需要设置,即振幅、矢径、时间和频率(或波长).在程序设计的算法上,可采用在输入一定的振幅、时间和频率(或波长)时,先计算不同点处(即矢径所指点)多点波源干涉叠加的结果,再将结果送显示控件加以显示的思路.当改变其振幅、时间和频率(或波长)的任一量时,再重新计算显示.采取这一思路,目的是减少程序设计中使用过多的循环结构,影响程序运行速度,同时也简化设计程序.
3 设计平台确定
设计的多点波源干涉仿真图象,要有良好的交互性,就意味着在界面设计中需要较多的交互设置.于是必须设计更多的交互控件.同时为了实现较好的立体图效果,需要的图形显示控件也将复杂,如果采用一般的文本程序语言方式设计,其工作量之大,可想而知.如果采用VB或VC来设计,对控件属性的设置,其复杂性也是不小的.但是采用G语言设计,将会使问题变得简单.因为G语言中有很多类的交互和显示控件,只用对相应控件属性进行少量的设置,直接调用,就可获得良好的效果.G语言程序简洁,使程序设计变简单而易实现[7].因此我们采用G语言中的LabView平台来设计,且采用较新版本的LabView2009版作为设计平台,这将是一种很好的选择.
4 三点波源干涉波仿真图像程序设计
采用LabView2009平台设计三点波源干涉波仿真图像,在程序设计中,有几个需要考虑的关键点:一是立体图像显示方式的设计;二是计算变量的设计;三是算法中对循环结构的设计;四是设计合理的与各点振动波源相关的波动函数控件.
4.1 显示控件设计
设计的三点波源干涉波仿真图像,要实现三维立体图效果,设计的显示控件必须是三维立体显示控件.在LabView2009中,实现三维立体图显示,不需重新设计显示控件,只用直接选取现有的相应控件,对其属性做相应的设置便可实现良好效果.
LabView2009平台中能显示立体图类的控件,就有三维曲面图控件.该控件具有可改变显示模式的特点[8],特别是在显示过程中,该控件显示的三维图像具有很好的可调性,程序运行时,对相干图形的视角和幅度都可以随意调整,这是该控件的主要优点.该控件可以从控件板的图形控件类中选取.
4.2 计算变量设计
设计的三点波源干涉仿真图象程序,可采用在输入一定的振幅、时间和频率(或波长)时,先计算不同点处(即矢径所指点)多点波源干涉叠加的结果再显示.这就要考虑计算变量问题,因干涉空间的每一相干点,都涉及到三点波源的三个矢径变量,可选三个矢径为计算变量,也就是说需要的计算变量至少要有三个.
为统一三个矢径变量,特别是统一计算变量设计中的变化步长,可以采用直角坐标系来标示矢径变量.可用xy平面确定相干点,用z向变量确定点的相干强弱,通过z变量来显示相干强弱的效果图像.程序中相干点的三个矢径变量将变成与三点波源对应的含有z向变量强弱信息的x、y变量,在取变量进行计算时,也很容易实现了统一计算变量中的变化步长.这样,将矢径变量变换为统一的x和y变量表示后,只用选两层循环结构来设计计算程序便可,同时可使设计程序大大简化.
4.3 循环结构设计
根据上计算变量设计,主要计算x、y两个变量,因此程序设计中只用两层循环结构就能实现变量变化计算,对应的变量就是x和y.可采用内层循环对应变量x,外层循环对应变量y方式.算法上可取一定的y值,先设置一循环结构用于计算不同x点的相干值,再设计另一循环结构用于计算不同y值时各x点的值,这就减少了使用循环结构的层数.
在设计循环结构中,只要将x、y变量范围设计为可输入设置方式,也自然实现了显示范围的可设置性.这时的x和y计算变量是有限变量,采用的循环结构也必须是有限循环方式的循环结构.程序设计的LabView2009平台中,可以采用for循环结构来实现有限循环计算.for循环结构控件可从函数选板上编程的结构类控件中选取,它的特点是可以方便地确定循环结构的循环次数,且循环次数可以设计为可交互的输入方式.
4.4 函数设计
函数的设计主要以三点波源的波动方程形式为基础.选定点波源的波动方程为三角函数形式,就必须以三角函数为主函数来设计控件.在Lab⁃View2009平台中,要显示三角函数形式的波形控件,可有多种选择,可选择Express控件中的输入信号控件,也可选择信号分析中的仿真信号类控件,还可以选择函数选板上编程中结构类的公式节点控件等.但是,能简单地和三维立体图显示控件实现数据简便配连的一种控件,是函数选板上,算术与比较控件中数学控件类的三角函数控件.可选取其中的正弦函数来表示三角函数.
点波源波动方程的三角函数并不复杂,主要是确定三角函数的矢径、振幅、时间和频率(或波长)等变量.可采用函数板上三角函数控件类与算术与比较控件中的数值类相应控件,就容易地组合成相应的波动方程.这是相干波图像仿真设计的一种简便方法.用函数板上三角函数等控件类设计,只在组合函数式上花点工夫,而其他设置并不复杂.
4.5 三点源干涉波仿真图像设计程序
依据上设计,用LabView2009平台设计的三点源干涉波仿真图像程序见图1.
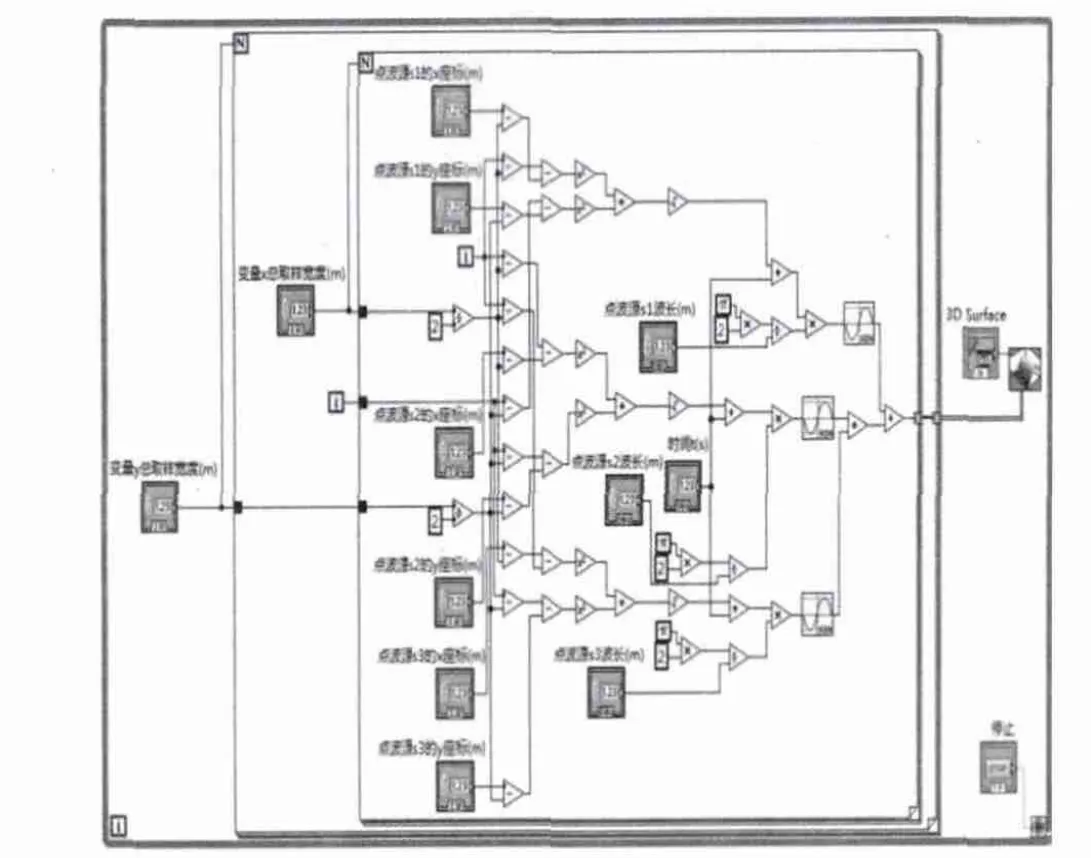
图1 程序设计图Fig.1 Program design diagram
图1中程序采用两层for循环结构,最内层对应x变量,再外层对应y变量,最外层为while循环,是程序的运行控制要求,程序内各函数控件都采用了算术与比较类控件.三维曲面图控件设置于两for循环外,是三维曲面图控件计算属性决定的.
程序相应的前面板见图2.
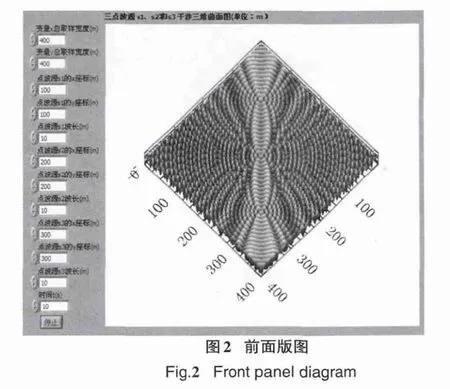
在前面板中,变量x和y的宽度是可以在运行过程中进行设置的,各干涉点波源的波源点位置是可以调整的,可以仿真观察不同点波源位置时的干涉情况.各点波源的初相是可调整的,其波长也是可以调整的,也就是观察宽度、时间和三点波源的位置、波长都是可以调整的,实现了很好的交互性.
5 三点源干涉波图像仿真结果
下面就运行该程序,显示在不同情况下三点源干涉波图像的仿真结果.
5.1 同频率三点源处于同一直线位置时的干涉图形仿真
如图3,就是设置总宽度x和y都为320 m,且取相同波长(即相同频率)下,如取波长为10 m,三点波源分别处于:点波源s1(80 m,80 m)、点波源s2(160 m,160 m)和点波源s3(240 m,240 m),它们相对位置处于同一直线上时的干涉波三维仿真图形,调整为顶正视图,其相干的正顶视图为图4.
5.2 不同频率三点源处于同一直线位置时的干涉图形仿真
同上,取总宽度和三点波源位置不变,各点波源取不同的波长,如取:点波源s1的波长为7 m、点波源s2的波长为18 m和点波源s3的波长为27 m,其相干波三维图像见图5,其相干正顶的视图见图6.

5.3 同频率三点源处于三角位置时的干涉图形仿真
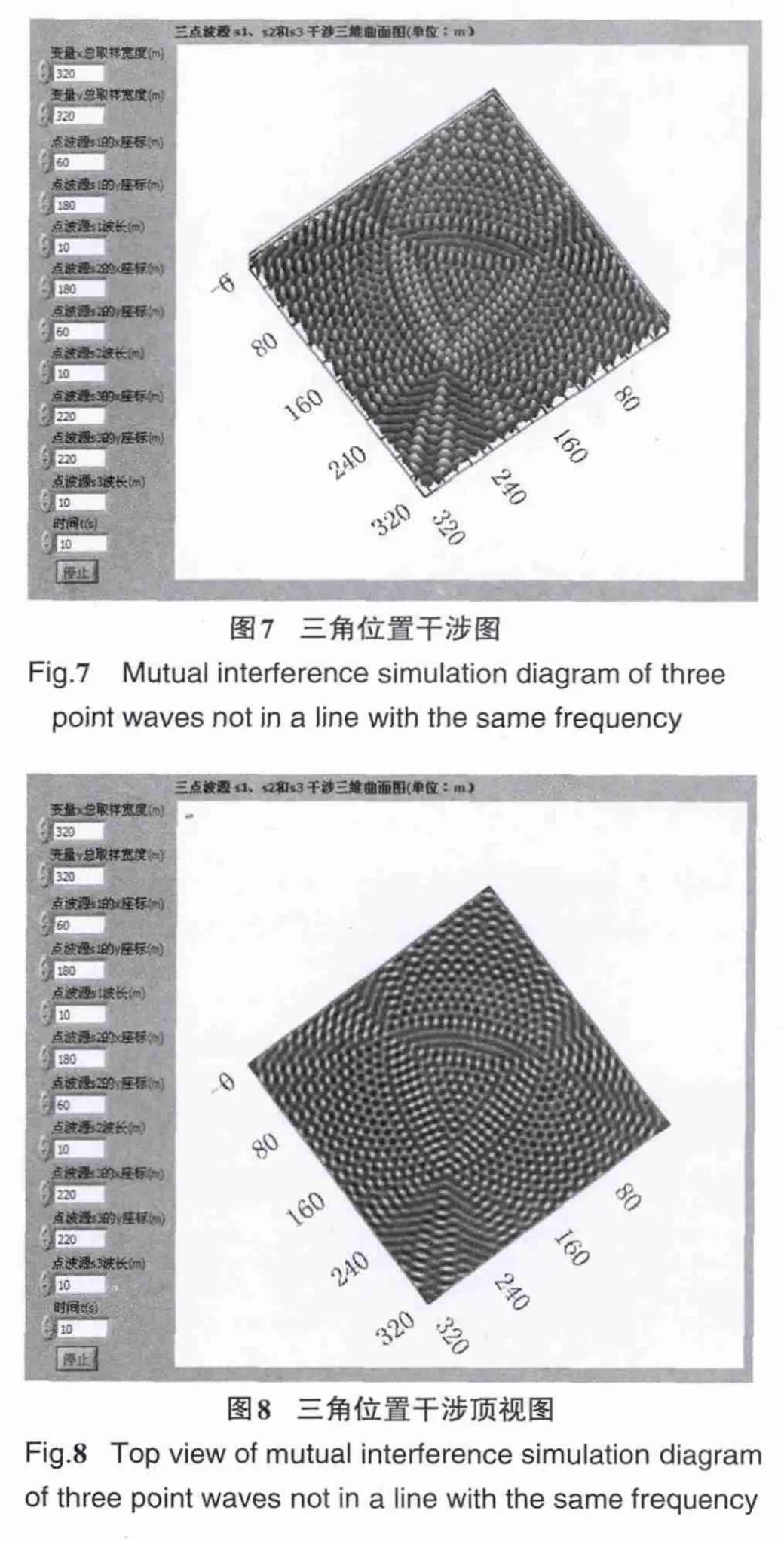
取总宽度不变,且取相同波长(即相同频率)下,但三点波源位置变化.如取波长为10 m,三点波源分别处于:点波源s1(60 m,180 m)、点波源s2(180 m,60 m)和点波源s3(220 m,220 m),三点波源处于三角位置时的干涉图形仿真,其相干波三维仿真图见图7,相干波正顶视图见图8.
5.4 不同频率三点源处于三角位置时的干涉图形仿真
同上取总宽度不变,且三点波源处于三角位置不变,但取点波源不同的波长,如取:点波源s1的波长为5 m、点波源s2的波长为12 m和点波源s3的波长为25 m,其相干波三维仿真图见图9,其相干波正顶视图见图9、图10.

上面就是三点源干涉波三维立体图像的仿真结果,限于篇幅,只是在运行过程中讨论几种情况下的仿真结果,其实还可以设置于不同点波源位置、不同波长、不同时间和不同范围情况下的仿真情况.另外还可以修改设计,设计出四点或更多点波源的干涉情况.
[1] 马文蔚,解希顺,谈漱梅,等.物理学(下册)[M].4版.北京:高等教育出版社,1999:63-66.
[2] 陈琳,朱湘柱.杨氏双缝干涉仿真模型设计[J].计算机仿真,2009,26(9):269-272.
[3] 李晨璞,谢革英,胡金江,等.基于LabVIEW的牛顿环实验动态仿真[J].实验室研究与探索,2013,32(6):97-101.
[4] 陈燕,何松.杨氏双缝干涉实验的MATLAB仿真设计[J].绵阳师范学院学报,2011,150(8):42-45.
[5] 程湘,王准,黄泽安.基于OpenGL的水面波干涉仿真[J].佛山科学技术学院学报:自然科学版,2003,21(1):12-14.
[6] 邝雄.波干涉现象的三维图像仿真设计[J].海南师范大学学报:自然科学版,2012,25(4):389-393.
[7] 张重雄.虚拟仪器技术——分析与设计[M].北京:电子工业出版社,2007:138-139.
[8] 李瑞,周冰,胡仁喜.LabVIEW2009中文版虚拟仪器——从入门到精通[M].北京:机械工业出版社,2010.
