基于重整化群方法的三棱柱单元整体破坏概率模型
2014-03-22顾培英
顾培英,邓 昌,汤 雷
(1.南京水利科学研究院材料结构研究所,江苏 南京 210029; 2.水利部水科学与水工程重点实验室,江苏 南京 210029)
目前,许多混凝土结构承担着生命线工程的重任,其失事所造成的直接、间接经济损失不可估量。我国很多混凝土结构已进入中老年期,往往存在各种损伤与病害。此外,若混凝土结构遭受地震及其他意外事故,局部破坏在所难免,那么局部破坏对整体安全性的影响以及是否会导致整体倒塌等破坏是目前还无法准确回答的问题,所以有必要开展水工混凝土结构整体安全性研究。
混凝土结构损伤状况一般是通过外观破损调查,并借助于多种无损或局部有损专项检测技术来获得,但从某种意义上讲仅依据局部检测结果还难以真正达到整体安全性评价的目的。顾培英等[1]提出了一种基于重整化群理论的混凝土结构整体安全性评价新方法。重整化群方法是美国威尔逊在量子场理论中提出来的,他把量子场论中的重整化群方法应用于临界现象研究,提出重整化群在不动点附近的性质决定了体系的临界行为,建立了相变临界现象理论,这是临界现象研究领域的重大突破,1982年威尔逊也因此获得诺贝尔物理学奖[2-4]。相变基本特点是系统变量连续变化会造成系统宏观参数的不连续变化(突变)。重整化群方法可处理各种相变和临界点问题,其利用了标度不变性,先在最小标度上研究较为简单的相互作用系统,然后将问题重整化,进一步在大的标度下利用同样系统研究大的相互作用系统,过程不断重复[5]。重整化群方法主要有3个方面的应用:①多孔介质中的渗流;②岩石破碎;③断层破裂。
重整化群方法成功地解释了各种相变和临界点问题,得到尺度越来越大情况下的原胞破坏概率递推公式,建立的是局部与整体的关系,该方法已在岩石破碎和断层破裂等方面得到应用[6-16]。由于混凝土与岩石均属脆性材料,性能较为相似,所以可以将重整化群方法“嫁接”到混凝土结构。顾培英等[17]建立了基于小单元、大单元试验结果的混凝土局部损伤概率确定方法,并针对数值仿真成果,提出混凝土局部损伤概率服从二参数的Weibull分布。顾培英等[1]还针对正方体的水工混凝土结构,建立了不等局部损伤概率与整体安全性之间的关系,但一般水工混凝土结构不具备正方体的条件,经常包含斜面或曲面,需分别对结构体和单元体进行处理,建立符合实际水工混凝土结构的整体破坏概率数学模型。
重整化群方法处理大体积块体结构具有优越性,适宜应用于重力坝的整体安全性评价。重力坝基本剖面呈三角形,为适应地基变形、温度变化和混凝土的浇筑能力,用横缝将坝体分隔成若干个独立工作坝段。可将每个坝段作为一个整体加以分析,坝段呈三棱柱体结构,所以需推导三棱柱单元的混凝土结构整体破坏概率,其他斜面或曲面结构可通过等效、补偿处理,综合利用三棱柱单元和正方体单元数学模型得到整体破坏概率。本文在基于正方体单元岩石破碎概率模型的基础上,推导基于三棱柱单元的结构整体破坏概率模型,得到导致结构整体破坏的单元破坏概率临界值,并对实际工程的原胞级数取值进行分析。
1 正方体单元岩石破碎概率模型
根据文献[1,5],正方体单元岩石破碎情况如图1所示。图1中破碎单元用正方体角上的黑点表示,a、b、c、d、e、f分别为某破碎单元数不变情况下的不同组合形式,数字为破碎单元个数,括号内的数字表示出现该破碎情况的次数。图1(n)(q)(s)(t)(u)(v)是6种岩石整体破碎情况。
图1所示的模型假定8个单元的破碎概率相等,用p0表示,分别得出6种情况下各自的破碎概率,并求和, 6种岩石破碎情况下1级原胞破碎概率p1与1级单元破损概率p0之间存在以下关系[1,5]:
(1)
重整化后,可以将同样的方法应用于更高级原胞,将式(1)中的下标1、0替换成n+1、n,有
(2)
如果1级原胞特征长度为2h,则第n级原胞的特征长度为2nh。
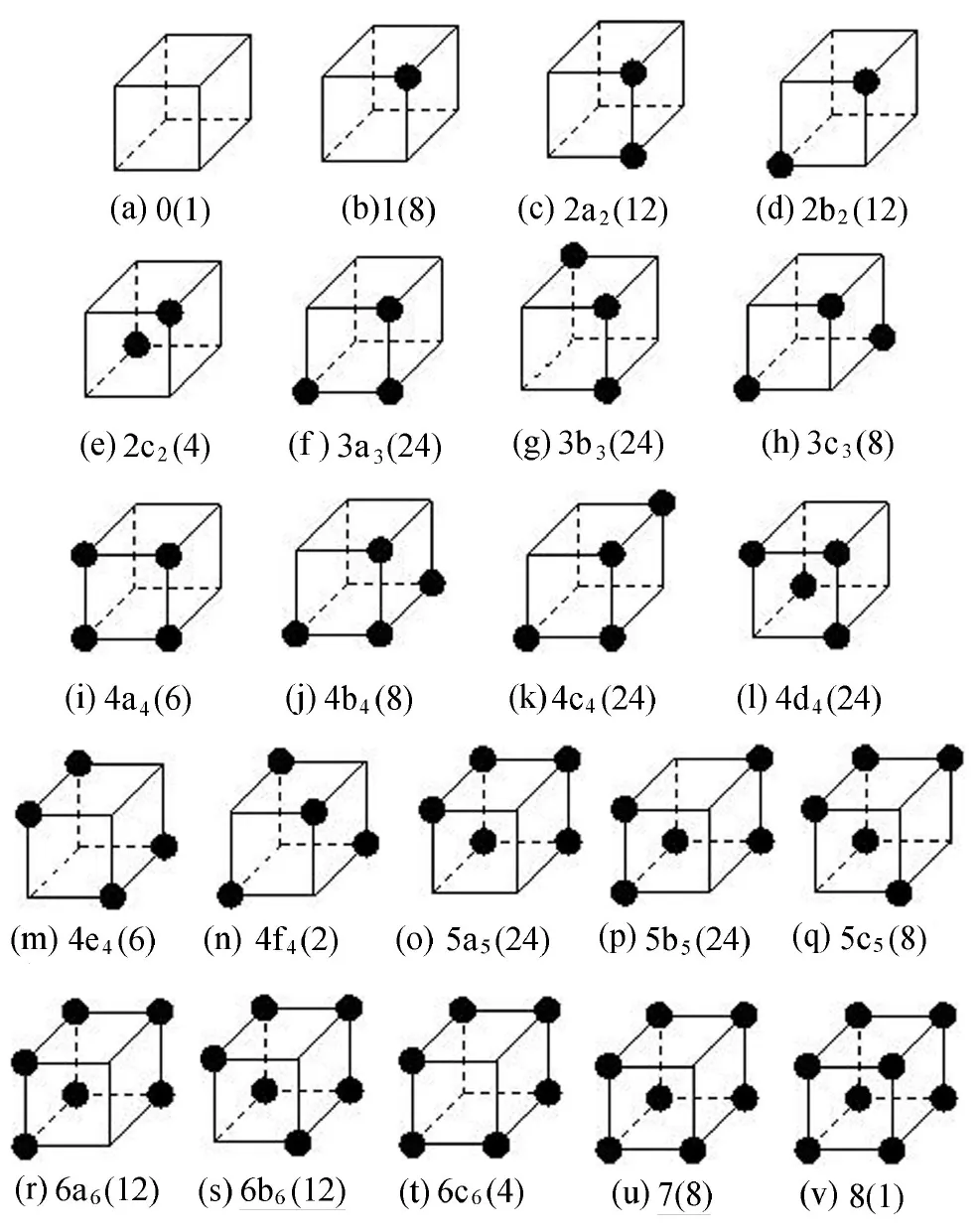
图1 正方体单元岩石破碎情况示意图
2 三棱柱单元混凝土整体破坏概率模型
2.1 公式推导
图2为三棱柱单元混凝土3级原胞三维模型示意图。与正方体单元岩石破碎假设类似[1,5],原胞中每个单元要么破碎,要么完整,如果原胞两面之间有一不破坏的“支柱”相连,则认为原胞是完整的。此模型也是8个单元组成1级原胞,每个原胞破坏状况也有256种情况,去掉重复情况,从拓扑学角度共有36种不同情况,三棱柱单元混凝土破坏情况如图3所示(编号含义同图2)。图3(F)(H)(I)(J)是4种原胞破坏情况。图4为6c6和6d6三棱柱单元混凝土原胞示意图,图4中空白部分表示破坏单元,阴影部分表示完整单元。6c6具有用阴影部分表示的非破坏“支柱”,因而认为是完整的,而6d6任两个面之间没有由完整单元组成的“支柱”支撑,是一个破坏原胞。
图2 三棱柱单元混凝土3级原胞三维模型示意图
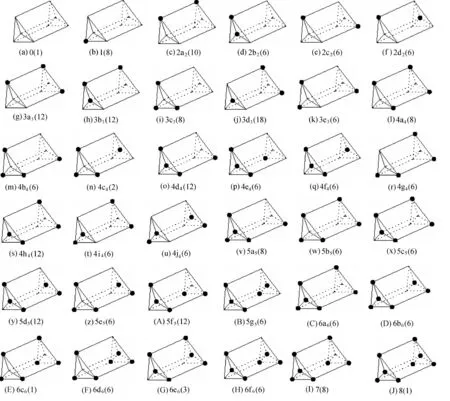
图3 三棱柱单元混凝土破坏情况示意图
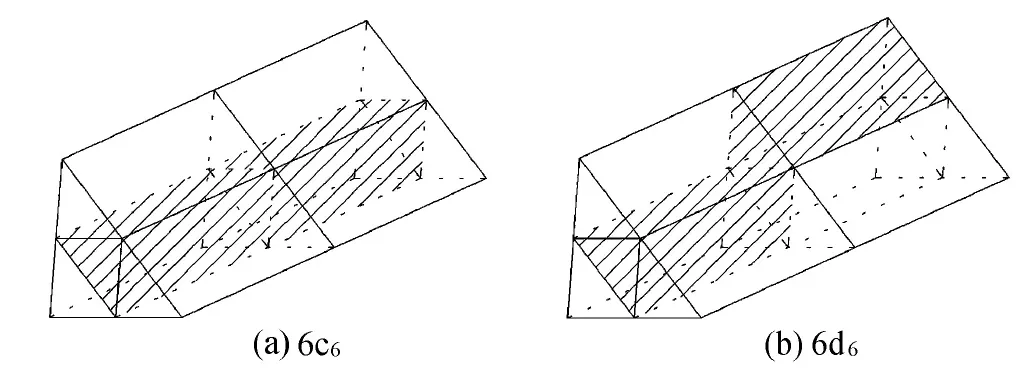
图4 6c6和6d6三棱柱单元混凝土原胞示意图
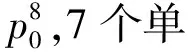
(3)
重整化后,可以将同样的方法应用于更高级数,将式(3)中的下标1、0替换成n+1、n,有
(4)
2.2 不动点分析
图5为基于三棱柱单元混凝土整体破坏概率模型pn+1与pn的关系曲线。为了研究不动点,将式(4)改写成
f(x)=x6(5x2-16x+12)
(5)
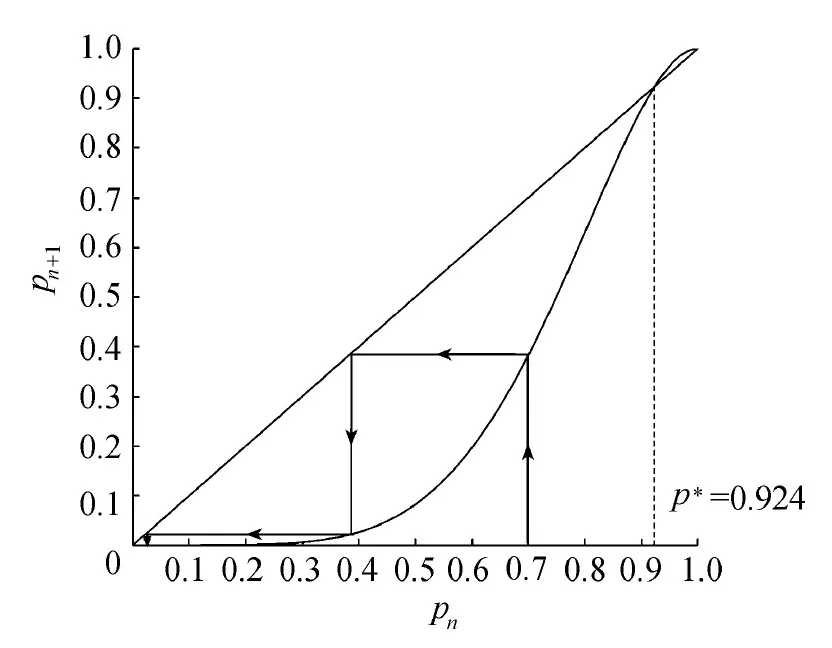
图5 基于三棱柱单元混凝土整体破坏概率模型pn+1与pn的关系曲线
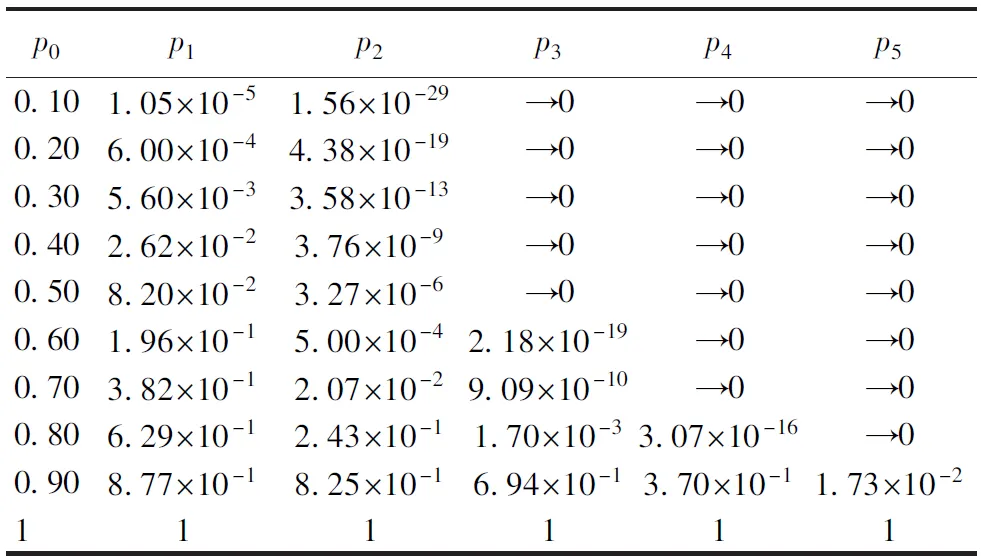
令f(x)=x,可得到不动点。在0 为说明式(4)的迭代过程,考虑一特定情况:当p0=0.70时,由图5可得p1=0.382 4、p2=0.020 7、p3=9.18×10-10,p3接近零,当迭代继续下去时,p∞=0,因此,p0=0.70时不会发生整体破坏。当p0=0.95时,p1=0.964 8、p2=0.981 9、p3=0.995 0,p3→1。p*=0.924是一个临界点,它对应于混凝土发生突变式的破坏。所以,对于小于临界值的概率,即0 若最大级原胞对应于某一有限的三棱柱混凝土结构体,每个单元破坏概率相等且已知,则可通过式(4)递推得到该结构整体破坏概率。理论上讲,原胞级数趋于无穷大,即1级单元尺度远小于最大级原胞尺度时,若单元破坏概率不是临界值p*,则整体破坏概率只有0、1两种可能,即要么破坏、要么完整。但在实际工程应用中,原胞级数不可能取很大,下面对迭代次数进行进一步的分析。表1为三棱柱单元混凝土结构前5次迭代整体破坏概率计算结果。 表1 三棱柱单元混凝土结构前5次迭代整体破坏概率计算结果 由表1可知,当单元破坏概率p0≤0.70时,2次迭代后p2→0;当p0=0.80时,3次迭代后p3→0;当p0=0.90时,3次迭代后p3=0.694 4,5次迭代后p5→0。所以,大多数情况下,只需3次迭代即可获得趋于零的整体破坏概率,这时结构完整,随着p0的增大,收敛速度有所降低;若p0接近于临界值p*时,3次迭代后p3仍较大,利用收敛速度可判断接近临界值的程度。因此,原胞级数即迭代次数取3即可满足实际工程需要。此外,若迭代后整体破坏概率增大或等于1,则混凝土整体发生破坏。 传统重整化群方法只能处理正方体岩石破碎问题,但一般水工混凝土结构不具备正方体条件,本文提出并建立了基于重整化群方法的三棱柱单元混凝土结构整体破坏概率模型。通过不动点计算分析,得到导致结构整体破坏的单元破坏概率临界值。 迭代计算结果表明,大多数情况下,只需3次迭代即可获得趋于零的整体破坏概率,这说明虽然存在局部破坏,但结构整体是安全的。随着单元破坏概率的增大,整体破坏概率收敛速度有所降低。若3次迭代后整体破坏概率仍较大,则说明单元破坏概率接近临界值。若迭代后整体破坏概率增大或等于1,则混凝土整体发生破坏。因此,原胞级数即迭代次数取3可满足实际工程需要。 本文所提出的概率模型适用于重力坝,在确定外载作用下,其局部破坏相应确定,建立了局部破坏概率与整体安全性之间的关系,此模型可从定量的角度评价混凝土重力坝的整体安全性;其他斜面或曲面结构可通过等效、补偿处理,综合利用三棱柱单元、正方体单元概率模型获得结构整体破坏概率。值得一提的是,本文模型是基于等概率三棱柱单元,仍有一些问题有待完善,不等概率三棱柱单元的数学模型推导及其分析成果将另文发表,下一步还将研究外力及其他环境因素对结构整体破坏概率的影响规律。 参考文献: [1] 顾培英,邓昌,汤雷.基于重整化群的水工混凝土结构整体破坏概率研究[J].水利水运工程学报,2010(4):1-5.(GU Peiying,DENG Chang,TANG Lei.Damaged probability of concrete for hydraulic structure based on renormalization group theory[J].Hydro-Science and Engineering,2010(4):1-5.(in Chinese) [2] 于渌,郝柏林.相变和临界现象[M].北京:科学出版社,1984. [3] 陈顒,陈凌.分形几何学[M].北京:地震出版社,2005. [4] 阎贵卿,阎毅.近代数学物理理论计算与可视化技术[M].长沙:国防科技大学出版社,2000. [5] TURCOTTE D L.分形与混沌:在地质学和地球物理学中的应用[M].陈顒,郑捷,季颖,译.北京:地震出版社,1993. [6] SAMMIS C G.Non-linear fracture mechanics model for spallation and coupling of nuclear explosions detonated in hard rock[R].Los Angeles:University of Southern California,1998. [7] LEI Xinglin,NISHIZAWA O,MOURA A,et al.Hierarchical fracture process in brittle rocks by means of high-speed monitoring of ae hypocenter[J].Journal of Acoustic Emission,2005,23:102-122. [8] CHIAIA B,BORRIBRUNETTO M.Multiscale modelling of stick-slip transition of rough (fractal) surfaces[C]//5th International Conference on Processing & Manufacturing of Advanced Materials.Vancouver,Canada:Materials Science Forum,2007:2594-2600. [9] BORRIBRUNETTO M,CARPINTERI A,CHIAIA B.The effect of scale and criticality in rock slope stability[J].Rock Mechanics and Rock Engineering,2004,37(2):117-126. [10] DAVID W F,SCOTT R P.Contamination of silicic magmas and fractal fragmentation of xenoliths in Paleocene plutons on Kodiak Island,Alaska[J].The Canadian Mineralogist,2007,45(1):107-129. [11] WANG Lianguo,WU Yu,MIAO Xiexing,et al.Mechanism of water-inrush from fault induced by mining near the working face[J].Journal of Coal Science & Engineering (China),2007,13(4):393-395. [12] SAHIMI M,REZA R T M,BAHRAMINASAB A,et al.Propagation and localization of acoustic and elastic waves in heterogeneous materials:renormalization group analysis and numerical simulations[J].Acta Mechanica,2009,205(1):197-222. [13] BAHRAMINASAB A,MEHDI V A S,SHAHBAZI F,et al.Renormalization group analysis and numerical simulation of propagation and localization of acoustic waves in heterogeneous media[J].Physical Review B:Condensed Matter and Materials Physics,2007,75(6):1-13. [14] 高召宁,姚令侃,徐光兴.岩石破坏过程的自组织特征与临界条件研究[J].四川大学学报:工程科学版,2009,41(2):91-95.(GAO Zhaoning,YAO Lingkan,XU Guangxin.Study on self-organized characteristics and criticality condition in the course of rock failure[J].Journal of Sichuan University:Engineering Science edition,2009,41(2):91-95.(in Chinese) [15] 吴国雄,丁王飞,张洋,等.沥青混凝土路面开裂破坏的渗流模型分析[J].重庆交通大学学报:自然科学版,2009,28(6):1016-1020.(WU Guoxiong,DING Wangfei,ZHANG Yang,et al.Percolation model of asphalt concrete pavement crack damage[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(6):1016-1020.(in Chinese) [17] GU Peiying,DENG Chang,TANG Lei.Determination of local damage probability in concrete structure[C]//2012 International Conference on Modern Hydraulic Engineering.Nanjing,China:China Association of Hydraulic Engineering Education,2012:489-493.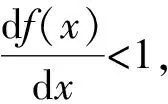
3 原胞级数取值讨论
4 结 语