蜿蜒河流的量规维数与河床演变

汪富泉

(广东石油化工学院继续教育学院,广东 茂名 525000)

蜿蜒河流既具有蜿蜒蠕动的动态特征,又具有迂回曲折的平面形态,所以又称为弯曲河流(本文在研究其平面形态时称弯曲河流,而在研究其演变特征时称蜿蜒河流)。自然界中,蜿蜒河流分布广泛,如中国的下荆江、渭河、南运河、汉江、沅江及辽河等。一方面,适度弯曲的河床能顺导水流,稳定水势,有利于防洪和航运;另一方面,过分弯曲的河床会使水流阻力增大,河床比降减小,阻止洪水宣泄。随着河湾的生长,凹岸不断崩塌,将威胁沿岸城镇人民生命财产安全,严重影响防洪和航运。因此,无论是从兴利还是除害的角度,都有必要研究蜿蜒河流平面形态的结构特征、形成机制及演变规律。

Nikora等[1-2]认为,河流的平面形态由地貌齐性河段(MHRS)决定且受到很多独立因素的控制。描述MHRS的传统参数是各个河湾(宏观形态)参数的平均值。当MHRS由不同尺度的河湾组成且河湾的几何形态随位置高度而变化时,平均值描述方法的意义是不明确的。Nikora等[3]研究了MHRS平面形态的分形结构,从现存地形图上测量计算了位于Moldavia 46个河段的分形维数(盒维数)D,D可以用来描述MHRS的平面形态。河流平面形态在小尺度下呈自相似性，而在大尺度下呈自仿射性[4],辫状河流平面形态具有较好的自仿射性,可用自仿射物体的分形标度指数表征[5]。对于蜿蜒河流,笔者[6-7]研究了下荆江河道的分形特征并探讨了河湾形态演变的自组织性及其稳定性。近年的研究发现,山区河流崎岖地带的地貌也可用D描述[8],说明D可能是更好地反映河流平面形态内部结构的新参数。

已有的研究成果在帮助人们直观形象地认识河流平面形态复杂性方面较有意义,但是,河流是一个开放的复杂非线性耗散系统[6],其平面形态是系统演化的产物。河型的塑造是一个长距离、长时间的过程,人们揭示的分形结构只是演化过程中的一种暂态结构[6]。因此,河流平面形态的分形研究应考虑河流平面形态的分形维数或标度指数是否随时间变化、随时间变化的规律等与河床稳定性密切相关的问题。这些问题比分形维数或标度指数的计算远为困难却被研究者们长期忽略。本文对这些问题进行了初步探讨。

1 弯曲河流的量规维数及计算方法

弯曲河流的平面形态指河流轴线(或中心线)的平面形态。弯曲河流的平面形态可看成一条Jordan线,即曲线没有自交点,视为闭区间[a,b]的拓扑象[9]。 设曲线C的参数方程为

C:r(s)={x(s),y(s)}

式中：s为自然参数。用一个圆规沿着这条曲线测量,设圆规两脚间的距离为δ,测点为x0,x1, …,xm,则

xk-xk-1=δ(k=0, 1, …,m)

(1)

设M(δ,C)表示圆规两脚间距离为δ时沿C得到的测量步数,则M(δ,C)δ可看成用长为δ的码尺测量C时得到的长度。若C是一条直线,则M(δ,C)δ不随δ的改变而改变,因此M(δ,C)∝δ-1。当δ→0时,令ds=dδ表示弧微分,则C的长度L(C)是一个有限常数:

(2)

(3)

为从实测数据得到Ddiv,将式(3)改写为

lnM(δ,C)=A-Ddivlnδ

(4)

其中A=DdivlnL0

若沿C测量时改变码尺δ的长度,在一系列码尺长度{δj:j=1, 2, …，m}下测得对应步数{Mj=M(δj,C):j=1, 2, …，m}。由式(4)进行线性回归,如果从{(lnδj, lnMj):j=1, 2, …，m}计算出的相关系数r能通过置信水平α=1%的临界值检验(因相关系数检验标准较松,所以本文对信度要求较高),则式(3)和式(4)在统计意义下成立,C具有统计自相似性,Ddiv就是C的量规维数。

考虑到一条蜿蜒河流的不同河段可能具有不同的演变特征,可把一条蜿蜒河流分成n个河段,计算各个河段的量规维数{Ddiv,i:i=1, 2, …,n}。其平均值和标准差为

(5)

(6)

维数计算可使用长度M(δ,C)δ,也可使用测量步数M(δ,C)。下面证明Ddiv是一种Housdorff维数。对式(7)进行量纲分析

L=L0ε1-Dh

(7)

式中：Dh为Housdorff维数。令[L]=[L0]=1,知[ε]=0,即若L、L0为欧氏长度,则ε为标度(无量纲量)。因δ是码尺,所以δ=εL0([δ]=[ε]+[L0]=1)。则分形曲线长度公式为

(8)

Ddiv=lnM(δ,C)/ln(L0/δ)=ln(L/δ)/ln(L0/δ)=Dh

(9)

可见,Ddiv与Housdorff维数Dh相同。因量规维数不需要计算曲线长度,因此计算更简便。

2 下荆江河道的量规维数与河床演变

下荆江起于藕池口,止于城陵矶,现河道(2012年)长约170 km[11]。其平面形态蜿蜒曲折,素有“九曲回肠”之称。每年汛期,该河段的防洪都要付出极大代价。在1998年长江全流域特大洪水期间,石首以下江段,北门口、调关矶头等处险情不断,是抗洪任务最艰巨的河段。谢鉴衡等[12]给出了下荆江近500年间的5次平面变化,见图1。由图1可见,整个河段和单个河湾的变化都十分显著。现河道与1975年河道相比,在1∶615 000的地形图上变化较小。

1.新厂;2.袁家埠;3.天星洲;4.藕池口;5.街河;6.石首;7.大公湖;8.孙家峡;9.调弦口;10.八十丈;11.南河口;12.章华港;13.塔市驿;14.青泥弯;15.监利;16.新市街;17.铺子湾;18.下车弯;19.砖桥;20.东港湖;21.洪水港;22.李家墩;23.尺八口;24.老荆河;25.长江故道;26.熊家洲;27.孙梁洲;28.黄泥套;29.老河;30.城陵矶图1 下荆江平面形态变化

笔者用本文方法计算下荆江河道平面形态的特征值,资料采用1∶615 000的实测河道地形图进行计算,研究区域为藕池口至城陵矶,量规的初始间距为3.08 km,最大间距86.24 km。将后一间距取成前一间距的倍数或采用其他非等间距计算得到的结果进行误差分析,相对误差均小于5%,计算结果见表1(表中CB=L/L0为曲折系数)。经检验,在α=1%下lnM(δ,C)和lnδ线性关系十分显著。

表1 下荆江平面形态特征及相关参数

需要指出的是,目前多数学者用数盒子法[13]计算河流的分形维数,其数值结果和采用量规维数所得结果可能有一些差异。如,罗郧等[14]用数盒子法计算了下荆江1869年、1912年、1934年、1952年、1973年等5个年份河道南岸和北岸岸线的分形维数,南岸在1.08～1.22之间,北岸在1.15～1.23之间,北岸1869年为1.19,1952年为1.23,裁弯以后,1973年北岸由1.23减小到1.19,南岸由1.22减小到1.08。而本文结果1959年为1.30,裁弯后1975年减小到1.18(见表1)。对比可见,本文的结果是比较合理的。

从表1可见,在不同时期,下荆江平面形态都具有很好的统计自相似性,分形结构存在的内外尺度分别为δc=0.6 km和Δc=86 km,与Nikora提出的a1B和c1B0基本一致[1]。从计算结果可见,各时期河道中心线的曲折系数、分形维数均随时间变化而波动,说明河流在未受到控制时,由于内外部因素的作用,其发展演化遵循“形成→发展→裁直……”这种循环往复的模式。分形维数增大的过程,即凹岸不断冲刷,凸岸不断淤积,河流向弯曲方向发展的过程,同时也是河床耗散水流能量和增加分形维数的过程。当河湾弯曲到一定程度时,河床平面形态与水流、泥沙输移不适应,就可能发生自然裁直,相当于水流从河床回收能量,使分形维数减小。可见,分形维数的增减反映了水流的能量耗散,或河床与水流交换能量的一种准周期过程。因此,河床平面形态的分形结构及其演化,揭示了河床演变的一种自组织原则。

由图1可见,下荆江不同河段演变特征不同,藕池口—调弦口和调弦口—砖桥段河湾振幅变化差异较大,砖桥—城陵矶段河湾蠕动较大。为定量探讨下荆江河道的变化特征,将其划分成3段:藕池口—调弦口、调弦口—砖桥以及砖桥—城陵矶,其量规维数及曲折系数见表2,统计特征见表3。

从表2和表3可以归纳出如下结论:

表2 下荆江局部河段量规维数、相关系数与曲折系数

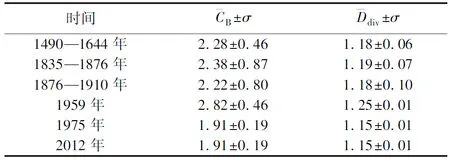
表3 局部河段各时期曲折系数与量规维数的统计特征

a. 同一河湾量规维数和曲折系数的增减趋势可以不一致。 如调弦口—砖桥河段,在1910—1959年间,量规维数增加而曲折系数减小。究其原因,1876—1910年河段平均振幅10.84 km,1959年减小到9.84 km,河湾个数也有所减小,但是河湾形态折叠成“Z”字形。 在1835—1876年、1876—1910年和1959年,藕池口—调弦口河段平面形态相似,河湾个数基本相同,其量规维数差异很小。但是,1876—1910年的曲折系数远小于其余两个时期。其原因可能在于1876—1910年各河湾振幅明显减小。量规方法是把多个尺度(曲折系数涉及的是两个极端尺度)下测量的结果映射为一个不变量——量规维数,量规维数和曲折系数可以互补,但量规维数能更好地描述蜿蜒河段的内部结构。

b. 从空间变化看,1910—1959年各河段的量规维数均增大(注:藕池口—调弦口1910年量规维数为1.256,1959年增大到1.258,保留两位小数时均为1.26)。究其原因,这一时期,河道的弯曲程度和河湾摆幅均有所增加,而1959—1975年和2012年(现河道),各个河湾的量规维数均减小,原因在于1967年与1969年分别对中洲子和上车湾实施了人工裁湾,1972年沙滩子河湾又发生了自然裁直,使下荆江长度减小约80 km,其余时期,各河段的空间变化不均匀,量规维数的增减趋势不一致,特别是1876—1910年各河段平均形态的量规维数差异最大,标准差为0.1,相对涨落(标准差与均值之比)为0.085,曲折系数相对涨落的最大值为0.366,砖桥—城陵矶河段则发生了自然裁直,使河段由弯曲型转变为微弯型,其量规维数仅为1.07。可见,各河段平面形态的变化均可由量规维数定量地反映出来。

c. 从时间变化看,砖桥—城陵矶河段量规维数变化最大,标准差为0.08,其原因与该河段尺八口河湾的蠕动密切相关,该河湾的位置与平面形态在几十年内就可以发生显著的变化[7,11]。 藕池口—调弦口河段的位置及平面形态变化较复杂,裁弯和弯道发展的过程交替演进。调弦口—砖桥河段也出现多次裁弯,但其变化程度比前两者小,维数标准差也最小。可见,由不同时期的量规维数组成的集{Ddiv,ti：i=1,2,…,n}(维数谱)可以定量地反映蜿蜒河流平面形态的演变特征。

3 结 论

a. 首次引入量规维数表征蜿蜒河流平面形态的内部结构,对下荆江河道500多年的平面变化进行分析计算,结果表明,量规维数随时间变化而波动,说明河床形态不稳定,在发生裁弯时,量规维数将由大突然减小,临界维数在1.3左右,差值在0.1左右。如1959年的量规维数为1.3,1967年、1969年和1972年发生人工和自然裁直,1975年减小到1.18。可见,量规维数的谱可以定量描述河段蜿蜒形态“形成→发展→裁直→……”的周期振荡规律。因此量规维数是描述河床形态结构及其演变有效的宏观参数。

b. 对河床的曲折系数、量规维数及其随时间的变化进行了比较分析,结果表明,曲折系数及其变化不能完全反映河道的蜿蜒特征及其演变情况,量规维数可以和它互补，且能更深刻地描述河道平面形态的内部结构及其演变特征。

c. 在河流动力学中,从单个水团、单颗泥沙的运动到一条河流的演变跨越了多个尺度。宏观尺度上的若干系统，如河湾、河段、河床、河流等，都是开放系统,处于非平衡状态和永恒的发展之中,水沙变化过程对蜿蜒河道演变存在显著影响[15],目前对水沙变化的分形特征已有一些初步探讨[16-17]。

参考文献：

[1] NIKORA V I.Fractal structure of river plan forms[J].Water Resources Research,1991,27(6):1327-1333.

[2] NIKORA V I,SAPOZHNIKOV V B,EVER D.Fractal geometry of individual river channels and its computer simulation[J].Water Resources Research,1993,29(10):3561-3568.

[3] NIKORA V I,SAPOZHNIKOV V B.River network fractal geometry and its computer simulation[J].Water Resources Research,1993,29(10):3569-3575.

[4] SAPOZHNIKOV V B,FOUFOULA-GEORGIOU E.Study of self-similar and self-affine objects using logarithmic correlation integral[J].Journal of Physics A:Mathematical and Theoretical,1995,28:559-571.

[5] SAPOZHNIKOV V B,FOUFOULA-GEORGIOU E.Self-affinity in Braided Rivers[J].Water Resources Resecarch,1996,32(5):1429-1439.

[6] 汪富泉.泥沙运动与河床演变的分形特征与自组织规律研究[D].成都:四川大学,1999.

[7] 汪富泉,曹叔尤,丁晶.河湾形态演变的自组织及其稳定性[J].水科学进展,2001,12(1):7-16.(WANG Fuquan,CAO Shuyou,DING Jing.Self-organization and stability of form evolution of river bends[J].Advances in Water Science,2001,12(1):7-16.(in Chinese)

[8] VEENA J,DEVIDAS T,GORAKH D.Geomorphometry and fractal dimension of a riverine badland in Maharashtra[J].Journal of the Geological Society of India,2009,73(3):355-370.

[9] 汪富泉,李后强.分形几何与动力系统[M].哈尔滨:黑龙江教育出版社,1993.

[10] MANDELBROT B B.The fractal geometry of nature[M].New York:W H Freeman,1982.

[11] 钱宁,张仁,周志德.河床演变学[M].北京:科学出版社,1987.

[12] 谢鉴衡,丁君松,王运辉.河床演变及其整治[M].北京:水利电力出版社,1990.

[13] 江齐英,牛瑞卿.长江三峡库岸几何形态的分形分维研究[J].人民长江,2010,41(9):42-44,103.(JIANG Qiying,NIU Ruiqing.Research on fractal and fractional dimension of three georges reservoir bangk’s geometric shape[J].Yangtze River,2010,41(9):42-44,103.(in Chinese)

[14] 罗郧,黄长生.长江下荆江段分形学特征与河道演化[J].现代地质,2011,25(4):808-812.(LUO Yun,HUANG Changsheng.Fractal characteristics and watercourse evolution of the Lower Jingjiang segment in middle Yangtze River[J].Geoscience,2011,25(4):808-812.(in Chinese)

[15] 假东东,邵学军,蒋海峰,等.水沙调节后荆江典型河道横向调整过程的响应Ⅱ：上下荆江调整差异初探[J].水科学进展,2013,24(2):205-211.(JIA Dongdong,SHAO Xuejun,JIANG Haifeng,et al.Responses of channel migration to changes of flow and sediment regime in the Lower Jingjiang reach of the middle Yangtze River Ⅱ:differences between upper and lower sections[J].Advances in Water Science,2013,24(2):205-211.(in Chinese)

[16] 钟亮,许光祥.曼宁公式分形细化初步研究[J].泥沙研究,2013(1):34-38.(ZHONG Liang,XU Guangxiang.Preliminary study of fractal refinement of Manning’s formula[J].Journal of Sediment Research,2013(1):34-38.(in Chinese)

[17] 钟亮,许光祥,曾锋.沙波阻力分形表征的定床试验研究[J].应用基础与工程科学学报,2013,21(1):116-126.(ZHONG Liang,XU Guangxiang,ZENG Feng.Immovable bed experiment study on the resistance of sand wave characterized by fractal dimension[J].Journal of Basic Science and Engineering,2013,21(1):116-126.(in Chinese)