Muskingum法的发展及启示
2014-03-22芮孝芳
芮孝芳,张 超
(1.河海大学水文水资源学院,江苏 南京 210098; 2.河海大学土木与交通学院,江苏 南京 210098)
据记载,洪水演算问题为Graff于1833年首先提出,但遗憾的是Graff并未给后人留下具体的洪水演算方法[1]。直到20世纪30年代中期,美国陆军工程师团在修建位于Colorado河的一项水利工程时,才由McCarthy提出了一个至今仍风靡世界的洪水演算方法,因这个方法首先使用在Colorado河支流Muskingum河的洪水演算中,故后人将其命名为Muskingum法[2]。
McCarthy之所以能提出Muskingum法,笔者认为有其必然性,也有其偶然性。水量平衡原理早在17世纪就在水文学中确立,至McCarthy所处的时代已达到了深入人心的地步,但河段水量平衡方程包含了河段下断面出流量和河段槽蓄量两个未知项,仅根据河段水量平衡方程显然是不可能解决洪水演算问题的。McCarthy当时作出了一个假设:如果能找到既能与同时刻河段槽蓄量呈单值关系,又能根据河段上断面入流量和下断面出流量确定的“另一个流量”,那么问题就可以迎刃而解。实践证明,这个假设在一定条件下居然成立。必然性与偶然性相结合就造就了洪水演算的Muskingum法。
Muskingum法的成功引起了水文学家的研究兴趣。自20世纪30年代以来,水文学家对Muskingum法的研究主要集中在槽蓄方程的构建和所含参数的物理意义上。这场学术讨论,参与度之广,持续时间之长,在水文学发展史上十分罕见,令人称奇。
1 经验解释时期
经验解释时期大体上从1934—1956年,研讨的问题主要是对Muskingum法槽蓄方程的理解和确定其中参数的方法。因为这一时期基本上围绕着McCarthy创建Muskingum法的思路进行研讨,所以也可称为McCarthy-Muskingum法时期。
1.1 对槽蓄方程的理解
McCarthy设想在洪水波运动情况下,河段槽蓄量由“柱蓄”和“楔蓄”两部分组成(图1)[2]。“柱蓄”是相应于河段下断面出流量O的河段槽蓄量,在图1中形似柱体,因此而得名。“楔蓄”是相应于河段上断面入流量I与其下断面出流量O之差的河段槽蓄量,在图1中形似楔体,因此而得名。McCarthy假设“柱蓄”和“楔蓄”的计算式分别为W柱=KO和W楔=Kx(I-O),其中K为蓄量系数,x为与楔体形状有关的系数。这样,河段槽蓄方程就可写成:
W=K[xI+(1-x)O]
(1)
在式(1)中,[xI+(1-x)O]是以x为I的权重和以1-x为O的权重的河段加权平均流量,是河段上、下断面流量的线性组合,因为通过选择x值可能使其与河段槽蓄量呈一一对应的单值关系,所以称其为示储流量,用Q′表示。
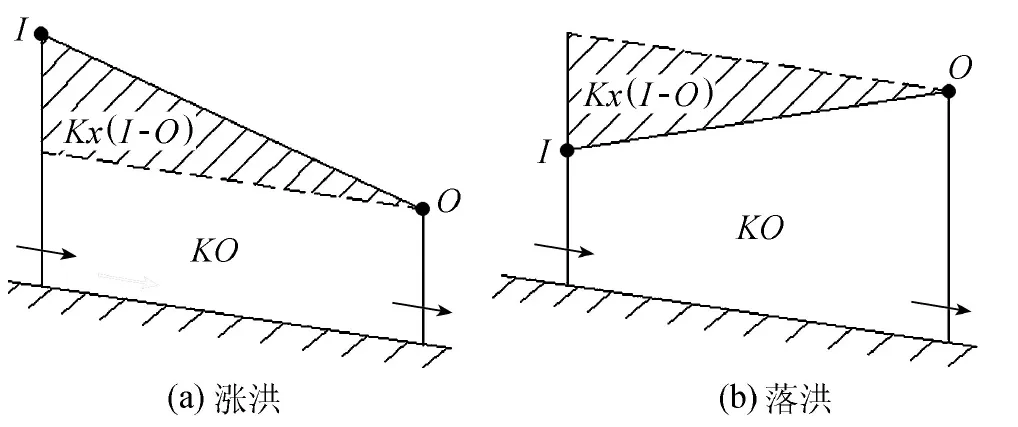
图1 “柱蓄”和“楔蓄”
Linsley等[3]曾试图用水力学知识来解释槽蓄方程,因为槽蓄量W与水位一般具有抛物线型的单值关系。如果假设水位与流量也具有抛物线型的单值关系,那么就可以导得槽蓄量W与流量Q具有下列抛物线型关系:
W=aQm
(2)
式中:a、m分别为经验系数和指数。
如果分别以河段上断面入流量I和下断面出流量O计算河段槽蓄量,那么由式(2)就有:
(3)
Linsley等认为,只要不是洪峰或洪谷处在河段中,河段的槽蓄量W应在WI与WO之间,且W应是WI与WO的加权平均。令权重分别为x和1-x,则有:
W=a[xIm+(1-x)Om]
(4)
对于天然河道,m一般近似为1。在式(4)中,若取m=1,并将a换成K,则结果与式(1)完全相同。
无论是McCarthy的解释,还是Linsley等的解释,都认为x是一个权重,其取值可以在0~1之间。但这一时期的大量实践却并未发现有x>0.5的情况, “对大多数河流来说,x在0~0.3之间,平均接近于0.2”[3],这是为什么?
1.2 参数确定方法
根据McCarthy构建河段槽蓄方程式(1)的基本思路,只要式(1)成立,就一定可以找到一个x,使示储流量Q′与河段槽蓄量W呈单值线性关系。这种直观的想法就导致了确定参数x和K的试错法[3]。试错法常常给人以计算繁复之感觉,为避免这一点又提出了图解分析法和最小二乘法。
图2为根据河段上、下断面实测流量资料得到的以河段上断面入流量I为参变量的河段槽蓄量W与其下断面出流量O的关系,称为经验槽蓄曲线[4],据此确定Muskingum法参数的方法就称为图解分析法。事实上,由式(1)容易得到:
(5)
(6)
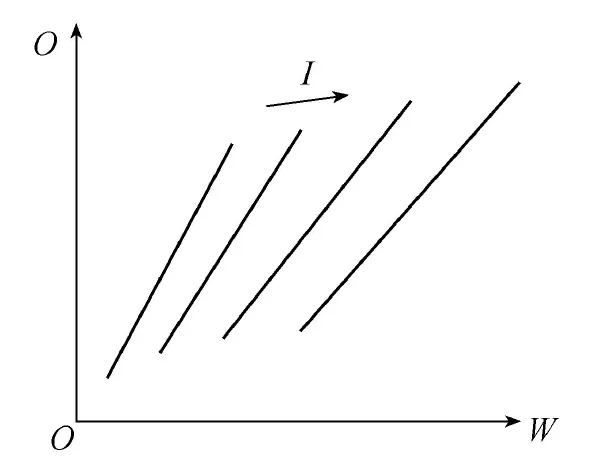
图2 经验槽蓄曲线
最小二乘法是一种基于离差平方和最小的思路构建的推求Muskingum法参数的解析法。以由式(1)计算的槽蓄量与由实测资料求得的槽蓄量的离差平方和最小作为拟合准则,以河段水量平衡方程作为约束条件,可得确定x和K的公式[5]分别为
(7)
(8)
式中:Ii、Oi、Wi分别为第i时刻实测的河段上断面入流量、下断面出流量和相应的槽蓄量;n为时段数。
上述确定Muskingum法参数的方法对实测资料的依赖性很强,这就会产生一个问题:由于在暴雨洪水期间,河段的区间入流一般是不可避免的,因此,它必将作为一种外因对河道洪水波运动规律起着干扰作用,如果对此处理不合理,那么就无法得出合理的x和K。对图3(图中W使用的单位是行业通用单位)所示的Q′-W关系[6],之所以无论x取何值,Q′-W都不可能趋于单值关系,就是因为区间入流难以合理处理。实践证明,区间入流比重越大,这种情况就越易出现。如果区间入流可全部实测,这种情况一般就不会出现了。

图3 沅陵—王家河河段1970年9月一次洪水的Q′-W关系
2 特征河长解释时期
特征河长解释时期大体从1957—1967年,研究的问题主要是建立水文学的槽蓄理论和揭示Muskingum法参数与特征河长的关系。因为这一时期主要是围绕着Kalinin和Milyukov创建的特征河长的基本理论进行的,所以也可称为Kalinin-Muskingum法时期。
2.1 中国的实践
20世纪50—60年代,中国水文科学家和工程师在使用Muskingum法的大量实践中发现[7]:①同一条河流,在河段长大致相同的情况下,上游河段的x一般比下游河段的x大。例如西江南宁—横县河段,河段长163 km,得x=0.30;而位于其下游的梧州—高要河段,河段长160 km,得x=0.05。②河底比降相同的河段,长河段的x大于短河段的x。例如松花江佳木斯—富锦河段,河段长191 km,河底比降1/10 000,得x=0.35;赣江吉安—峡江河段,河段长66 km,河底比降1/10 000,得x=0.25。③河段长相同,河底比降大的x大于河底比降小的x。例如永定河青白口—三家店河段,河段长53 km,河底比降31.9/10 000,得x=0.49;新沂河障山—沐阳河段,河段长50 km,河底比降2.5/10 000,得x=0.45。④有大支流汇入的河段,x一般都比较小。例如钱塘江罗桐埠—芦茨埠河段,河段长51 km,河底比降0.25/10 000,河段中间有大支流汇入,得x=0;伊洛河龙门—黑石兰河段,河段长57 km,河底比降0.3/10 000,河段中有大支流汇入,得x=0.10。⑤有些河段,x必须为负。例如长江万县—宜昌河段,河段长318 km,河底比降2.7/10 000,在三峡建库前x=-0.60。
上述中国水文学家和工程师在实践中发现的问题,显然无法从McCarthy和Linsley等对Muskingum法的经验解释中寻找到答案。
2.2 x与特征河长的关系
正当人们感到“山重水复疑无路”的时候,是Kalinin和Milyukov[8]发现的“特征河长”拨开了迷雾,又在人们眼前出现了“柳暗花明又一村”的美景。1958年Kalinin和Milyukov利用水力学知识导出了如下特征河长l的表达式:
(9)
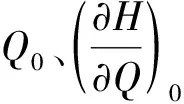
笔者认为,特征河长的发现对水文学有多方面的重要意义,其中所开创的构建槽蓄方程的理论途径最值得称道。根据特征河长的物理意义,如果河段长L正好等于特征河长l,则河段槽蓄量W与特征河段出流量Ol呈单值函数关系,而且在多数情况下,可将此单值函数关系视作如下近似线性函数关系:
W=KlOl
(10)

式中:Kl为洪水波在特征河长内的传播时间;c为洪水波速。
由于Muskingum法的示储流量Q′也与河段槽蓄量呈单值线性关系,因此,只要找到使Q′=Ol的条件,就可对Muskingum法作出一定的物理解释。水文学家从不同的角度证明这个条件[4,7]就是:
(11)
式中:L为河段长。
由式(11)可知:①对一定的河段长L,当i0→∞时,由于l→0,因此x=0.5;当i0→0时,由于l→∞,因此,x<0;当i0在0~∞之间时,由于l在∞~0之间,所以x≤0.5。②对不同的L与l关系,若L>l,则x在0~0.5之间;若L=l,则x=0;若L 图4 1968年8月洪水王家河站计算与实测流量过程线 (12) 其中A=C1+C0C2 C0+C1+C2=1 笔者曾使用Z-变换和留数定理对连续演算Muskingum法的汇流系数做了推导,得到了与上述相同的结论[7]。 水力学解释时期大体上从1967年至今。河道洪水波运动在水力学上属于缓变不恒定流运动,描写其运动规律的方程式早在1871年就由St.Venant导出,后人称之为St.Venant方程组。所谓Muskingum法的水力学解释就是揭示Muskingum法与St.Venant方程组的关系,开此先河者为Dooge,但为此作出关键贡献的是Cunge。所以这一时期也可称为Cunge-Muskingum法时期。 1967年,Dooge[12]通过比较线性化的完全St.Venant方程组的响应函数和Muskingum法的响应函数的各阶累积量,得到了Muskingum法参数x、K和特征河长l的表达式分别为 (13) (14) (15) Dooge根据完全St.Venant方程组线性化形式也导出与式(11)完全相同的结果,这无疑是对Kalinin和Milyukov结论的有力支持,但却带来了一个新问题:为什么在Dooge的推导中,无论特征河长l,还是Muskingum法参数x均与表征流态的弗劳德数有关?为什么当流态为F0>2的急变流时,x、l均出现不合理,以致Muskingum法已不再适用了? 1969年,Cunge[13]发表了一篇题为“关于洪水传播计算方法(Muskingum法)问题”的著名论文,报道了他在使用四点带权显式差分格式推求运动波方程数值解时的有趣发现:如果解的一阶截断误差正好等于扩散波的扩散系数,那么所得到的运动波方程式的差分解不仅具有与McCarthy-Muskingum法完全相同的演算公式形式和完全相同的演算系数的表达式,而且还变成了扩散波方程的二阶精度差分解,条件仅仅是要求满足: (16) 式中:D为扩散波的扩散系数;c为波速;Δx为河段长。 笔者[9,14]曾导得特征河长l与扩散系数D的关系为 (17) 将式(17)代入式(16)得到的x表达式也与式(11)完全相同。 Cunge虽然利用运动波方程的四点带权显式差分格式数值解的一阶截断误差等于扩散波扩散系数这一条件,给出了Muskingum法参数x的物理意义,揭示了Muskingum法演算公式就是扩散波方程具有二阶精度的差分解,但是没有给出Muskingum法演算公式作为扩散波方程式显式差分格式解的稳定性条件。 1978年,Koussis[15]针对常微分方程形式的河段水量平衡方程和Muskingum法槽蓄方程式(1),通过Taylor级数展开,导出了下列偏微分方程: (18) 式中:Q为传播流量;c为波速;x为Muskingum法参数;Δx为河段长。 在式(18)中,若令 (19) 式中D为扩散波的扩散系数,则有 (20) 式(20)即为扩散波方程式。这就表明,Kousis的研究结论是河段水量平衡方程与Muskingum法槽蓄方程,在满足条件式(19)的情况下,就是描写扩散波运动的扩散波方程。考虑到式(17),条件式(19)与式(11)完全相同。 Cunge和Kousis从正与反两种角度证明了只要条件式(11)满足,Muskingum法演算公式就是扩散波方程式的二阶精度数值解,河段水量平衡方程和Muskingum法槽蓄方程描述的就是扩散波运动。 由数值分析理论知,只有具有计算稳定性的差分格式才有意义,否则就会因截断误差在传递过程中的放大或震荡,造成所描写的现象的物理图景不合理的后果。隐式差分格式是无条件稳定的,但显式差分格式却是条件性稳定的。Muskingum法的演算公式作为扩散波方程的显式差分解的稳定性条件是什么呢? 2008年,笔者[16]曾应用Ven Neumamm理论对Muskingum法的数值稳定性进行分析,得到的稳定性条件为 x≤0.5 (21) 联系到曾经对式(11)所作的分析,x≤0.5不仅是Muskingum法物理意义上的要求,而且是数值解稳定性的条件。 a. 如果说St.Venant方程组的问世开创了用水力学理论探索河道洪水波运动的途径,那么Muskingum法的出现便开始了用水文学理论研究河道洪水波运动的途径。经过近一个世纪的发展,不仅找到了这两条途径的共同点,也明确了它们的不同点。适用于运动波和扩散波的洪水演算是它们的共同点,是否适用动力波的洪水演算是它们的不同点。 b. 笔者认为在近百年中,Muskingum法的发展已经历了3个时期,即经验解释时期、特征河长解释时期和水力学解释时期。在经验解释时期,论及的中心议题是槽蓄方程的构建和示储流量的实质。在特征河长解释时期,论及的中心议题是Muskingum法与特征河长的关系,以及用Muskingum法进行洪水演算时初始阶段出现不合理现象的原因。在水力学解释时期,论及的中心议题是Muskingum法的水力学基础和Muskingum法计算结果物理上合理、数值上稳定的条件。Muskingum法的理论和应用价值就是在这样的发展过程中得到了不断的提升。 c. Muskingum法的槽蓄方程,原本是一个经验假设,但在世界上许多河流的洪水演算中取得了令人满意的精度。一个经验性的假设为什么能屡屡得到应验呢?是不是这个假设实质上已是人们不自觉地揭示了洪水波运动的本质了呢?如果是这样,那么这种洪水波该是什么样的洪水波呢?现在水文学家终于交出了一份很好的答卷。这一事件表明,在科学研究中,“经验”不一定永远是经验,有些“经验”,尤其是那些似乎“放之四海而皆准”的经验,终有一天会上升到“理论”的。从这个意义上说,“经验”与“理论”之间并不存在一条不可逾越的鸿沟。在这种由“经验”向“理论”的升华过程中,科学家的正确思维方法、持之以恒的探索精神、百折不挠的学术批判是十分重要的。 d. 重要的科学发现经常是从某种“假设”开始的,但是在当今的教科书中,总是将一些重要的定理和定律整理“提炼”得有条不紊,好像它们生来有之。这样,久而久之,学生们就习惯于 “经验性”的永远是经验性的、“理论性”的永远是理论性的思维方式,而对于在科学探索中发生的实际思维过程却反而不知甚至不能理解。事实上,在科学史上起引领作用的定律曾经就是一种猜想。就是在今天,科学上仍然充满了猜想。没有“猜想”就难以有“创新”。 e. 学习任何知识均应将精力放在正确理解其精神实质上,要牢牢掌握其精髓,而不应采用功利主义的态度,浮在表面就开始做“创新”的美梦。君不见,有文献曾经将计算与实测流量的离差平方和最小作为目标函数,用最优化方法直接率定Muskingum法的演算系数C0、C1和C2,或者再增加一个水量平衡约束,即C0+C1+C2=1来率定C0、C1和C2。更有甚者,竟将计算与实测水位的离差平方和最小作为目标函数来率定C0、C1和C2。所有这些做法,由于不能保证Muskingum法中x的物理意义,故均不能称为对Muskingum法的改进和发展。相反,这是一种将原本物理概念清楚的方法胡乱地变成“黑箱子”方法的典型事例。科学研究的目的是尽可能将“黑箱子”变“灰”、变“白”,而不能将“白箱子”变“灰”、变“黑”。 f. Muskingum法的参数x和特征河长l与弗劳德数存在关系,表明了它们与流态有关。由式(13)和式(14)可知,当流态为F0>2的急变流时,出现了x>0.5和l<0的不合理现象,这是为什么?既然Muskingum法的演算公式是扩散波方程具有二阶精度的四点带权显式差分格式的数值解,为什么只能通过运动波方程才能得到,直接利用差分格式求解扩散波方程却不能得到?笔者认为这些也许是必须进一步深入研究的问题。若通过物理实验方法来揭示Muskingum法的物理基础和适用条件,则将更有意义。 参考文献: [1] VIESSMEN W, KNAPP J W, GARY L L,et al.Introduction to hydrology[M].New York: Harper & Pow, 1977. [2] CHOW V T.Handbook of applied hydrology[M].New York: McGraw-Hill, 1964. [3] LINSLEY R K, KOHLER M A, PAULHUS J L H.Hydrology for engineers[M].3rd ed.New York: McGraw-Hill, 1988. [4] 华东水利学院水文系.水文预报[M].北京:中国工业出版社,1962. [5] 钟乐晖.用数解法推求马斯京根洪水演算法中X和K的数值[J].水利学报,1963(2):43-45.(ZHONG Lehui.The calculation of parametersXandKof Muskingum flood routing method with numerical method[J].Journal of Hydraulic Engineering,1963(2):43-45.(in Chinese) [6] 华东水利学院.中国湿润地区洪水预报方法[M].北京:水利电力出版社, 1978. [7] 芮孝芳.Muskingum法及其分段连续演算的若干理论探讨[J].水科学进展,2002,13(6):682-688.(RUI Xiaofang.Some theoretical studies on the Muskingum method and its successive routing in subreaches[J].Advances in Water Science,2002,13(6):682-688.(in Chinese) [8] KALININ G P,MILYUKOV P I.Approximate computation of unsteady flow[R].Leningrad:Trudy C.I.P.,1958.(in Russian). [9] 芮孝芳.水文学原理[M].北京:高等教育出版社, 2013. [10] 赵人俊.流域汇流计算方法[J].水利学报,1962(2):1-9.(ZHAO Renjun.Watershed concentration calculation method[J].Journal of Hydraulic Engineering,1962(2):1-9.(in Chinese) [11] 赵人俊.流域水文模拟[M].北京:水利电力出版社, 1984. [12] DOOGE J C I.Linear theory of hydrologic systems[M].Washington,D.C.:USDA,1973. [13] CUNGE J A.On the subject of a flood propagation method:Muskingum method[J].Journal of Hydraulic Research,1969, 7(2):1087-1101. [14] 芮孝芳.运动波数值扩散与洪水演算方法[J].水利学报,1987(2):37-43.(RUI Xiaofang.Numerical dispersion of kinematic wave and flood routing method[J].Journal of Hydraulic Engineering,1987(2):37-43.(in Chinese) [15] KOUSSIS A D.Theortical estimations of flood routing parameters[J].Journal of the Hydraulics Division,ASCE,1978, 104(HY1):109-115. [16] RUI Xiaofang,LIU Fanggui,YU Mei.Discussion of Muskingum method parameter X[J].Water Science and Engineering,2008, 1(3):16-23.2.3 连续演算的Muskingum法


3 水力学解释时期
3.1 Dooge的研究
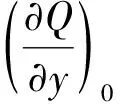
3.2 Cunge的研究
3.3 Koussis的研究
3.4 笔者的研究
4 结论与启示
