某超大直径断面顶管施工引起的地层位移分析①
2014-03-22王剑邓宗伟
王剑,邓宗伟
(湖南城市学院土木工程学院,湖南益阳413000)
随着我国城市人口的不断增加,地下管道的数量也随着增加,顶管法作为一种先进的铺管技术,以开挖量小、对周围环境影响小以及施工速度块等显著优点而被越来越多的应用[1-2]。顶管施工诱发的地层环境损伤问题,即地表变位的预测与控制成为亟待研究和解决的课题。
针对隧道施工引起的地层位移,各国学者进行了大量的研究,常用方法包括Peck公式、解析法、数值分析法等。Peck[3]认为地表沉降曲线呈高斯分布;郭延华等[4]基于南京地铁2#大量的实测数据以及地质条件,采用修正的Peck公式获得良好的预测效果;卢海林等[5]根据地层损失与注浆量的空间分布规律,应用镜像方法,对盾构法隧道推进产生的土体位移与应力进行空间分析,得到隧道周围土体的位移与应力分布;张海波等[6]通过对某地铁隧道盾构施工过程的模拟,分析了盾构推进过程中隧道周围及地表土体的位移和变形以及横断面不同深度上的沉降分布规律。本文基于随机介质理论,依据某超大直径断面顶管隧道现场施工地表沉降监测数据反演地层2个基本计算参数tanβ和ΔA;采用隧道变形均匀收敛模型、非均匀收敛模型以及Peck公式计算地表沉降,分析得到最适用于该隧道地表沉降预测的方法并预测隧道穿越后的累计地表变形和位移,评估隧道施工对民房结构的影响程度。对隧道埋深、开挖断面大小、地层条件和施工条件4个对地表移动和变形的影响因素进行定量分析,为以后类似的工程实践提供理论参考。
1 随机介质基本理论及简化过程
1.1 随机介质理论及简化
随机介质理论将岩土视为一种“随机介质”,隧道开挖对地表影响可等效为构成这一开挖的无限多个微小单元开挖的影响总和。在目前的随机介质理论研究中,一般基于假定隧道产生均匀收敛,以计算地层位移。但是,隧道断面的收敛形式受多种复杂因素(例如地层应力的分布、土体各向异性、施工步骤等)的影响,实际的收敛变形情况并不是严格均匀的。表1为单孔椭圆隧道均匀与非均匀收敛模式的对比示意图。
Verruijt和Booker的研究表明:假定隧道开挖断面发生均匀径向收缩时,计算的地表沉降槽曲线比实测结果要宽,且侧向变形偏大[7];韩煊等[9]将以上不均匀收敛模式引入随机介质理论,通过算例分析,表明该收敛模式比均匀收敛模式计算结果更为精确;伍振志[10]对隧道开挖断面均匀收敛模式及底部土体位移不为0mm的非均匀收敛模式进行了探讨。
本文在前人工作的基础上,根据本工程的地质条件,考虑底部为0 mm的非均匀模式对顶管隧道进行分析与计算。
1.2 Peck经验公式理论
在隧道掘进工程中产生地层损失,不考虑土体排水固结与蠕变的情况下,地层移动是一个随机过程,在隧道掘进过程中地表形成的横向槽为近似正态分布曲线,其预测地表沉降分布公式为:
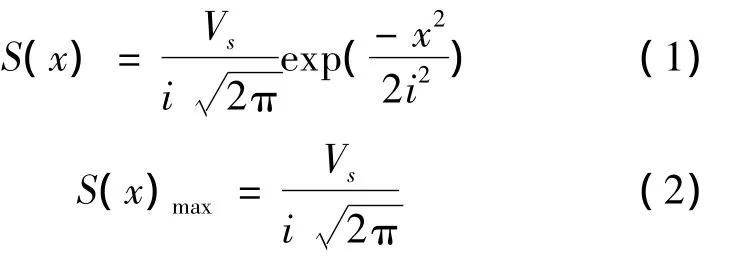
式中:S(x)和S(x)max为距离隧道中心轴为x处地表沉降值及最大值;Vs为隧道单位长度地层损失; i为地表沉降槽宽度系数。
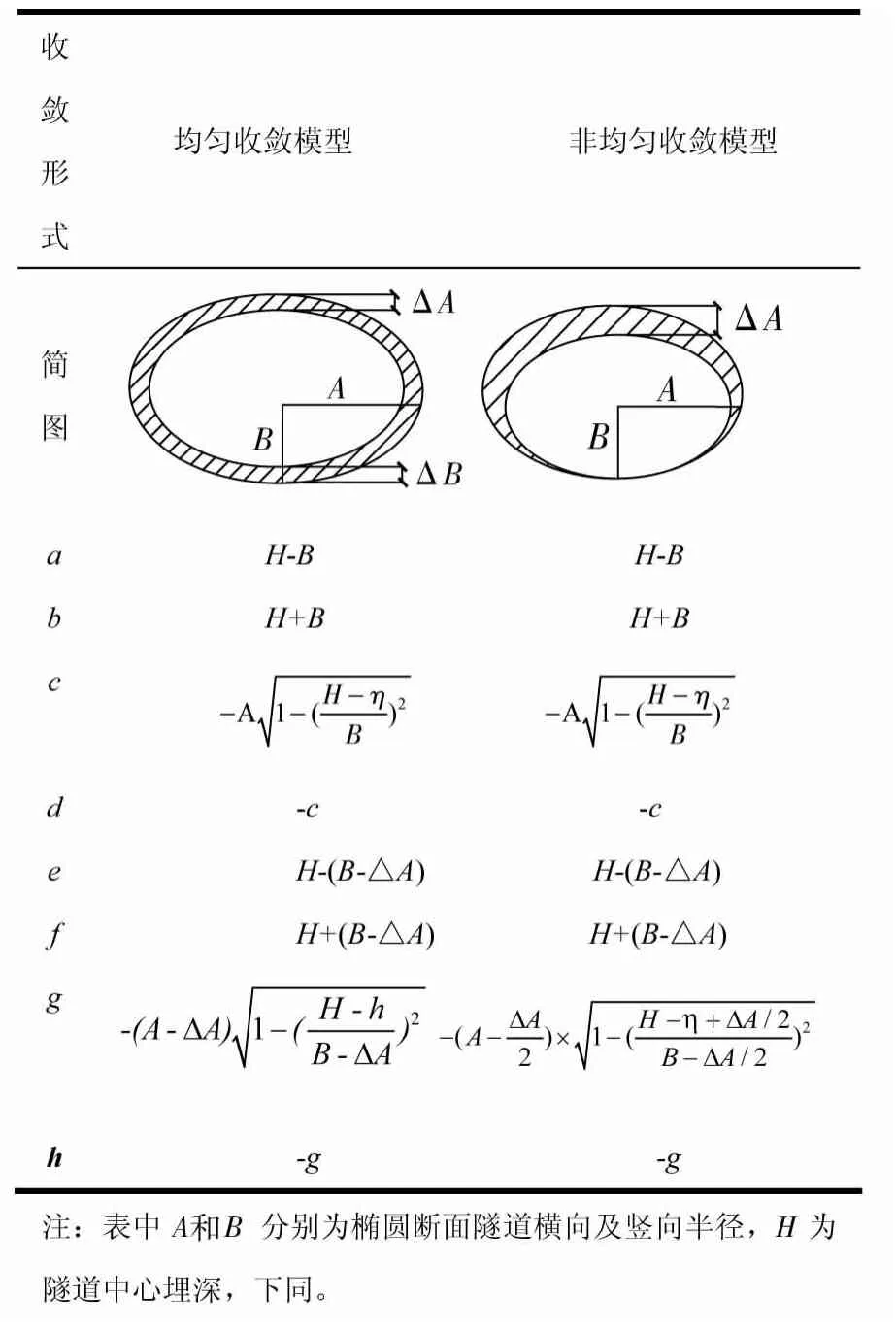
表1 非均匀与均匀收敛模型对比(单孔椭圆截面隧道)Table 1 Comparison of uniform and non-uniform convergence model(single elliptical tunnel)
2 顶管施工监测概况
2.1 工程概况
某超大直径断面顶管水系改造工程,一边为地势低洼垸子,原有建筑基本都为砖混结构,另一边紧靠围山渠,顶管从路正中间穿过,埋深较浅,仅4.9 m,顶管的直径又较大,内径达2.6 m,外径达3.07 m,且穿越的主要土层为素填土,上覆土层浅且开挖面上下土性差别较大,该管道所处位置及各土层分布如图2所示,具体岩层参数如表2所示。
周边民房基础及结构刚度差,有些老民房的承重墙和横梁在顶管穿越前已出现轻微结构损伤现象。本次穿越工程难度大、风险高且缺乏可供借鉴的工程实例,拟将大部被征用民房地段作为“试验段”,对隧道施工引起的地表沉降监测数据进行计算分析,预测隧道施工引起的横向地表变形和位移,评估隧道施工对周围环境的影响程度,据以为制定施工地表变位控制措施提供参考借鉴。
2.2 施工监测概况
为得到地面沉降曲线以及顶管施工对地面竖向位移的影响范围,在“试验段”,沿轴线和断面布置了17个地面沉降观测点,各观测点位置如图3所示。
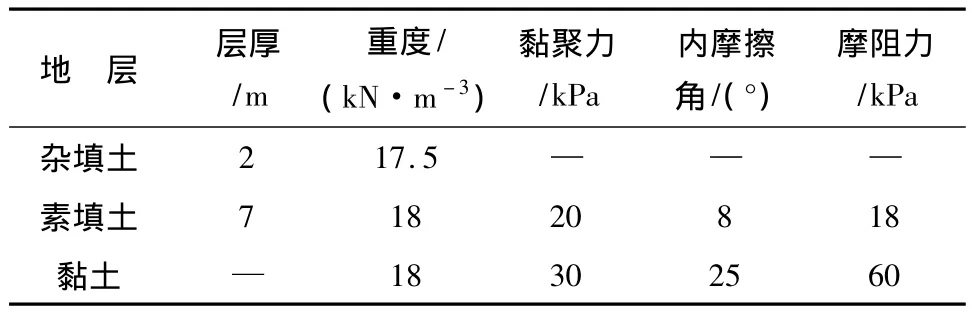
表2 地层物理力学参数Table 2 Physico-mechanical parameters
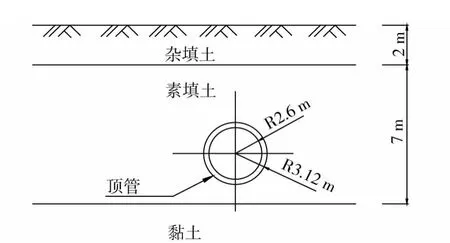
图2 顶管施工断面图Fig.2 Excavation cross section
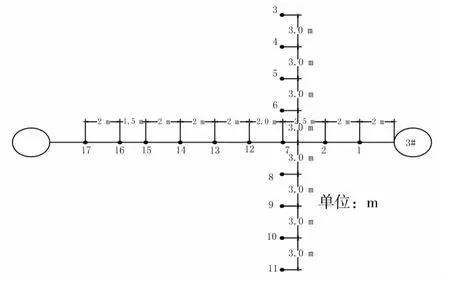
图3 地表沉降观测点平面位置图Fig.3 Layout of ground settlementmonitoring points
3 计算参数反演与变形预测
3.1 计算参数反演
利用前述的Matlab计算程序进行隧道开挖引起的地表移动和变形预计,对于一个具体的隧道工程,在某一段中,隧道的埋深H和开挖半径D都是确定的,但需确定2个基本计算参数:tanβ和ΔA。其中tanβ为开挖主要影响角的正切,取决于隧道开挖所处的地层条件,是地层岩土体特性的综合反映;ΔA为隧道断面半径收敛值,是隧道施工条件的综合反映。由于这2个参数分别是开挖条件和地层条件综合作用的结果,无法用简单的方法加以确定,而其取值正确与否是准确预计地表移动和变形的关键。
综合考虑地质条件影响及监测数据的完整性,本文利用现场“试验段”实测的地表位移值,利用Matlab程序,采用“方向加速法”算法编写计算文件,反分析求算所需的地表移动和变形2个基本计算参数,并且经过后验差检验,检验其拟合精度。拟合得到的△A=33.92 mm,tanβ=0.475,经过后验差检验拟合精度为优级,如表4所示。
3.2 地表变形预测比较分析
为验证本文模型的科学合理性,采用编写的反分析程序对不同的模型参数进行了反演计算,如表5所示,各种收敛模式下的预测值和实测值对比情况如图4所示。由图4可知:底部为0 mm的收敛模式预测精度最高,Peck公式预测精度次之,均匀收敛模式精度最低。
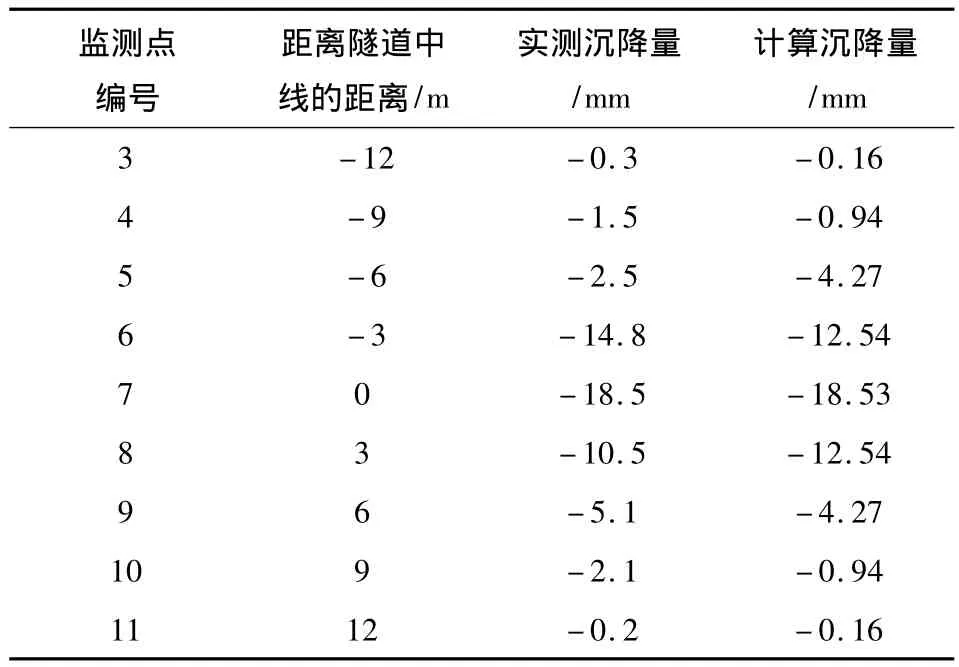
表3 “试验段”断面监测及计算数据Table 3 Monitoring and calculation of data“measurement”section

表4 计算参数计算后验差检验结果Table 4 Results of postcrior-variance-test of

表5 各种收敛模式的反演参数Table 5 Parameters for back-analysis based on three convergencemodes
3.3 累计地表变位预测
采用以上反演参数,对顶管施工导致的累计地表变位进行了预测计算,并将地表变位最大值由表6列出。根据表6中列出的地表变位最大值,以及参照砖混结构建筑物破坏等级[11-12]比较可见:地表曲率过大,达到破坏等级Ⅳ级水平。因此,必须参考该断面,对隧道周围民房较多地段的施工进行参数匹配和必要的保护措施。
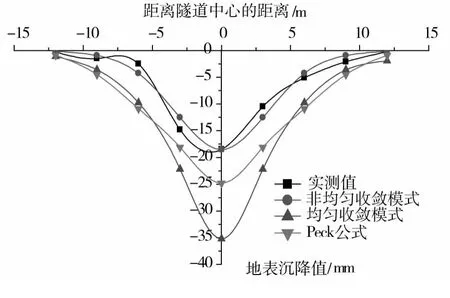
图4 不同收敛模式预测曲线与实测曲线对比图Fig.4 Settlement curve based on three convergencemodes

表6 地表变位最大值Table 6 Max deformation of the ground
4 地表变形影响因素的分析
隧道施工引起的地表移动和变形与隧道的影响因素主要有:隧道的埋深H、开挖断面大小(开挖直径D)、开挖后隧道的断面收敛值ΔA和隧道开挖所处的地层条件tanβ。分析隧道开引起的地表移动和变形的影响因素,对于在不同的地质和施工条件下,采取有效的工程措施减少开挖对周围环境的影响具有重要的意义。本文通过采用变化一个参数取值,固定其他3个参数取值的方法,基于本工程具体实践,分别取以下4种情况,如表7所示。

表7 影响因素取值Table 7 The parameters for different excavation conditions
4.1 开挖深度的影响
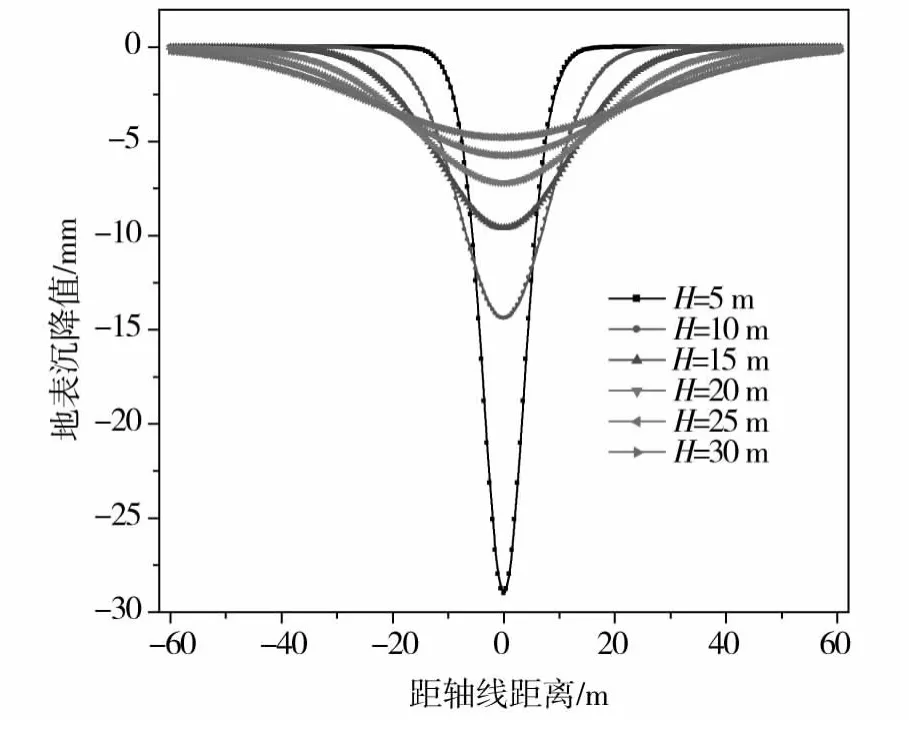
图5 不同开挖深度地表沉降分布Fig.5 Settlement distribution of under different H
由图5可知,在其他条件不变时,随隧道开挖深度增大时,地表最大沉降值减小;图6为计算最大地表沉降值与隧道开挖深度之间的关系曲线,最大沉降值随开挖深度的增加呈对数衰减规律。同时,当隧道埋深增大时,地表的最大水平位移和变形值也都相应减小,因此增大隧道的埋深有助于减少地表位移和变形,对地面设施的保护有利。对于浅埋隧道,更应注意采取工程措施,减少开挖对地表可能造成的不利影响。但随着隧道深度的增大,开挖对地表的影响范围越大,即开挖引起的地表沉降槽的宽度也越大。
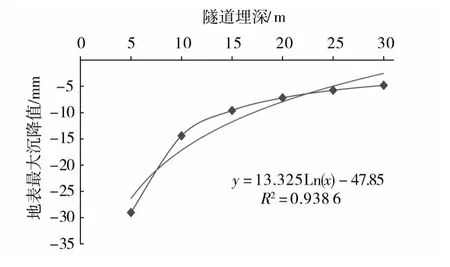
图6 最大沉降值与开挖深度之间的关系Fig.6 Relationship betweenmax settlement and H
4.2 开挖断面大小的影响
由图7和图8表明:在其他条件不变时,地表沉降值、沉降槽的宽度均随隧道开挖直径增大而增大,地表最大沉降值与隧道断面尺寸之间近似呈线性关系。
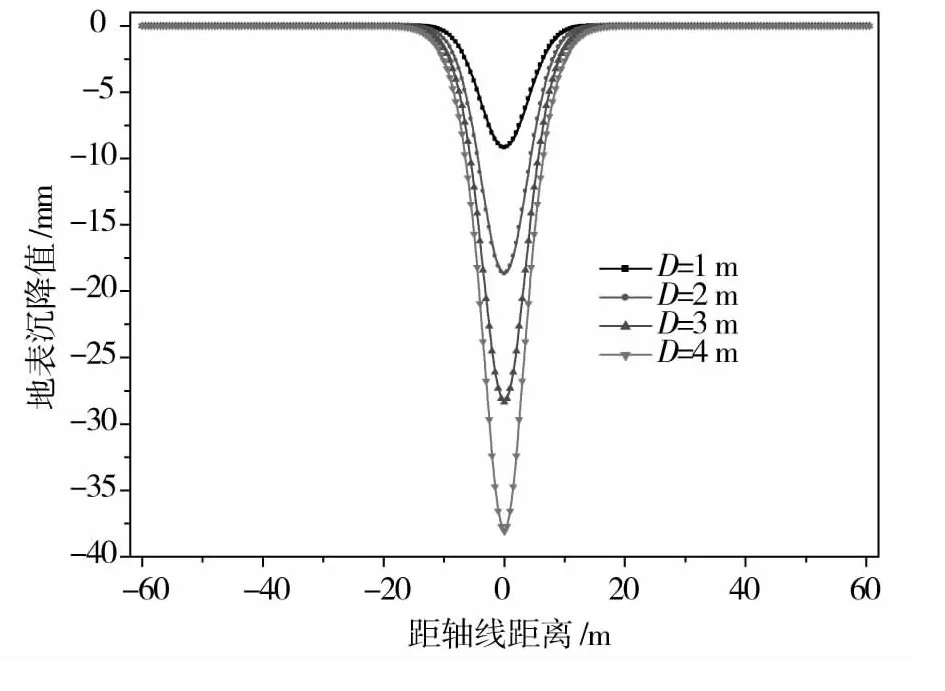
图7 不同开挖直径时地表沉降分布Fig.7 Settlement distribution under different D
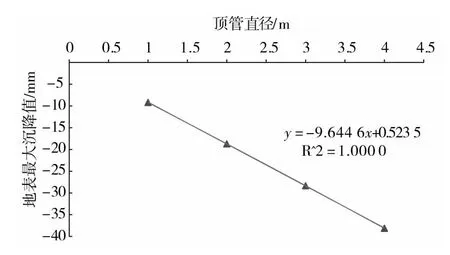
图8 地表沉降值与顶管直径的关系Fig.8 Relationship betweenmax settlement and D
4.3 地层条件的影响
地层条件不仅影响地表移动和变形值,而且直接影响着隧道施工方法的选择。地层条件的不同,在地表移动和变形计算公式中,反映在开挖的主要影响角的不同。由计算表明,在其他条件不变时,地表沉降随tanβ值的增加而增加,而开挖影响范围随tanβ的增大而减小,如图9所示。同时,最大地表沉降值随tanβ的增加而增大,两者之间近似呈线性关系(如图10所示)。
4.4 施工条件的影响
顶管施工的方法很多,有手掘式顶管、泥水盾构式和土压平衡式。不同的施工方法、施工水平对地表移动和变形的综合影响可由隧道开挖半径收敛值ΔA来反映。由图11表明:在其他条件不变时,地表沉降值随ΔA值的增加而增加。图12给出了地表最大沉降值与隧道半径收敛值ΔA之间的关系,可见地表最大沉降值随ΔA的增加而增大,两者近似呈线性关系。
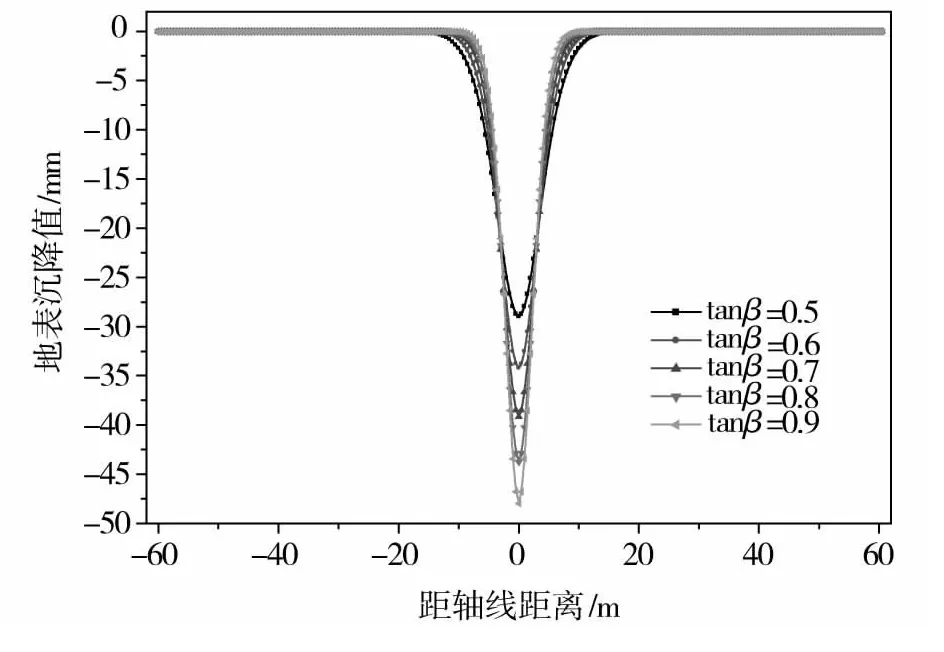
图9 不同tanβ值时的地表沉降分布Fig.9 Settlement distribution under different tanβ
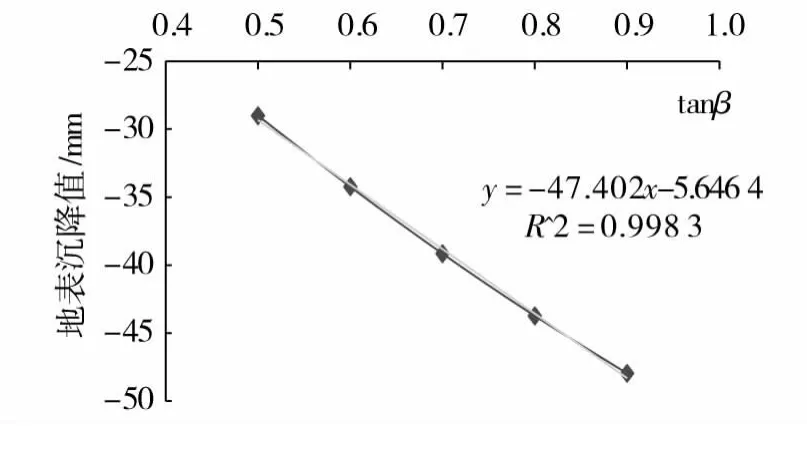
图10 最大地表沉降值与tanβ关系Fig.10 Relationship between max settlement and tanβ
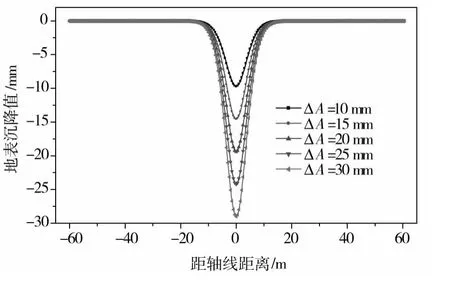
图11 不同△A收敛值时的地表沉降分布Fig.11 Settlement distribution under different△A
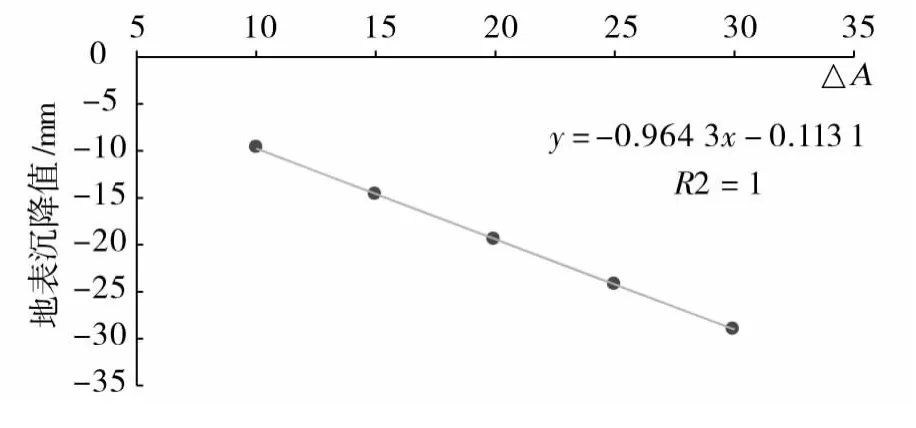
图12 最大地表沉降值与收敛值△A的关系Fig.12 Relationship curve between max settlement and△A
在城市顶管隧道中,为了控制隧道开挖对周围环境的影响,必须根据当地的环境条件、隧道的功能、地层条件合理选择施工方法与工艺,如选择合适的顶管方法,注浆材料等。本文所采用的预测方法,由于方法简单,在矿山与盾构隧道[13]中已得到广泛应用而存在一定的实用价值。
5 结论
(1)根据该工程实践以及监测数据,通过3种收敛模式计算结果的对比分析可知:非均匀收敛模式的预测精度要高于均匀收敛模式及Peck公式,说明了该收敛模式在顶管工程(浅埋、大型)中的科学合理性及应用价值。
(2)本文采用随机介质理论定量分析了影响顶管隧道施工地表变形的因素,计算结果表明:最大沉降值随开挖深度H的增加呈对数衰减规律,地表最大沉降值随隧道直径D、地层影响角正切值tanβ、开挖断面收敛ΔA的增加而呈线性增长。研究表明,对于浅埋软土地层中开挖的超大直径断面,极易产生较大的变形,因此在周围环境复杂时,应采取严格的地表变形控制措施。
[1]余彬泉.顶管施工技术[M].北京:人民交通出版社,1997.YU Binquan.Construction of pipe-jacking[M].Beijing:China Communications Press,1997.
[2]葛春辉.顶管工程设计与施工[M].北京:中国建筑工业出版社,2012.GE Chunhui.Design and construction Pipe jacking engineering[M].Beijing:China Building Industry Press,2012.
[3]Peck R B.Deep excavations and tunneling in soft ground[C]//Proceedings of 7thInternational Conference on Soil Mechanics and Foundation Engineering.Mexico City,1969:275-290.
[4]郭延华,吴龙海.南京地层地铁隧道施工的Peck公式修正[J].河北工程大学学报:自然科学版,2013,1 (30):41-44.GUO Yanhua,WU Longhai.The correction of peck formula in subway tunnel under Nangjing stratum[J].Journal of Hebei University of Engineering:Natural Science E-dition,2013,1(30):41-44.
[5]卢海林,赵志民,方芃,等.盾构法隧道施工引起土体位移与应力的镜像分析方法[J].岩土力学,2007,28 (1):45-50.LU Hailin,ZHAO Zhimin,FANGPeng,etal.Analytical method of image theory used to calculate shield tunneling induced soil displacements and stress[J].Rock and Soil Mechanics,2007,28(1):45-50.
[6]张海波,殷宗泽,朱俊高.地铁隧道盾构法施工过程中地层变位的三维有限元模拟[J].岩石力学与工程学报,2005,5(24):755-760.ZHANG Haibo,YIN Zongze,ZHU Jungao.3d Finite enement simulation on derormation of soilmass during shield tunneling[J].Chinese Journal of Rock Mechanics and Engineering,2005,5(24):755-760.
[7]陈鹏,杨小礼,黄阜.浅埋三孔隧道围岩位移场解析解研究[J].铁道科学与工程学报,2011,01:87-90.CHEN Peng,YANG Xiaoli,HUANG Fu.Analytical solutions of surrounding displacement fields in shallow three tunnels[J].Journal of Railway Science and Engineering,2011(1):87-90.
[8]Lee IM,Nam SW.The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels[J].Tunnelling and Underground Space Technology,2001,16 (1):31-40.
[9]韩煊,李宁.隧道开挖不均匀收敛引起地层位移的预测模型[J].岩土工程学报,2007,29(3):347-352.HAN Xuan,LI Ning.A predicing model for ground movement induced by non-uniform convergence of tunnel[J].Chinese JournalofGeotechnical Engineering,2007,29(3):347-352.
[10]伍振志.基于非均匀收敛模式的隧道地表变形的随机介质预测模型[J].中南大学学报:自然科学版,2010,5(41):2005-2010.WU Zhenzhi.Stochastic medium predicting model of ground movement tunneling based on non-uniform convergencemede[J].Journal of Central South University: Science and Technology,2010,5(41):2005-2010.
[11]张立明.神经网络的模型及其应用[M].上海:复旦大学出版社,1993.ZHANG Liming.Models and applications of artificial neural networks[M].Shanghai:Fudan University Press,1993.
[12]璩继立.盾构施工引起的地面长期沉降研究[D].上海:同济大学,2002.QU Jili.The research on ground subsidence reduced by Shield construction over a long time[D].Shanghai: Tongji University,2002.
[13]吉小明.软土浅埋暗挖隧道开挖面扰动特性及稳定性分析[J].铁道科学与工程学报,2007(4):56-60.JI Xiaoming.Face stability analysis and disturbed behavior of shallow bored tunnel in soils[J].Journal of Railway Science and Engineering,,2007(4):56-60.
[14]伍振志,杨国祥,杨林德,等.基于随机介质理论的大型泥水盾构施工地表变位预测及控制[J].东南大学学报:自然科学版,2009,39(6):1212-1216.WU Zhenzhi,YANG Guoxiang,YANG Linde,et al.Prediction and control of ground deformation and displacement due to large slurry shield tunneling based on stochastic medium theory[J].Journal of Sortheast University:Natural Sicence Edition,2009,39(6):1212-1216.
