基于模糊神经网络的压力传感器零点漂移补偿法
2014-03-21宋志章孙艳梅吴金秋刘文礼
宋志章,孙艳梅,李 会,吴金秋,刘文礼,顾 丁
(齐齐哈尔大学,黑龙江齐齐哈尔 161006)
0 引言
随着集成电路和半导体技术的不断发展,应用半导体材料的压阻效应以扩散工艺制造而成的半导体力敏传感器得到了广泛应用,其中单晶硅压阻式压力传感器以其体积小、灵敏度高、易于小型化和集成化等优点备受青睐。但力敏电阻条的阻值易随温度改变,而且压阻元件的压阻系数具有明显的负温度系数,这导致电阻值与电阻温度系数的离散,使得压阻式压力传感器产生零点漂移[1]。为此,文中将模糊神经网络应用于压阻式压力传感器零点漂移补偿,模糊神经网络是模糊理论与神经网络技术相结合形成的[2],它是正在发展的一门全新的技术,其本质是将神经网络赋予模糊权值[3],模糊神经网络体现了模糊系统和神经网络的互补性,是集语言计算、逻辑推理、分步式处理和非线性映射为一身的系统[4],这些性能恰好满足了压力传感器温度补偿技术的要求。在零点漂移补偿中,模糊神经网络的并行处理能力可加快温度漂移补偿的计算速度和判断速度,它的鲁棒性和容错性可提高抗干扰能力和容错能力,从而提高压力传感器的可靠性和稳定性。
1 压阻式压力传感器
1.1压阻式压力传感器的基本原理
压阻式压力传感器是以硅片作为弹性敏感元件。在该膜片上用集成电路工艺技术制成4个等值薄膜电阻,组成Wheatstone电桥[1],被测压力作用于弹性敏感元件上时,膜片产生与被测压力成正比的微小位移,传感器的电阻值发生变化,Wheatstone电桥失去平衡而产生输出,利用电子线路检测出这一变化,并将其转换成一个对应的标准测量信号。
压阻式压力传感器工作原理图如图1所示。图中阻值相同R1、R2、R3、R4连成Wheatstone电桥的形式,且将R1、R3放在正应力区,R2、R4放在负应力区,当有外界压力作用在膜片上时,R1、R3的阻值将随之增加,R2、R4的阻值将随之减小[5],外加电压VB,Wheatstone电桥电路的输出。

图1 压阻式压力传感器工作原理图
当传感器不受力且电阻值满足:R1R3=R2R4,电路的输出VO=0,当膜片两侧存在压力差时,其将发生形变,使得R1、R3变大,R2、R4变小,Wheatstone电桥失去平衡,产生输出:
(1)

1.2零点漂移
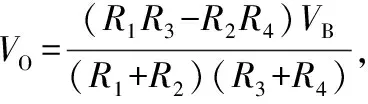
VO=VBP0/Q
(2)
VO与温度密切相关,当温度改变时,VO也会发生改变,这就是零点输出电压的温度漂移,简称为零点漂移。
2 基于模糊神经网络的零点补偿
零点补偿就是用相关算法对从压力传感器采集出的数据进行处理,针对由温度产生的附加误差进行修正[6]。基于模糊神经网络的零点漂移补偿原理如图2所示。

图2 传感器补偿原理图
传感器数学模型为:
Up=f(x,Ut)
式中:x为被测量;Up为压力传感器的输出;Ut为环境参数。
在传感器的输出端串联模糊神经网络补偿环节来进行零点补偿,如图2所示。补偿环节的特性函数为:y=f-1(Up,Ut)=x,其中y是补偿后的输出。很明显,y应该等于被测量x,才能实现零点补偿。但f-1往往很复杂,难于准确求解,而模糊神经网络具有强大的非线性映射能力,可利用模糊神经网络学习并逼近f-1实现压力传感器的零点补偿。
2.1模糊神经网络

式中c和σ分别为隶属函数的中心和宽度[4-9]。
第三层决定了模糊规则的训练速度,第四层是输出层。

图3 模糊神经网络结构图
若用I表示输入信息,O表示输出信息,则每层的输入输出关系为:
第一层:
(3)
第二层:
(4)
第三层:
(5)
第四层:
(6)
式中:ω为第三层到第四层的连接权值。
2.2模糊神经网络的学习算法

高斯函数参数的调整公式为:
式中:η为学习速率;β为动量参数。
根据反向传播算法从性能指针出发来推导模糊多层前馈神经网络的学习算法,得到模糊神经网络各参数的学习规律为:
(7)
σki(t+1)=σiki(t)=η(yd-y)·
(8)
ciki(t+1)=ciki(t)+η(yd-y)·
(9)
模糊神经网络不但在输入输出端等效于具体的模糊系统,而且网络内部与模糊系统的模糊化、模糊推理、解模糊对应,可用模糊系统的概念加以解释,因而是透明的[10-12]。模糊系统的模糊规则以及隶属函数参数的修改在网络中转变为局部节点或权值的确定和调整,学习速度较快。
3 基于模糊神经网络的零点漂移补偿实现步骤
基于模糊神经网络的零点漂移补偿可分为2步:
3.1网络学习
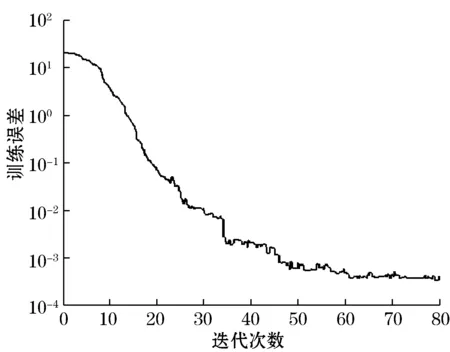
在传感器的测量范围内随机抽取n个u=[u1,u2,…un]以及相应输出值v=[v1,v2,…vn],按照式(3)-式(6)对vi进行模糊量化。随机产生一组网络初始权值,以每个vi作为模糊神经网络的输入值Ii,按照式(6)计算出网络的实际输出yi;再以ui作为模糊神经网络的期望输出ydi,按照式(7)-式(9)训练模糊神经网络的权值,直到|yi-ydi| 3.2误差补偿 实际测量的物理量u,经过传感器转换后输出为v=f(u),再经过模糊神经网络泛化后,由式(6)计算出实际输出,实现传感器非线性误差补偿。 本文选取PT14型压力传感器为研究对象,其量程为:p0~p0+10 kPa(P0为标准大气压);精度:1.0%;工作温度:-10~85 ℃;补偿温度:0~70 ℃。零点输出如表1所示。其中UP为压力传感器的输出,Ut为其工作温度。 表1 传感器零点输出 神经网络输入层为两个节点,分别对应UP和Ut的标准化后的值,输出层为一个节点即修正后的传感器输出。根据PT14型压力传感器的理想标定值,网络的期望响应为28.2,目标误差为10-3,在模糊神经网络学习的过程即各层神经元节点间的连接权值的优化过程,它们共同作用,最后达到了零点补偿的目的,图4为网络迭代训练曲线,训练45次即可使误差达到理想值0.001 243,图5为模糊数据网络的补偿结果,经计算,采用模糊神经网络得到的曲线很好,其相对误差为0.27%,成功地减小了压力传感器的输出误差,将传感器的精度有中低级提高到了中高级。可见,算法在运算速度上也比一般网络要快得多,且精度更高,补偿的效果更好。 图4 网络迭代训练曲线 图5 网络补偿结果 温度对压阻式压力传感器的零点漂移影响很大,而且呈现非线性特征。针对该问题,文中提出了模糊神经网络的零点补偿方法,通过对压力传感器的输出与期望输出误差的比较,反复修正各层神经元节点间的连接权值,直到满足误差要求为止。仿真结果证明,模糊神经网络可有效补偿压阻式压力传感器的零点漂移,通过这种神经网络模型,可得到精度较高的仿真模型,整个过程稳定,收敛速度较快。 参考文献: [1]孟立凡,郑宾.传感器原理及技术.北京:国防工业出版社,2005:120-121. [2]刘清.传感器模糊神经网络非线性误差补偿的研究.自动化仪表,2006,27(3):11-17. [3]张宏韬,姜辉,杨建国.模糊神经网络理论在数控机床热误差补偿建模中的应用.上海交通大学学报,2009,43(12):1950-11961. [4]李冠中,王雷.基于模糊神经网络的MEMS陀螺温度漂移建模.厦门大学学报(自然科学版),2008,47(4):511-513. [5]刘宇,孙燕斌,江永清.基于光纤陀螺的方位传感测井仪误差补偿算法.半导体光电,2009,30(1):138-141. [6]温晓君.基于模糊神经网络的传感器可信度实时获取.电子器件,2007,303(3):954-957. [7]张洵,靳东明,刘华瑞,等.基于模糊神经网络的智能巨磁电阻传感器设计.计算机工程与设计,2007,28 (04):895-897. [8]刘宜平,沈毅,刘志言.一种基于模糊神经网络的故障分类器及其在多传感器故障诊断中的应用.传感技术学报,2000(1):38-43. [9]刘宇,孙燕斌,江永清.基于光纤陀螺的方位传感测井仪误差补偿算法.半导体光电,2009,30(1):138-141. [10]温淑焕.机器人模糊神经网络阻抗控制.系统仿真学报,2004,16(11):2614-2617. [11]De BRUYKER D,Puers R.Thermostatic control for temperature compensation of a silicon pressure sensor.Sensors and Actuators A:Physical,2000,82(1):120-127. [12]郭颖,周王民,马戎,等.基于神经网络的光纤光栅电流传感器的温度补偿,传感技术学报,2008,21(9):1528-1531.4 仿真结果与结果分析


5 结论
