微加速度计在高冲击下的断裂失效分析

陈学强，闫明明，徐晓辉，郭　涛,石云波

(1．仪器科学与动态测试教育部重点实验室，中北大学，山西太原　030051；2．电子测试技术国家重点实验室，中北大学，山西太原　030051；3．洛阳理工学院工程训练中心，河南洛阳　471023)

0　引言

近年来，MEMS技术不断发展，因其具有可大批量生产、成本低、功耗小和集成化等特点，其应用越来越多。其中，硅微加速度计广泛应用于工业、航天和国防技术等领域，如飞机、船舶用的稳定和控制系统、机器状态检测系统等。而在制造、测试以及运输过程中，硅微加速度计极易受到冲击载荷的影响，尤其是在一些特殊应用中，冲击载荷是很常见的，这就对MEMS器件的可靠性提出了更高的要求。为了保证MEMS器件成功应用，必须确保其能够承受一定强度的冲击[1]，在实验中采用Hopkinson杆或空气炮等设备对硅微加速度计进行冲击试验。

文中采用仿真的方法，利用动态加速度冲击仿真方法和三向正弦应力冲击仿真方法来检验微加速度计的抗过载性能，由此得到该微加速度计断裂失效时的冲击加速度。同时对冲击试验下微加速度传感器结构的抗冲击性能进行分析，为微加速度计可靠性分析提供理论依据[2]。

1　微加速度计的敏感元件结构

高量程压阻式加速度传感器敏感元件的整体结构如图1所示，其量程为150 000g，压敏电阻对称分布在四根梁的端部，可以很好地降低横向灵敏度。

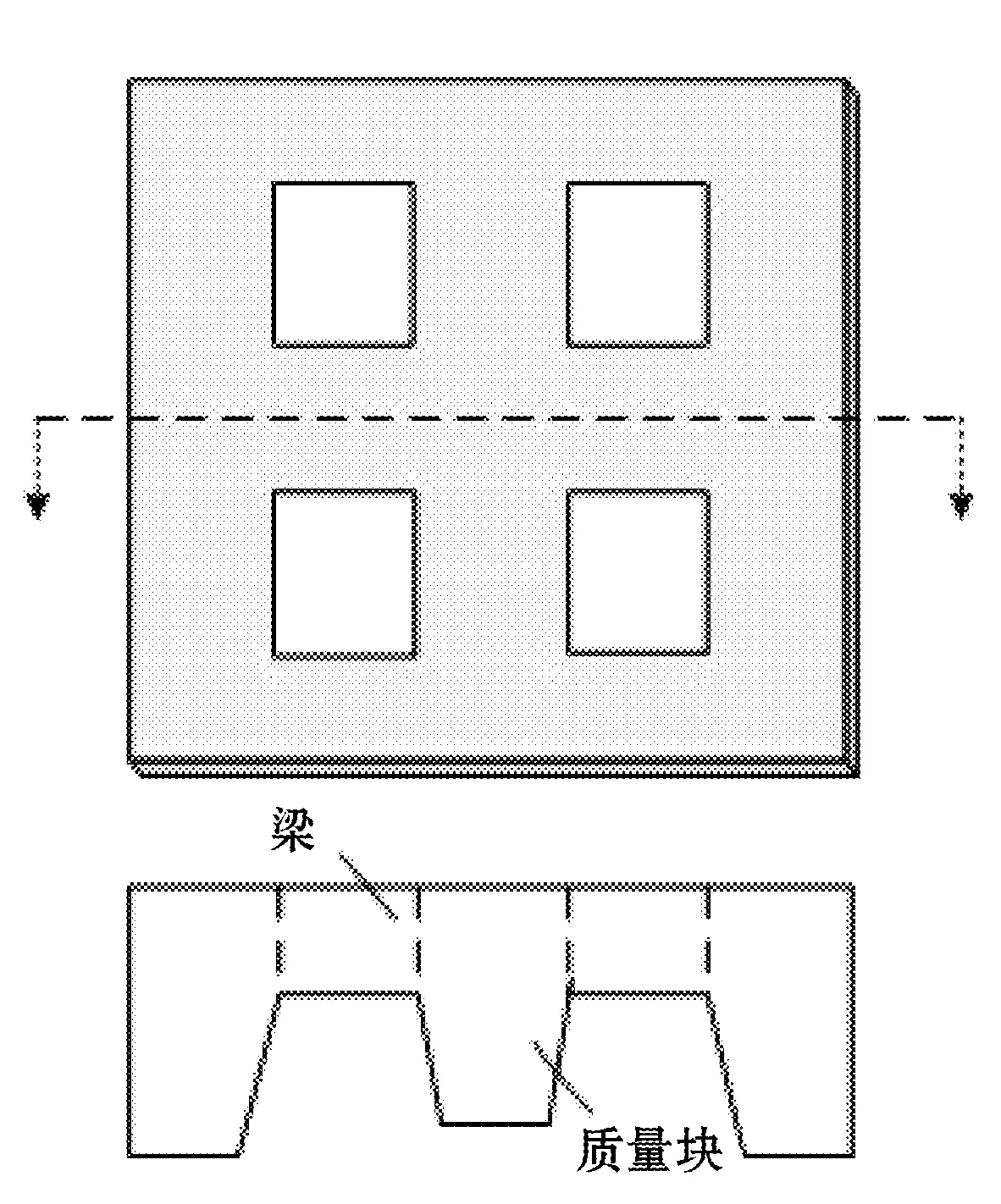
图1　微加速度计结构图

2　微加速度计静态分析

根据该微加速度计结构，对梁结构进行拟静态分析如下：

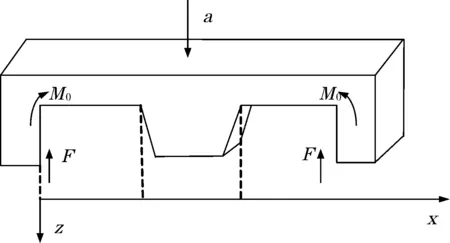
图2　微加速度计受力分析图

为了简化计算，将梁结构等效为简支梁结构，由于结构在xoy面内完全对称，将结构简化为如图2所示双端全固支梁岛结构。由梁的挠曲线微分方程可得梁的弯矩方程为：

(1)

式中：M0为梁边缘的约束弯矩；F为两端固支面的支座反力；l为梁的总长；0≤x≤l．

当加速度a作用于质量块上时，由梁的边界条件可得：

(2)

式中：m1为单边梁的质量；m2为质量块的质量。

梁的弯曲方程为：

(3)

因此，梁截面上的最大弯曲正应力为：

被害人陈述作为证明案件事实的直接证据，往往能充分全面的反映相关的案件情况。从我国目前的办案水平来看，取证的技术手段落后、缺乏必要的设备与经费，[4]所以司法机关对于被害人陈述这一直接言词证据往往格外重视，往往对其进行充分的发掘与利用。也正是因为如此，若被害人故意做出虚假陈述则会产生巨大的危害。一方面，可能会在一定程度上造成对相关的犯罪嫌疑人、被告人的轻罪重罚或无罪乱罚现象。比如，2006年在黑龙江省绥化市就发生过一强奸案件的被害人胡乱陈述，公安机关轻信被害人的虚假陈述，结果导致其无辜邻居史某被刑讯逼供含冤入狱5年的冤案。另一方面，也有可能出现重罪轻判，有罪不判的情况。

(4)

式中b和h分别为梁截面的宽度和厚度。

因该梁结构在xoy面内完全对称，可以认为该结构梁的刚度相对增加1倍，梁上的应力相应减小为一半，即

(5)

由于硅的脆性材料特性，在受到冲击后，硅梁几乎不能承受塑性变形，因此当梁上的最大弯曲应力超过其许用应力时，梁将会断裂。根据第一强度理论，此冲击加速度可以由式(6)得到：

(6)

即

(7)

一般认为单晶硅的断裂应力为1～20 GPa，安全系数选为6，因此这里取单晶硅的许用应力为[σ]=20 GPa/6≈340 MPa．代入式(7)可知，梁宽为1 050 μm的微加速度计结构可以承受的最大加速度为2．69×105g．

3　微加速度计的冲击仿真

对微加速度计进行冲击仿真，微加速度计各参数设置见表1、表2。

3．1动态加速度冲击仿真分析

在传感器敏感元件正常工作方向上(y轴方向)，通过以不同的时间增长率对微加速度计施加同一冲击加速度来进行动态仿真分析。通过仿真得到了敏感结构单元在4 ms时间内加载到25×105g冲击加速度下工作方向即y轴的应力分布云图如图3所示。

表1　微加速度计基本参数　μm

表2　材料属性

图3　结构应力分布图

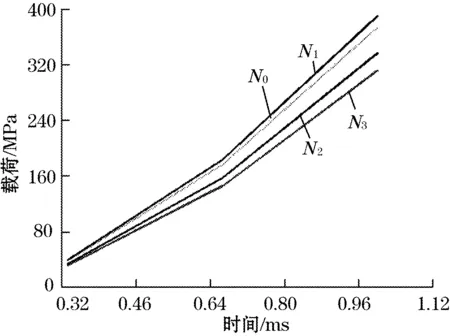
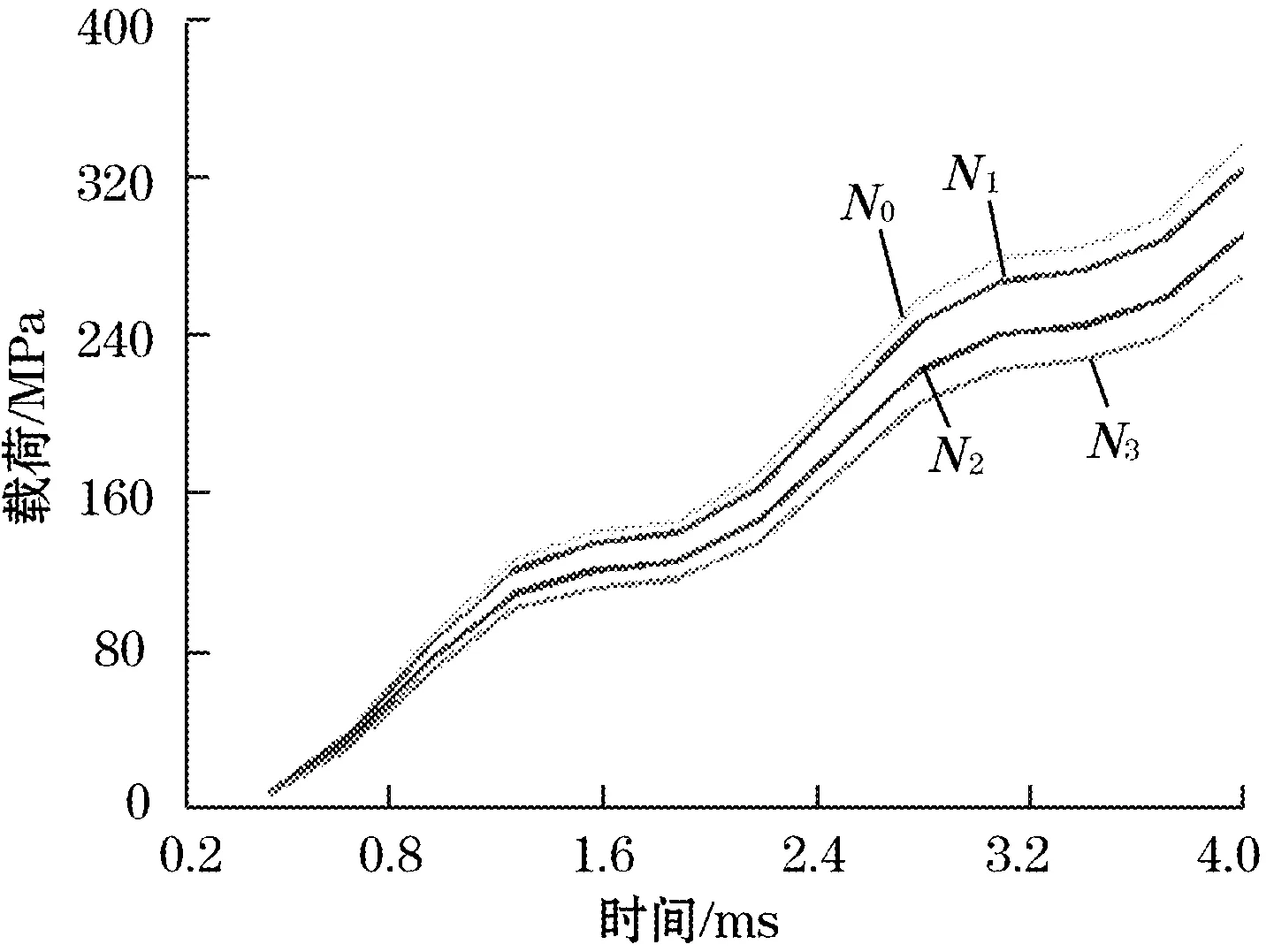
从图3可以看出，由于应力集中，梁的两端比梁的其他地方更早达到最大应力值，当应力值过大将会发生梁的断裂。针对实际使用环境中不同速率的瞬态冲击加速度，仿真时，分别以在1 ms、2 ms、3 ms、4 ms时间段对微加速度计施加从0增加至2.5×104g的冲击加速度，仿真结果如图4所示。其中N0、N1、N2、N3分别表示距离拐点位置的4个节点，如图5所示。

分析图4中节点应力曲线，能够发现在N0处总是比其他节点更早产生最大应力，由此判断梁先从其根部开始发生断裂。由图3可以看出，梁的两端均有应力集中的现象。为了分析梁的哪端先达到最大应力，各取梁两端的两个应力最大值点的应力变化情况绘制在图6中，其中SEQV_2、SEQV_3为固定端节点，SEQV_4、SEQV_5为质量块端节点，从图6可以看到SEQV_2、SEQV_3应力值要大于SEQV_4、SEQV_5，而且产生超过许用应力的时间也早于SEQV_4、SEQV_5，由此可得出该微加速度计结构的多数断裂会发生在固定端的根部，而不是质量块端的根部。

(a)

(b)

(c)

(d)

图5　梁上节点位置分布图

图6　固定端和质量块端应力值

3.2正弦应力冲击仿真分析

由于微加速度计在实际过程中有可能受到来自不同方向的冲击，为了更好地模拟实际的冲击环境[4]，对微加速度计进行不同方向的冲击仿真。

仿真时，以正弦变化的冲击力代替冲击加速度进行仿真试验。分别对微加速度计施加x轴、y轴、z轴相同的正弦变化的应力，应力分布图如图7所示。

(a)x轴

(b)y轴

(c)z轴

其中，对微加速度计进行3个方向的冲击仿真的频率相同，冲击力幅值为5 kN，实际冲击物为20 g，则冲击力等效的加速度约为2.5×105g．从图中可以看出，3个不同方向的同一冲击力下，微加速度计受力最大值处仍为固定端处的梁根部，但工作方向的冲击力对微加速度计产生的应力很大，最大值处为431 MPa，远超过硅的许用应力值，而非工作方向x、z轴上的冲击对微加速度计梁所受的应力大大减小，最大值仅为81 MPa，远小于硅的许用应力。x、z轴方向的力会使微加速度计质量块左端的梁产生正向变形，右端的梁产生负向变形，由此判断，在两位移中心处即质量块端处的梁根部易受剪切应力影响，使得该处发生断裂。

与3．1比较，y轴方向同一加速度下，正弦变化的力提前使梁达到并超过许用应力，加剧了梁的断裂。由此可见，重复性冲击使得微加速度计破坏更严重。再次仿真得出，在正弦冲击下，微加速度计在工作方向上能够承受的最大冲击力为4．1 kN．

从上述仿真实验中可看出，当冲击加速度达到2.5×105g时，微加速度计梁上应力就可能超过340 MPa，会发生断裂，但是理论计算的结果要大于这个值，这是因为以上分析实际上采用的都是静态的方法[5]，而实际仿真时采用动态应力分析的方法计算和分析梁的受力，所以会产生仿真和实际计算结果之间的误差。

4　结论

通过理论分析硅微加速度计在冲击环境下的受力情况，得出微加速度计能承受的最大冲击加速度为2．69×105g．利用动态仿真方法分析了微加速度计结构在冲击载荷下的失效情况，发现瞬时的高冲击能够加速梁的应力集中[6]，并导致梁的断裂，最终得出在4 ms内施加2.5×105g的冲击加速度会使得微加速度计断裂失效的结果；并得出该微加速度计结构的多数断裂会发生在固定端的根部，而不是质量块端的根部；对微加速度计施加3个不同方向正弦变化的冲击加速度，微加速度计在工作方向上能够承受的最大冲击力为4．1 kN；分析得出x、z轴方向正弦变化的力会使微加速度计质量块端处的梁根部易受剪切应力影响，使得该处发生断裂。

参考文献：

[1]唐军，赵锐．冲击环境下MEMS大量程加速度传感器结构的失效分析．传感技术学报，2012，25 (4)：483-486．

[2]祁晓瑾．MEMS高g值加速度传感器研究：[学位论文]．太原：中北大学，2007．

[3]ZHAO Y P，YU T X．Failure modes of MEMS and micro-scale adhesive contact theory．International Journal of Nonlinear Sciences and Numerical Simulation，2000( 1)：361-372．

[4]董明，惠春，徐爱兰．基于Ansys的压电式四臂加速度计模拟分析．传感技术学报，2006，19(3)：637-641．

[5]WANG A W，TIAN W Y．Twin-characteris tic- parameter solution of axisymmetric dynamic plastic buckling for cylindrical shells under axial compression waves．International Journal of Solids and Structures．2003，40：3157-3175．

[6]黎渊．三轴高g加速度计的测试理论与实验研究：[学位论文]．湖北：国防科技大学，2008．